此系列属于胡寿松《自动控制原理题海与考研指导》(第三版)习题精选,仅包含部分经典习题,需要完整版习题答案请自行查找,本系列属于知识点巩固部分,搭配如下几个系列进行学习,可用于期末考试和考研复习。
自动控制原理(第七版)知识提炼
自动控制原理(第七版)课后习题精选
自动控制原理(第七版)附录MATLAB基础
第七章:线性离散系统的分析与校正
Example 7.21
已知系统结构图如下图所示,欲使系统具有 ν = 2 nu=2 ν=2,并在有限拍结束过渡过程,求校正装置形式。
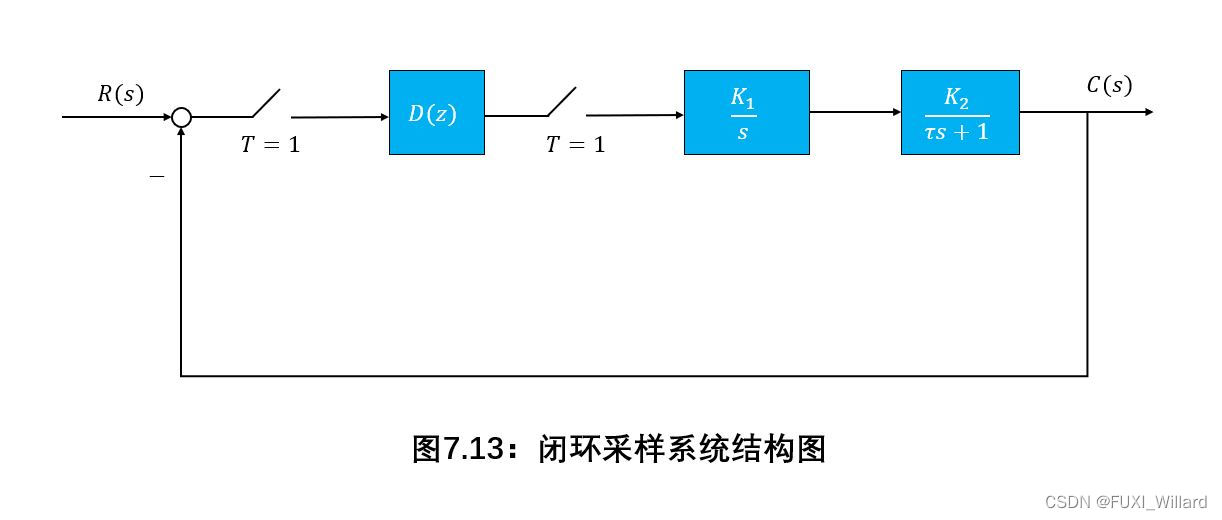
解:
待校正系统开环脉冲传递函数为:
G
(
z
)
=
Z
[
K
1
K
2
s
(
τ
s
+
1
)
]
=
K
1
K
2
Z
[
1
τ
s
(
s
+
1
τ
)
]
=
K
1
K
2
Z
[
1
s
−
1
s
+
1
τ
]
=
K
1
K
2
(
1
−
e
−
1
τ
)
z
(
z
−
1
)
(
z
−
e
−
1
τ
)
G(z)=Zleft[frac{K_1K_2}{s(tau{s}+1)}right]=K_1K_2Zleft[frac{displaystylefrac{1}{tau}}{sleft(s+displaystylefrac{1}{tau}right)}right]=K_1K_2Zleft[frac{1}{s}-frac{1}{s+displaystylefrac{1}{tau}}right]=frac{K_1K_2(1-{rm e}^{-frac{1}{tau}})z}{(z-1)(z-{rm e}^{-frac{1}{tau}})}
G(z)=Z[s(τs+1)K1K2]=K1K2Z⎣
⎡s(s+τ1)τ1⎦
⎤=K1K2Z⎣
⎡s1−s+τ11⎦
⎤=(z−1)(z−e−τ1)K1K2(1−e−τ1)z
因为期望系统为Ⅱ型系统,则开环脉冲传递函数应有两个
z
=
1
z=1
z=1的极点,可见校正装置必有一个
z
=
1
z=1
z=1的极点.
针对单位斜坡输入设计最少拍系统,闭环误差脉冲传递函数为:
Φ
e
(
z
)
=
(
1
−
z
−
1
)
2
=
(
z
−
1
)
2
z
2
Phi_e(z)=(1-z^{-1})^2=frac{(z-1)^2}{z^2}
Φe(z)=(1−z−1)2=z2(z−1)2
校正装置为:
D
(
z
)
=
1
−
Φ
e
(
z
)
G
(
z
)
Φ
e
(
z
)
=
(
z
−
e
−
1
τ
)
(
2
z
−
1
)
K
1
K
2
(
1
−
e
−
1
τ
)
z
(
z
−
1
)
D(z)=frac{1-Phi_e(z)}{G(z)Phi_e(z)}=frac{(z-{rm e}^{-frac{1}{tau}})(2z-1)}{K_1K_2(1-{rm e}^{-frac{1}{tau}})z(z-1)}
D(z)=G(z)Φe(z)1−Φe(z)=K1K2(1−e−τ1)z(z−1)(z−e−τ1)(2z−1)
则闭环脉冲传递函数为:
Φ
(
z
)
=
2
z
−
1
−
z
−
2
=
2
z
−
1
z
2
Phi(z)=2z^{-1}-z^{-2}=frac{2z-1}{z^2}
Φ(z)=2z−1−z−2=z22z−1
其中,系数
K
1
、
K
2
K_1、K_2
K1、K2不影响系统稳定性.
【系统单位斜坡响应曲线】
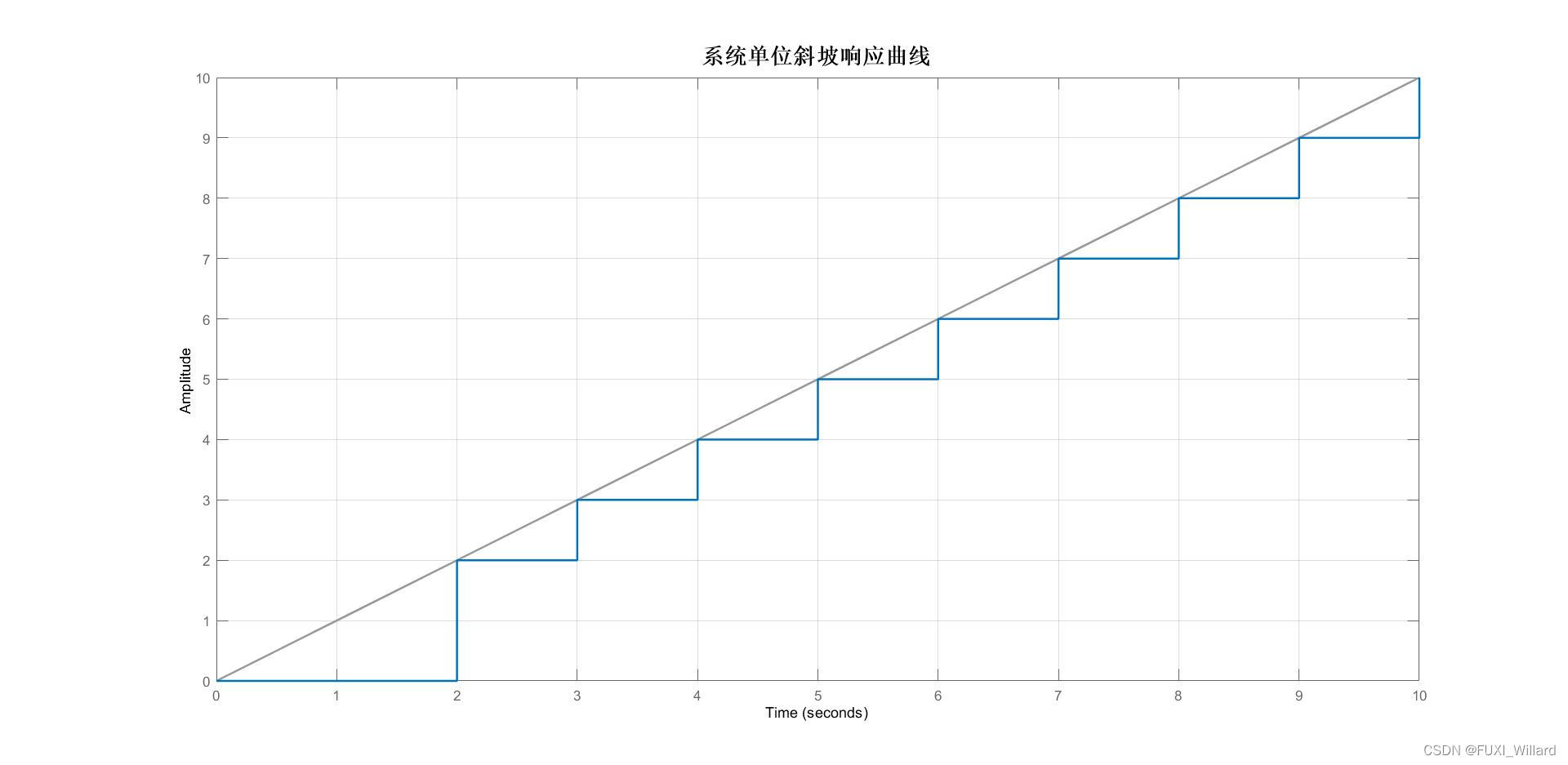
Example 7.22
采样系统的结构图如下图所示,根据无稳态误差和有限拍结束过渡过程的要求,设计数字校正器,并画出输出特性,其中: G 0 ( s ) = 10 s ( 0.1 s + 1 ) ( 0.05 s + 1 ) , T = 0.2 , r ( t ) = 1 ( t ) G_0(s)=displaystylefrac{10}{s(0.1s+1)(0.05s+1)},T=0.2,r(t)=1(t) G0(s)=s(0.1s+1)(0.05s+1)10,T=0.2,r(t)=1(t)。
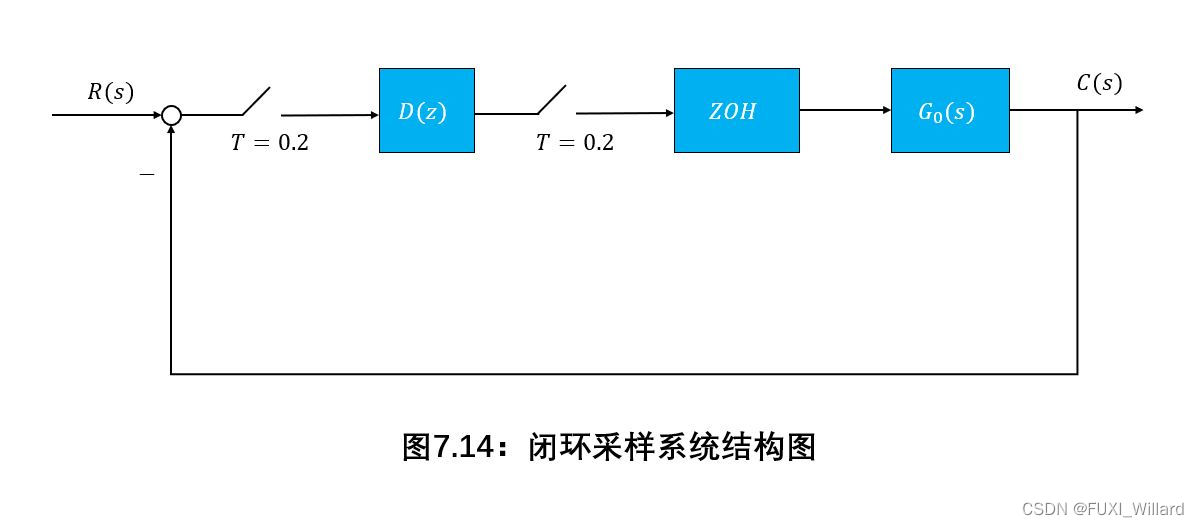
解:
待校正系统开环脉冲传递函数为:
G
(
z
)
=
Z
[
10
(
1
−
e
−
T
s
)
s
2
(
0.1
s
+
1
)
(
0.05
s
+
1
)
]
=
z
−
1
20
z
[
40
z
(
z
−
1
)
2
−
30
z
z
−
1
+
40
z
z
−
e
−
2
−
10
z
z
−
e
−
4
]
=
0.7615
z
2
+
0.8964
z
+
0.0397
(
z
−
1
)
(
z
−
0.1353
)
(
z
−
0.0183
)
begin{aligned} G(z)&=Zleft[displaystylefrac{10(1-{rm e}^{-Ts})}{s^2(0.1s+1)(0.05s+1)}right]=frac{z-1}{20z}left[frac{40z}{(z-1)^2}-frac{30z}{z-1}+frac{40z}{z-{rm e}^{-2}}-frac{10z}{z-{rm e}^{-4}}right]\\ &=frac{0.7615z^2+0.8964z+0.0397}{(z-1)(z-0.1353)(z-0.0183)} end{aligned}
G(z)=Z[s2(0.1s+1)(0.05s+1)10(1−e−Ts)]=20zz−1[(z−1)240z−z−130z+z−e−240z−z−e−410z]=(z−1)(z−0.1353)(z−0.0183)0.7615z2+0.8964z+0.0397
系统为Ⅰ型系统,在单位阶跃输入时,不存在稳态误差.
对单位阶跃输入设计最少拍系统,闭环误差脉冲传递函数为:
Φ
e
(
z
)
=
1
−
z
−
1
Phi_e(z)=1-z^{-1}
Φe(z)=1−z−1
校正装置为:
D
(
z
)
=
1
−
Φ
e
(
z
)
G
(
z
)
Φ
e
(
z
)
=
(
z
−
0.1353
)
(
z
−
0.0183
)
0.7615
z
2
+
0.8964
z
+
0.0397
D(z)=frac{1-Phi_e(z)}{G(z)Phi_e(z)}=frac{(z-0.1353)(z-0.0183)}{0.7615z^2+0.8964z+0.0397}
D(z)=G(z)Φe(z)1−Φe(z)=0.7615z2+0.8964z+0.0397(z−0.1353)(z−0.0183)
则闭环脉冲传递函数为:
Φ
(
z
)
=
z
−
1
Phi(z)=z^{-1}
Φ(z)=z−1
【系统单位阶跃响应曲线】
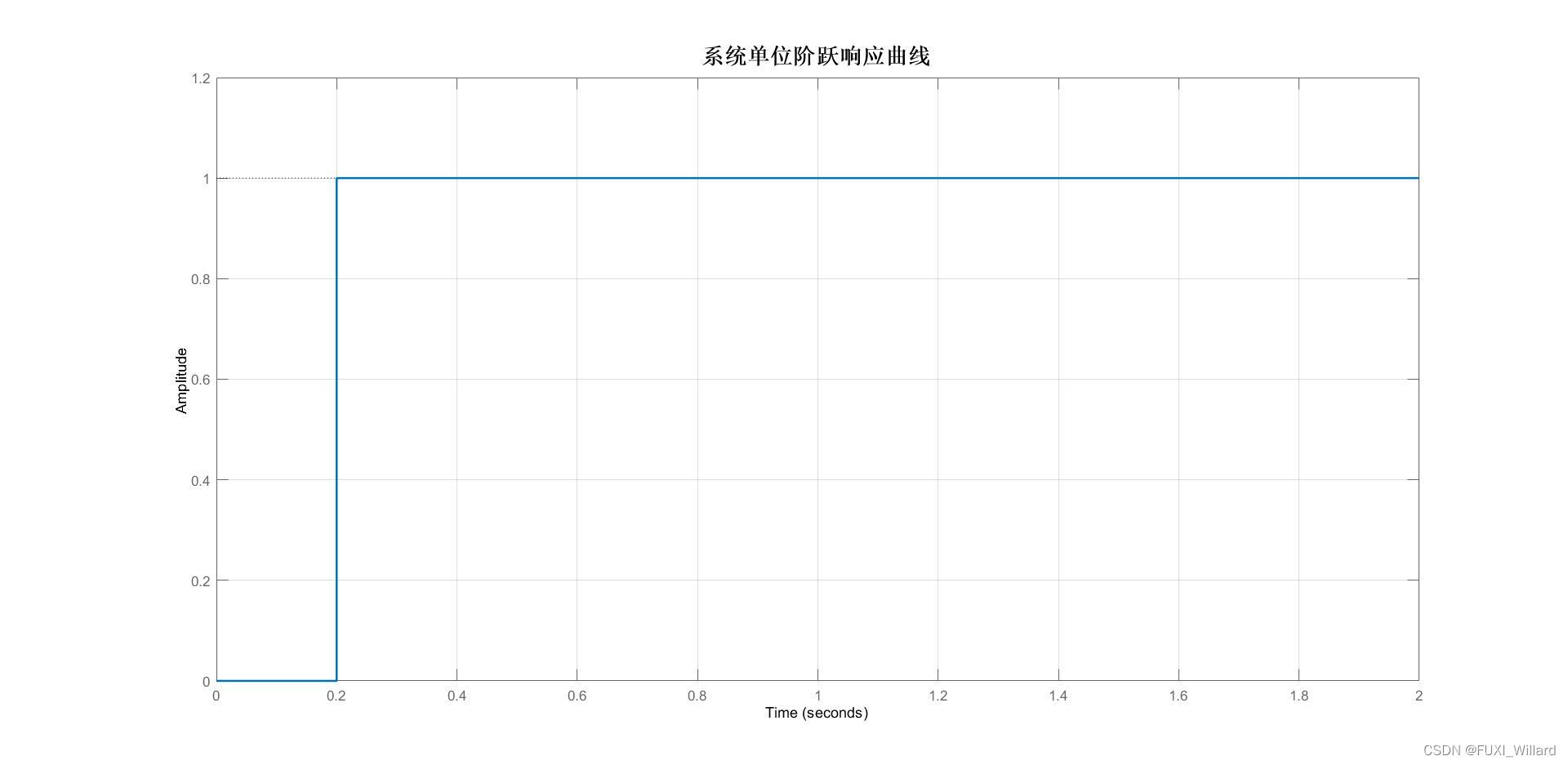
Example 7.23
用
z
z
z变换法求解差分方程:
c
∗
(
t
+
2
T
)
−
6
c
∗
(
t
+
T
)
+
8
c
∗
(
t
)
=
r
∗
(
t
)
,
c
∗
(
0
)
=
0
,
c
∗
(
1
)
=
0
,
r
(
t
)
=
δ
(
t
)
c^*(t+2T)-6c^*(t+T)+8c^*(t)=r^*(t),c^*(0)=0,c^*(1)=0,r(t)=delta(t)
c∗(t+2T)−6c∗(t+T)+8c∗(t)=r∗(t),c∗(0)=0,c∗(1)=0,r(t)=δ(t)
T
T
T为采样周期。要求结果以
c
(
n
T
)
c(nT)
c(nT)表示。
解:
因为:
Z
[
c
(
k
+
2
)
]
=
z
2
C
(
z
)
−
z
2
c
(
0
)
−
z
c
(
1
)
=
z
2
C
(
z
)
Z
[
6
c
(
k
+
1
)
]
=
6
z
C
(
z
)
−
6
z
c
(
0
)
=
6
z
C
(
z
)
R
(
z
)
=
1
begin{aligned} &Z[c(k+2)]=z^2C(z)-z^2c(0)-zc(1)=z^2C(z)\\ &Z[6c(k+1)]=6zC(z)-6zc(0)=6zC(z)\\ &R(z)=1 end{aligned}
Z[c(k+2)]=z2C(z)−z2c(0)−zc(1)=z2C(z)Z[6c(k+1)]=6zC(z)−6zc(0)=6zC(z)R(z)=1
原方程化为:
z
2
C
(
z
)
−
6
z
C
(
z
)
+
8
C
(
z
)
=
1
⇒
C
(
z
)
=
1
(
z
−
2
)
(
z
−
4
)
z^2C(z)-6zC(z)+8C(z)=1Rightarrow{C(z)}=frac{1}{(z-2)(z-4)}
z2C(z)−6zC(z)+8C(z)=1⇒C(z)=(z−2)(z−4)1
用反演积分法,可得:
c
(
n
T
)
=
R
e
s
[
C
(
z
)
⋅
z
n
−
1
]
z
→
2
+
R
e
s
[
C
(
z
)
⋅
z
n
−
1
]
z
→
4
=
lim
z
→
2
[
(
z
−
2
)
⋅
z
n
−
1
(
z
−
2
)
(
z
−
4
)
]
+
lim
z
→
4
[
(
z
−
4
)
⋅
z
n
−
1
(
z
−
2
)
(
z
−
4
)
]
=
−
2
n
−
2
+
2
2
n
−
3
(
n
=
2
,
3
,
4
,
⋯
)
begin{aligned} c(nT)&={rm Res}[C(z)·z^{n-1}]_{zto2}+{rm Res}[C(z)·z^{n-1}]_{zto4}\\ &=lim_{zto2}left[frac{(z-2)·z^{n-1}}{(z-2)(z-4)}right]+lim_{zto4}left[frac{(z-4)·z^{n-1}}{(z-2)(z-4)}right]\\ &=-2^{n-2}+2^{2n-3}(n=2,3,4,cdots) end{aligned}
c(nT)=Res[C(z)⋅zn−1]z→2+Res[C(z)⋅zn−1]z→4=z→2lim[(z−2)(z−4)(z−2)⋅zn−1]+z→4lim[(z−2)(z−4)(z−4)⋅zn−1]=−2n−2+22n−3(n=2,3,4,⋯)
故
c
(
0
)
=
c
(
1
)
=
0
,
c
(
2
)
=
1
,
c
(
3
)
=
6
,
c
(
4
)
=
28
,
⋯
c(0)=c(1)=0,c(2)=1,c(3)=6,c(4)=28,cdots
c(0)=c(1)=0,c(2)=1,c(3)=6,c(4)=28,⋯
Example 7.24
已知具有可变开环增益 K K K的采样系统如下图所示,其中采样周期 T = 1 T=1 T=1。
要求:
- 确定使系统稳定的 K K K值范围;
- 说明 T T T减小时,对使系统稳定的 K K K值范围有何影响?
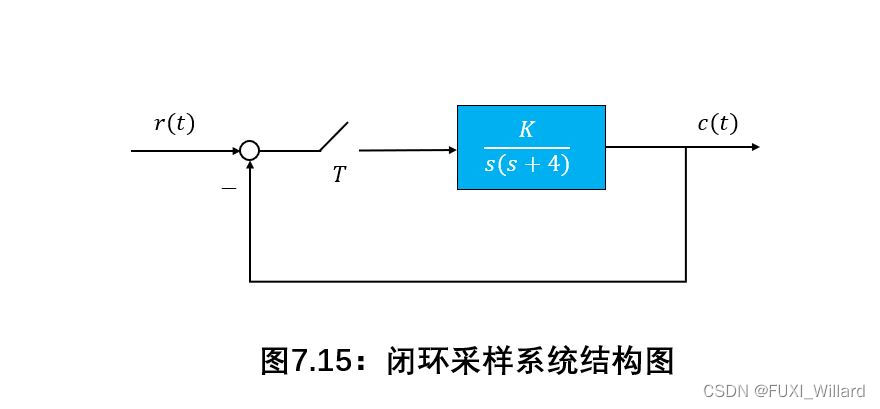
解:
-
系统稳定时的 K K K值范围。
开环脉冲传递函数为:
G ( z ) = Z [ K s ( s + 4 ) ] = K 4 ( 1 − e − 4 ) z ( z − 1 ) ( z − e − 4 ) = 0.9817 K z 4 ( z 2 − 1.0183 z + 0.0183 ) G(z)=Zleft[frac{K}{s(s+4)}right]=frac{K}{4}frac{(1-{rm e}^{-4})z}{(z-1)(z-{rm e}^{-4})}=frac{0.9817Kz}{4(z^2-1.0183z+0.0183)} G(z)=Z[s(s+4)K]=4K(z−1)(z−e−4)(1−e−4)z=4(z2−1.0183z+0.0183)0.9817Kz
则闭环脉冲传递函数为:
Φ ( z ) = G ( z ) 1 + G ( z ) = 0.9817 K z 4 z 2 + ( 0.9817 K − 4.0732 ) z + 0.0732 Phi(z)=frac{G(z)}{1+G(z)}=frac{0.9817Kz}{4z^2+(0.9817K-4.0732)z+0.0732} Φ(z)=1+G(z)G(z)=4z2+(0.9817K−4.0732)z+0.07320.9817Kz
特征方程为:
D ( z ) = 4 z 2 + ( 0.9817 K − 4.0732 ) z + 0.0732 = 0 D(z)=4z^2+(0.9817K-4.0732)z+0.0732=0 D(z)=4z2+(0.9817K−4.0732)z+0.0732=0
令 z = w + 1 w − 1 z=displaystylefrac{w+1}{w-1} z=w−1w+1,得:
0.9817 K w 2 + 7.8536 w + ( 8.1464 − 0.9817 K ) = 0 0.9817Kw^2+7.8536w+(8.1464-0.9817K)=0 0.9817Kw2+7.8536w+(8.1464−0.9817K)=0
劳斯表如下:w 2 w^2 w2 0.9817 K 0.9817K 0.9817K 8.1466 − 0.9817 K 8.1466-0.9817K 8.1466−0.9817K w 1 w^1 w1 7.8534 7.8534 7.8534 0 0 0 w 0 w^0 w0 8.1466 − 0.9817 K 8.1466-0.9817K 8.1466−0.9817K 为保证系统稳定,必须使 K > 0 K>0 K>0和 8.1466 − 0.9817 K > 0 8.1466-0.9817K>0 8.1466−0.9817K>0,解得: 0 < K < 8.2983 0<K<8.2983 0<K<8.2983。
【 K = 1 K=1 K=1和 K = 10 K=10 K=10时单位阶跃响应曲线】
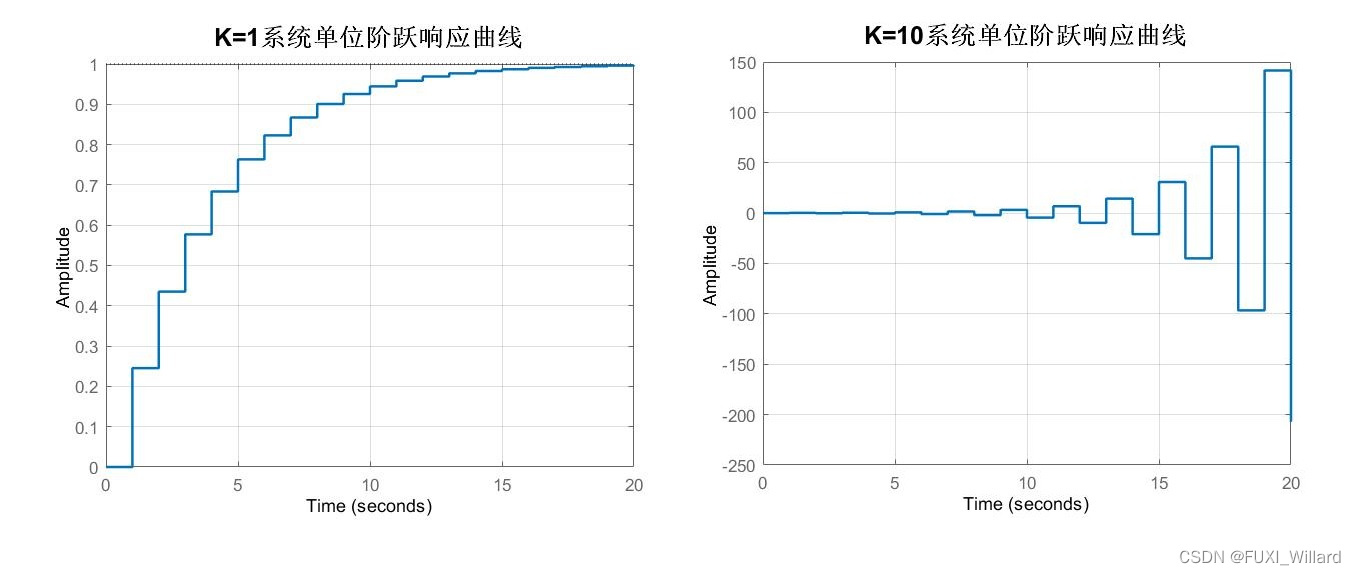
-
T T T对 K K K值范围的影响。
如果 T T T待定,有:
G ( z ) = K ( 1 − e − 4 T ) z 4 ( z − 1 ) ( z − e − 4 T ) Φ ( z ) = K ( 1 − e − 4 T ) z 4 z 2 + [ K ( 1 − e − 4 T ) − 4 ( 1 + e − 4 T ) ] z + 4 e − 4 T begin{aligned} &G(z)=frac{K(1-{rm e}^{-4T})z}{4(z-1)(z-{rm e}^{-4T})}\\ &Phi(z)=frac{K(1-{rm e}^{-4T})z}{4z^2+[K(1-{rm e}^{-4T})-4(1+{rm e}^{-4T})]z+4{rm e}^{-4T}} end{aligned} G(z)=4(z−1)(z−e−4T)K(1−e−4T)zΦ(z)=4z2+[K(1−e−4T)−4(1+e−4T)]z+4e−4TK(1−e−4T)z
令 z = w + 1 w − 1 z=displaystylefrac{w+1}{w-1} z=w−1w+1,得:
K ( 1 − e − 4 T ) w 2 + 8 ( 1 − e − 4 T ) w + 8 ( 1 + e − 4 T ) − K ( 1 − e − 4 T ) = 0 K(1-{rm e}^{-4T})w^2+8(1-{rm e}^{-4T})w+8(1+{rm e}^{-4T})-K(1-{rm e}^{-4T})=0 K(1−e−4T)w2+8(1−e−4T)w+8(1+e−4T)−K(1−e−4T)=0
劳斯表如下:w 2 w^2 w2 K ( 1 − e − 4 T ) K(1-{rm e}^{-4T}) K(1−e−4T) 8 ( 1 + e − 4 T ) − K ( 1 − e − 4 T ) 8(1+{rm e}^{-4T})-K(1-{rm e}^{-4T}) 8(1+e−4T)−K(1−e−4T) w 1 w^1 w1 8 ( 1 − e − 4 T ) 8(1-{rm e}^{-4T}) 8(1−e−4T) 0 0 0 w 0 w^0 w0 8 ( 1 + e − 4 T ) − K ( 1 − e − 4 T ) 8(1+{rm e}^{-4T})-K(1-{rm e}^{-4T}) 8(1+e−4T)−K(1−e−4T) 可见,当 0 < K < 8 ( 1 + e − 4 T ) 1 − e − 4 T 0<K<displaystylefrac{8(1+{rm e}^{-4T})}{1-{rm e}^{-4T}} 0<K<1−e−4T8(1+e−4T)时,系统稳定.此时若 T T T减小,则 K K K值范围将增大.
当 K = 10 , T = 1 K=10,T=1 K=10,T=1时,系统不稳定;当 T = 0.1 T=0.1 T=0.1时,使系统稳定得 K K K值范围为 0 < K < 40.75 0<K<40.75 0<K<40.75,取 K = 10 K=10 K=10.
【系统单位阶跃响应曲线】
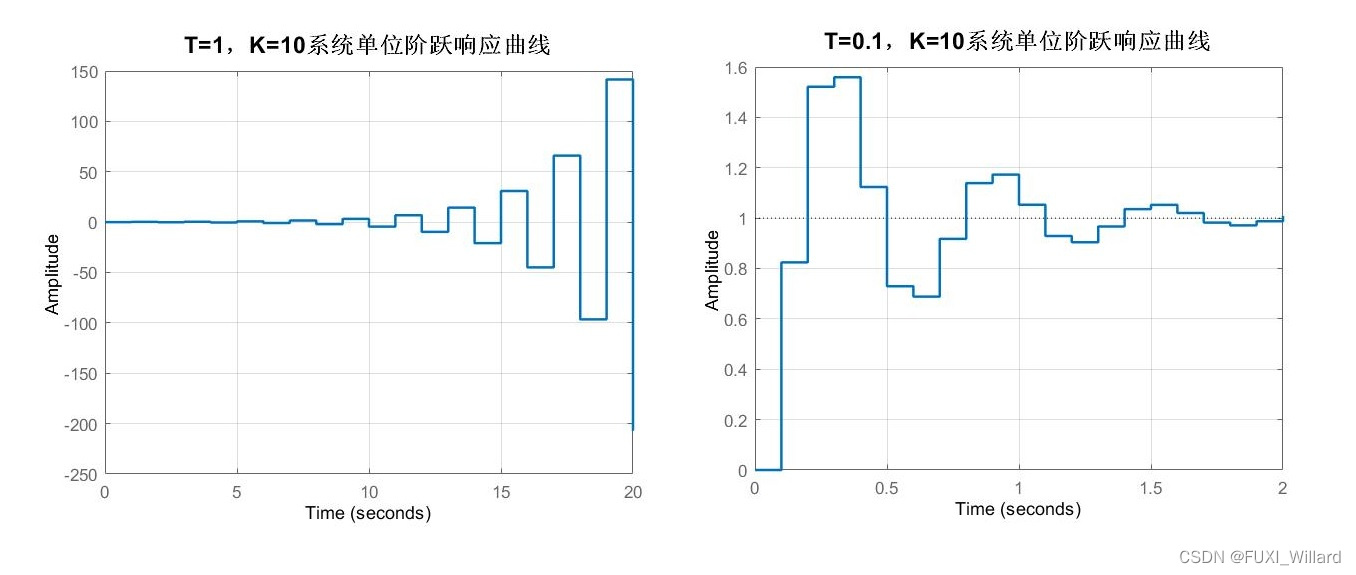
Example 7.25
采样系统结构图如下图所示:
- 输入 r ( t ) = 2 + t r(t)=2+t r(t)=2+t,欲使稳态误差小于 0.5 0.5 0.5,试选择 K K K值;
- 输入 r ( t ) = 1 ( t ) r(t)=1(t) r(t)=1(t),求系统过渡过程单调、振荡衰减和发散时, K K K值得范围;
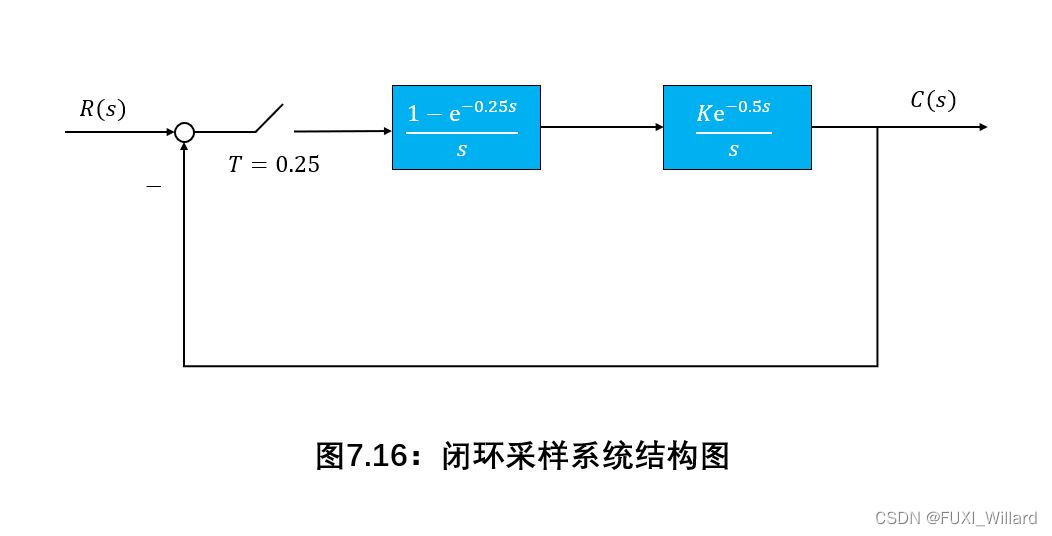
解:
-
K K K值选择。
开环脉冲传递函数为:
G ( z ) = Z [ 1 − e − T s s ⋅ K e − 0.5 s s ] = K ( 1 − z − 1 ) Z [ e − 0.5 s s 2 ] G(z)=Zleft[frac{1-{rm e}^{-Ts}}{s}·frac{K{rm e}^{-0.5s}}{s}right]=K(1-z^{-1})Zleft[frac{{rm e}^{-0.5s}}{s^2}right] G(z)=Z[s1−e−Ts⋅sKe−0.5s]=K(1−z−1)Z[s2e−0.5s]
由于 T = 0.25 T=0.25 T=0.25,故 e − 0.5 s = e − 2 T s = 1 z 2 {rm e}^{-0.5s}={rm e}^{-2Ts}=displaystylefrac{1}{z^2} e−0.5s=e−2Ts=z21,所以:
G ( z ) = 0.25 K z 2 ( z − 1 ) G(z)=frac{0.25K}{z^2(z-1)} G(z)=z2(z−1)0.25K
闭环误差脉冲传递函数为:
Φ e ( z ) = 1 1 + G ( z ) = z 2 ( z − 1 ) z 2 ( z − 1 ) + 0.25 K Phi_e(z)=frac{1}{1+G(z)}=frac{z^2(z-1)}{z^2(z-1)+0.25K} Φe(z)=1+G(z)1=z2(z−1)+0.25Kz2(z−1)
闭环特征方程为:
D ( z ) = z 3 − z 2 + 0.25 K = 0 D(z)=z^3-z^2+0.25K=0 D(z)=z3−z2+0.25K=0
将 z = w + 1 w − 1 z=displaystylefrac{w+1}{w-1} z=w−1w+1代入特征方程,得 w w w域特征方程:
D ( w ) = 0.25 K w 3 + ( 2 − 0.75 K ) w 2 + ( 4 + 0.75 K ) w + ( 2 − 0.25 K ) = 0 D(w)=0.25Kw^3+(2-0.75K)w^2+(4+0.75K)w+(2-0.25K)=0 D(w)=0.25Kw3+(2−0.75K)w2+(4+0.75K)w+(2−0.25K)=0
在 w w w域用劳斯判据分析系统的稳定性,可以得到使系统稳定的 K K K值范围.劳斯表如下:w 3 w^3 w3 0.25 K 0.25K 0.25K 4 + 0.75 K 4+0.75K 4+0.75K w 2 w^2 w2 2 − 0.75 K 2-0.75K 2−0.75K 2 − 0.25 K 2-0.25K 2−0.25K w 1 w^1 w1 ( 8 − 2 K − 0.5 K 2 ) / ( 2 − 0.75 K ) (8-2K-0.5K^2)/(2-0.75K) (8−2K−0.5K2)/(2−0.75K) 0 0 0 w 0 w^0 w0 2 − 0.25 K 2-0.25K 2−0.25K 由劳斯判据可知,使系统稳定的 K K K值范围:
{ K > 0 2 − 0.75 K > 0 8 − 2 K − 0.5 K 2 > 0 2 − 0.25 K > 0 ⇒ { K > 0 K < 2.6667 K < 8 K < 2.472 ⇒ 0 < K < 2.472 begin{cases} &K>0\ &2-0.75K>0\ &8-2K-0.5K^2>0\ &2-0.25K>0 end{cases}Rightarrow begin{cases} &K>0\ &K<2.6667\ &K<8\ &K<2.472 end{cases}Rightarrow 0<K<2.472 ⎩ ⎨ ⎧K>02−0.75K>08−2K−0.5K2>02−0.25K>0⇒⎩ ⎨ ⎧K>0K<2.6667K<8K<2.472⇒0<K<2.472
即使系统稳定的 K K K范围为: 0 < K < 2.472 0<K<2.472 0<K<2.472。从满足稳态误差要求考虑,由于
R ( z ) = Z [ 2 + t ] = 2 z z − 1 + T z ( z − 1 ) 2 = 2 z ( z − 1 ) + 0.25 z ( z − 1 ) 2 = z ( 2 z − 1.75 ) ( z − 1 ) 2 R(z)=Z[2+t]=frac{2z}{z-1}+frac{Tz}{(z-1)^2}=frac{2z(z-1)+0.25z}{(z-1)^2}=frac{z(2z-1.75)}{(z-1)^2} R(z)=Z[2+t]=z−12z+(z−1)2Tz=(z−1)22z(z−1)+0.25z=(z−1)2z(2z−1.75)
故稳态误差为:
e s s ( ∞ ) = lim z → 1 ( 1 − z − 1 ) Φ e ( z ) R ( z ) = 0.25 0.25 K = 1 K e_{ss}(infty)=lim_{zto1}(1-z^{-1})Phi_e(z)R(z)=frac{0.25}{0.25K}=frac{1}{K} ess(∞)=z→1lim(1−z−1)Φe(z)R(z)=0.25K0.25=K1
由于要求 e s s ( ∞ ) < 0.5 e_{ss}(infty)<0.5 ess(∞)<0.5,则有 K > 2.0 K>2.0 K>2.0。显然,满足 e s s ( ∞ ) = 0.5 e_{ss}(infty)=0.5 ess(∞)=0.5的 K K K值为: 2 < K < 2.472 2<K<2.472 2<K<2.472。 -
K K K值范围。
开环脉冲传递函数为:
G ( z ) = 0.25 K z 2 ( z − 1 ) G(z)=frac{0.25K}{z^2(z-1)} G(z)=z2(z−1)0.25K
开环系统在 z z z域中,有两个 z = 0 z=0 z=0的极点和一个 z = 1 z=1 z=1的极点.由 ∣ G ( z ) ∣ = 1 |G(z)|=1 ∣G(z)∣=1,有:
K = ∣ 4 z 2 ( z − 1 ) ∣ K=|4z^2(z-1)| K=∣4z2(z−1)∣
令 d K / d z = 0 {rm d}K/{rm d}z=0 dK/dz=0,可得:
3 z 2 − 2 z = 0 ⇒ z 1 = 0 , z 2 = 0.67 3z^2-2z=0Rightarrow{z_1}=0,z_2=0.67 3z2−2z=0⇒z1=0,z2=0.67
故 z = 0.67 z=0.67 z=0.67为分离点,对应
K = ∣ 4 z 2 ( z − 1 ) ∣ = 0.5925 K=|4z^2(z-1)|=0.5925 K=∣4z2(z−1)∣=0.5925
根轨迹如下图:
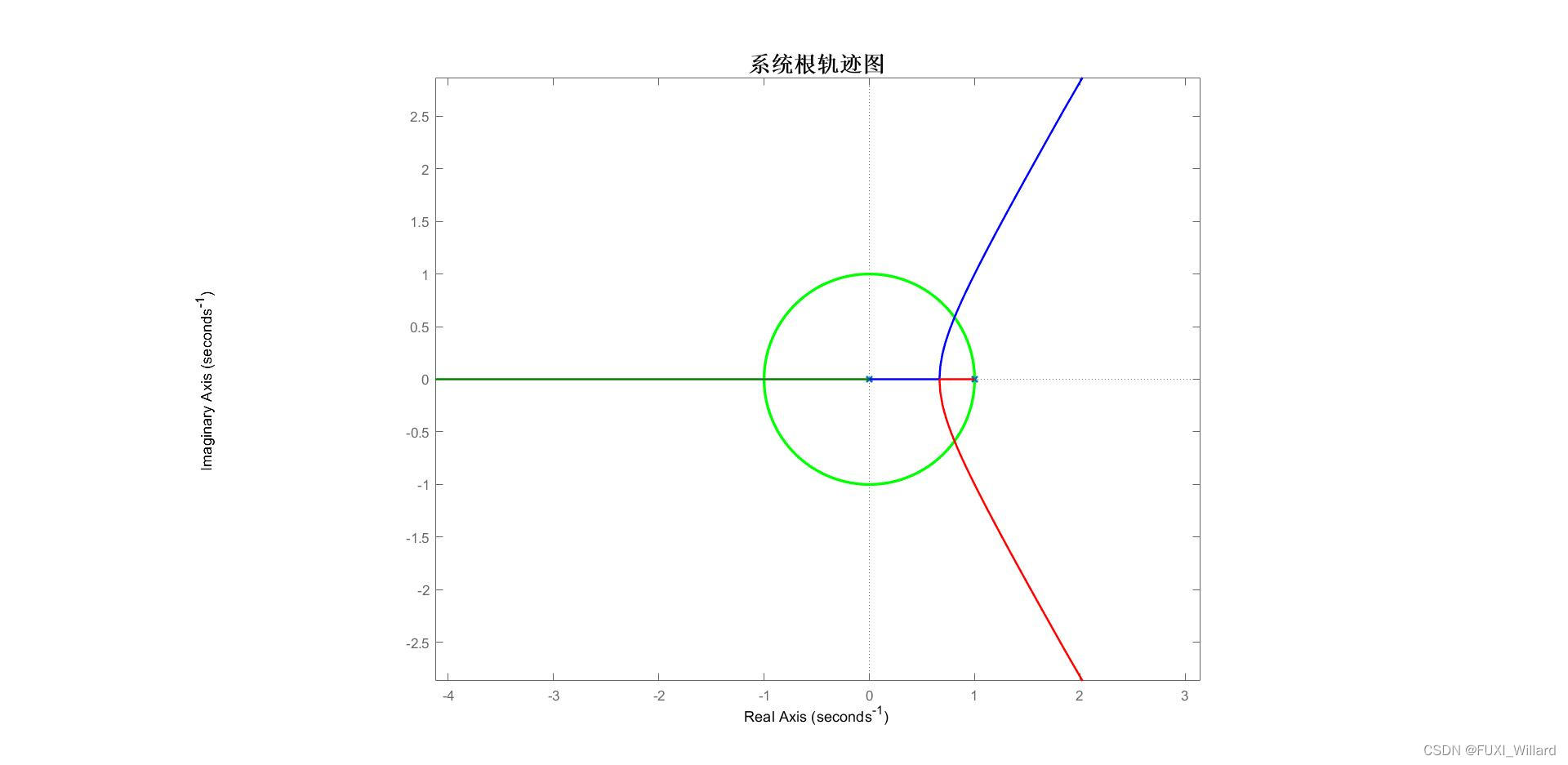
可得:- 0 < K < 0.5925 0<K<0.5925 0<K<0.5925时,系统过渡过程单调;
- 0.5925 < K < 2.472 0.5925<K<2.472 0.5925<K<2.472时,系统振荡衰减;
- K > 2.472 K>2.472 K>2.472时,系统发散;
-
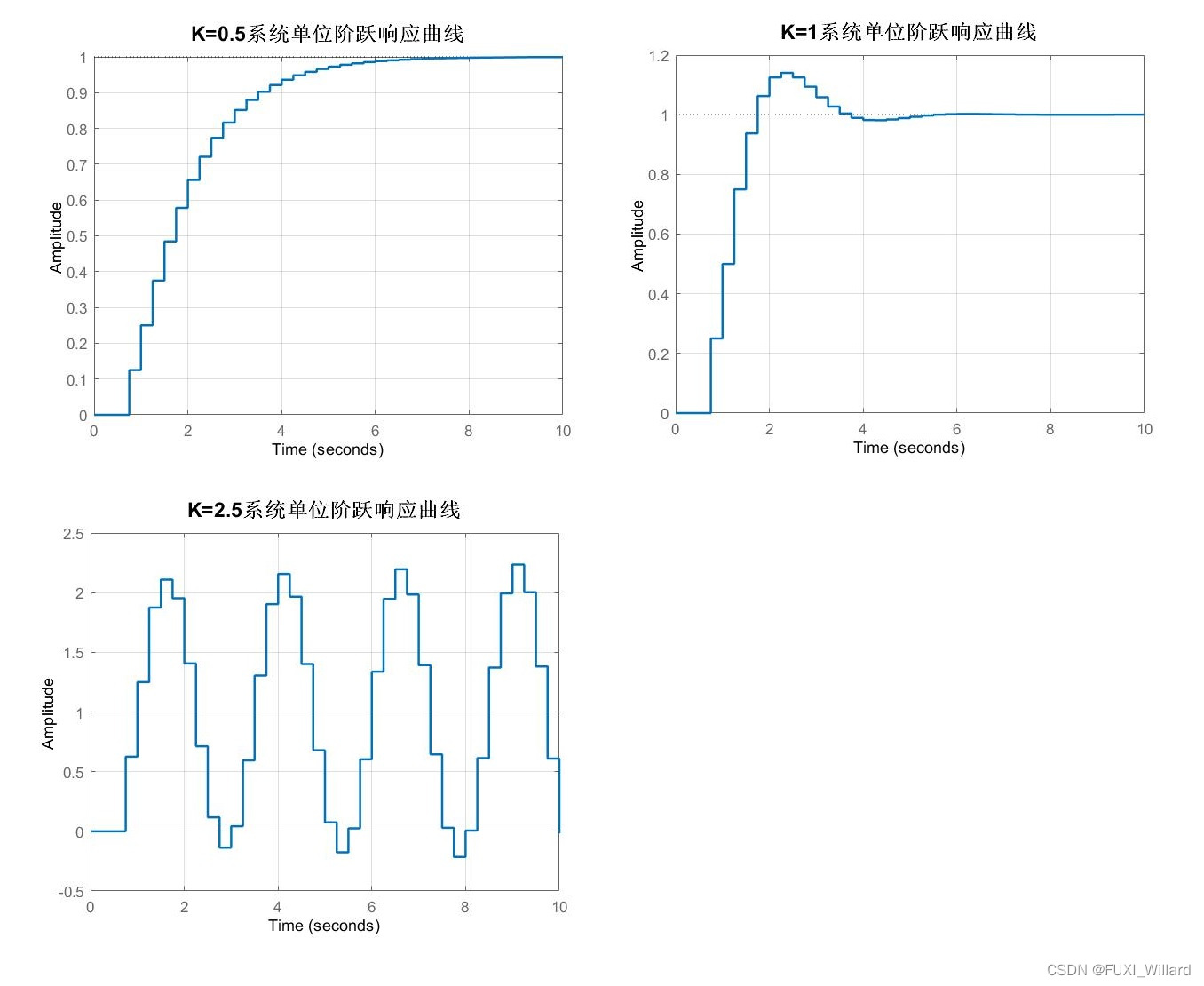
【系统不同 K K K值单位阶跃响应】
Example 7.26
采样系统的结构图如下图所示,图中采样周期 T = 0.1 T=0.1 T=0.1。确定在输入信号 r ( t ) = t r(t)=t r(t)=t作用下系统稳态误差 e s s ( ∞ ) = 0.05 e_{ss}(infty)=0.05 ess(∞)=0.05时的 K K K值。
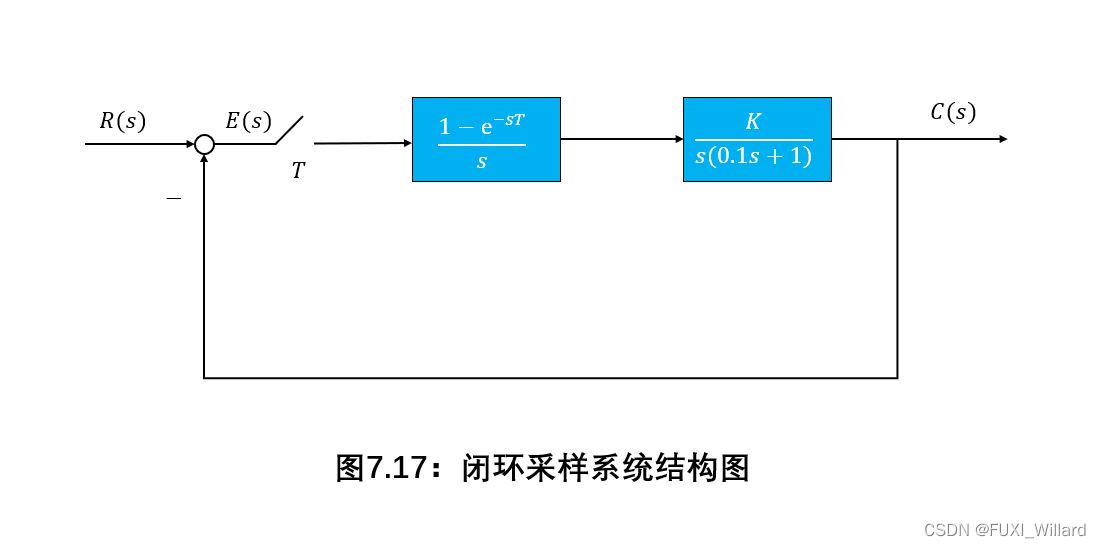
解:
开环脉冲传递函数为:
G
(
z
)
=
Z
[
(
1
−
e
−
s
T
)
K
s
2
(
0.1
s
+
1
)
]
=
K
(
1
−
z
−
1
)
Z
[
10
s
2
(
s
+
10
)
]
=
K
(
z
−
1
)
z
Z
[
1
s
2
−
0.1
s
+
0.1
s
+
10
]
=
K
(
z
−
1
)
z
[
T
z
(
z
−
1
)
2
−
0.1
z
z
−
1
+
0.1
z
z
−
e
−
1
]
=
K
[
e
−
1
z
+
(
1
−
2
e
−
1
)
]
10
(
z
−
1
)
(
z
−
e
−
1
)
=
K
(
0.3679
z
+
0.2642
)
10
(
z
−
1
)
(
z
−
0.3679
)
begin{aligned} G(z)&=Zleft[frac{(1-{rm e}^{-sT})K}{s^2(0.1s+1)}right]=K(1-z^{-1})Zleft[frac{10}{s^2(s+10)}right]=frac{K(z-1)}{z}Zleft[frac{1}{s^2}-frac{0.1}{s}+frac{0.1}{s+10}right]\\ &=frac{K(z-1)}{z}left[frac{Tz}{(z-1)^2}-frac{0.1z}{z-1}+frac{0.1z}{z-{rm e}^{-1}}right]=frac{K[{rm e}^{-1}z+(1-2{rm e}^{-1})]}{10(z-1)(z-{rm e}^{-1})}\\ &=frac{K(0.3679z+0.2642)}{10(z-1)(z-0.3679)} end{aligned}
G(z)=Z[s2(0.1s+1)(1−e−sT)K]=K(1−z−1)Z[s2(s+10)10]=zK(z−1)Z[s21−s0.1+s+100.1]=zK(z−1)[(z−1)2Tz−z−10.1z+z−e−10.1z]=10(z−1)(z−e−1)K[e−1z+(1−2e−1)]=10(z−1)(z−0.3679)K(0.3679z+0.2642)
闭环脉冲传递函数为:
Φ
(
z
)
=
G
(
z
)
1
+
G
(
z
)
=
K
(
0.3679
z
+
0.2642
)
10
z
2
+
(
0.3679
K
−
13.679
)
z
+
(
0.2642
K
+
3.679
)
Phi(z)=frac{G(z)}{1+G(z)}=frac{K(0.3679z+0.2642)}{10z^2+(0.3679K-13.679)z+(0.2642K+3.679)}
Φ(z)=1+G(z)G(z)=10z2+(0.3679K−13.679)z+(0.2642K+3.679)K(0.3679z+0.2642)
闭环特征方程为:
D
(
z
)
=
10
z
2
+
(
0.3679
K
−
13.679
)
z
+
(
0.2642
K
+
3.679
)
=
0
D(z)=10z^2+(0.3679K-13.679)z+(0.2642K+3.679)=0
D(z)=10z2+(0.3679K−13.679)z+(0.2642K+3.679)=0
令
z
=
w
+
1
w
−
1
z=displaystylefrac{w+1}{w-1}
z=w−1w+1,可得:
D
(
w
)
=
0.6321
K
w
2
+
(
12.642
−
0.5284
K
)
w
+
(
27.358
−
0.1037
K
)
=
0
D(w)=0.6321Kw^2+(12.642-0.5284K)w+(27.358-0.1037K)=0
D(w)=0.6321Kw2+(12.642−0.5284K)w+(27.358−0.1037K)=0
劳斯表如下:
| w 2 w^2 w2 | 0.6321 K 0.6321K 0.6321K | 27.358 − 0.1037 K 27.358-0.1037K 27.358−0.1037K |
|---|---|---|
| w 1 w^1 w1 | 12.642 − 0.5284 K 12.642-0.5284K 12.642−0.5284K | 0 0 0 |
| w 0 w^0 w0 | 27.358 − 0.1037 K 27.358-0.1037K 27.358−0.1037K |
由劳斯稳定判据可知,当 0 < K < 23.925 0<K<23.925 0<K<23.925时系统稳定.
根据开环脉冲传递函数的形式,该系统是Ⅰ型系统,在单位斜坡输入的情况下,稳态误差为:
e
s
s
(
∞
)
=
T
K
v
e_{ss}(infty)=frac{T}{K_v}
ess(∞)=KvT
其中:
K
v
=
lim
z
→
1
(
z
−
1
)
G
(
z
)
=
K
10
K_v=lim_{zto1}(z-1)G(z)=frac{K}{10}
Kv=z→1lim(z−1)G(z)=10K
则有
e
s
s
(
∞
)
=
T
K
v
=
1
K
=
0.05
⇒
K
=
20
e_{ss}(infty)=frac{T}{K_v}=frac{1}{K}=0.05Rightarrow{K=20}
ess(∞)=KvT=K1=0.05⇒K=20
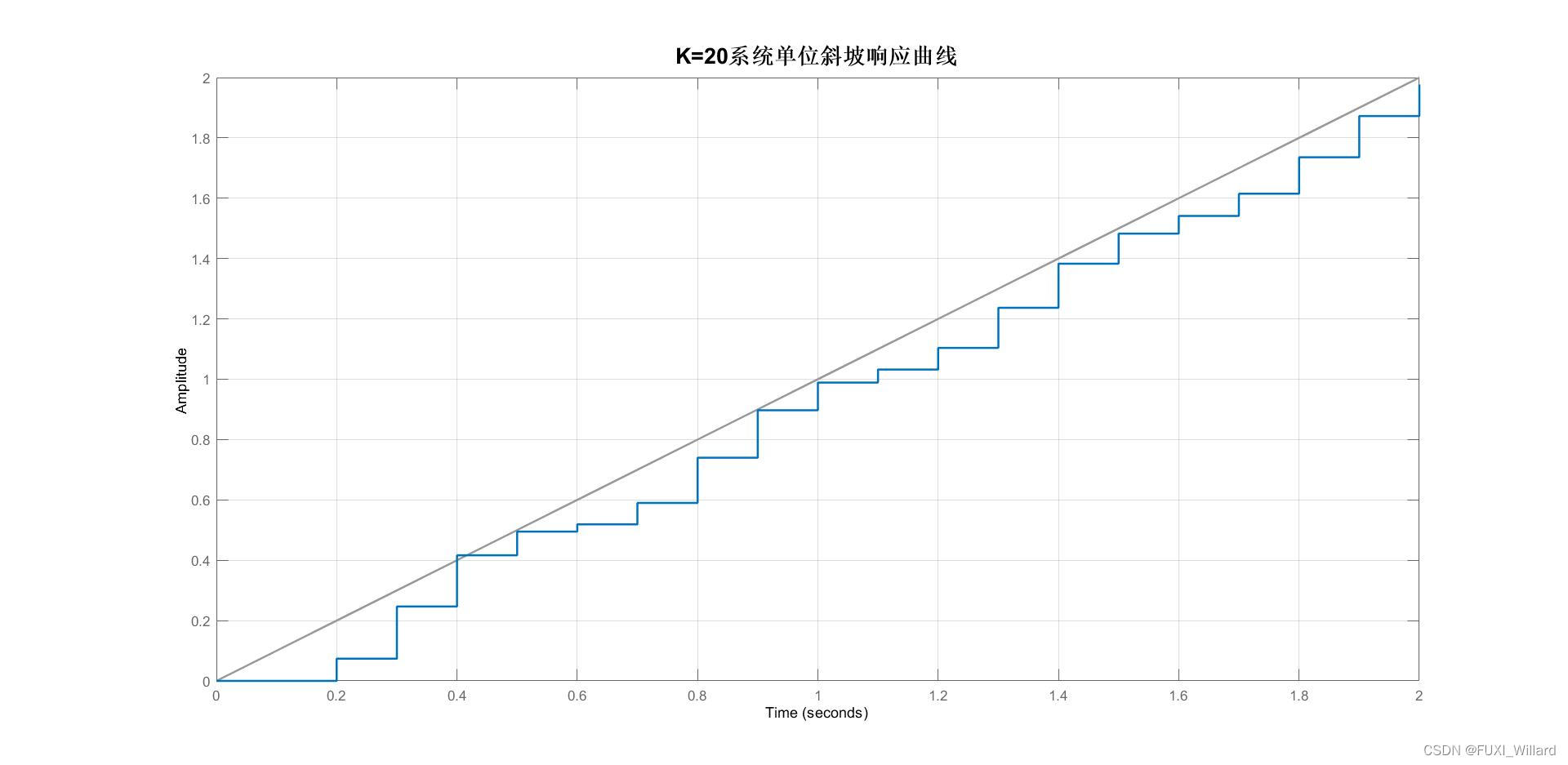
【系统单位斜坡响应曲线】
Example 7.27
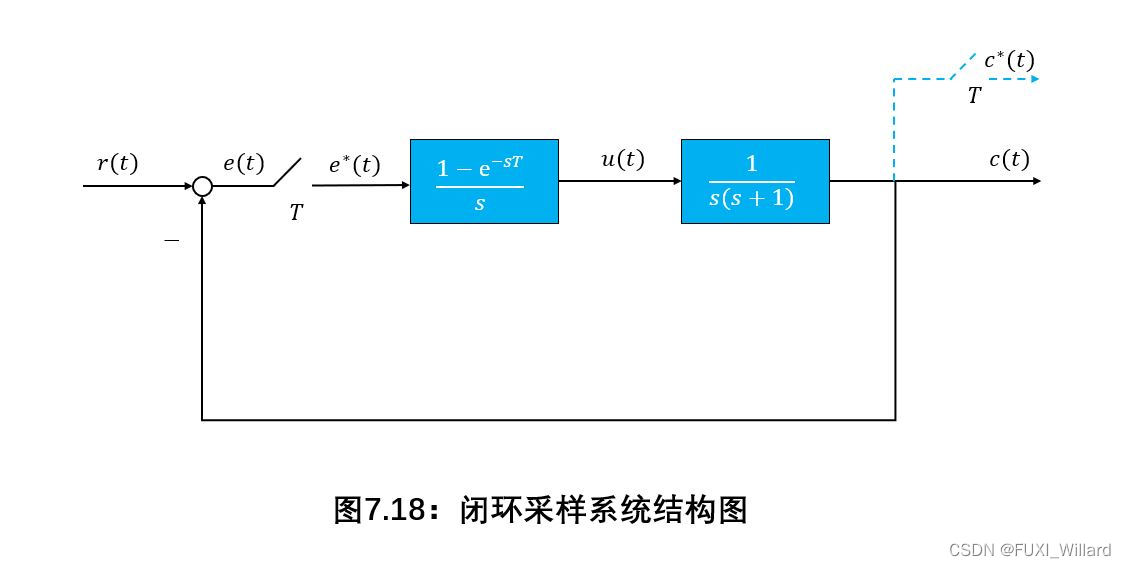
采样系统结构图如下图所示。设采样周期 T = 1 , r ( t ) = 1 ( t ) T=1,r(t)=1(t) T=1,r(t)=1(t)。
- 求系统脉冲传递函数;
- 求系统的输出响应 c ∗ ( t ) c^*(t) c∗(t)(算至 n = 5 n=5 n=5);
- 画出 c ∗ ( t ) , e ∗ ( t ) , u ( t ) c^*(t),e^*(t),u(t) c∗(t),e∗(t),u(t)的响应曲线。
解:
-
系统脉冲传递函数。
开环脉冲传递函数为:
G ( z ) = Z [ 1 − e − T s s 2 ( s + 1 ) ] = ( 1 − z − 1 ) Z [ 1 s 2 ( s + 1 ) ] = z − 1 z ⋅ [ z ( z − 1 ) 2 ⋅ ( 1 − e − 1 ) z ( z − 1 ) ( z − e − 1 ) ] = e − 1 z + 1 − 2 e − 1 ( z − 1 ) ( z − e − 1 ) = 0.3679 z + 0.2642 z 2 − 1.3679 z + 0.3679 begin{aligned} G(z)&=Zleft[frac{1-{rm e}^{-Ts}}{s^2(s+1)}right]=(1-z^{-1})Zleft[frac{1}{s^2(s+1)}right]\\ &=frac{z-1}{z}·left[frac{z}{(z-1)^2}·frac{(1-{rm e}^{-1})z}{(z-1)(z-{rm e}^{-1})}right]=frac{{rm e}^{-1}z+1-2{rm e}^{-1}}{(z-1)(z-{rm e}^{-1})}\\ &=frac{0.3679z+0.2642}{z^2-1.3679z+0.3679} end{aligned} G(z)=Z[s2(s+1)1−e−Ts]=(1−z−1)Z[s2(s+1)1]=zz−1⋅[(z−1)2z⋅(z−1)(z−e−1)(1−e−1)z]=(z−1)(z−e−1)e−1z+1−2e−1=z2−1.3679z+0.36790.3679z+0.2642
闭环脉冲传递函数为:
Φ ( z ) = G ( z ) 1 + G ( z ) = e − 1 z + 1 − 2 e − 1 z 2 − z + 1 − e − 1 = 0.3679 z + 0.2642 z 2 − z + 0.6321 Phi(z)=frac{G(z)}{1+G(z)}=frac{{rm e}^{-1}z+1-2{rm e}^{-1}}{z^2-z+1-{rm e}^{-1}}=frac{0.3679z+0.2642}{z^2-z+0.6321} Φ(z)=1+G(z)G(z)=z2−z+1−e−1e−1z+1−2e−1=z2−z+0.63210.3679z+0.2642 -
输出响应 c ∗ ( t ) c^*(t) c∗(t)。
输入 z z z变换为:
R ( z ) = z z − 1 R(z)=frac{z}{z-1} R(z)=z−1z
可得输出为:
C ( z ) = G ( z ) 1 + G ( z ) ⋅ R ( z ) = 0.3679 z 2 + 0.2642 z z 3 − 2 z 2 + 1.6321 z − 0.6321 = 0.3679 z − 1 + z − 2 + 1.3996 z − 3 + 1.3996 z − 4 + 1.147 z − 5 + ⋯ + begin{aligned} C(z)&=frac{G(z)}{1+G(z)}·R(z)=frac{0.3679z^2+0.2642z}{z^3-2z^2+1.6321z-0.6321}\\ &=0.3679z^{-1}+z^{-2}+1.3996z^{-3}+1.3996z^{-4}+1.147z^{-5}+cdots+ end{aligned} C(z)=1+G(z)G(z)⋅R(z)=z3−2z2+1.6321z−0.63210.3679z2+0.2642z=0.3679z−1+z−2+1.3996z−3+1.3996z−4+1.147z−5+⋯+ -
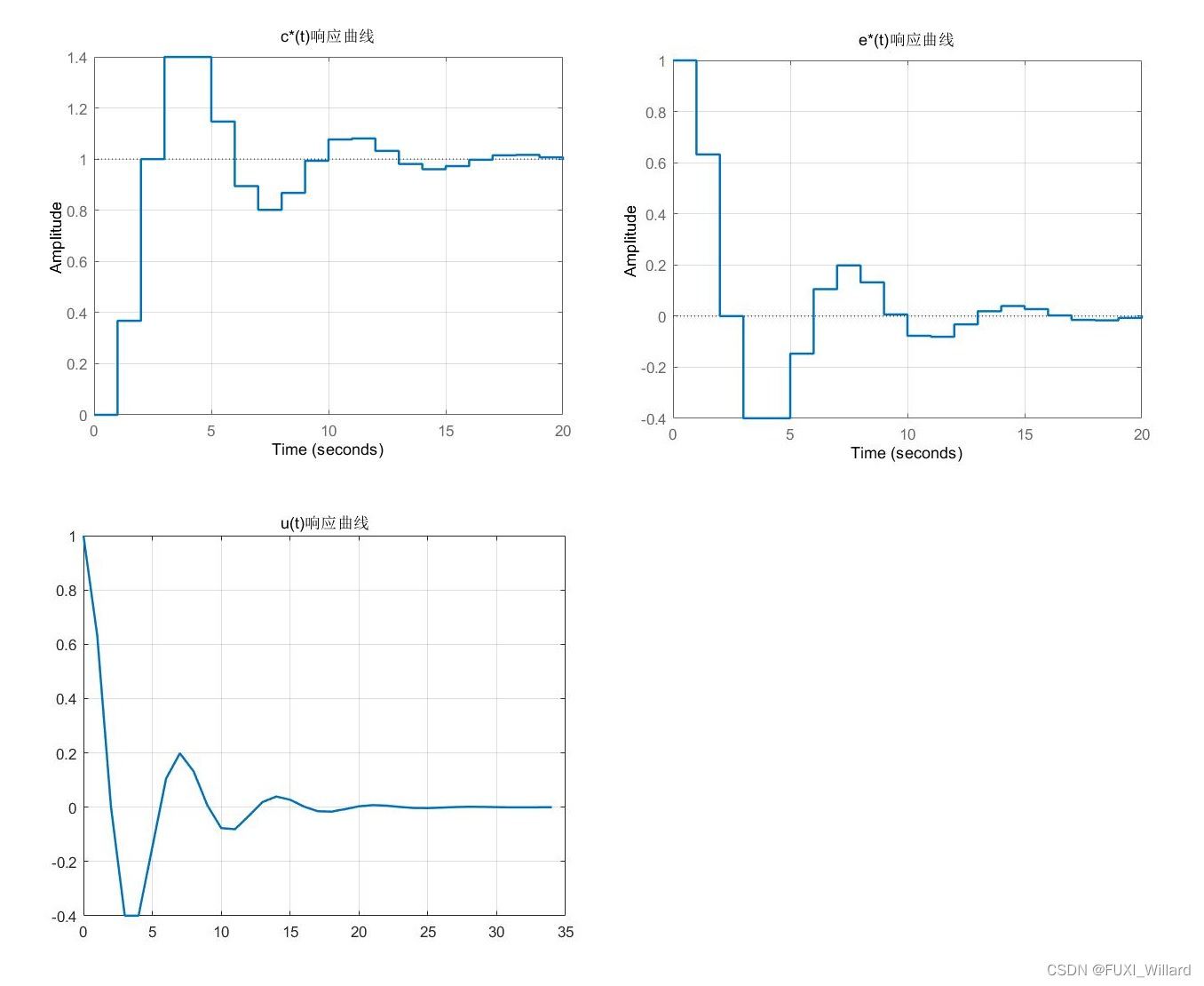
响应曲线。
系统误差闭环脉冲传递函数为:
Φ e ( z ) = 1 1 + G ( z ) = z 2 − 1.3679 z + 0.3679 z 2 − z + 0.6321 , E ( z ) = Φ e ( z ) R ( z ) Phi_e(z)=frac{1}{1+G(z)}=frac{z^2-1.3679z+0.3679}{z^2-z+0.6321},E(z)=Phi_e(z)R(z) Φe(z)=1+G(z)1=z2−z+0.6321z2−1.3679z+0.3679,E(z)=Φe(z)R(z)
【 c ∗ ( t ) 、 e ∗ ( t ) 、 u ( t ) c^*(t)、e^*(t)、u(t) c∗(t)、e∗(t)、u(t)响应曲线】
Example 7.28
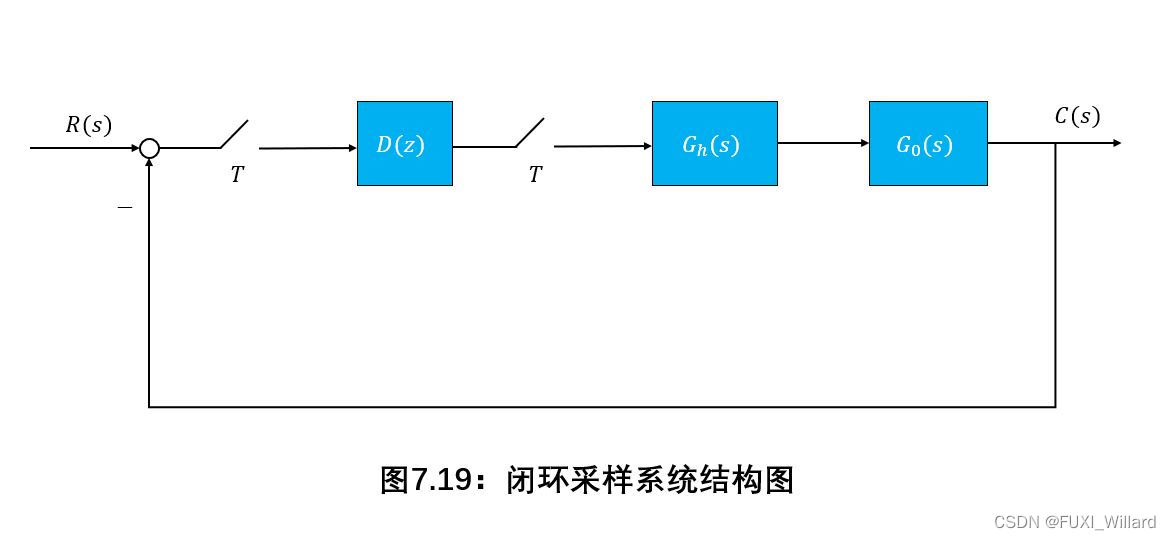
采样系统结构图如下图所示,其中控制对象的传递函数为: G 0 ( s ) = 10 s ( s + 1 ) G_0(s)=displaystylefrac{10}{s(s+1)} G0(s)=s(s+1)10, G h ( s ) G_h(s) Gh(s)是零阶保持器,采样周期 T = 1 T=1 T=1。当单位斜坡输入时,按使系统具有最快响应特性来设计 D ( z ) D(z) D(z)。
解:
开环脉冲传递函数为:
G
(
z
)
=
Z
[
10
(
1
−
e
−
T
s
)
s
2
(
s
+
1
)
]
=
10
(
1
−
z
−
1
)
Z
[
1
s
2
(
s
+
1
)
]
=
10
(
z
−
1
)
z
[
z
(
z
−
1
)
2
−
(
1
−
e
−
1
)
z
(
z
−
1
)
(
z
−
e
−
1
)
]
=
10
(
e
−
1
z
+
1
−
2
e
−
1
)
(
z
−
1
)
(
z
−
e
−
1
)
=
10
(
0.368
z
+
0.264
)
(
z
−
1
)
(
z
−
0.368
)
begin{aligned} G(z)&=Zleft[frac{10(1-{rm e}^{-Ts})}{s^2(s+1)}right]=10(1-z^{-1})Zleft[frac{1}{s^2(s+1)}right]\\ &=frac{10(z-1)}{z}left[frac{z}{(z-1)^2}-frac{(1-{rm e}^{-1})z}{(z-1)(z-{rm e}^{-1})}right]=frac{10({rm e}^{-1}z+1-2{rm e}^{-1})}{(z-1)(z-{rm e}^{-1})}\\ &=frac{10(0.368z+0.264)}{(z-1)(z-0.368)} end{aligned}
G(z)=Z[s2(s+1)10(1−e−Ts)]=10(1−z−1)Z[s2(s+1)1]=z10(z−1)[(z−1)2z−(z−1)(z−e−1)(1−e−1)z]=(z−1)(z−e−1)10(e−1z+1−2e−1)=(z−1)(z−0.368)10(0.368z+0.264)
针对单位斜坡输入,最少拍系统的闭环脉冲传递函数为:
Φ
(
z
)
=
2
z
−
1
−
z
−
2
Phi(z)=2z^{-1}-z^{-2}
Φ(z)=2z−1−z−2
则有
D
(
z
)
=
Φ
(
z
)
G
(
z
)
(
1
−
Φ
(
z
)
)
=
(
2
z
−
1
)
(
z
−
e
−
1
)
10
(
z
−
1
)
(
e
−
1
z
+
1
−
2
e
−
1
)
=
(
2
z
−
1
)
(
z
−
0.3679
)
(
z
−
1
)
(
3.679
z
+
2.642
)
D(z)=frac{Phi(z)}{G(z)(1-Phi(z))}=frac{(2z-1)(z-{rm e}^{-1})}{10(z-1)({rm e}^{-1}z+1-2{rm e}^{-1})}=frac{(2z-1)(z-0.3679)}{(z-1)(3.679z+2.642)}
D(z)=G(z)(1−Φ(z))Φ(z)=10(z−1)(e−1z+1−2e−1)(2z−1)(z−e−1)=(z−1)(3.679z+2.642)(2z−1)(z−0.3679)
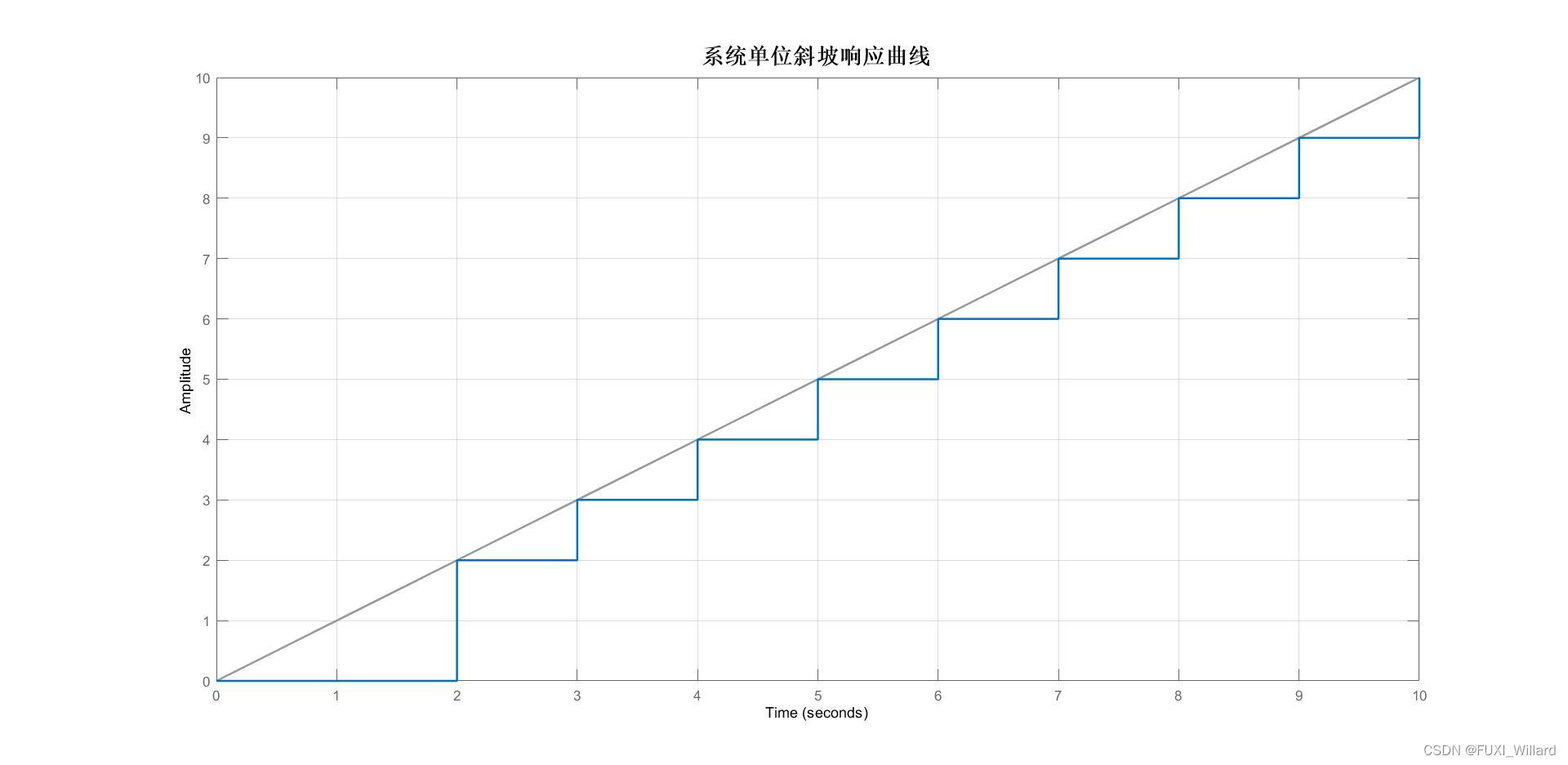
【输出响应曲线】
Example 7.29
采样系统的结构图如下图所示。要求:
- 求系统闭环脉冲传递函数 C ( z ) R ( z ) displaystylefrac{C(z)}{R(z)} R(z)C(z);
- 当初始条件为零,输入量 r ( t ) r(t) r(t)为单位阶跃函数时,求系统的输出 c ( k ) , k = 0 , 1 , 2 , 3 c(k),k=0,1,2,3 c(k),k=0,1,2,3,并画出其波形图;
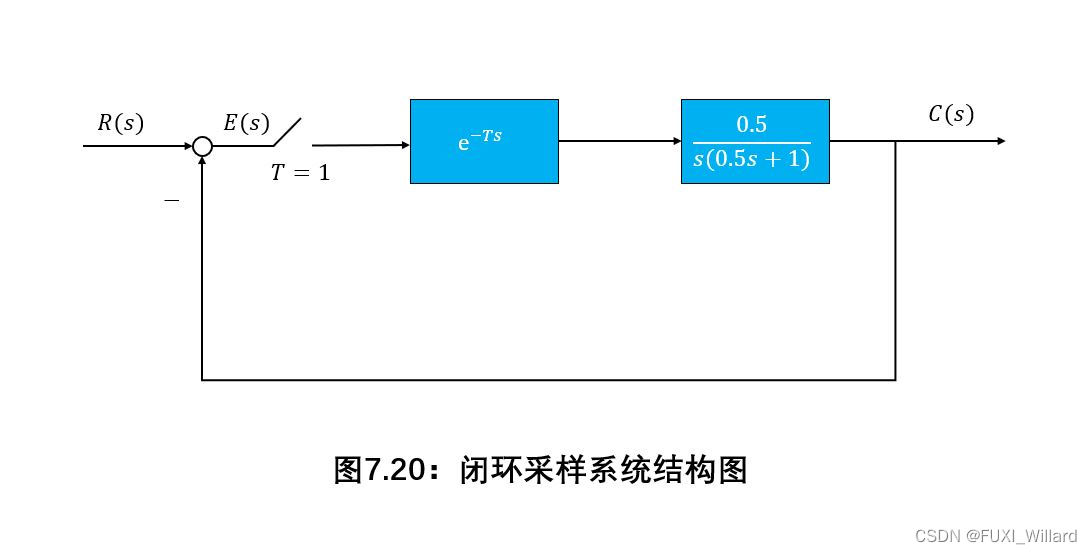
解:
-
求传递函数。
系统开环脉冲传递函数为:
G ( z ) = Z [ 0.5 e − T s s ( 0.5 s + 1 ) ] = z − 1 Z [ 1 s ( s + 2 ) ] = 1 2 z ⋅ ( 1 − e − 2 ) z ( z − 1 ) ( z − e − 2 ) = 0.4323 ( z − 1 ) ( z − 0.1353 ) begin{aligned} G(z)&=Zleft[frac{0.5{rm e}^{-Ts}}{s(0.5s+1)}right]=z^{-1}Zleft[frac{1}{s(s+2)}right]=frac{1}{2z}·frac{(1-{rm e}^{-2})z}{(z-1)(z-{rm e}^{-2})}=frac{0.4323}{(z-1)(z-0.1353)} end{aligned} G(z)=Z[s(0.5s+1)0.5e−Ts]=z−1Z[s(s+2)1]=2z1⋅(z−1)(z−e−2)(1−e−2)z=(z−1)(z−0.1353)0.4323
系统闭环脉冲传递函数为:
Φ ( z ) = C ( z ) R ( z ) = G ( z ) 1 + G ( z ) = 0.4323 z 2 − 1.1353 z + 0.5676 Phi(z)=frac{C(z)}{R(z)}=frac{G(z)}{1+G(z)}=frac{0.4323}{z^2-1.1353z+0.5676} Φ(z)=R(z)C(z)=1+G(z)G(z)=z2−1.1353z+0.56760.4323 -
求输出 c ( k ) c(k) c(k)。
输入 z z z变换为: R ( z ) = z z − 1 R(z)=displaystylefrac{z}{z-1} R(z)=z−1z。
有
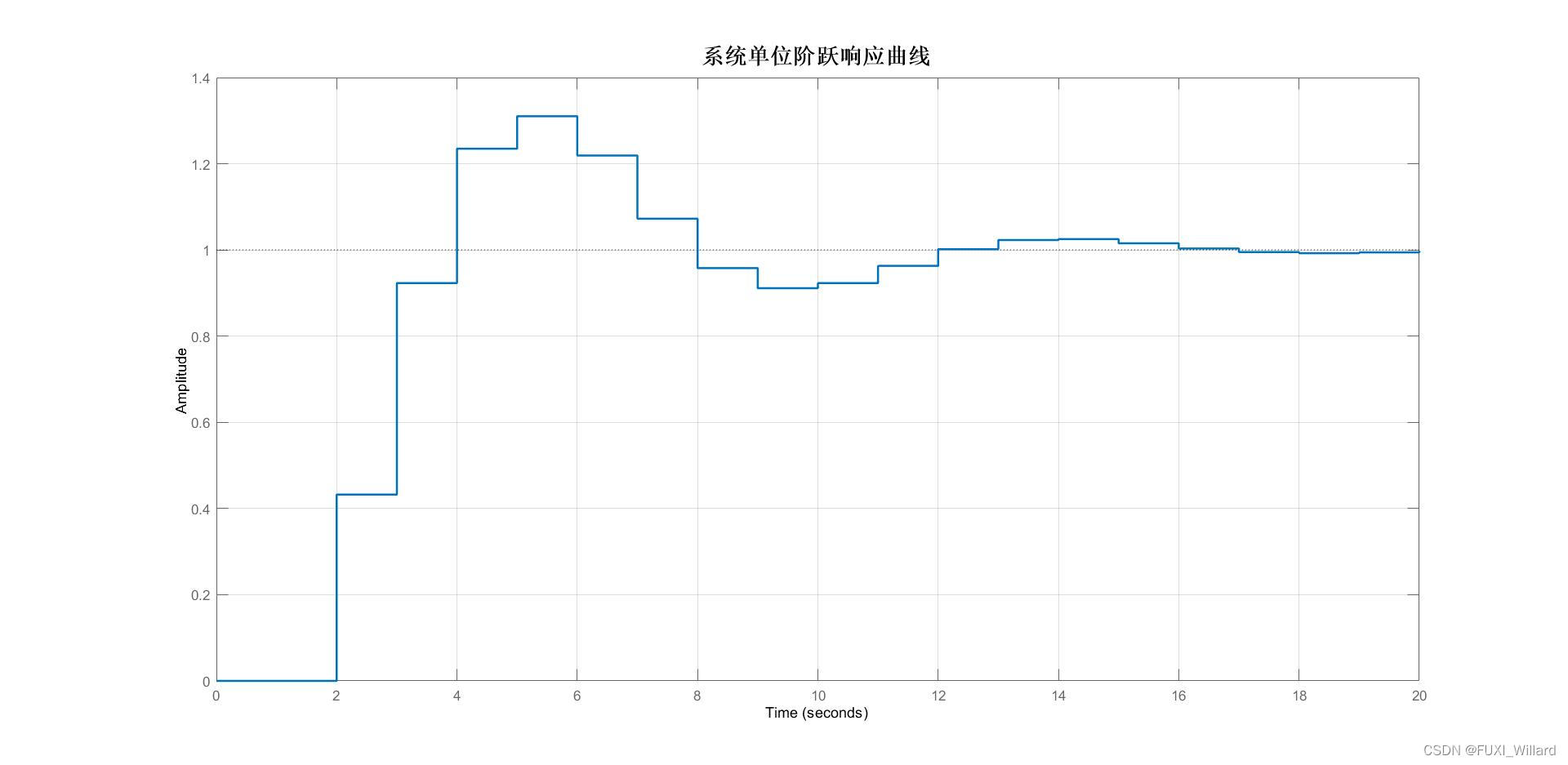
C ( z ) = Φ ( z ) R ( z ) = 0.4323 z z 3 − 2.1353 z 2 + 1.7029 z − 0.5676 = 0.4323 z − 2 + 0.9231 z − 3 + 1.2349 z − 4 + ⋯ + c ( 0 ) = 0 , c ( 1 ) = 0 , c ( 2 ) = 0.4323 , c ( 3 ) = 0.9231 begin{aligned} C(z)&=Phi(z)R(z)=frac{0.4323z}{z^3-2.1353z^2+1.7029z-0.5676}\\ &=0.4323z^{-2}+0.9231z^{-3}+1.2349z^{-4}+cdots+\\ c(0)&=0,c(1)=0,c(2)=0.4323,c(3)=0.9231 end{aligned} C(z)c(0)=Φ(z)R(z)=z3−2.1353z2+1.7029z−0.56760.4323z=0.4323z−2+0.9231z−3+1.2349z−4+⋯+=0,c(1)=0,c(2)=0.4323,c(3)=0.9231
【 c ( k ) c(k) c(k)波形图】
Example 7.30
采样系统的结构图如下图所示,两采样器同步采样,采样周期 T = 1 T=1 T=1,并假设满足香农 ( S h a n n o n ) ({rm Shannon}) (Shannon)采样定理。
要求:
- 求采样系统的误差脉冲传递函数 E ( z ) / R ( z ) E(z)/R(z) E(z)/R(z);
- 判别系统的稳定性;
- 当 r ( t ) = 10 ⋅ 1 ( t ) r(t)=10·1(t) r(t)=10⋅1(t)时,求系统的稳态误差;
- 当 r ( t ) = 10 ⋅ 1 ( t ) r(t)=10·1(t) r(t)=10⋅1(t)时,求系统误差采样信号 e ∗ ( t ) e^*(t) e∗(t)在前 4 4 4个采样时刻的值 e ( k T ) , k = 0 , 1 , 2 , 3 e(kT),k=0,1,2,3 e(kT),k=0,1,2,3,并画出其波形图;
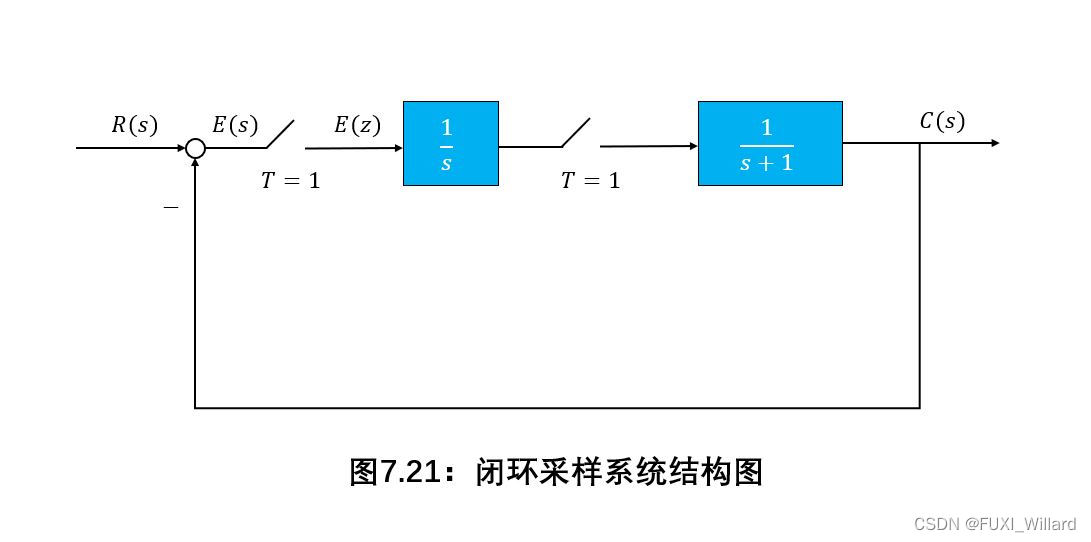
解:
-
求传递函数。
开环脉冲传递函数为:
G 1 ( z ) G 2 ( z ) = Z [ 1 s ] ⋅ Z [ 1 s + 1 ] = z z − 1 ⋅ z z − e − 1 = z 2 z 2 − 1.3679 z + 0.3679 G_1(z)G_2(z)=Zleft[frac{1}{s}right]·Zleft[frac{1}{s+1}right]=frac{z}{z-1}·frac{z}{z-{rm e}^{-1}}=frac{z^2}{z^2-1.3679z+0.3679} G1(z)G2(z)=Z[s1]⋅Z[s+11]=z−1z⋅z−e−1z=z2−1.3679z+0.3679z2
误差脉冲传递函数为:
Φ e ( z ) = E ( z ) R ( z ) = 1 1 + G 1 ( z ) G 2 ( z ) = z 2 − 1.3679 z + 0.3679 2 z 2 − 1.3679 z + 0.3679 Phi_e(z)=frac{E(z)}{R(z)}=frac{1}{1+G_1(z)G_2(z)}=frac{z^2-1.3679z+0.3679}{2z^2-1.3679z+0.3679} Φe(z)=R(z)E(z)=1+G1(z)G2(z)1=2z2−1.3679z+0.3679z2−1.3679z+0.3679 -
系统稳定性。
闭环特征方程为:
D ( z ) = 2 z 2 − 1.3679 z + 0.3679 = 0 ⇒ z 1 , 2 = 0.3420 ± j 0.2588 D(z)=2z^2-1.3679z+0.3679=0Rightarrow{z_{1,2}}=0.3420±{rm j}0.2588 D(z)=2z2−1.3679z+0.3679=0⇒z1,2=0.3420±j0.2588
因为 ∣ z 1 , 2 ∣ = 0.4289 < 1 |z_{1,2}|=0.4289<1 ∣z1,2∣=0.4289<1,所以闭环系统稳定. -
系统稳态误差。
输入 z z z变换为: R ( z ) = 10 z z − 1 R(z)=displaystylefrac{10z}{z-1} R(z)=z−110z。
采样误差函数为:
E ( z ) = Φ e ( z ) R ( z ) = z 2 − 1.3679 z + 0.3679 2 z 2 − 1.3679 z + 0.3679 ⋅ 10 z z − 1 E(z)=Phi_e(z)R(z)=frac{z^2-1.3679z+0.3679}{2z^2-1.3679z+0.3679}·frac{10z}{z-1} E(z)=Φe(z)R(z)=2z2−1.3679z+0.3679z2−1.3679z+0.3679⋅z−110z
稳态误差为:
e s s ( ∞ ) = lim z → 1 ( 1 − z − 1 ) E ( z ) = lim z → 1 z − 1 z ⋅ z 2 − 1.3679 z + 0.3679 2 z 2 − 1.3679 z + 0.3679 ⋅ 10 z z − 1 = 0 e_{ss}(infty)=lim_{zto1}(1-z^{-1})E(z)=lim_{zto1}frac{z-1}{z}·frac{z^2-1.3679z+0.3679}{2z^2-1.3679z+0.3679}·frac{10z}{z-1}=0 ess(∞)=z→1lim(1−z−1)E(z)=z→1limzz−1⋅2z2−1.3679z+0.3679z2−1.3679z+0.3679⋅z−110z=0 -
误差采样信号及波形图。
E ( z ) = z 2 − 1.3679 z + 0.3679 2 z 2 − 1.3679 z + 0.3679 ⋅ 10 z z − 1 = 10 z 3 − 13.679 z 2 + 3.679 z 2 z 3 − 3.3679 z 2 + 1.7358 z − 0.3679 = 5 + 1.58 z − 1 + 0.161 z − 2 − 0.181 z − 3 − 0.153 z − 4 + ⋯ + begin{aligned} E(z)&=frac{z^2-1.3679z+0.3679}{2z^2-1.3679z+0.3679}·frac{10z}{z-1}=frac{10z^3-13.679z^2+3.679z}{2z^3-3.3679z^2+1.7358z-0.3679}\\ &=5+1.58z^{-1}+0.161z^{-2}-0.181z^{-3}-0.153z^{-4}+cdots+ end{aligned} E(z)=2z2−1.3679z+0.3679z2−1.3679z+0.3679⋅z−110z=2z3−3.3679z2+1.7358z−0.367910z3−13.679z2+3.679z=5+1.58z−1+0.161z−2−0.181z−3−0.153z−4+⋯+
则有
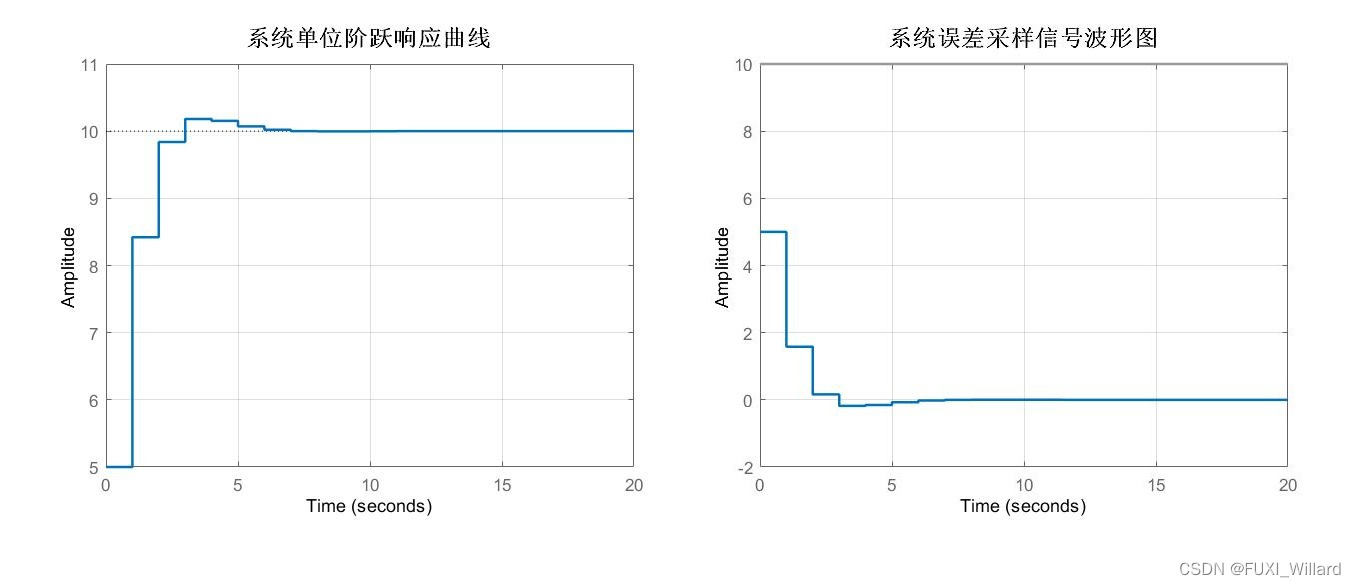
e ( 0 ) = 5 , e ( 1 ) = 1.58 , e ( 2 ) = 0.161 , e ( 3 ) = − 0.181 e(0)=5,e(1)=1.58,e(2)=0.161,e(3)=-0.181 e(0)=5,e(1)=1.58,e(2)=0.161,e(3)=−0.181 -
【单位阶跃响应曲线和误差采样信号波形图】
最后
以上就是现实酒窝最近收集整理的关于Chapter7.3:线性离散系统的分析与校正的全部内容,更多相关Chapter7.3:线性离散系统内容请搜索靠谱客的其他文章。








发表评论 取消回复