Machine Learning 学习笔记(四)———Matlab基础教程

Machine Learning 学习笔记(四)——Matlab基础教程

1.基本操作

• 计算数值

  >> 5 + 6
  ans = 11
  >> 3 * 4
  ans = 12
  >> 1/3
  ans = 0.3333
  >> 2^6
  ans = 64
  

• 计算逻辑值

  >> 1 == 2
  ans = 0
  >> 1 ~= 2 
  ans = 1
  >> 1 && 0
  ans = 0
  >> 1 || 0
  ans = 1
  

• 变量

  >> a = 6
  a = 6
  >> a = 6;  %加上分号可以使变量不打印输出
  >>
  

• 打印变量

  >> a = pi;
  >> a       
  a = 3.1416
  >> disp(a)       %仅输出a的值
      3.1416
  >> disp(sprintf("2 decimals : %0.2f",a))  %打印字符串（用c语言的格式）
  2 decimals : 3.14
  >> 
  

• 建立矩阵和向量

  >> A = [1 2;3 4;5 6]  %分号代表矩阵的换行
  A =
       1     2
       3     4
       5     6
  >> v = [1 2 3]     %表示行向量（1*3的矩阵）
  v =
       1     2     3
  >> v = [1;2;3]     %表示列向量（3*1的矩阵）
  v =
       1
       2
       3
  >> v = 1:0.1:2   %表示从1~2每隔0.1取数，得到的是一个行向量
  v =
    1 至 8 列
      1.0000    1.1000    1.2000    1.3000    1.4000    1.5000    1.6000    1.7000
    9 至 11 列
      1.8000    1.9000    2.0000
  >> v = 1:6       %当然也可以不取间隔
  v =
       1     2     3     4     5     6
  

• 用特殊方法建立矩阵

  >> ones(2,3)   %建立2*3的矩阵，元素全部为1
  ans =
       1     1     1
       1     1     1
  >> 2*ones(2,3)    %用2*矩阵，元素全部为2
  ans =
       2     2     2
       2     2     2
  >> zeros(2,2)    %生成零矩阵
  ans =
       0     0
       0     0
  >> rand(1,3)    %生成0~1的随机矩阵
  ans =
      0.8147    0.9058    0.1270
  >> randn(1,3)   %生成高斯分布矩阵（正态分布）均值为0，标准差为1
  ans =
      0.8622    0.3188   -1.3077
  >> >> w = -6 + sqrt(10)*(randn(1,10000)); % 生成均值为-6，方差为10的10000个数据的矩阵
  >> hist(w)     %将这个矩阵用直方图的形式画出来
  >> hist(w,50)  %用50个竖条的直方图显示
  

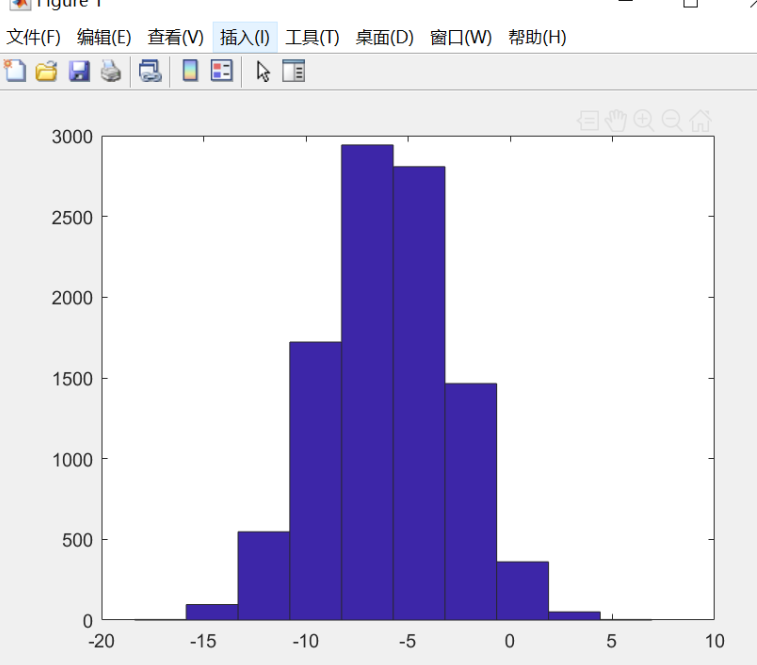
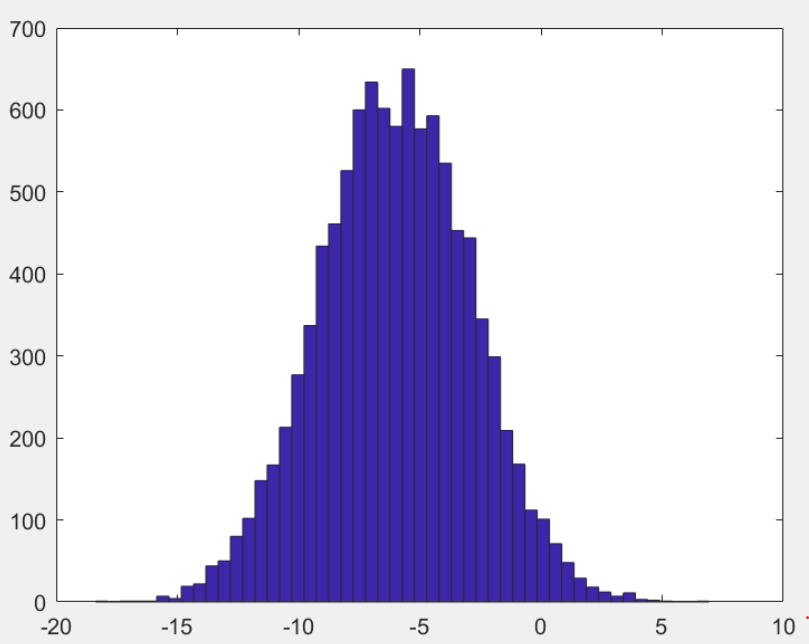
>> eye(4)   %生成单位矩阵
ans =
     1     0     0     0
     0     1     0     0
     0     0     1     0
     0     0     0     1
>> eye(3)
ans =
     1     0     0
     0     1     0
     0     0     1

2.移动数据

• 矩阵的大小

>> A = [1 2;3 4;5 6]
A =
     1     2
     3     4
     5     6
>> size(A)      %size()可以查看矩阵的大小
ans =
     3     2
>> s = size(A)   
s =
     3     2
>> size(s)        %size()本身返回的就是一个矩阵
ans =
     1     2
>> size(A,1)     %将返回A矩阵第一维度的大小（行数）
ans =
     3
>> size(A,2)     %将返回A矩阵第二维度的大小（列数）
ans =
     2
>> v = [1 2 3 4]
v =
     1     2     3     4
>> length(v)      %返回行向量的长度
ans =
     4
>> length(A)   %返回较大的维度长度3
ans =
     3

• 加载文件中的数据

  >> load('ex1data1.txt')   %使用load直接可以将文件中的数据读出来
  >> who           %显示当前工作区的变量
  
  您的变量为:
  
  A         ans       ex1data1  s         v         
  
  >> size(ex1data1)       %刚刚读的矩阵，查看长度
  ans =
      97     2
  >> whos   %查看当前工作区变量的详细信息
    Name           Size            Bytes  Class     Attributes
  
    A              3x2                48  double              
    ans            1x1                 8  double              
    ex1data1      97x2              1552  double              
    s              1x2                16  double              
    v              1x4                32  double              
  >> clear(v)   %删除变量，不加指定则删除全部变量
  >> v = ex1data1(1:10)  %取前10个元素
  v =
    1 至 8 列
      6.1101    5.5277    8.5186    7.0032    5.8598    8.3829    7.4764    8.5781
    9 至 10 列
      6.4862    5.0546
  >> save v.mat v    %将v矩阵中的数据存到文件v.mat中去
  

  • 这里存储文件时是以二进制格式存储的，因为数据量可能比较大，所以进行了压缩，如果想让人看懂存储的内容可使用下面的方法

  >> save v.txt v -ascii
  

• 操作矩阵中的数据

  >> A
  A =
       1     2
       3     4
       5     6
  >> A(3,2)  %取A矩阵中第三行第二列的元素
  ans =
       6
  >> A(2,:)   %取A矩阵中第二行的所有元素
  ans =
       3     4
  >> A(:,2)   %取第二列的所有元素
  ans =
       2
       4
       6
  >> A([1 3],:)    %取A矩阵第一行和第三行的所有元素
  ans =
       1     2
       5     6
  >> A(:,2) = [10 15 20]  %取出元素之后其实可以对其进行赋值
  A =
       1    10
       3    15
       5    20
  >> A = [A,[100;150;200]] %在A矩阵后面追加一列
  A =
       1    10   100
       3    15   150
       5    20   200
  >> A(:)    %把A矩阵的所有元素放到一个列向量中
  ans =
       1
       3
       5
      10
      15
      20
     100
     150
     200
  >> A = [1 2;3 4;5 6];
  >> B = [11 12;13 14;15 16];
  >> C = [A,B]     %将两个矩阵拼接到一起
  C =
       1     2    11    12
       3     4    13    14
       5     6    15    16
  >> C = [A;B]      %分号表示换行，B矩阵放在A矩阵的下面
  C =
       1     2
       3     4
       5     6
      11    12
      13    14
      15    16
  

3.计算数据

• 矩阵之间的运算

  >> A = [1 2;3 4;5 6];
  >> B = [11 12;13 14;15 16];
  >> C = [1 1;2 2]
  C =
       1     1
       2     2
  >> A * C     %A与C进行矩阵相乘
  ans =
       5     5
      11    11
      17    17 
  >> A .* B      %'.*'代表矩阵中对应元素相乘
  ans =
      11    24
      39    56
      75    96
  >> A .^ 2     %'.'代表对矩阵中的所有元素，乘方
  ans =
       1     4
       9    16
      25    36
  >> v = [1 2 3] 
  >> v = 1 ./ v    %取v矩阵的倒数
  v =
      1.0000    0.5000    0.3333
  >> log(v)     %对v取log运算
  ans =
           0   -0.6931   -1.0986
  >> exp(v)      %对v取e^v次方运算
  ans =
      2.7183    1.6487    1.3956
  >> abs([-1;-2;3])  %对矩阵取绝对值运算
  ans =
       1
       2
       3
  >> -v          %对矩阵取相反数
  ans =
     -1.0000   -0.5000   -0.3333
  >> v = [1;2;3];
  >> v = v + ones(length(v),1) %将v中所有元素+1，先构造一个和v维度相同的矩阵（元素全为1），再把他们相加
  v =
       2
       3
       4
  >> v = v +1     %实际上用+号就可以实现
  v =
       3
       4
       5
  >> A'      %一个撇号是求矩阵的转置
  ans =
       1     3     5
       2     4     6
  

• 对矩阵的函数操作

  >> a = [-0.2 9.8 4.5 8 2.0]
  a =
     -0.2000    9.8000    4.5000    8.0000    2.0000
  >> val = max(a)   %求矩阵的最大值
  val =
      9.8000 
  >> [val index] = max(a)    %求矩阵的最大值并返回他的下标索引
  val =
      9.8000
  index =
       2
  >> a < 3     %拿a中的所有元素和3比较返回结果
  ans =
    1×5 logical 数组
     1   0   0   0   1
  >> find(a<3)   %返回满足条件的元素在a中的索引
  ans =
       1     5
  >>A = magic(3)  %幻方矩阵，每一行每一列包括对角线元素之和相等
   A =
       8     1     6
       3     5     7
       4     9     2
  >> [r,c] = find(A>=7)  %寻找A中大于等于7的元素索引，行和列
  r =
       1
       3
       2
  c =
       1
       2
       3
  >> sum(a)    %对矩阵中的元素求和
  ans =
     24.1000
  >> prod(a)    %对矩阵中的元素相乘
  ans =
   -141.1200
  >> floor(a)    %向下取整
  ans =
      -1     9     4     8     2
  >> ceil(a)      %向上取整
  ans =
       0    10     5     8     2
  >> A
  A =
       8     1     6
       3     5     7
       4     9     2
  >> max(A,[],1)   %取每一列的最大值，1代表是第一维度
  ans =
       8     9     7
  >> max(A,[],2)   %取每一行的最大值
  ans =
       8
       7
       9
  >> max(max(A))  %取A矩阵所有元素的最大值
  ans =
       9
  >> max(A(:))  %或者先将矩阵A转化为列向量，在取最大值
  ans =
       9
  >> sum(A,1)  %求A每一列的和
  ans =
      15    15    15
  >> sum(A,2) %求A每一行的和
  ans =
      15
      15
      15
  >> A .* eye(3)   %将单位矩阵与A中的元素相乘得到对角线的元素
  ans =
       8     0     0
       0     5     0
       0     0     2
  >> sum(sum(A .* eye(3)))  %求对角线元素的和
  ans =
      15
  >> pinv(A)    %求逆矩阵
  ans =
      0.1472   -0.1444    0.0639
     -0.0611    0.0222    0.1056
     -0.0194    0.1889   -0.1028
  >> temp = pinv(A);
  >> A*temp     %发现这就是单位矩阵
  ans =
      1.0000   -0.0000    0.0000
      0.0000    1.0000   -0.0000
     -0.0000    0.0000    1.0000
  

4.数据绘制

• 有时需要绘制数据的图像以便更好地观察我们的算法是否出现错误，或者更好的检验我们的想法的正确性，我们需要将数据可视化，这点很重要。

  >> t = [0:0.01:0.98]; 
  >> y1 = sin(2*pi*4*t);
  >> plot(t,y1);   %用plot就可以画出对应的sin函数图像
  >> y2 = cos(2*pi*4*t);
  >> hold on;     %在同一界面上画图像
  >> plot(t,y2,'r');   %画出cos的函数图像，用red
  >> xlabel('time');    %设置x轴坐标
  >> ylabel('value');   %设置y轴坐标
  >> legend('sin','cos');  %设置标识
  >> title('my plot');   %设置标题
  >> print -dpng 'myplot.PNG';  %将图像保存为PNG格式
  

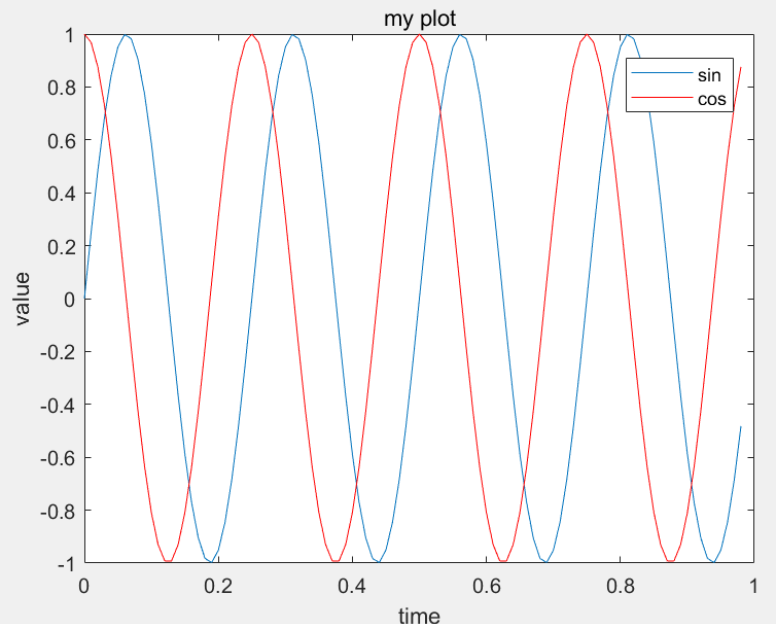
>> figure(1); plot(t,y1);  %对图像进行标号这样每个图象一个界面
>> figure(2); plot(t,y2);
>> subplot(1,2,1);    %将界面分为1*2的区域，用第一块区域
>> plot(t,y1);     %第一块区域画y1的图像
>> subplot(1,2,2);    %用第二块区域
>> plot(t,y2);      %第二块区域画y2的图像
>> axis([0.5 1 -1 1]);   %设置图像的横纵坐标范围

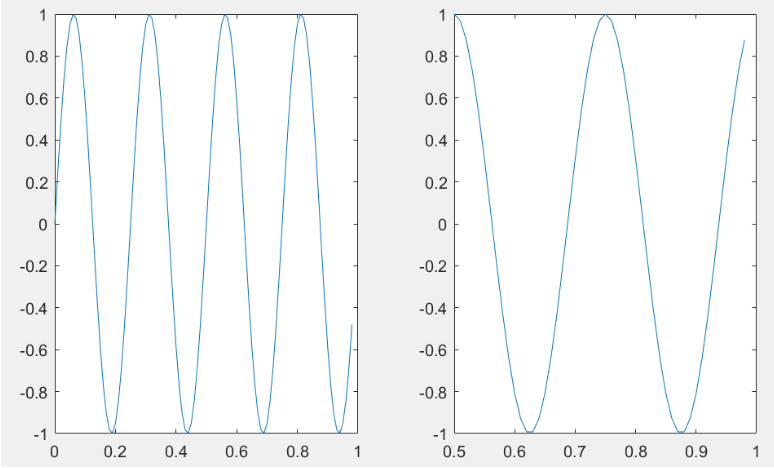
>> A = magic(5)  %5*5的幻方矩阵
A =
    17    24     1     8    15
    23     5     7    14    16
     4     6    13    20    22
    10    12    19    21     3
    11    18    25     2     9
>> imagesc(A);   %矩阵也可以可视化

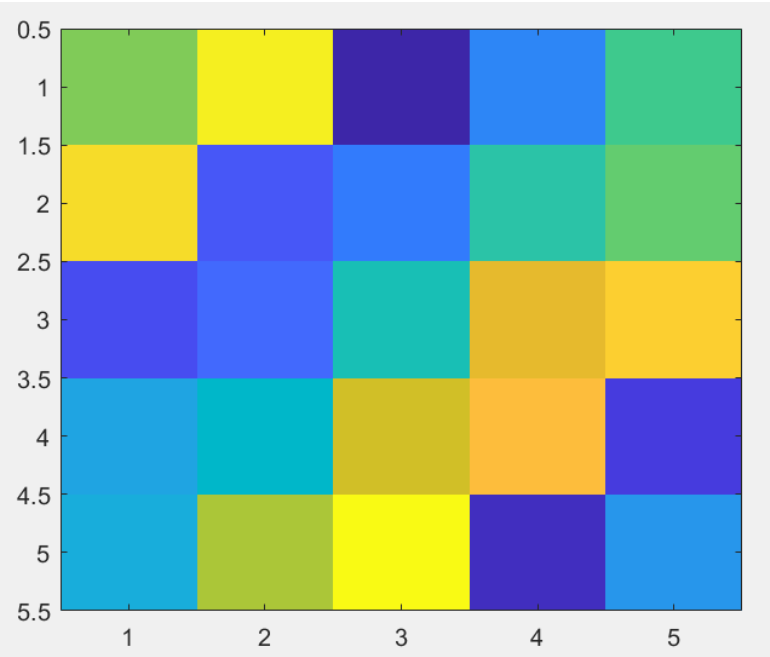
>> imagesc(A),colorbar,colormap gray; %执行了三个命令，用有灰度的图像来画矩阵，并显示灰度表

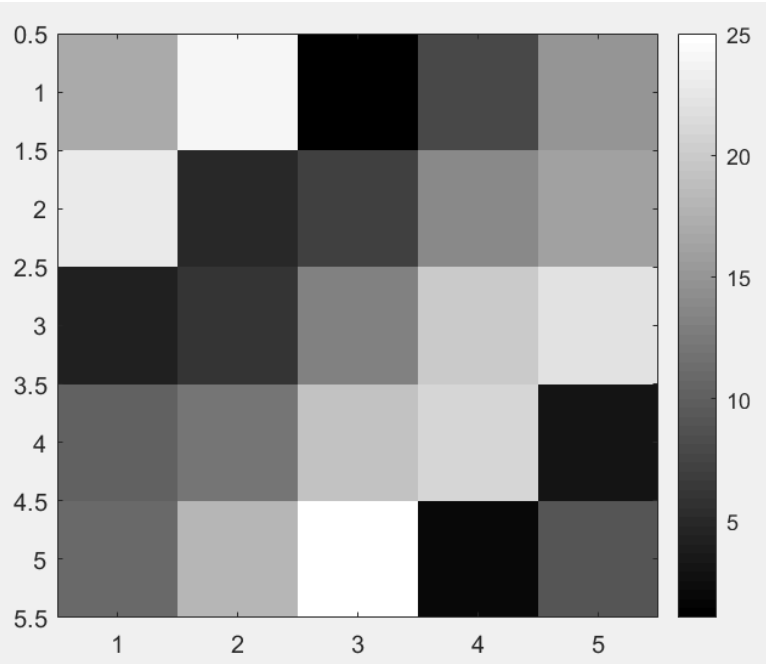
>> imagesc(magic(15)),colorbar,colormap gray;%打印15*15的幻方矩阵

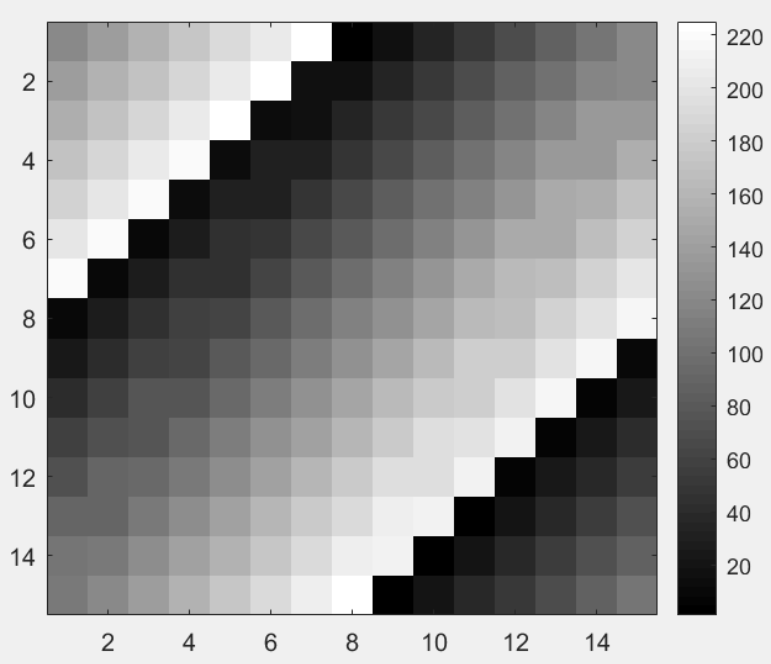
5.控制语句：if，for，while语句

>> v = zeros(10,1)
>> for i = 1:10,  %i = 1:10,之后把v(i)的值变为2的i次方
     v(i) = 2^i;
   end            %注意结束的时候加上end
>> v
v =
           2
           4
           8
          16
          32
          64
         128
         256
         512
        1024
>> i = 1;
>> while true,    %while循环
     v(i) = 999;  %设置v(i)的值为999
     i = i + 1;
     if i == 6,  %当i=6时跳出循环
        break;
     end
  end
>> v
v =
         999
         999
         999
         999
         999
          64
         128
         256
         512
        1024

• 定义函数

  创建一个sqrt_test.m文件，在里面输入以下内容：

  function y = sqrt_test(x) %y是返回值，x为传入的参数
      y = x^2
  end
  

  之后在控制台中cd 到文件所处目录，调这个函数执行命令

  >> sqrt_test(5);
  y =
      25
  

  matlab的函数还可以有多个返回值，比如将上面的函数改一下：

  function [a,b] = sqrt_test(x)
      a = x^2
      b = x^3
  end
  

  >> [a,b] = sqrt_test(5);
  a =
      25
  b =
     125
  

• 下面用matlab实现代价函数的定义，并且用简单的数据集检验是否正确，数据集如下：
  

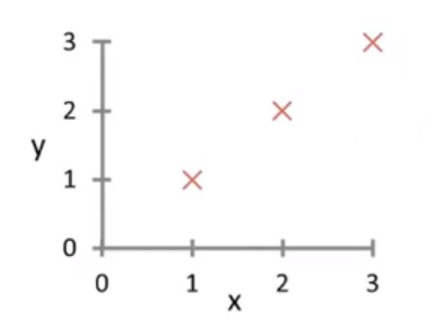
  我们定义的代价函数如下：

  function J = costFunctionJ(X,y,theta)
      m = size(X,1);       %数据集的个数
      predictions = X*theta;    %假设函数预测的结果矩阵
      sqrErrors = (predictions - y) .^ 2;   %与实际值得误差
      J = 1/(2*m) * sum(sqrErrors);     %计算代价函数
  end
  

  下面我们在终端中调用这个函数：

  >> X = [1 1;1 2;1 3];
  >> Y = [1;2;3];
  >> X
  X =
       1     1
       1     2
       1     3
  >> Y
  Y =
       1
       2
       3
  >> theta = [0;1]
  theta =
       0
       1
  >> costFunctionJ(X,Y,theta)  %theta0=0,theta0=1刚好拟合，故代价函数为0
  ans =
       0
  >> theta = [0;0]
  theta =
       0
       0
  >> costFunctionJ(X,Y,theta)
  ans =
      2.3333
  

6.向量化

• 下面通过几个例子来说明向量化的代码会更加简单明了。

• 首先我们先写一个计算假设函数的function，前面我们已经知道假设函数的公式如下：
  $$h(x)=\sum _{j=1}^n{\theta }_j{x}_j$$
  那么正常来写求假设函数的matlab代码就是：

  function pre = prediction(X,theta)
      pre = 0.0;
      n = size(X,1);
      for j = 1:n,
          pre = pre + theta(j) * X(j)
      end;
  end
  

  而我么前面也推到过，假设函数还可以写成向量的形式：
  $$\begin{gathered} h(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdot \cdot \cdot +{\theta }_n{x}_n=[{\theta }_0,{\theta }_1,\cdot \cdot \cdot {\theta }_n]\ast \left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ \cdot \cdot \cdot \\ x_n\end{array}\right] \\ ={\theta }^{T}X \end{gathered}$$
  这样我们的函数就可以使用matlab提供的线性代数库来求解了，可以大大减少代码量：

  function pre = prediction(X,theta)
     pre = theta' * X;  % ' 代表矩阵的转置
  end
  

• 再比如说我们前面所讨论的的梯度下降的更新公式：
  $${\theta }_n={\theta }_n-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x_i)-y_i)x_n^{(i)}$$
  这里我们也是假设θ为一个列向量，那么更新之后的θ就等于原来的列向量θ 减去 a/m（实数）* （（h(x)(假设函数列向量) - y（数据集y列向量））*X（特征值矩阵））

  下面是更新theta值的matlab代码：

  function Theta = UpdateTheta(X,Y,theta,alpha)
      m = size(X,1);
      Error = X * theta - Y;
      deta = alpha/m * (X' * Error);
      Theta = theta - deta;
  end
  

  由此可见，使用向量化可以使代码大大减小，相对于之前写的python实现更加简单，并且对于特征值较多的也可以避免使用for循环，使用矩阵运算还可以提高运算速度。

最后

以上就是如意灰狼为你收集整理的Machine Learning 学习笔记(四)———Matlab基础教程的全部内容，希望文章能够帮你解决Machine Learning 学习笔记(四)———Matlab基础教程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。