
在上一篇中,我们学习到了计算机底层的一些机器码,以及一些行业标准,这一章,我们将接着学习机器码的一些比较与相关计算。
一、浮点数表示和定点数的比较
① 当字长相同时,浮点数表示的范围要大得多。
②浮点数表示比定点数表示的分辨率高。
③浮点数表示比定点数表示的应用范围更广。
④ 浮点数表示比定点数表示复杂、运算步骤多、硬件实现也复杂得多。
⑤ 浮点数表示和定点数表示判断溢出的方法不同。
二、补码的加减运算及溢出判断
1. 补码加法运算
补码加法的公式为:
公式说明,两个带符号的补码可以直接相加,和就是两个数和的补码,这一公式也适用于定点小数的补码加法运算。
对不同字长的数运算,要先变成相同字长的数,(以字长比较长的数为标准)
操作码为“加”时,两数直接相加。
2. 补码减法运算
根据补码加法运算的公式很容易得出补码减法运算的公式:
公式说明,求两个数差的补码,可以用被减数的补码加上和减数符号相反数的补码实现。这样,采用补码运算,就可以化减为加,计算机的运算器中只需要设计加法器,减法器就不需要了。
操作码为“减”时,将减转换为加,即将减数变补后与被减数相加。

例: 求(X – Y)补
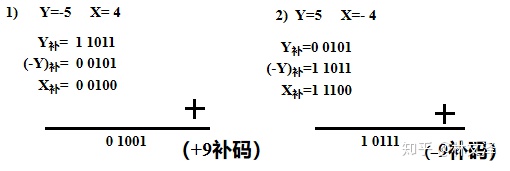
3. 溢出判断
当运算结果超出数的表示范围,就会发生溢出
在做加法和减法运算时,有四种可能:
- 同号相加
- 异号相减
- 同号相减
- 异号相加
机器是如何判断溢出的?
- 符号位和进位位判断
- 双符号位判断
三、移位运算
算术移位是指有符号数的移位,主要用于乘除运算。算术左移相当于乘以2,右移相当于除以2
1. 原码移位
- 原码移位规则:符号位不参加移位
- 左移:数值位高位移出,末位补0(高位为1时,左移会丢失高位出错)
- 右移:数值位低位移出,高位补0(末位为1时,右移会损失数的精度)
2. 补码移位
- 补码移位规则:符号位参加移位
- 左移:数值位高位移至符号位,符号位移出,末位补0 (高位为1时,符号位为0,左移改变符号位,并丢失高位出错)
- 右移:数值位低位移出,符号位不变(末位为1时,右移会损失数的精度)
3. 逻辑移位
逻辑移位是指无符号数的移位,可用于实现数的串行和并行之间的转换等功能。逻辑移位有左移、右移、循环左移和循环右移等几种。
3.1 左移右移
- 左移:数值位高位移出,末位补0
- 右移:数值位低位移出,高位补0
3.2 循环左移右移
- 循环左移:数值位高位移至末位
- 循环右移:数值位低位移至高位
例: X = 11010101,Y = 00101010,将X 和Y循环左移两位。
X = 01010111,Y = 10101000
最后
以上就是殷勤夕阳最近收集整理的关于左移和右移的运算规则_计算机硬件技术基础M2——计算机运算基础(二)的全部内容,更多相关左移和右移内容请搜索靠谱客的其他文章。


![[计算机组成原理]2-6、算数移位、逻辑移位、循环移位](https://www.shuijiaxian.com/files_image/reation/bcimg6.png)





发表评论 取消回复