先导-逻辑图的表示
1.与或非
01
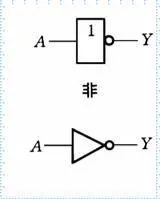
02
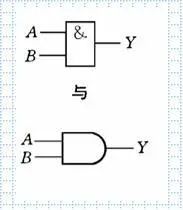
03
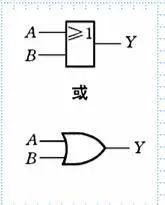
2.扩展,异或(不同为1,相同为0)和同或(相同为1,不同为0)
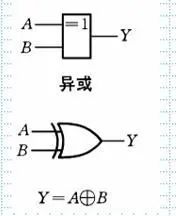
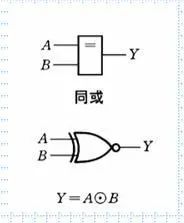
3.复合运算
与非,与后面加一个小圆圈
或非,或后面加一个小圆圈
与或非,两个与输入到或中,或后面加一个小圆圈
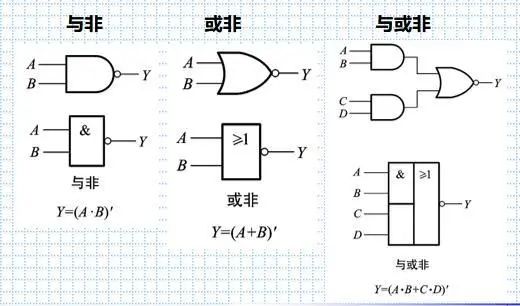





4.逻辑公式,基本和导出
注意与非和或非的运算!!!!!

逻辑公式的进一步扩展--代入定理
------在任意一个包含变量A的等式中,若用任何一个逻辑式代替等式中的A,则等式仍然成立。
5.逻辑函数及其表示方法
•真值表
输入变量所有可能的取值和输出对应的取值
标准形式:最小项之和
最小项的 •m是乘积项 •包含n个输入变量 •n个输入变量都以原变量或反变量的形式在m中出现一次
•逻辑式
(1)将逻辑函数的输出写成输入逻辑变量的代数运算式
(2)表示方法:最小项 m
(3)最小项的定义:
•m是乘积项
•包含n个输入变量
•n个输入变量都以原变量或反变量的形式在m中出现一次
(4)补充且n个变量有2的n次方个最小项,每个最小项还有对应编号。为非时取0,本身时取1,写出对应二进制数即为编号
(5)最小项的特点
•在输入变量的任何取值下,必有一个、而且仅有一个最小项取值为1。
•全部最小项之和为1 。
•任意两个最小项之积为0 。
•具有相邻性的两个最小项之和可以合并为一项,合并后的结果中只保留这两项的公共因子。
------相邻性:两个最小项之间仅有一个变量不同
•逻辑图 来描述逻辑函数
用逻辑图形符号连接起来表示逻辑函数,得到的连接图称为逻辑图。注意分析输入端即可,还有分清楚逻辑符号。
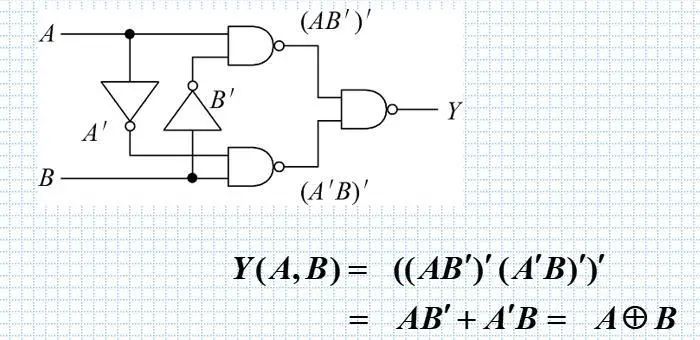
•波形图
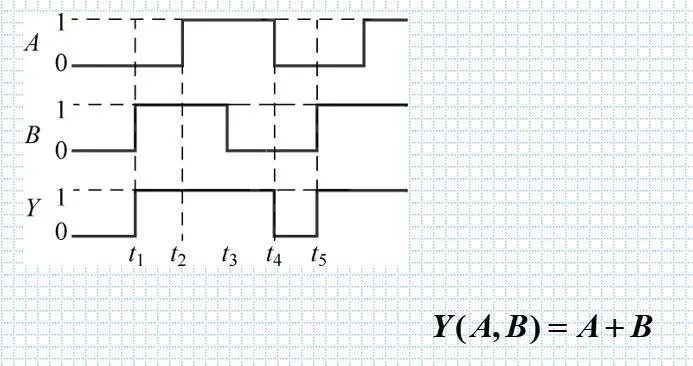
将输入变量所有可能的取值与对应的输出按时间顺序依次排列起来画成的时间波形,称为函数的波形图。
因为输入AB默认是00,01,11,10变化,对应画出输出即可。
•卡诺图
(1)最小项的卡诺图表示法
• •实质:将逻辑函数式的最小项之和形式以图形的方式表示出来。
• • •以2n个小方块分别代表 n 变量的所有最小项,并将它们排列成矩阵,而且使几何位置相邻的两个最小项在逻辑上也是相邻的(即只有一个变量不同),就得到了表示n变量全部最小项的卡诺图。
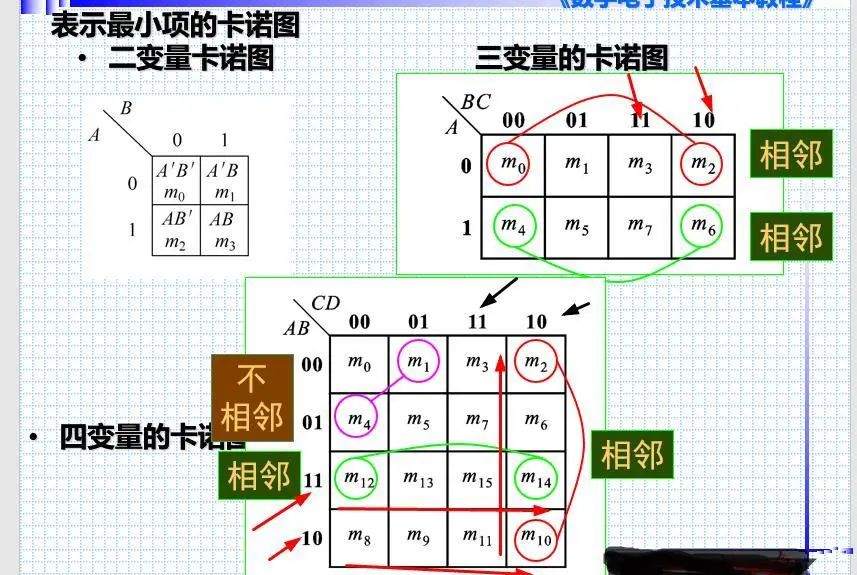
(2)表示逻辑函数的步骤
•将函数表示为最小项之和的形式
• 在最小项的卡诺图上与函数式中包含的最小项所对应位置上填入1,在其余的位置上填入0。
•硬件描述语言(略,详细见实验课)
6.各种表示方法之间可以相互转换
(1)真值表 和逻辑式:
从真值表中找出所有使函数值等于1 的输入变量取值。
上述的每一组变量取值下,都会使一个乘积项的值为1。在这个乘积项中,取值为1的变量写入原变量,取值为0的写入反变量。
将这些乘积量相加,就得到了所求的逻辑函数式。
而真值表,只要根据变量数,按照二进制数的写法,从小到大不遗漏写出即可。
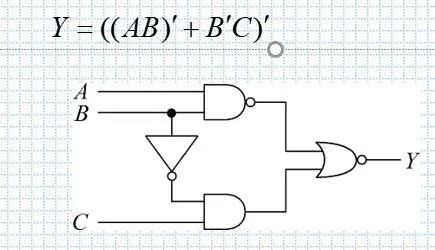
(2)逻辑式和逻辑图
用图形符号代替逻辑式中的代数运算符号,并依照逻辑式中的运算优先顺序将这些图形符号连接起来。
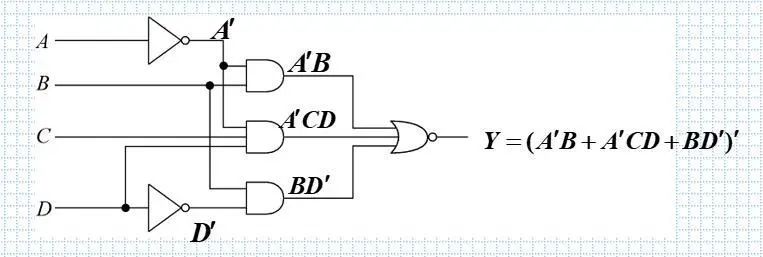
如果给出逻辑图,则只要从输入端到输出端写出每个图形符号所表示的逻辑运算式。
理解:画逻辑图一步一步组合,可以从最后看是什么,再推到前面,输入三个端口,到最后一个输出。写逻辑式就是分析输入端的是什么,输出效果是怎么样的
(3)逻辑式和卡诺图
1. 将给定的逻辑函数式表示为卡诺图。化为最小项之和,写在卡诺图上即可。
2. 如果给出了卡诺图,则只要将卡诺图中填入1的位置上的那些最小项相加即可。
比如: 与或式到卡诺图:把每一个乘积项所包含的那些最小项(该乘积项就是这些最小项的的公因子)所对应的小方块都填上1,剩下的填0,就可以得到逻辑函数的卡诺图。
(4)波形图 到真值表
1. 按给出的函数真值表,画出波形图。
依次画出即可
2. 如果给出了函数的波形图,则需要将每个时间段的输 入与输出的取值列表。分变量取值。
7.逻辑函数的化简方法
(1)逻辑函数的最简形式----最简与或
使函数式中所包含的乘积项最少,同时每个乘积项所包含的因子最少,称为最简的与或逻辑式。
举例
(1) 公式化简法
•利用逻辑代数的基本公式和常用公式对逻辑代数式进行运算,消去式中多余的乘积项和每个乘积项中多余的因子。
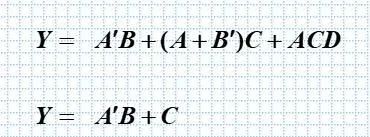
思路是采用本身 加 非为1
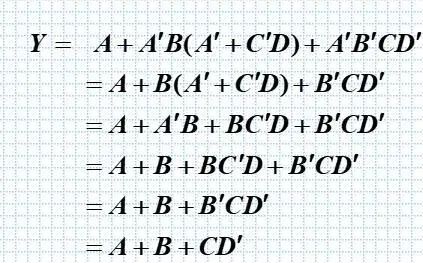
思路为合并。

思路是分开增加项数

用了对应公式,消去项
(2)卡诺图化简
2.1.依据:具有相邻性的最小项可合并,消去不同因子。
在卡诺图中,最小项的相邻性可以从图形中直观地反映出来。
2.2 合并最小项的原则:
– –两个相邻最小项可合并为一项,消去一对因子
– –四个排成矩形的相邻最小项可合并为一项,消去两对因子
– –八个排成矩形的相邻最小项可合并为一项,消去三对因子
注意最左和最右,最上和最下都是相邻的,四个角也是。对于四个变量的卡诺图。
2.3.化简步骤
(1)用卡诺图表示逻辑函数
(2)将卡诺图中按矩形排列的相邻的1圈成若干个相邻
组,原则是:
•这些相邻组必须覆盖卡诺图上所有的1。
•每个相邻组中至少有一个1不包含在其他相邻组内。
•相邻组的数目应最少。
•每个相邻组应包含尽可能多的1。
(3)化简后的乘积项相加
2.4.逆向化简
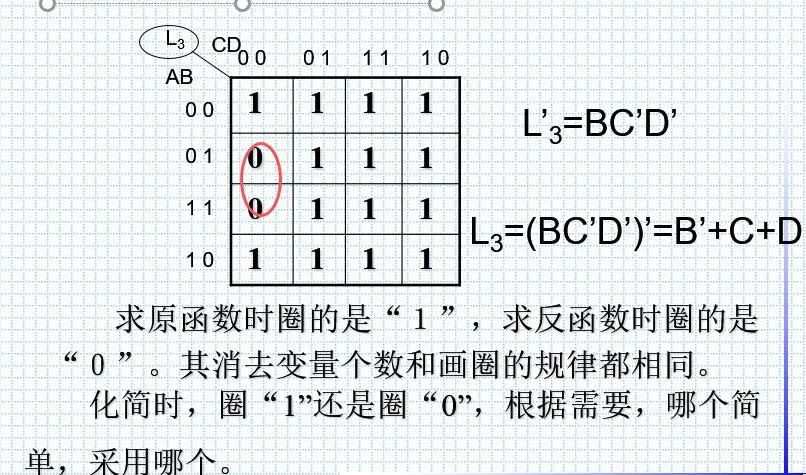
8.逻辑函数中的无关项的化简
(1)无关项:约束项和任意项可以写入函数式,也可不包含在函数式中。
···约束项:输入变量的某些取值在工作过程中始终不会出现,对于这些输入变量取值下等于1的最小项
···任意项:输入变量的某些取值下,输出是1、是0均可,是任意的。在这些输入变量下取值为1的最小项
例:当8421BCD码作为输入变量时,禁止码1010~1111这六种状态所对应的最小项就是无关项。
(2)如何化简
•加入(或去掉)无关项,应使化简后的项数最少,每项因子最少······
··从卡诺图上直观地看,加入无关项的目的是为了使矩形圈最大,矩形组合数最少。
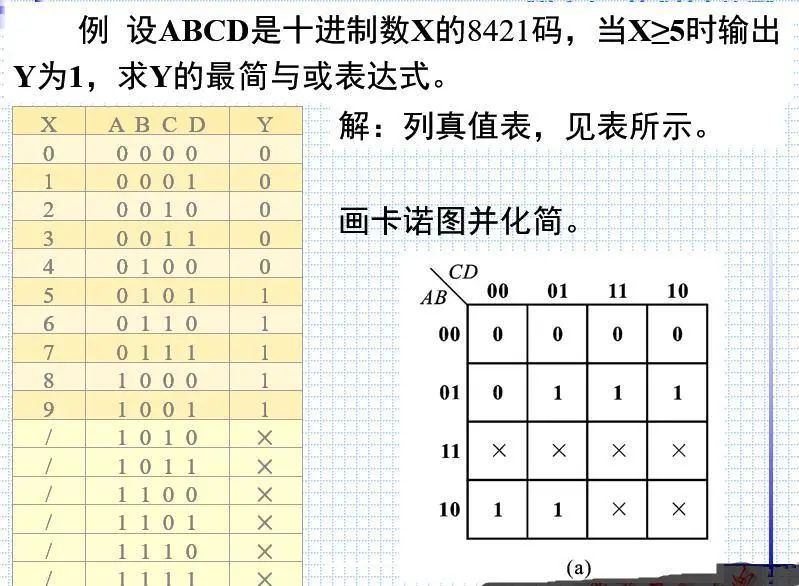
注意:无关项可以当作1来看,但画出的圈不能只有无关项,要有一般项。
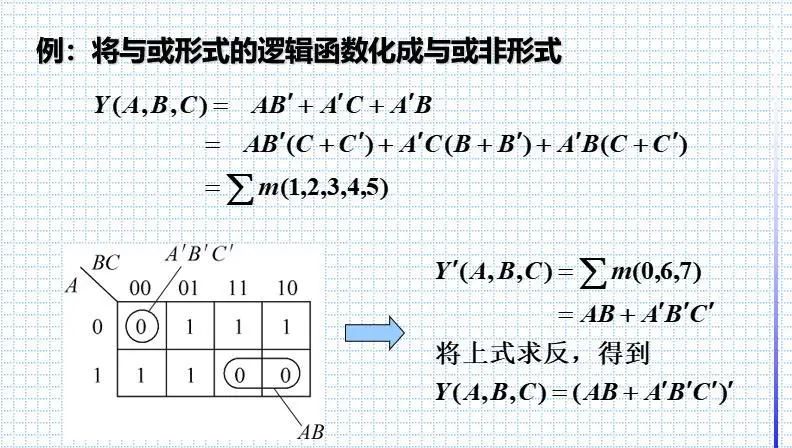
9.逻辑函数形式的变换
与或和与非
通过公式 与非=非或
或非=非与实现。
二极管构成的电路

与门电路
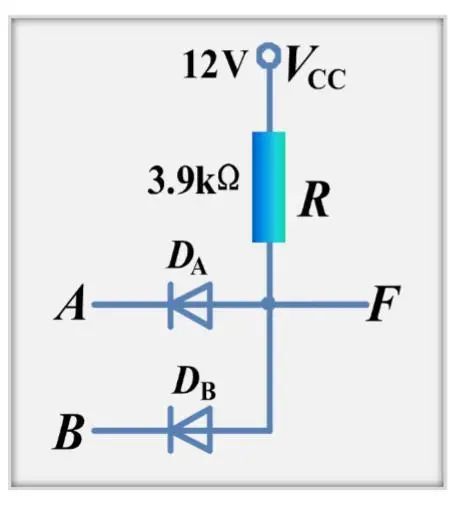
分析:二极管导通时,电势差为0.7
A低B低,Da导通,Db导通 ,F为0,.7v,低
A高B低,Db比Da优先导通,故Da截止,Db导通,F为0.7v,低
A低B高,Da比Db优先导通,故Da导通,Db截止,F为0.7v,低
A高B高,Da导通,Db导通,F为高
2.或门
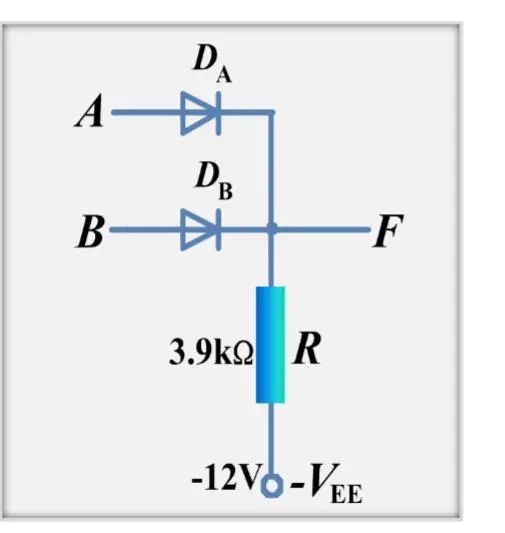
A低B低 ,Da,Db导通,F为低
A高B高,Da,Db导通,F为高
A高B低,Da先于Db导通,Da导通,Db截止,F为高
B高BA低,Db先于Da导通,Db导通,Da截止,F为高
MOS管介绍和电路

N沟道增强型MOS管
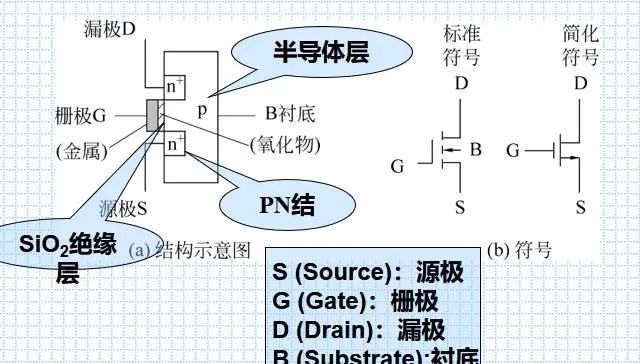
(1) VIL=0时,D-S间不导通,MOS管截止,ROFF非常大,开关断开
(2) 加上足够高的+VIH,且>VT, D-S间形成n型导电沟道,MOS管导通, ROFF<1KΩ,开关接通, D-S间相当于是一个受VI控制的开关。
我的理解:n沟道增强型mos管形成n型导电沟道,加正向电压,吸引电子过来,进而形成。
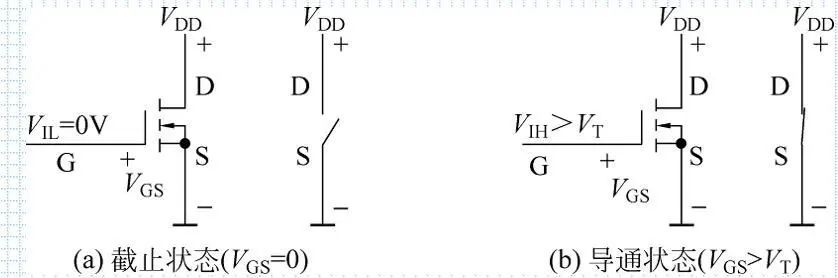
2.p沟道增强型MOS管
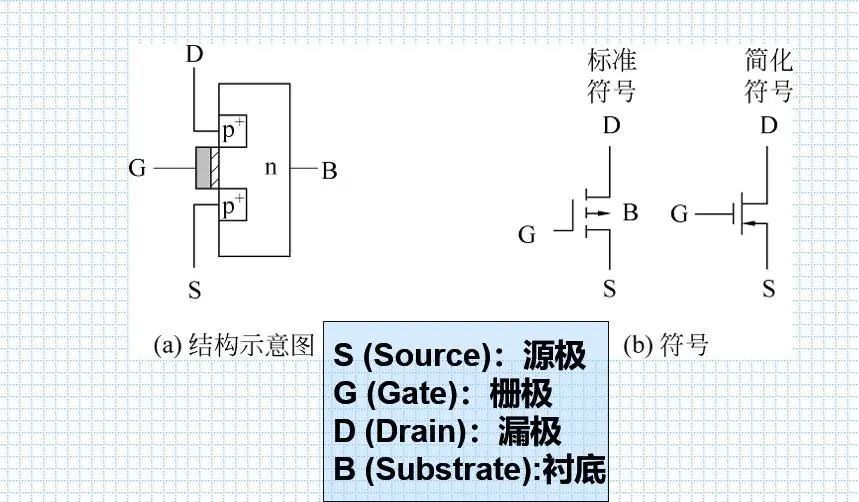
P沟道增强型MOS管的开关状态
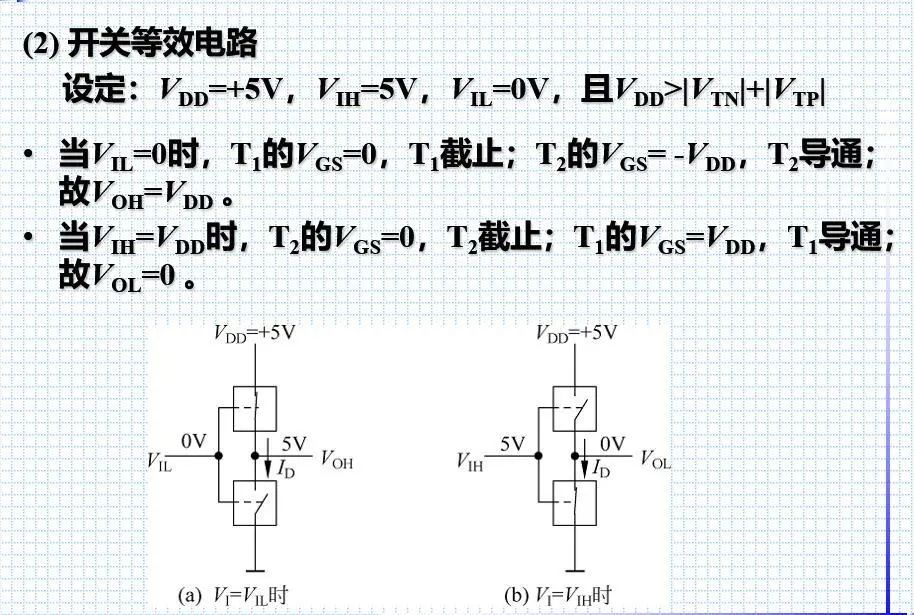
(1) VIH=VDD时, VGS=0,S-D间不导通,MOS管截止
(2) VIL=0时,VGS=-VDD,且VDD>|VT|,S-D间形成p型导电沟道,MOS管导通, S-D之间也构成一个受VI控制的开关。
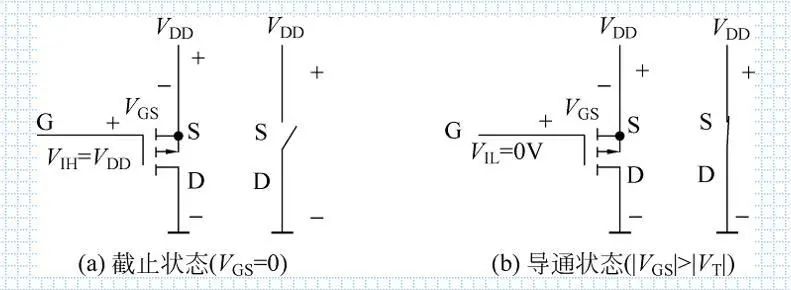
我的理解:加正电压,排斥带正电的空穴,只有加低电压,形成一个负电压,吸引空穴,从而形成p型导电沟道。
3,区分 于耗尽型,不做过多了解
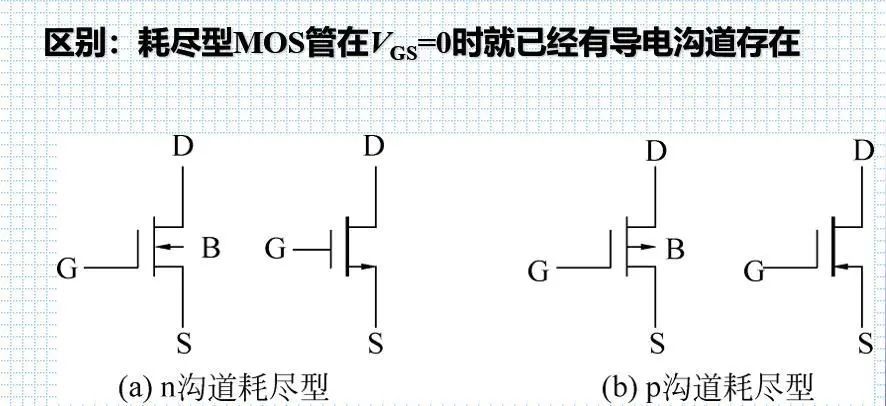
4.反相器 ----相当于逻辑非
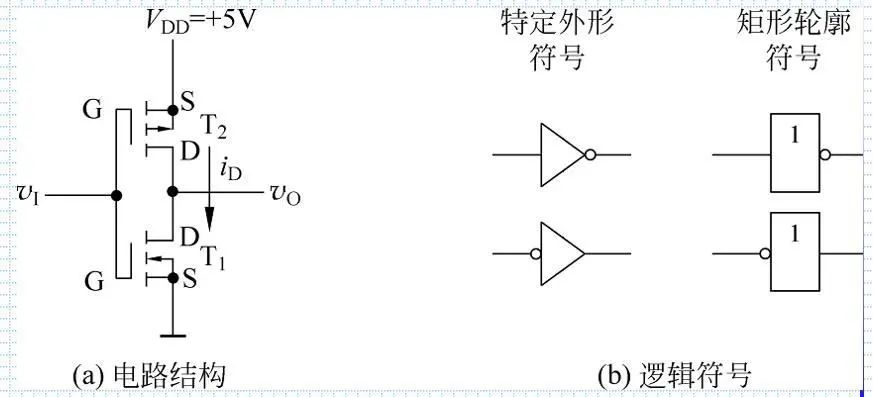
上面是一个p沟道增强型,下面是一个n沟道增强型。
v1为高,T2截止,T1导通即D,S导通,S接地,输出为低
V1为低,T1截止,T2导通即D,S导通,S接高电压,则输出为高。
符号类似非
5,CMOS传输门--由信号控制门的开关
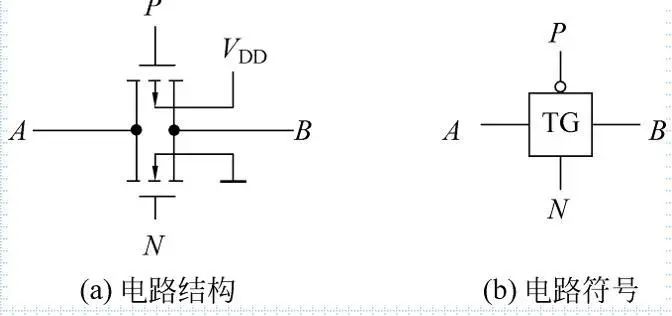
上面是p沟道增强型MOS管,下面是n沟道增强型
p高n低,p,n截止,A,B断开
P低n高,p,n导通,A,B导通

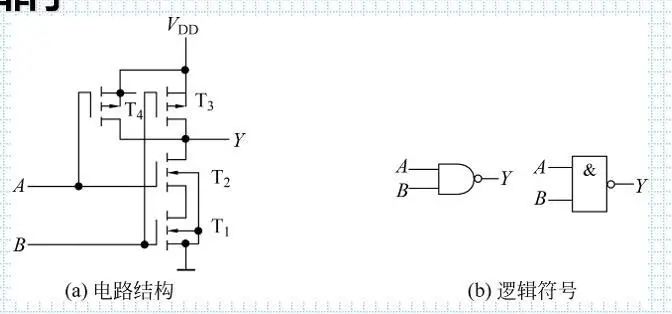
6.进阶电路之与非门
T1,T2为n沟道增强型MOS管
T3,T4为p沟道增强型MOS管
其中A输入到T2和T4,B输入到T2和T3
A低B高,T2截止,T4导通,T1导通,T3截止,则Y为高
A低B低,T2截止,T4导通,T1截止,T3导通,则Y为高
A高B高 ,T2导通,T4截止,T1导通,T3截止,因为T3和T4都截止,则Y为低
A高B低,T2导通,T4截止,T1截止,T3导通,则Y为高。
7.进阶电路之或非门
T1,T2是n沟道增强型,T3和T4是p沟道增强型,而A接的是T2和T4,B接的是T1和T3,
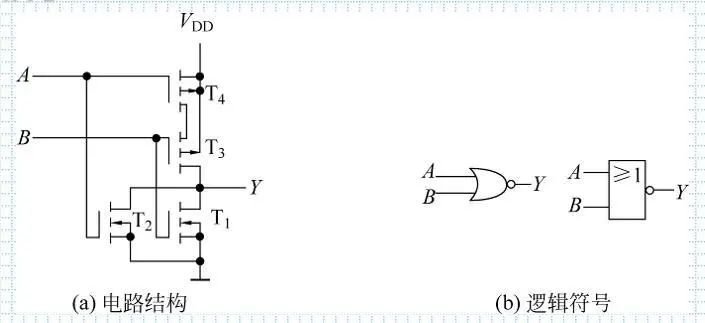
同理去分析,
A高B高,T2导通,T4截止,T3截止,T1导通,Y接地,为低
A低B低,T2截止,T4导通,T3导通,T1截止,Y为高
A低B高,T2截止,T4导通,T3截止,T1导通,Y接地,为低
A高B低,T2导通,T4截止,T3导通,T1截止,Y接地,为低
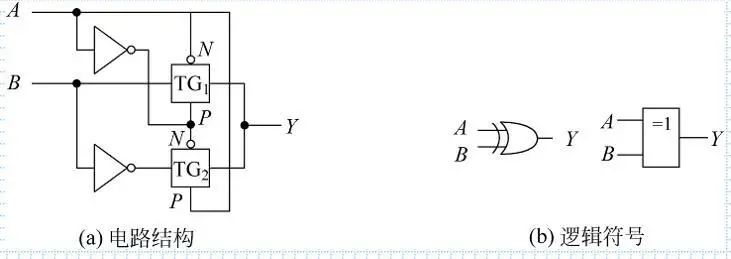
8.进阶电路 异或门
两个逻辑非,和连通器
当P低N高时导通
两个导通状态相反
且A输入信号控制导通状态,B控制输入输出
A低B低,TG1的N低P高,截止,TG2N 的高P低,导通,输出Y为高
A低B高,TG1的N低P高,截止,TG2的N高P低,导通,输出为低
A高B低,TG1的N高P低,导通,TG2的N低P高,截止,输出为低
A高B高,TG1的N高P低,导通,TG2的N低P高,截止,输出为高
9.异或非
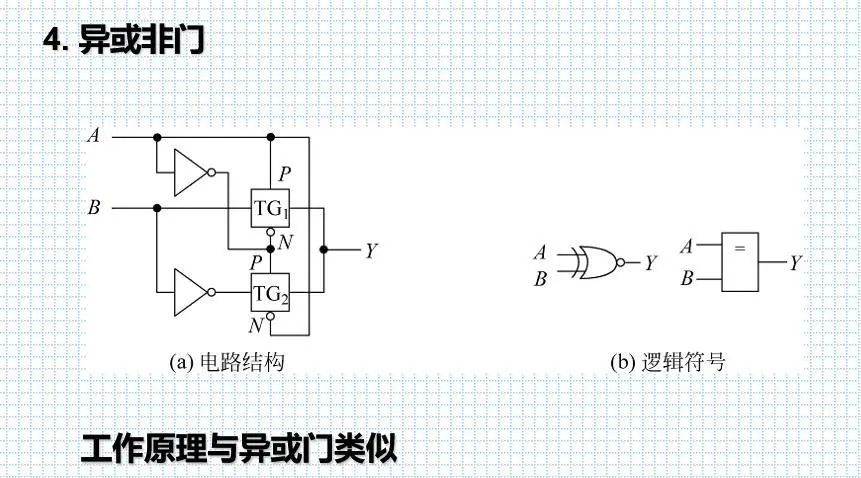
较上面把PN交换了
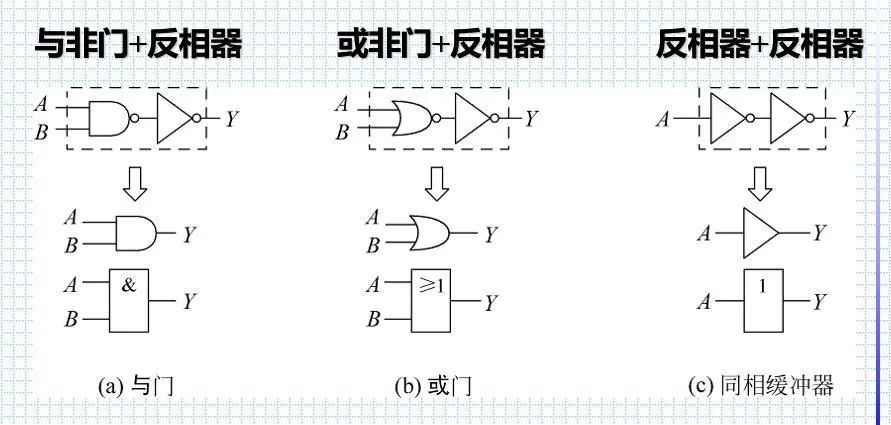
10.由反相器、传输门、与非门、或非门可以组成其他逻辑功能的门电路或逻辑电路。
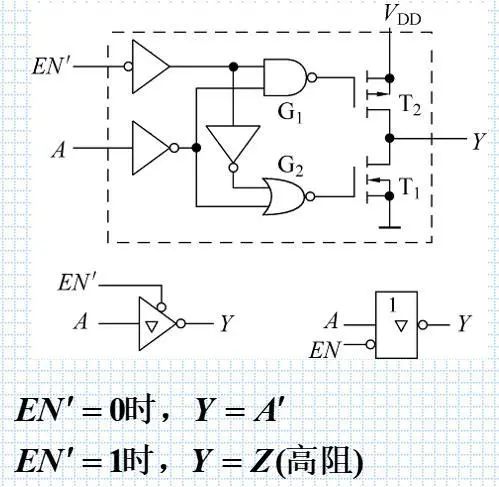
11.三态输出电路
THE END
最后
以上就是高挑帅哥最近收集整理的关于逻辑电路波形图怎么画_数电学习之 逻辑电路(1)的全部内容,更多相关逻辑电路波形图怎么画_数电学习之内容请搜索靠谱客的其他文章。








发表评论 取消回复