本章主要介绍时序逻辑电路的工作原理 、 分析方法及设计方法 。

• 首先讲述时序逻辑电路的功能及结构特点 、 分析方法和步骤
• 然后具体介绍寄存器 、 计数器等各类时序逻辑电路的工作原理和使用方法
• 最后介绍时序逻辑电路的设计方法 。

本章重点是计数器的分析和设计

1.定义

• 时序逻辑电路：在任意时刻的输出信号不仅取决于当时的输入信号，而且还取决于电路原来的状态

2. 时序逻辑电路的构成和结构特点

1. 时序逻辑电路包含组合逻辑电路和存储电路两个部分
2. 存储电路的输出状态必须反馈到组合电路的输入端，与输入信号一起，共同决定组合逻辑电路的输出
   结构如下图所示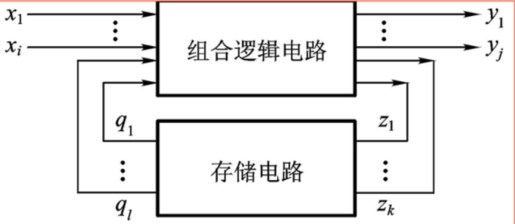
3. 可以用三个方程组来描述

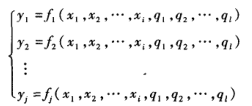
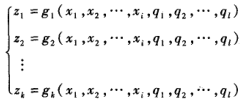
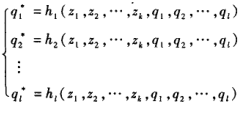
$q_1,q_2...$是指触发器的现状，$q_1\ast ,q_2\ast ...$是指触发器的次态

2.1 例子

串行加法器电路如图所示，写出其输出方程、驱动方程和状态方程

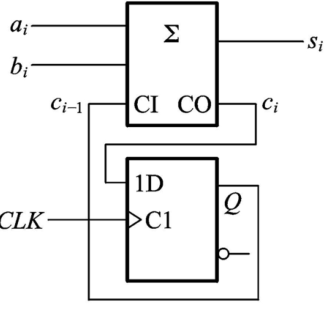
输出方程：
$s_i=a_i\oplus b_i\oplus C_{i-1}=a_i\oplus b_i\oplus Q$
驱动方程：
$D=C_i=a_i{b}_i+C_{i-1}(a_i\oplus b_i)=a_i{b}_i+Q(a_i\oplus b_i)$
状态方程：
$Q\ast =D=a_i{b}_i+Q(a_i\oplus b_i)$

3.时序逻辑电路的分类

3.1 触发动作特点

根据触发器动作特点可分为同步时序逻辑电路和异步时序逻辑电路：
①在同步时序逻辑电路中，存储电路中所有触发器的时钟使用统一的CLK,状态变化发生在同一时刻，即触发器在时钟脉冲的作用下同时翻转;
②而在异步时序逻辑电路中，触发器的翻转不是同时的，没有统一的CLK，触发器状态的变化有先有后

3.2 输出信号特点

根据输出信号的特点时序逻辑电路可分为米利（Mealy）型和穆尔（Moore）型：
①在米利型时序逻辑电路中，输出信号不仅取决于存储电路的状态，而且还取决于输入变量,即Y=F(X,Q)
②在穆尔型时序逻辑电路中，输出信号仅仅取决于存储电路的状态，故穆尔型电路只是米利型电路的特例而已，可表述为Y=F(Q)

4.时序逻辑电路的分析方法

4.1 同步时序逻辑电路的分析方法

• 时序逻辑电路的分析：就是给定时序电路，找出该电路的逻辑功能，即找出在输入和CLK作用下，电路的次态和输出。由于同步时序逻辑电路是在同一时钟作用下，故分析比较简单些，只要写出电路的驱动方程、输出方程和状态方程，根据状态方程得到电路的状态表或状态转换图，就可以得出电路的逻辑功能。

4.1.1 步骤方法：

① 从给定的逻辑电路图中写出每个触发器的驱动方程（也就是存储电路中每个触发器输入信号的逻辑函数式）；
②把得到的驱动方程代入相应触发器的特性方程中，就可以得到每个触发器的状态方程，由这些状态方程得到整个时序逻辑电路的方程组；
③根据逻辑图写出电路的输出方程；
④写出整个电路的状态转换表、状态转换图和时序图；
⑤由状态转换表或状态转换图得出电路的逻辑功能

4.1.2 例子——穆尔型

分析图所示的时序逻辑电路的逻辑功能，写出它的驱动方程、状态方程和输出方程，写出电路的状态转换表，画出状态转换图和时序图

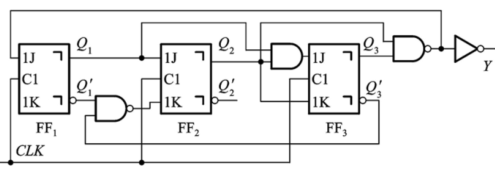
三个方程

解：

• 驱动方程：
  $J_1=(Q_2{Q}_3{)}^{\prime },K_1=1$
  $J_2=Q_1,K_2=(Q_1^{\prime }{Q}_3^{\prime }{)}^{\prime }$
  $J_3=Q_1{Q}_2,K_3=Q_2$
• 状态方程:
  JK触发器的特性方程：
  $Q^{\ast }=J{Q}^{\prime }+K^{\prime }Q$
  将驱动方程代入状态方程：
  $Q_1^{\ast }=(Q_2{Q}_3{)}^{\prime }{Q}_1^{\prime }$
  $Q_2^{\ast }=Q_1{Q}_2^{\prime }$
  $Q_3^{\ast }=Q_1{Q}_2{Q}_3^{\prime }+Q_2^{\prime }{Q}_3$
• 输出方程：
  $Y=Q_2{Q}_3$

逻辑电路的三个方程应该说已经清楚描述一个电路的逻辑功能，但却不能确定电路具体用途，因此需要在时钟信号作用下将电路所有的的状态转换全部列出，则电路的功能一目了然。

电路的各种状态图

• 描述时序逻辑电路所有状态的方法有状态转换表(状态转换真值表）、状态转换图、状态机流程图和时序图。下面结合上面的例题介绍这几种方法。

• 根据状态方程将所有的输入变量和电路初态的取值，代入电路的状态方程和输出方程，得到电路次态（新态)的输出值，列成表即为状态转换表，例子中的电路没有输入变量，属于穆尔型的时序逻辑电路，输出端只取决于电路的初态。
  假设电路的初始状态$Q_3{Q}_2{Q}_1=000$,
  则：由状态方程得到状态转换表：
  
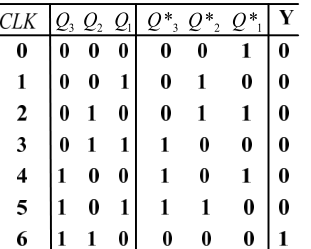
  而当电路的初始状态$Q_3{Q}_2{Q}_1=111$时，次态为000，输出为1
  所以由状态转换表得知，这是一个七进制加法计数器
  状态转换图如下所示
  
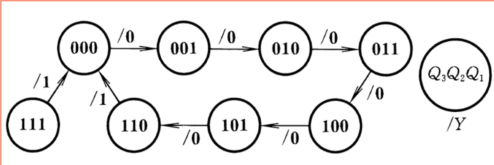
  进而可以得出时序图：
  

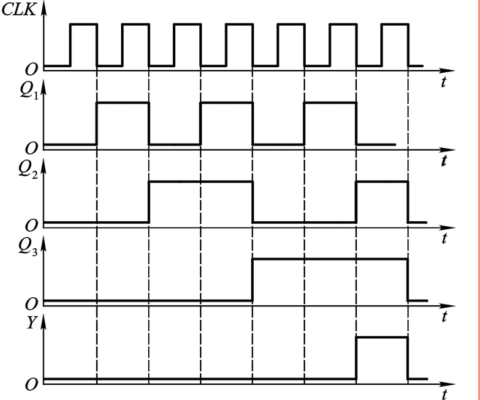
4.1.3 例子——米利型

分析图所示的时序逻辑电路的功能，写出电路的驱动
方程、状态方程和输出方程，画出电路的状态转换图

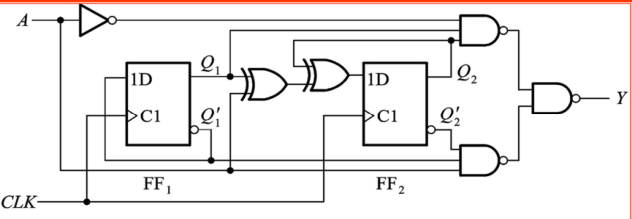
三个方程

驱动方程：
$D_1=Q_1^{\prime }$
$D_2=A\oplus Q_1\oplus Q_2$
状态方程：
$Q_1^{\ast }=D_1=Q_1^{\prime }$
$Q_2^{\ast }=D_2=A\oplus Q_1\oplus Q_2$
输出方程：
$Y=((A^{\prime }{Q}_1{Q}_2{)}^{\prime }(A{Q}_1^{\prime }{Q}_2^{\prime }{)}^{\prime }{)}^{\prime }=A^{\prime }{Q}_1{Q}_2+A{Q}_1^{\prime }{Q}_2^{\prime }$

各种状态图

最后

以上就是要减肥太阳为你收集整理的数电6_1——时序逻辑电路概述（很久整理的，没有下文）1.定义2. 时序逻辑电路的构成和结构特点3.时序逻辑电路的分类4.时序逻辑电路的分析方法的全部内容，希望文章能够帮你解决数电6_1——时序逻辑电路概述（很久整理的，没有下文）1.定义2. 时序逻辑电路的构成和结构特点3.时序逻辑电路的分类4.时序逻辑电路的分析方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。