概述
本篇笔记理解需要的内容：二进制的基本知识，如何用0，1表示二进制的正负，二进制的加减法等等。逻辑运算与或非；了解电路中的串联，并联，电阻等概念。
1.晶体管如何控制逻辑运算：
and:类似于电路中的串联，用两个晶体管串联在一起，可以实现“与”的功能。
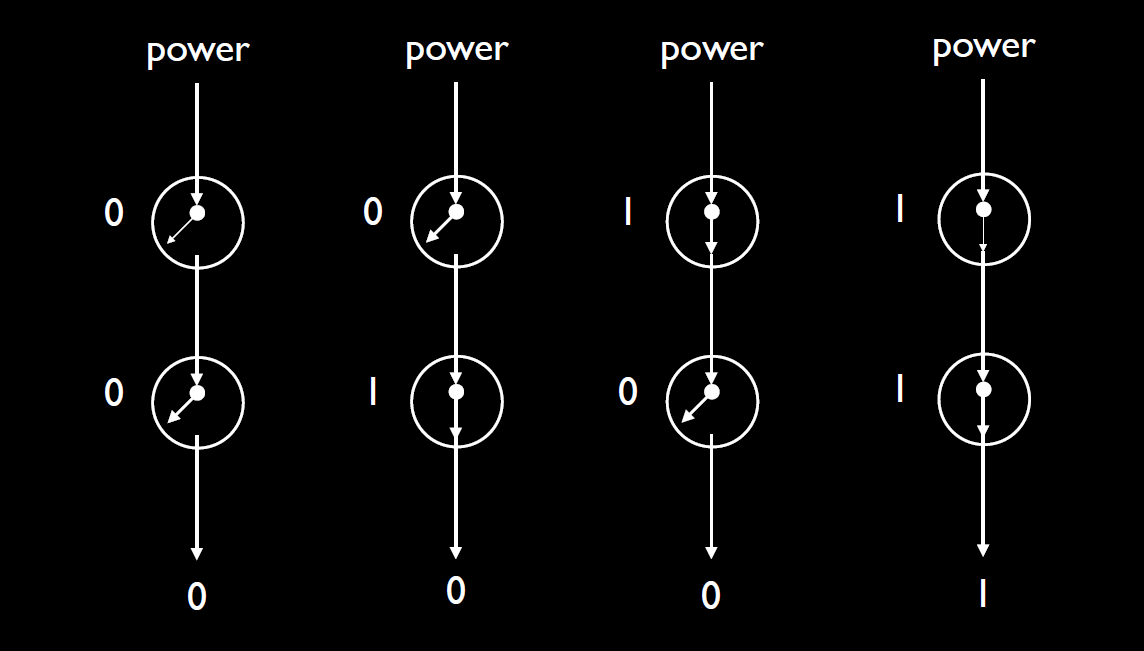
or：类似于电路中的并联，这样其中一个通路，就可以实现通路。即和‘或’的概念一致。
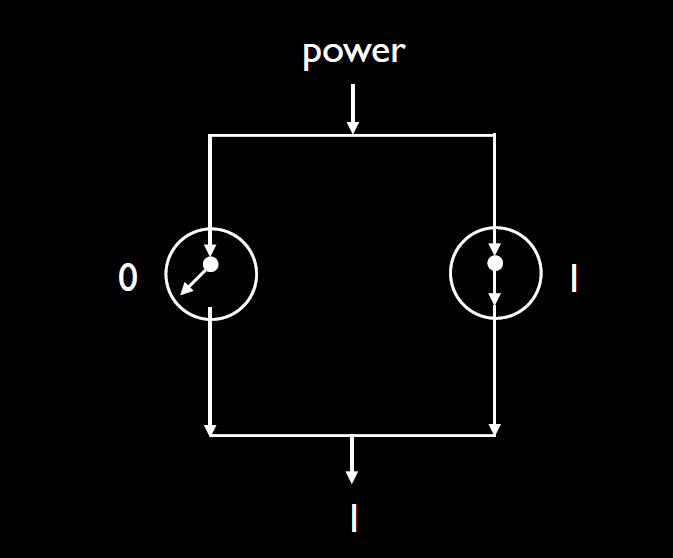
not: 类似短路和电阻的设计，图中的表就像开关，该支路是没有电阻的，都是输出是在有resistor的一端。如果开关闭合，即输入是1，则电阻端短路，不通过‘电流’，输出为0；如果输出为0，则开关断开，虽然有电阻，但是也会通过，输出为1。就实现了‘非’的功能。
总的来说，上面这些图的开关就是晶体管。实现一个‘与’‘或’的功能要两个晶体管。实现一个‘非’的功能要一个晶体管。
2.设计比较电路
上面我们知道了晶体管，那么实际过程中，计算机都是通过将代码转换为机器可以执行的二进制码，然后机器就允许这些二进制码就行了。那么我们电脑的电路也是只要设计可以执行二进制码的电路。我们来简单看一下几个简单的电路。
假设我们要实现一个比较两个1位数的二进制码（最简单的开始），那么我们先画个表格：
a,b束输入的，电路要实现的输出是c.只要把输出是1的内容，通过一个表达式表达出来。（注意这里只能用and和not来写表达式，后面你就知道为什么）。这里的表达式如下图所示。“'”表示非，"."表示和，“+”表示或。
因为有很多个输出为1的需要用or来联系在一起。所以我们先用and和not就不会乱。看表达式，根据表达式我们可以画出电路图了。
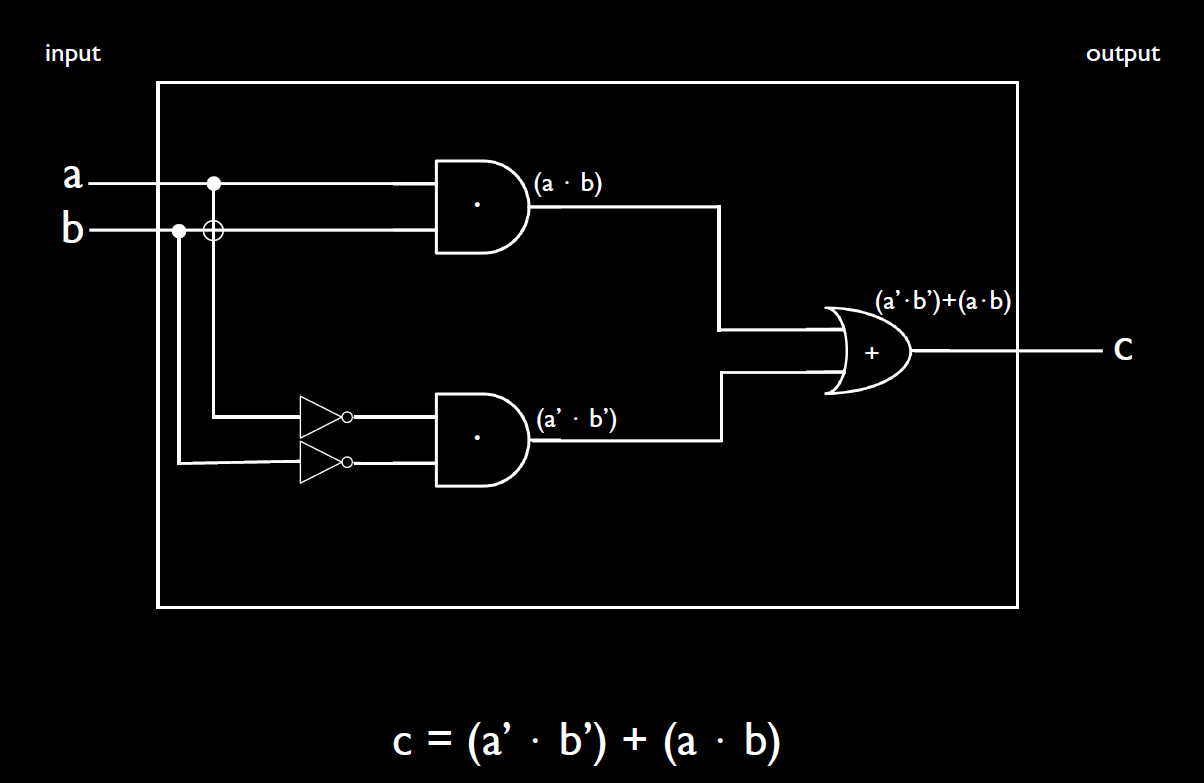
看这个电路图，是不是实现了确认两个1位二进制码的是否相同的功能。
这里总共用了 2*2(and)+1*2(or)+2*1(not)=8个晶体管
根据这个例子，我们可以总结出从功能设计到画电路图总共有以下步骤：
1.建立起对于输入所有的值，输出为1的表格
2.用and和not写出输出全部为1表达式（sub-expression）
3.用or将所有表达式串在一起（expression）
4.根据表达式画电路图。
我们再进阶，如果要比较两个4位二进制的数字是否相同？那么输入应该是8个数字，a1a2a3a4=b1b2b3b4?
首先我们将比较1位的当作一个小模块“1-CE(1-bit compare for equality)”
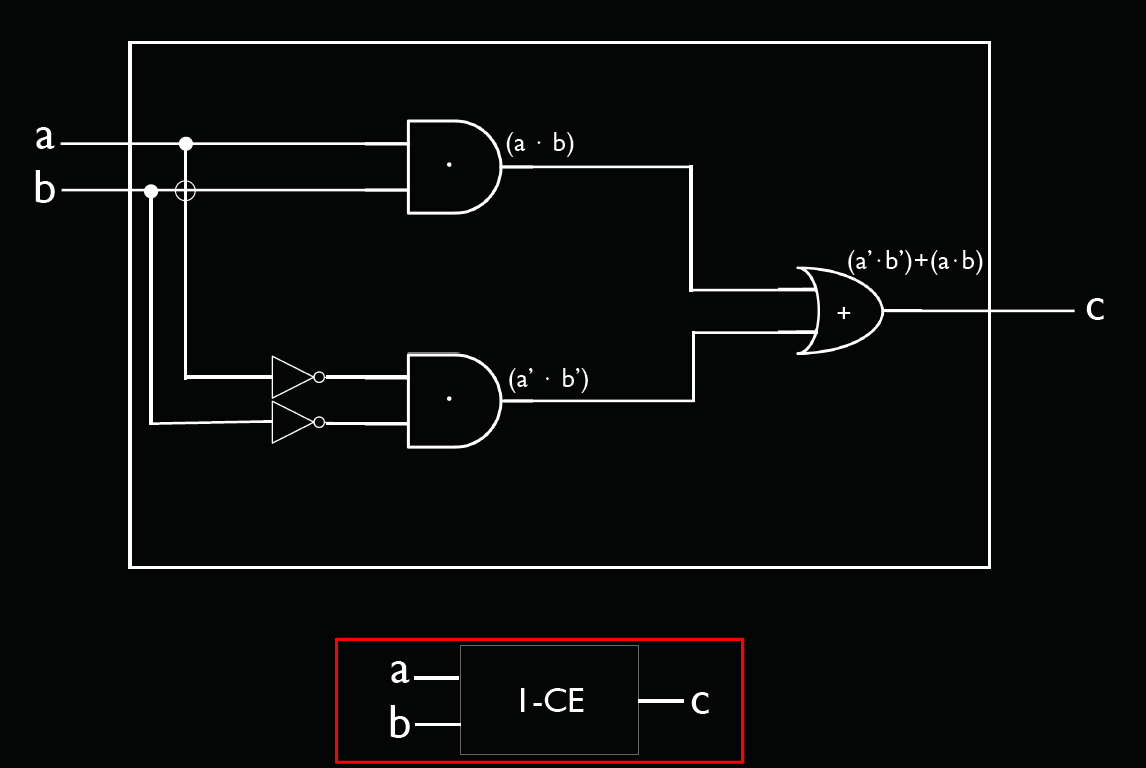
只要把小模块“1-CE”组合就可以变成"4-CE"(4-bits compare for equality),如下图所示。
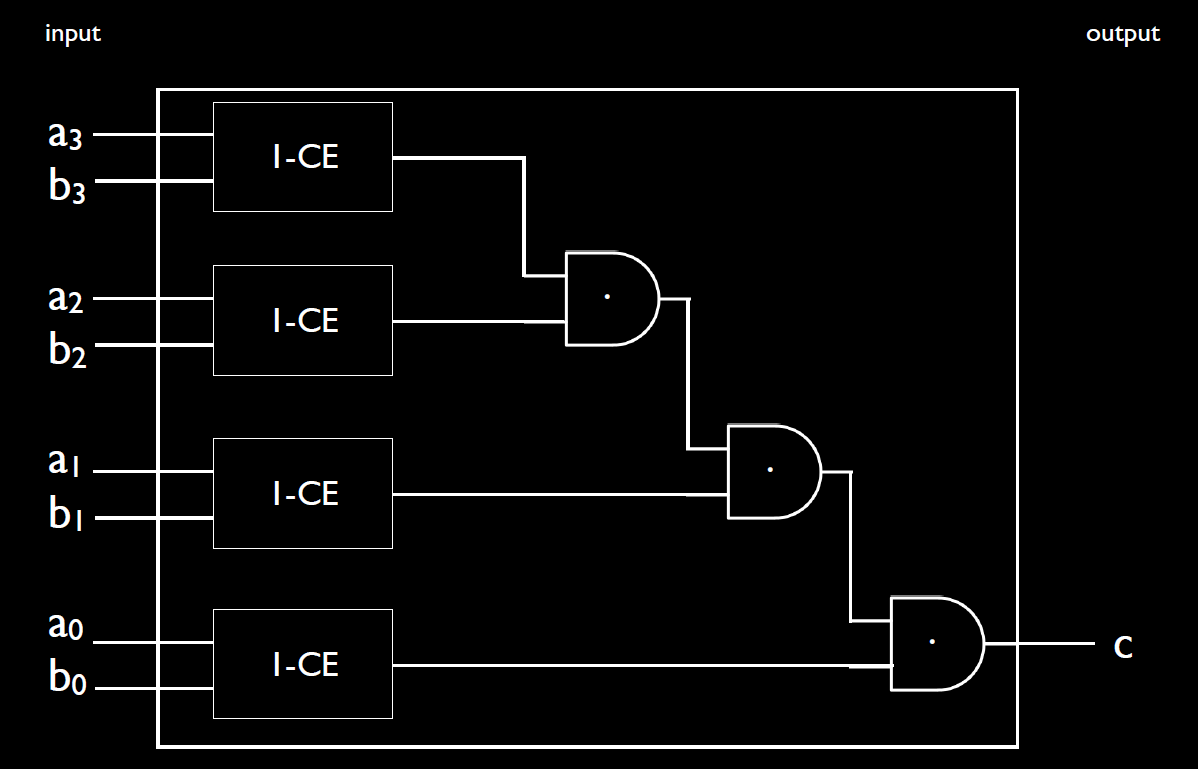
这里总共用了4*8（4个模块）+3*2=38个晶体管
好讲到这里，我们以及实现了代码里面的比较两个数值/字符/其他基本元素的大小（因为这些东西都可以化成二进制码）。那么如何实现加法这种功能？
3.加法电路
首先讨论一下二进制中的加减法，我们知道（不知道的话自己回去复习）二进制中的加减法需要额外的一位来表示进位。
我们先来实现以下1位数字的加法（1-bit Adder）
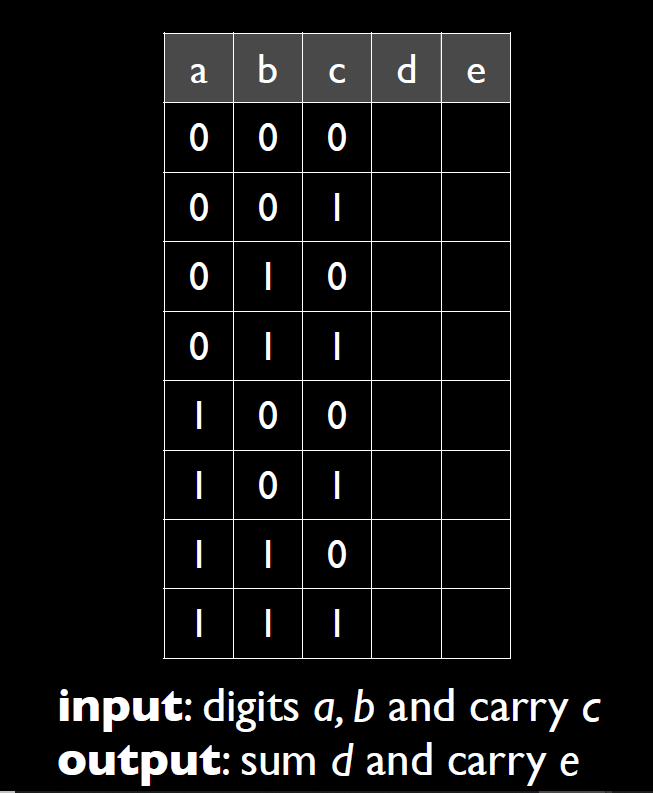
图中的carry就是进位。同样的我们先把sub-expression表达出来，但是这里要表达两次，因为有进位。
再用or的方法加起来。得到如下表达式：
d = (a'⋅b'⋅c) + (a'⋅b⋅c') + (a⋅b'⋅c') + (a⋅b⋅c)
e = (a'⋅b⋅c) + (a⋅b'⋅c) + (a⋅b⋅c') + (a⋅b⋅c)
根据表达式画出图，如下所示：
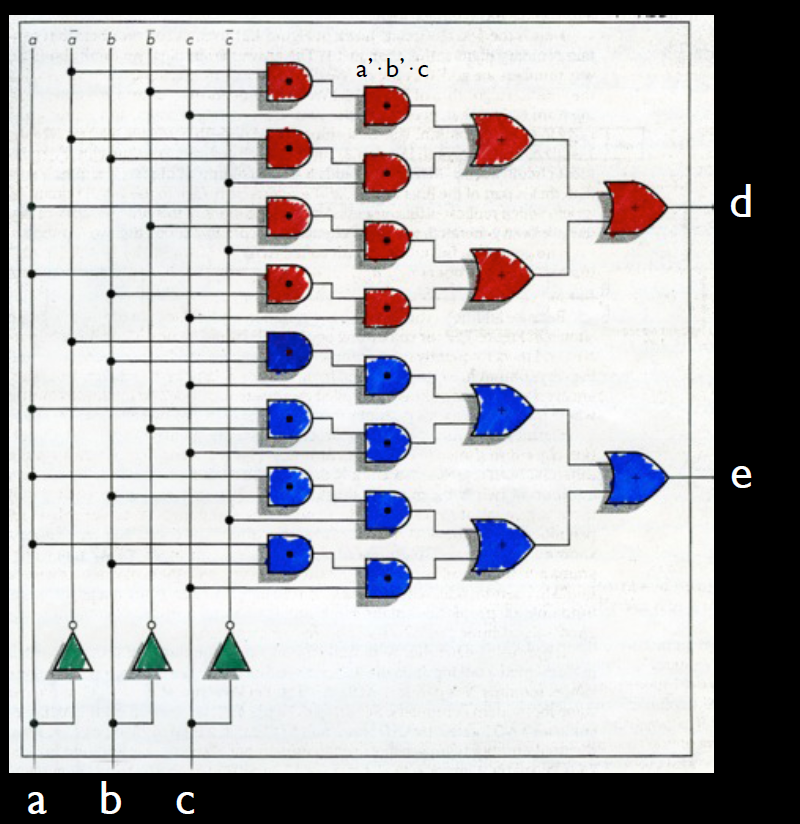
这里总共用了16*2(and)+6*2(or)+3*1(not)=47个晶体管
我们继续进一步，如果要画4位数的加法的电路图呢？和上面的方法一样，我们先将1-bit adder简化为一个模块
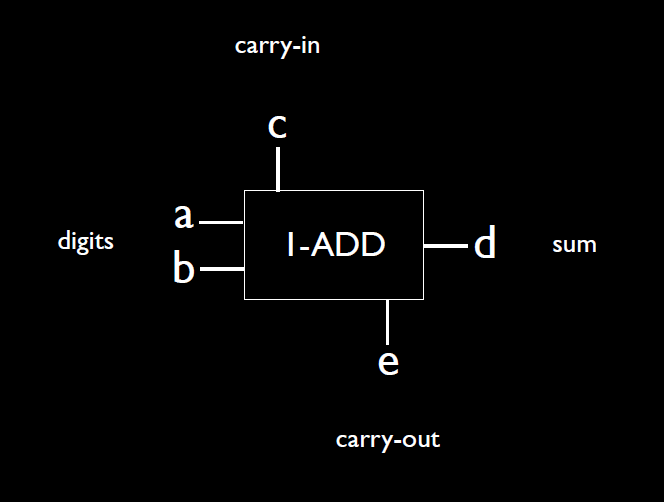
然后把模块组合就可以实现4-bits加法。其中上面的0是上一位的进位数，是设置为0的，最下面的进位如果有更多的位数是传给下个进位数的，这里没有了就悬空不管。
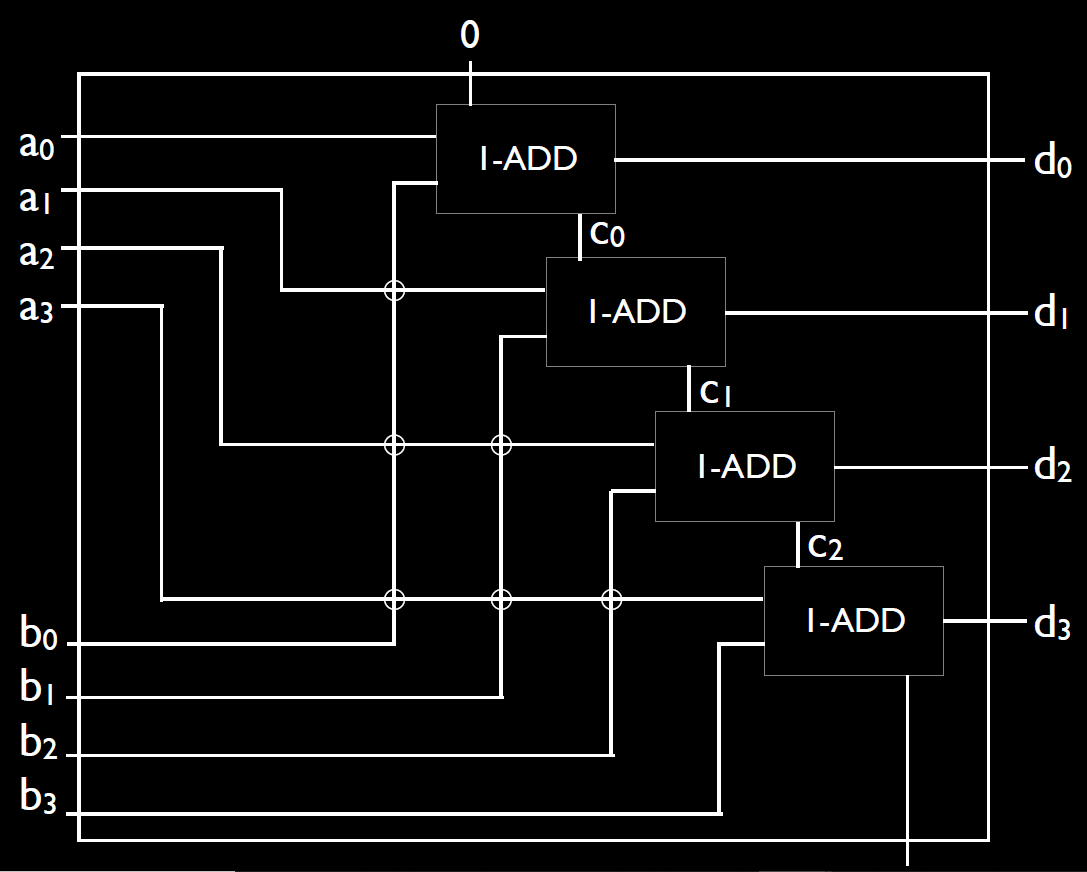
对于32bits adder则需要输入64个数字，总共需要的晶体管为47*32=1504个晶体管。
part3.简化电路图
一般来讲我们得到1bit adder的表格如下图所示：
换一种方法画他：
就是将两个数分开，表格上的束表示输出的值。这样画我们会发现有连续几个数都是1的位置。说明这个位置的数是和其中一个或两个对应输入是无关的，就可以简化表达式。（这个方法不熟悉可以去了解一下数电里面的内容）
表达式简化我们就可以根据简化表达式会出简化的电路。读者读到这里可以自己画一下这个电路，和前面的比较一下晶体管数是否更少了！
参考：
https://cs61a.org/
最后
以上就是魁梧鲜花为你收集整理的二进制和电路图的全部内容，希望文章能够帮你解决二进制和电路图所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复