fsolve
解非线性方程组
非线性系统解算器
解决指定的问题
F(x)= 0
对于x, F(x)是一个返回向量值的函数。
x是一个向量或者一个矩阵;看矩阵参数。
语法:
x = fsolve(fun,x0)
x = fsolve(fun,x0,options)
x = fsolve(problem)
[x,fval] = fsolve(___)
[x,fval,exitflag,output] = fsolve(___)
[x,fval,exitflag,output,jacobian] = fsolve(___)
描述:
1. x = fsolve(fun,x0) 从x0开始,试着解这些方程fun(x) = 0,一个0的数组。
实例:二维非线性系统的解
这个例子展示了如何在两个变量中求解两个非线性方程。方程是
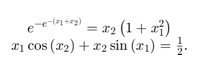
把方程转换成F(x)= 0形式。
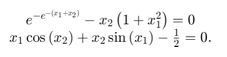
写一个函数,计算这两个方程的左边。
function F = root2d(x)
F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2);
F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
将此代码保存为一个名为root2d的文件在你的MATLAB搜索路径下。
求从点[0,0]开始的方程组。
fun = @root2d;
x0 = [0,0];
x = fsolve(fun,x0)
方程解决。
fsolve完成是因为函数值的向量在函数公差的默认值测量下接近于零,而这个问题在梯度测量下呈现出规律性。
x =
0.3532 0.6061
补充:MATLAB软件计算结果

方程解决。函数值的平方和r = 5.939402e-14小于sqrt(options.FunctionTolerance) = 1.000000e-03。r的梯度的相对范数r,2.023188e-07,小于选项OptimalityTolerance = 1.000000e-06。
| 优化指标 | 选项 |
|---|---|
| 相对范数(grad r) = 2.02e-07 | OptimalityTolerance = 1e-06 (default) |
| r = 5.94e-14 | sqrt(FunctionTolerance) = 1.0e-03 (default) |
2. x = fsolve(fun,x0,options)用选项中指定的优化选项解决方程。使用optimoptions来设置这些选项。
实例:具有非默认选项的解决方案
检查非线性系统的求解过程。
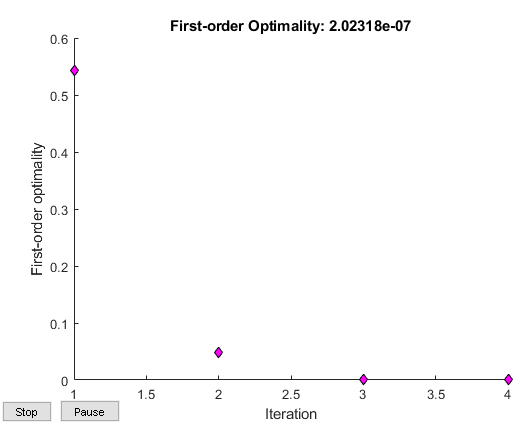
设置选项为无显示和一个显示一阶最优性的绘图函数,当算法迭代时,该函数应该收敛到0。
options = optimoptions('fsolve','Display','none','PlotFcn',@optimplotfirstorderopt);
非线性系统中的方程是
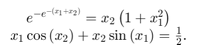
把方程转换成F(x)= 0形式。
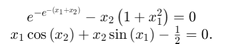
编写一个函数来计算这两个方程的左边。
function F = root2d(x)
F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2);
F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
将此代码保存为MATLAB®路径上名为root2d.m的文件。
从点[0,0]开始求解非线性方程组,观察求解过程。
fun = @root2d;
x0 = [0,0];
x = fsolve(fun,x0,options)
结果
x =
0.3532 0.6061
3. x = fsolve(problem)解决问题,其中问题是在Input Arguments中描述的结构。通过从优化应用程序导出问题来创建问题结构,如Exporting Your Work中所述。
实例:解决一个问题结构体
为fsolve创建问题结构体并解决问题。
使用非默认选项解决与解决方案相同的问题,但是使用问题结构体表示问题。
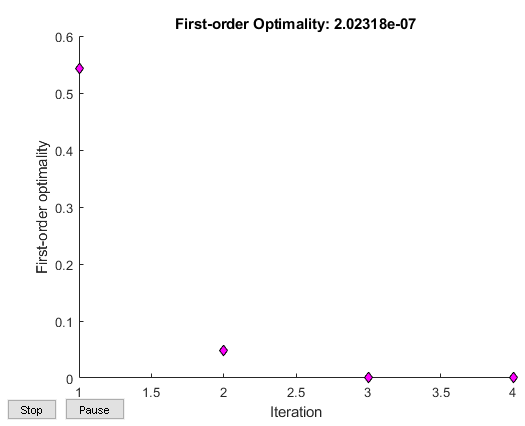
设置没有显示的问题选项和显示一阶最优性的绘图函数,当算法迭代时,它应该收敛到0。
problem.options = optimoptions('fsolve','Display','none','PlotFcn',@optimplotfirstorderopt);
非线性系统中的方程是
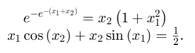
把方程转换成F(x)= 0形式。
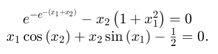
编写一个函数来计算这两个方程的左边。
function F = root2d(x)
F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2);
F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;
将此代码保存为MATLAB®路径上名为root2d.m的文件。
在问题结构中创建其余字段。
problem.objective = @root2d;
problem.x0 = [0,0];
problem.solver = 'fsolve';
解决这个问题。
x = fsolve(problem)
x =
0.3532 0.6061
4. [x,fval] = fsolve(___),对于任何语法,返回在解决方案x处目标函数fun的值。
实例:非线性系统的解过程
此示例返回迭代显示,显示两个方程和两个未知数的系统的求解过程
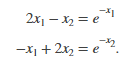
以F(x)= 0的形式重写方程式:
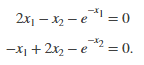
在x0 =[-5 -5]中开始寻找解决方案。
首先,写一个计算F的文件,计算方程在x处的值。
function F = myfun(x)
F = [2*x(1) - x(2) - exp(-x(1));
-x(1) + 2*x(2) - exp(-x(2))];
在MATLAB®路径上将此函数文件另存为myfun.m. 设置初始点。设置options以返回迭代显示。
x0 = [-5;-5];
options = optimoptions('fsolve','Display','iter');
调用fsolve。
[x,fval] = fsolve(@myfun,x0,options)
| Iteration 迭代 | Func- count | f(x) | Norm of step | First-order optimality 一阶最优性 | Trust-region radius 信赖域半径 |
|---|---|---|---|---|---|
| 0 | 3 | 23535.6 | 2.29e+004 | 1 | |
| 1 | 6 | 6001.72 | 1 | 5.75e+003 | 1 |
| 2 | 9 | 1573.51 | 1 | 1.47e+003 | 1 |
| 3 | 12 | 427.226 | 1 | 388 | 1 |
| 4 | 15 | 119.763 | 1 | 107 | 1 |
| 5 | 18 | 33.5206 | 1 | 30.8 | 1 |
| 6 | 21 | 8.35208 | 1 | 9.05 | 1 |
| 7 | 24 | 1.21394 | 1 | 2.26 | 1 |
| 8 | 27 | 0.016329 | 0.759511 | 0.206 | 2.5 |
| 9 | 30 | 3.51575e-006 | 0.111927 | 0.00294 | 2.5 |
| 10 | 33 | 1.64763e-013 | 0.00169132 | 6.36e-007 | 2.5 |
方程解决。
fsolve完成是因为函数值的向量在函数公差的默认值测量下接近于零,而这个问题在梯度测量下呈现出规律性。
x =
0.5671
0.5671
fval =
1.0e-006 *
-0.4059
-0.4059
补充:
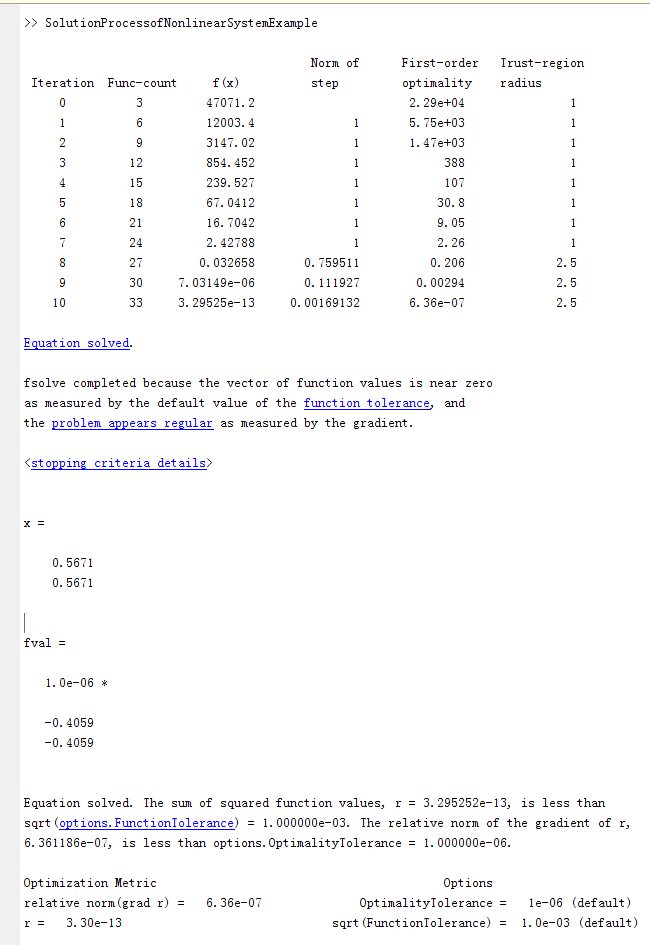
方程解决。函数值的平方和r = 3.295252e-13,小于
√options.FunctionTolerance = 1.000000 e 03。r的梯度的相对范数,6.361186 -07,小于options。OptimalityTolerance = 1.000000 e-06。
优化指标的选择
相对范数(grad r) = 6.36e-07 OptimalityTolerance= 1e-06(默认)
r = 3.30 e-13 √FunctionTolerance = 1.0 e-03(默认)
5. [x,fval,exitflag,output] = fsolve(___)另外返回一个描述fsolve退出条件的exitflag值,以及一个包含优化过程信息的结构output。
实例:检验矩阵方程解
找到一个满足的矩阵X
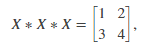
从点x=[1,1;1,1]开始。检查fsolve输出,查看解决方案的质量和过程。
创建一个匿名函数来计算矩阵方程。
fun = @(x)x*x*x - [1,2;3,4];
设置关闭显示的选项。设初始点x0。
options = optimoptions('fsolve','Display','off');
x0 = ones(2);
调用fsolve并获取有关解决过程的信息。
x =
-0.1291 0.8602
1.2903 1.1612
fval =
1.0e-09 *
-0.1618 0.0778
0.1160 -0.0474
exitflag =
1
退出标志值1表示解决方案是可靠的。为了手工验证这一点,计算残差(fval的平方和),看看它离零有多近。
sum(sum(fval.*fval))
ans =
4.7957e-20
这个小残差证实了x是一个解。
正如您在输出结构中看到的,fsolve执行了35个函数计算来找到解决方案。
output.funcCount
ans =
35
- [x,fval,exitflag,output,jacobian] = fsolve(___)返回在解x处的fun函数的雅可比矩阵。
输入参数
fun — 非线性方程求解
函数句柄 | 函数名
要求解的非线性方程,指定为函数句柄或函数名。 fun是一个接受向量x并返回向量F的函数,向量F是在x处取值的非线性方程。对于F的所有分量,要求解的等式是F = 0.函数fun可以被指定为文件的函数句柄
x = fsolve(@myfun,x0)
其中 myfun 是一个MATLAB函数,比如
function F = myfun(x)
F = ... % 计算函数在x点的值
fun 也可以是匿名函数的函数句柄。
x = fsolve(@(x)sin(x.*x),x0);
如果x和F的用户定义值是矩阵,则使用线性索引(MATLAB)将它们转换为向量。
如果雅可比矩阵也可以计算并且雅可比矩阵选项是“on”,则由
options = optimoptions('fsolve','SpecifyObjectiveGradient','on')
函数fun必须在第二个输出参数中返回雅可比值J,即x处的矩阵。
如果fun返回m个分量的向量(矩阵)并且x具有长度n,其中n是x0的长度,则雅可比J是m*n矩阵,其中J(i,j)是F( i)关于x(j)的偏导数。 (雅可比J是F渐变的转置)
Example: fun = @(x)xxx-[1,2;3,4]
Data Types: char | function_handle | string
x0 — 起始点
实向量| 实数组
初始点,指定为实向量或实数组。fsolve使用元素的数量和x0的大小来确定fun接受的变量的数量和大小。
Example: x0 = [1,2,3,4]
Data Types: double
options — 优化选项
输出的优化选项 | 结构作为优化集返回
优化选项,指定为优化选项的输出或优化集返回等结构。
一些选项适用于所有算法,另一些选项与特定算法相关。有关详细信息,请参见优化选项参考。从Optimization Options Reference 查看详细信息.
优化选项显示中缺少一些选项。这些选项以斜体列出。有关详细信息,请参见View Options。
| 所有的算法 | |
|---|---|
| 算法 Algorithm | 在“trust-region-dogleg”(默认)、“trust-region”和“levenberg-marquardt”之间进行选择。 Algorithm选项指定要使用哪种算法作为首选项。这只是一个偏好,因为对于trust-region算法,非线性方程组不能是欠定义的;也就是说,方程的数量(由fun返回的F的元素数量)必须至少与x的长度一样多。同样,对于trust-region-dogleg算法,方程的数量必须与x的长度相同。当所选算法不可用时,fsolve使用Levenberg-Marquardt算法。有关选择算法的更多信息,请参阅Choosing the Algorithm。 要使用optimset而不是optimoptions设置一些算法选项: Algorithm - 将算法设置为’trust-region-reflective’而不是’trust-region’。 InitDamping - 通过将Algorithm 设置为单元数组(例如{‘levenberg-marquardt’,.005})来设置初始Levenberg-Marquardt参数λ。 |
| CheckGradients 检查梯度 | 比较用户提供的导数(目标或约束的梯度)和有限差分导数。选项为真或默认为假。 对于optimset,名称是derivative ativecheck,值是“on”或“off”。参见Current and Legacy Option Name Tables.当前和遗留选项名称表。 |
| Diagnostics 诊断 | 显示要达到最低限度的或求解的函数的诊断信息。选项是“on”或默认为“off”。 |
| DiffMaxChange 差异极大值变化 | 有限差分梯度(一个正标量)变量的最大变化量。默认是Inf。 |
| DiffMinChange 差异极小值变化 | 有限差分梯度(一个正标量)变量的最小变化量。默认值是0。 |
| Display 显示 | 显示级别(参见迭代显示): 'off’或’none’不显示输出。 'iter’在每次迭代时显示输出,并给出默认的退出消息。 'iter-detailed’在每次迭代时显示输出,并给出技术退出消息。 ‘final’(默认值)仅显示最终输出,并提供默认退出消息。 'final-detailed’显示最终输出,并给出技术退出消息。 |
| FiniteDifferenceStepSize 有限差分步长 | 有限差分的标量或向量步长因子。当你将有限差分步长设置为向量v时,正向有限差分步长为: delta = v.*sign′(x).*max(abs(x),TypicalX); sign′(x) = sign(x) except sign′(0) = 1。中心有限差分为: delta = v.*max(abs(x),TypicalX); 标量FiniteDifferenceStepSize 扩展为一个向量。默认是sqrt(eps)向前有限的差异,和eps ^(1/3)中央有限的差异。 对于optimset,名称是FinDiffRelStep。参见Current and Legacy Option Name Tables.当前和遗留选项名称表。 |
| FiniteDifferenceType 有限差分类型 | 有限差分,用来估计梯度,要么是“forward”(默认),要么是“central”(居中)。“central”需要两倍的函数求值,但应该更准确。 该算法在估计两种类型的有限差分时,都注意遵守边界。例如,为了避免在边界外求值,它可以取一个反向的差,而不是正向的差。 对于optimset,名称是FinDiffType。参见Current and Legacy Option Name Tables当前和遗留选项名称表。 |
| FunctionTolerance 函数公差 | 函数值上的终止公差,为正标量。默认值是1e-6。见 Tolerances and Stopping Criteria.公差和停止标准。 对于optimset,名称是TolFun。参见 Current and Legacy Option Name Tables.当前和遗留选项名称表。 |
| FunValCheck 函数值检查 | 检查目标函数值是否有效。'on’在目标函数返回complex、Inf或NaN值时显示错误。默认的“off”不会显示错误。 |
| MaxFunctionEvaluations Max函数评价 | 允许的函数计算的最大数目,一个正整数。默认值是100*numberOfVariables。参见Tolerances and Stopping Criteria公差和停止标准、Iterations and Function Counts.迭代和函数计数。 对于optimset,名称是MaxFunEvals。参见当前和遗留选项名称表。 |
| MaxIterations 最大迭代次数 | 允许的最大迭代次数,一个正整数。默认值是400。参见Tolerances and Stopping Criteria公差和停止标准 、Iterations and Function Counts迭代和功能计数。 对于optimset,它的名称是MaxIter。参见Current and Legacy Option Name Tables当前和遗留选项名称表。 |
| OptimalityTolerance 最优公差 | 一阶最优解的终止公差,一个正标量。默认值是1e-6。见First-Order Optimality Measure一阶最优测度。 在内部,“levenberg-marquardt”算法使用最优公差(停止准则)为FunctionTolerance的1e-4倍,而不使用OptimalityTolerance。 |
| OutputFcn 输出函数 | 指定优化函数在每次迭代时调用的一个或多个用户定义函数。传递函数句柄或函数句柄的单元数组。默认值是none([])。查看 Output Function.函数输出。 |
| PlotFcn 绘图函数 | 绘制算法执行过程中的各种进度度量;从预定义的图中选择或编写您自己的图。传递一个内置的绘图函数名、函数句柄或包含内置绘图函数名或函数句柄的单元格数组。对于自定义绘图函数,传递函数句柄。默认为none ([]): “optimplotx”绘制当前点。 'optimplotfunccount’绘制函数计数图。 'optimplotfval’绘制函数值。 'optimplotstepsize’绘制步骤大小。 'optimplotfirstorderopt’绘制一阶最优度量。 有关编写自定义绘图函数的信息,请参见Plot Functions.绘图函数。 对于optimset,名称是PlotFcns。参见 Current and Legacy Option Name Tables.当前和遗留选项名称表。 |
| SpecifyObjectiveGradient 指定目标梯度 | 如果为真,fsolve使用用户定义的雅可比矩阵(在fun中定义的)或雅可比矩阵信息(在使用雅可比矩阵multiplyfcn时)作为目标函数。如果为假(默认),fsolve使用有限差分近似雅可比矩阵。 对于optimset,其名称为雅可比矩阵,值为“on”或“off”。参见Current and Legacy Option Name Tables.当前和遗留选项名称表。 |
| StepTolerance | 对x的终止公差,一个正标量。默认值是1e-6。见公差和停止标准。 对于optimset,名称是TolX。参见Current and Legacy Option Name Tables.当前和遗留选项名称表。 |
| TypicalX | 典型的x值。TypicalX中的元素数量通常等于起点x0中的元素数量。默认值是1 (数量的变量,1)。fsolve使用TypicalX缩放有限差分进行梯度估计。 trust-region-dogleg算法通常使用TypicalX作为缩放矩阵的对角线项。 |
| UseParallel | 为真时,fsolve并行估计梯度。通过设置为默认值false禁用。参见Parallel Computing.并行计算。 |
| Levenberg-Marquardt Algorithm | |
|---|---|
| InitDamping | Levenberg-Marquardt参数的初值,一个正标量。默认是1e-2。详见Levenberg-Marquardt方法。 |
| ScaleProblem 规模问题 | 'jacobian’有时可以改进尺度较差问题的收敛性。默认值是“none”。 |
Example: options = optimoptions(‘fsolve’,‘FiniteDifferenceType’,‘central’)
补充:
Choosing the Algorithm
fsolve Algorithms
fsolve 有三种算法:
‘trust-region-dogleg’ (默认)
‘trust-region’
‘levenberg-marquardt’
使用optimoptions在命令行设置算法选项。
建议
首先使用“trust-region-dogleg”算法。
如果fsolve失败,请查看该解决程序When the Solver Fail或When the Solver Might Have Succeeded。
如果您有一个雅可比矩阵乘法函数,或者希望优化内部算法(请参阅fsolve options中的Trust-Region Algorithm),请尝试“Trust-Region”再次求解方程。
尝试计时所有的算法,包括“levenberg-marquardt”,以找到最适合您的问题的算法。
建议背后的原因
“trust-region-dogleg”是唯一一种专门用于求解非线性方程的算法。其他的则试图最小化函数的平方和。
'trust-region’算法对稀疏问题是有效的。它可以使用特殊的技术,如雅可比矩阵乘函数的大规模问题。
有关算法的描述,请参见Equation Solving Algorithms。
problem — Problem structure
structure
问题结构,指定为具有以下字段的结构:
| Field Name | Entry |
|---|---|
| objective | 目标函数 |
| x0 | x的起始点 |
| solver | ‘fsolve’ |
| options | 使用optimoptions创建的选项 |
获得问题结构的最简单方法是从Optimization app优化应用程序导出问题。
Data Types: struct
输出参数
x -解
实向量|实数数组
解,作为实向量或实数组返回。x的大小等于x0的大小。通常,当exitflag为正数时,x是问题的本地解决方案。有关解决方案质量的信息,请参见When the Solver Succeeds.解决程序何时成功。
fval -目标函数在解处的值
真正的向量
目标函数在解处的值,作为实向量返回。一般来说,fval = fun(x)。
exitflag -原因fsolve停止
整数
原因fsolve停止,返回一个整数。
| 1 | 方程解决。一阶最优性很小。 |
|---|---|
| 2 | 方程解决。改变x小于指定的公差。 |
| 3 | 方程解决。残余变化小于规定公差。 |
| 4 | 方程解决。搜索方向的大小小于指定的公差。 |
| 0 | 超出迭代次数options.MaxIterations或者超出函数计算的次数options.MaxFunctionEvaluations. |
| -1 | 输出函数或绘图函数停止算法。 |
| -2 | 方程没有解决。退出消息可以包含更多信息。 |
| -3 | 方程没有解决。信任区域半径太小(trust-region-dogleg算法)。 |
output-关于优化过程的信息
结构
关于优化过程的信息,以字段结构形式返回:
| iterations | 迭代次数 |
|---|---|
| funcCount | 函数估算次数 |
| algorithm | 优化算法 |
| cgiterations | PCG迭代总次数(仅’trust-region’算法) |
| stepsize | x的最终位移(不在“trust-region-dogleg”中) |
| firstorderopt | 一阶最优性的度量 |
| message | 退出消息 |
jacobian-解的雅可比矩阵
真正的矩阵
解的雅可比矩阵,作为实矩阵返回。jacobian(i,j) 是fun(i) 关于x(j)在解x处的偏导数。
局限性
要解的函数必须是连续的。
成功时,fsolve只给出一个根。
默认的trust-region dogleg方法只能在方程组为正方形时使用,即,方程的数量等于未知数的数量。对于Levenberg-Marquardt方法,方程组不需要是平方的。
trust-region算法的共轭梯度预处理部分的预处理计算在计算预处理前形成JTJ(其中J为雅可比矩阵);因此,一排带有许多非零的J,会导致JTJ产品的密度接近于零,这可能会导致解决大型问题的过程成本高昂。
算法
Levenberg-Marquardt和trust-region方法是基于非线性最小二乘算法也用于lsqnonlin中。如果系统可能没有零,请使用其中一种方法。该算法仍然返回一个残差较小的点。但是,如果系统的雅可比矩阵是奇异的,那么算法可能收敛到一个不是方程组解的点(参见局限性)。
fsolve在默认情况下选择trust-region dogleg算法。该算法是[8]中描述的Powell dogleg方法的变体。它本质上类似于[7]中实现的算法。见 Trust-Region Dogleg Method。
trust-region算法是一种子空间信赖域方法,基于[1]和[2]中描述的内反射牛顿法。每一次迭代都涉及到使用预先条件共轭梯度法(PCG)求解大型线性系统的近似解。参见 Trust-Region fsolve Algorithm。
Levenberg-Marquardt方法在文献[4]、[5]和[6]中有描述。查看Levenberg-Marquardt Method。
最后
以上就是甜美睫毛最近收集整理的关于MATLAB-fsolve函数帮助文档翻译与补充fsolve的全部内容,更多相关MATLAB-fsolve函数帮助文档翻译与补充fsolve内容请搜索靠谱客的其他文章。







![matlab 计算终止,[MATLAB工具箱] 利用函数fmincon求解非线性方程时遇到计算提前终止的问题...](https://www.shuijiaxian.com/files_image/reation/bcimg7.png)
发表评论 取消回复