一文教你快速搞懂速度曲线规划之S形曲线（超详细+图文+推导+附件代码）

加入技术交流群

领取资料

本文介绍了运动控制终的S曲线，通过matlab和C语言实现并进行仿真；本文篇幅较长，请自备茶水；
请帮忙点个赞 ????????????；
请帮忙点个赞 ????????????；
请帮忙点个赞 ????????????；

之前有介绍过T形曲线，具体可以参考《一文教你快速搞懂速度曲线规划之T形曲线》，本文将在原先的基础上进行进一步扩展，另外由于介绍速度曲线的论文较多，本文会在具体引用的地方给出原文出处；先对比一下两者的差别；

网图侵删

1 前言

S形加减速的最重要特征是该算法的加速度/减速度曲线的形状如字母 S。S形加减速的速度曲线平滑 ,从而能够减少对控制过程中的冲击，并使插补过程具有柔性 ¹。
由于T形曲线在加速到匀速的切换过程中，实际中存在较大过冲，因此这里对比一下T曲线和7段S曲线的实际过程；

• T形：加速 -> 匀速 -> 减速
• S形：加加速($T_1$) -> 匀加速($T_2$) -> 减加速($T_3$)-> 匀速($T_4$)-> 加减速($T_5$)-> 匀减速($T_6$)-> 减减速($T_7$)

上文在加速这块的文字描述可能读起来起来有点绕，下面看图：

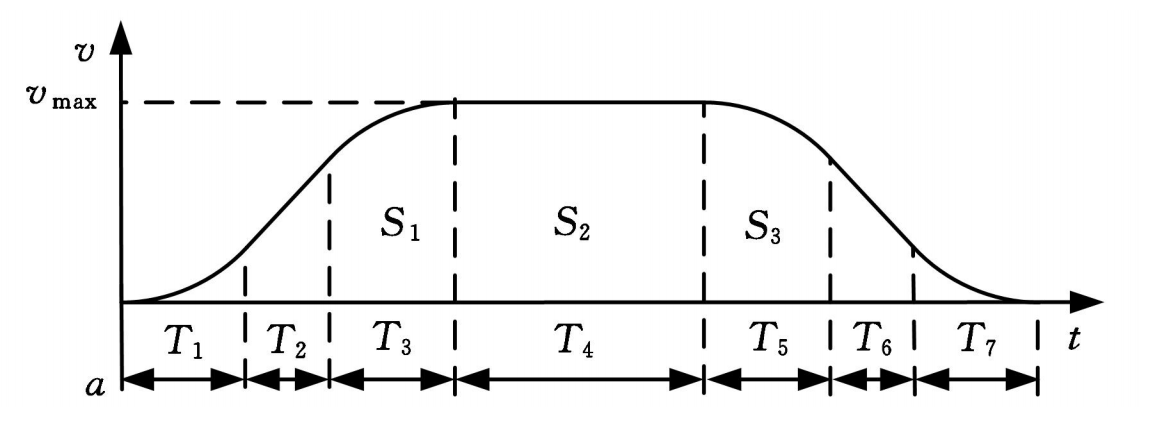
2 理论分析

由于S曲线在加减速的过程中，其加速度是变化的，因此这里引入了新的一个变量 $J$，即加加速度。
$$J=\frac{d_a}{d_t}$$
因此对应上图的7段S速度曲线中，规定最大加速为$a_{max}$，最小加速度为$-a_{max}$，则加速度的关系；

• 加加速($T_1$)：$a$逐渐增大，此时$a=J{T}_1,0<t\le t_1;$
• 匀加速($T_2$)：$a$达到最大，此时$a=a_{max},t_1<t\le t_2;$
• 减加速($T_3$)：$a$逐渐减小，此时$a=a_{max}-J{T}_3,t_2<t\le t_3;$
• 匀速($T_4$)：$a$不变化，此时$a=0,t_3<t\le t_4;$
• 加减速($T_5$)：$|a|$ 逐渐增大，此时$a=-J{T}_5,t_4<t\le t_5;$
• 匀减速($T_6$)：$|a|$ 达到最大，此时$a=-a_{max},t_5<t\le t_6;$
• 减减速($T_7$)：$|a|$ 逐渐减小，此时$a=-a_{max}+-J{T}_7,t_6<t\le t_7;$

$|a|$ 为加速度的绝对值；
其中 $T_k=t_k-t_{k-1}(k=1,...,7)$

所以通常需要确定三个最基本的系统参数 :系统最大速度 $v_{max}$ ，最大加速度a_{max} ，加加速度$J$，就可以可确定整个运行过程² ；

• 最大速度：反映了系统的最大运行能力 ；
• 最大加速度：反映了系统的最大加减速能力 ；
• 加加速度：反映了系统的柔性；
  • 柔性越大，过冲越大，运行时间越短；
  • 柔性越小，过冲越小，运行时间越长；

2.1 加速度时间关系方程

整个加速度变化的过程具体如下图所示；


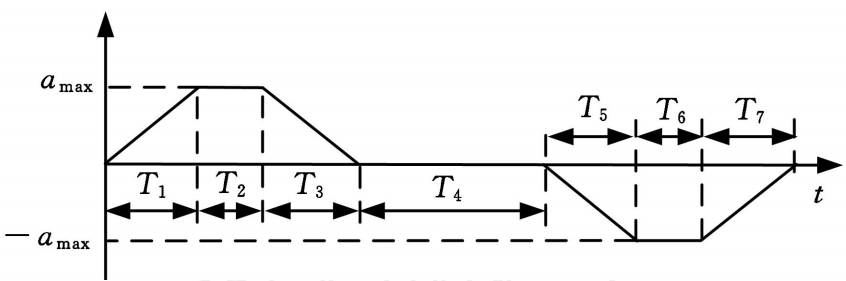
再次强调一下 $T$ 和 $t$ 的关系，$T_k=t_k-t_{k-1}(k=1,...,7)$
另外这里再引入变量 $\tau$，
$${\tau }_k=t-t_{k-1}\cdots ①$$
比如，当前时刻 $t_2<t\le t_3$ ,即 $t$ 位于区间 $T_3$，则如果将 $t_2$ 作为初始点，则 ${\tau }_3$为 $t$ 相对于$t_2$时刻的时间，则有：
$${\tau }_3=t-t_2$$
下面可以得到加速度与时间的关系函数，具体如下：
$$\begin{array}{r}a(t)=\{\begin{array}{ll}Jt,& 0<t\le t_1\\ a_{max},& t_1<t\le t_2\\ a_{max}-J(t-t_2),& t_2<t\le t_3\\ 0,& t_3<t\le t_4\\ -J(t-t_4),& t_4<t\le t_5\\ -a_{max},& t_5<t\le t_6\\ -a_{max}-J(t-t_6),& t_6<t\le t_7\end{array}\end{array}\cdots ②$$

根据 ① 式，将 $\tau$ 代入 ② 式可以得到：
$$\begin{array}{r}a(t)=\{\begin{array}{ll}J{\tau }_1,& 0<t\le t_1\\ a_{max},& t_1<t\le t_2\\ a_{max}-J{\tau }_3,& t_2<t\le t_3\\ 0,& t_3<t\le t_4\\ -J{\tau }_3,& t_4<t\le t_5\\ -a_{max},& t_5<t\le t_6\\ -a_{max}+J{\tau }_7,& t_6<t\le t_7\end{array}\end{array}$$

上式中 $J>0$；

2.2 速度时间关系方程

速度和加速度满足 $v=at$ ；加加速度和速度的关系满足：
$$v=\frac{1}{2}J{t}^2$$

结合加速度时间关系并结合② 式可以得到速度曲线关系，具体关系如下图所示；





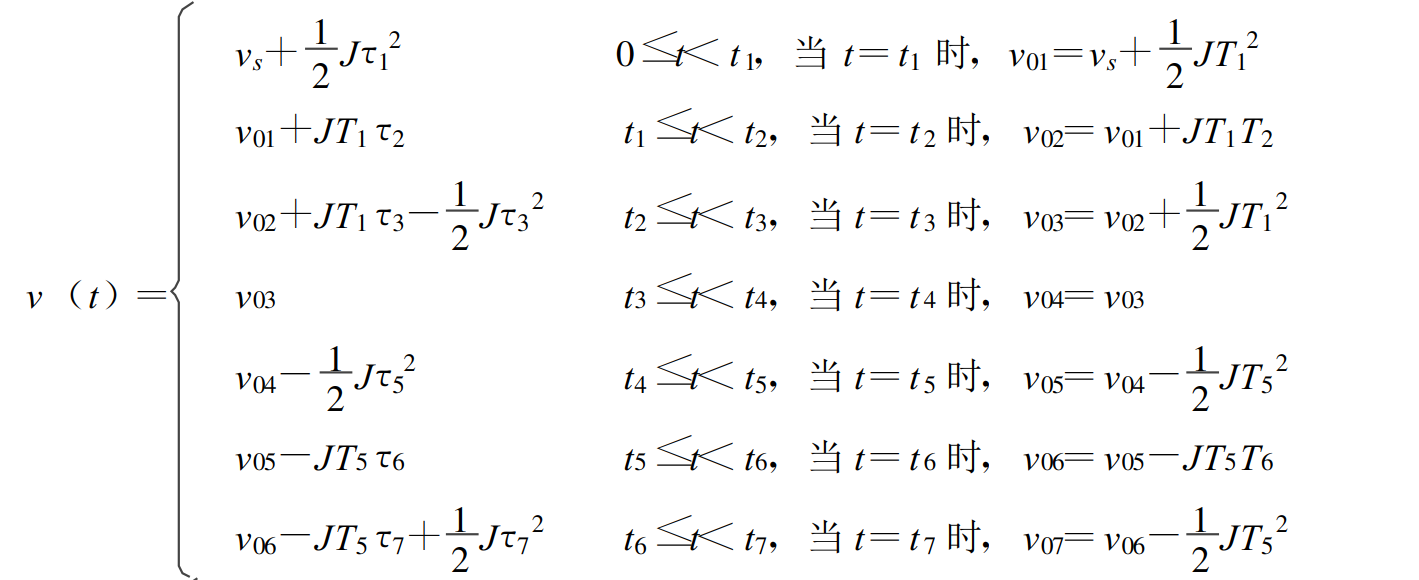
进一步简化可以得到：

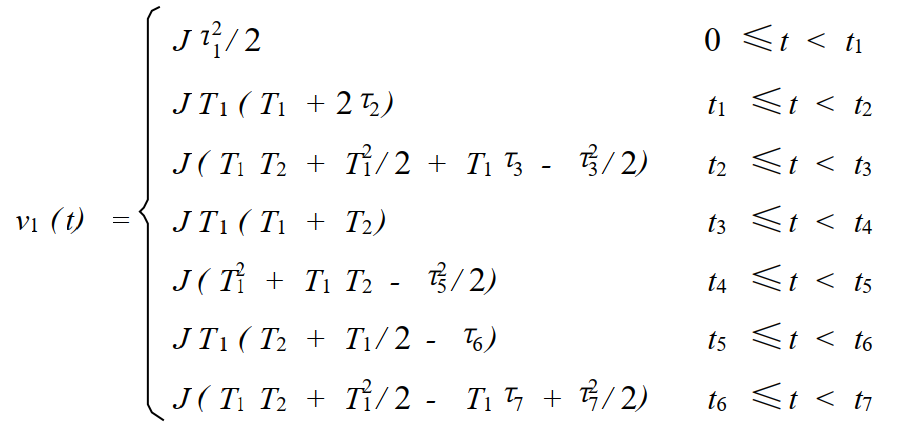
2.3 位移时间关系方程

位移 $S$ 和加加速度 $J$ 直接满足关系如下：
$$S=\frac{1}{6}J{t}^3$$

简单推导
$$\{\begin{array}{l}S={\int }_0^{t}vdt\\ v=\frac{1}{2}J{t}^2\end{array}$$
因此可以得到：
$$S={\int }_0^t\frac{1}{2}J{t}^{2}dt=\frac{1}{6}J{t}^3{|}_0^t$$

积分忘的差不多了，回去再复习一下；

最终位移的方程如下所示；

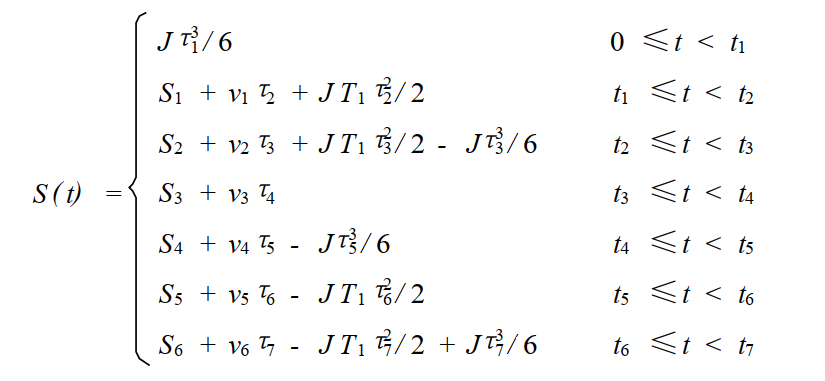
3 程序实现的思路

正如前面所提到的，S曲线规划需要确定三个最基本的系统参数 ：系统最大速度 $v_{max}$ ，最大加速度a_{max} ，加加速度$J$，这样就可以确定这个运行过程。
这里有一个隐性的条件，就是在运行的过程中可以达到最大速度，这样才是完整的7段S曲线，另外这里还有一些中间参数：

• $t_m=\frac{v_{max}}{a_{max}}$，因此有 $T_1=T_3=T_5=T_7$；
• 加加速度 $J=J_1=J_3=J_5=J_7=\frac{a_{max}}{t_m}$；
• $T_2=T_6$；
• $T_f$，用户给定整个运行过程所需要的时间；

但是通常实际过程中关心$a_{max}$，$v_{max}$，$T_f$；

3.1 $T_k$ 推导

理想状态假设存在 $T_2$和$T_6$，则推导过程如下：

$$\{\begin{array}{l}{v}_1=\frac{1}{2}J{T}_1^2\\ v_2=v_1+a_{max}{T}_2\\ v_3=v_2+\frac{1}{2}J{T}_3^2\\ v_3=v_{max}\\ T_1=T_3\end{array}$$

因此可以得到：
$$v_{max}=\frac{1}{2}J{T}_1^2+a_{max}{T}_2+\frac{1}{2}J{T}_1^2$$

简化之后得到：
$$v_{max}=J{T}_1^2+a_{max}{T}_2$$

根据②式可知：$a_{max}=J{T}_1$

最终得到：
$$T_2=T_6=\frac{V_{max}-V_s}{a_{max}}-T_1$$

$V_s为初始速度；$

下面可以根据位移时间关系方程进行离散化的程序编写。

假设可以到达最大速度，且用户给定了整个过程运行时间$T_f$，则 $T_4$ 的推导如下：
$$\{\begin{array}{l}{T}_f=T_1+T_2+T_3+T_4+T_5+T_6+T_7\\ T_2=T_6\\ T_1=T_3=T_5=T_7\end{array}$$
简化上式可以得到：
$$T_4=T_f-2T_2-4T_1$$
根据 $T_1=\frac{a_{max}}{J}$代入上式可得：
$$T_4=T_f-2\frac{v_{max}}{a_{max}}-2\frac{a_{max}}{J}$$

3.2 $J$ 的推导

这时候还剩下$J$需要计算，通过已量 $T_f,v_{max},a_{max}$可以推导出来；
首先位移之间满足关系如下：
$$S_{ref}=S_a+S_4+S_d$$
其中加速区长度为 $S_a$；
其中减速区长度为 $S_d$；
$$\{\begin{array}{l}{S}_a=v_s(2T_1+T_2)+\frac{1}{2}J{T}_1(2T_1^2+3T_1{T}_2+T_2^2)\\ S_d=v_3(2T_5+T_6)-\frac{1}{2}J{T}_5(2T_5^2+3T_5{T}_6+T_6^2)\end{array}$$
具体推导；²
前面提到过$T_1=T_3=T_5=T_7$，$T_2=T_6$，因此在$V_s$=0的时候，则
$$S_a+S_d=v_3(2T_5+T_6)=v_3(2T_1+T_2)\cdots ④$$

这里简单推导一下：
$$\{\begin{array}{l}{S}_4=v_4{T}_4\\ T_4=T_f-(T_1+T_2+T_3+T_4+T_5+T_6)\\ T_1=T_3=T_5=T_7=\frac{a_{max}}{J}\\ T_2=T_6=\frac{V_{max}}{a_{max}}-T_1\\ v_3=V_{max}\\ S_{ref}=S_a+S_4+S_d\end{array}\cdots ⑤$$
根据④，⑤最终简化得到：
$$J=\frac{a_{max}^2{v}_{max}}{v_{max}{a}_{max}{T}_f-v_{max}^2-S_{ref}{a}_{max}}$$

$T_f$：为运行的总时间
$S_{ref}$：为运行的总路程

详细推导过程如下：
$$S_{ref}=S_a+S_4+S_d=S_4+v_3(2T_1+T_2)$$
因为：
$$v_3(2T_1+T_2)=v_{max}(2T_1+T_2)$$
因为：
$$\begin{gathered} T_2=T_6=\frac{V_{max}-V_s}{a_{max}}-T_1 \\ {T}_1=T_3=T_5=T_7=\frac{a_{max}}{J} \\ {V}_s=0 \end{gathered}$$
所以，简化得到：
$$v_3(2T_1+T_2)=v_{max}(\frac{v_{max}}{a_{max}}+\frac{a_{max}}{J})$$
所以可以得到：
$$\begin{gathered} S_{ref}=S_4+v_{max}(\frac{v_{max}}{a_{max}}+\frac{a_{max}}{J}) \\ {S}_{ref}=v_{max}{T}_4+v_{max}(\frac{v_{max}}{a_{max}}+\frac{a_{max}}{J}) \end{gathered}$$
因为：
$$T_4=T_f-2\frac{v_{max}}{a_{max}}-2\frac{a_{max}}{J}$$
将其代入可以得到：
$$S_{ref}=v_{max}(T_f-2\frac{v_{max}}{a_{max}}-2\frac{a_{max}}{J})+v_{max}(\frac{v_{max}}{a_{max}}+\frac{a_{max}}{J})$$
简化得到最终结果：
$$J=\frac{a_{max}^2{v}_{max}}{v_{max}{a}_{max}{T}_f-v_{max}^2-S_{ref}{a}_{max}}$$

4 matlab 程序

matlab程序亲测可以运行，做了简单的修改，
因为这里直接给定了整个运行过程的时间，所以需要在SCurvePara函数中求出加加速度 $J$ 的值，路程$S$为 1：

SCurvePara

 function [Tf1,V,A,J,T] = SCurvePara(Tf, v, a)
 T = zeros(1,7);
for i=1:1000
    % 加加速度 J
    J = (a^2 * v) / (Tf*v*a - v^2 - a);
    % Tk
    T(1) = a / J;
    T(2) = v / a - a / J; % t2 = v / a - t1;
    T(3) = T(1);
    T(4) = Tf - 2 * a / J - 2 * v / a;    % t4 = Tf - 4*t1 - 2*t2;
    T(5) = T(3);
    T(6) = T(2);
    T(7) = T(1);
    % 根据T2和T4判断S曲线的类型
    if T(2) < -1e-6
        a = sqrt(v*J);
        display('t2<0');
    elseif T(4) < -1e-6
        v = Tf*a/2 - a*a/J;
        display('t4<0');
    elseif J < -1e-6
        Tf = (v^2 + a) / (v*a) + 1e-1;
        display('J<0');
    else
        break;
    end
end

 A = a;
 V = v;
 Tf1 = Tf;
 end

SCurveScaling

 function s = SCurveScaling(t,V,A,J,T,Tf)
% J = (A^2 * V) / (Tf*V*A - V^2 - A);
% T(1) = A / J;
% T(2) = V / A - A / J; % T(2) = V / A - T(1);
% T(3) = T(1);
% T(4) = Tf - 2 * A / J - 2 * V / A;    % T(4) = Tf - 4*T(1) - 2*T(2);
% T(5) = T(3);
% T(6) = T(2);
% T(7) = T(1);
%%
if (t >= 0 && t <= T(1))
    s = 1/6 * J * t^3;
elseif (  t > T(1) && t <= T(1)+T(2) )
    dt = t - T(1);
    s = 1/2 * A * dt^2 + A^2/(2*J) * dt...
        + A^3/(6*J^2);
elseif ( t > T(1)+T(2) && t <= T(1)+T(2)+T(3) )
     dt = t - T(1) - T(2);
     s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
         + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t > T(1)+T(2)+T(3) && t <= T(1)+T(2)+T(3)+T(4) )
     dt = t - T(1) - T(2) - T(3);
     s = V*dt ...
         +  (-1/6*J*T(3)^3) + 1/2*A*T(3)^2 + (A*T(2) + A^2/(2*J))*T(3) + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t > T(1)+T(2)+T(3)+T(4) && t <= T(1)+T(2)+T(3)+T(4)+T(5) )
     t_temp = Tf - t; 
     dt = t_temp - T(1) - T(2);
     s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
         + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
     s = 1 - s;
elseif ( t > T(1)+T(2)+T(3)+T(4)+T(5) && t <= T(1)+T(2)+T(3)+T(4)+T(5)+T(6) )
     t_temp = Tf - t; 
     dt = t_temp - T(1);
     s = 1/2 * A * dt^2 + A^2/(2*J) * dt + A^3/(6*J^2);
     s = 1 - s;  
elseif ( t > T(1)+T(2)+T(3)+T(4)+T(5)+T(6) && t <= T(1)+T(2)+T(3)+T(4)+T(5)+T(6)+T(7) + 1e5 )
     t_temp = Tf - t; 
     s = 1/6 * J * t_temp^3;
     s = 1 - s;     
end
 
end

测试的代码如下：
TEST

%%
N = 500;

ThetaStart = 0; %起始位置
ThetaEnd = 90;	%最终位置
VTheta = 90;    %1 		速度
ATheta = 135;   %1.5  	加速度
Tf = 1.8;		% 总行程时间

v = VTheta/(ThetaEnd - ThetaStart);
a = ATheta/(ThetaEnd - ThetaStart);
v = abs(v);
a = abs(a);


Theta = zeros(1,N);
s = zeros(1,N);
sd = zeros(1,N);
sdd = zeros(1,N);

[TF,V,A,J,T] = SCurvePara(Tf, v, a);
display(J, 'J:');
display(TF,'Tf:');
display(V,'v:');
display(A, 'da:');

display(TF-Tf,'dTf:');
display(V-v,'dv:');
display(A-a, 'da:');

t=linspace(0,TF,N);
dt = t(2) - t(1);
for i = 1:N
    if i == N
        a = a;
    end
    s(i) = SCurveScaling(t(i),V,A,J,T,TF);
    Theta(i) = ThetaStart + s(i) * (ThetaEnd - ThetaStart);
    if i>1
        sd(i-1) = (s(i) - s(i-1)) / dt;
    end
    if i>2
        sdd(i-2) = (sd(i-1) - sd(i-2)) / dt;
    end
end

subplot(3,1,1);
legend('Theta');
xlabel('t');
subplot(3,1,1);
plot(t,s)
legend('位移');
xlabel('t');
title('位置曲线');

subplot(3,1,2);
plot(t,sd);
legend('速度');
xlabel('t');
title('速度曲线');

subplot(3,1,3);
plot(t,sdd);
legend('加速度');
xlabel('t');
title('加速度曲线');

看到最终仿真结果和预期相同；

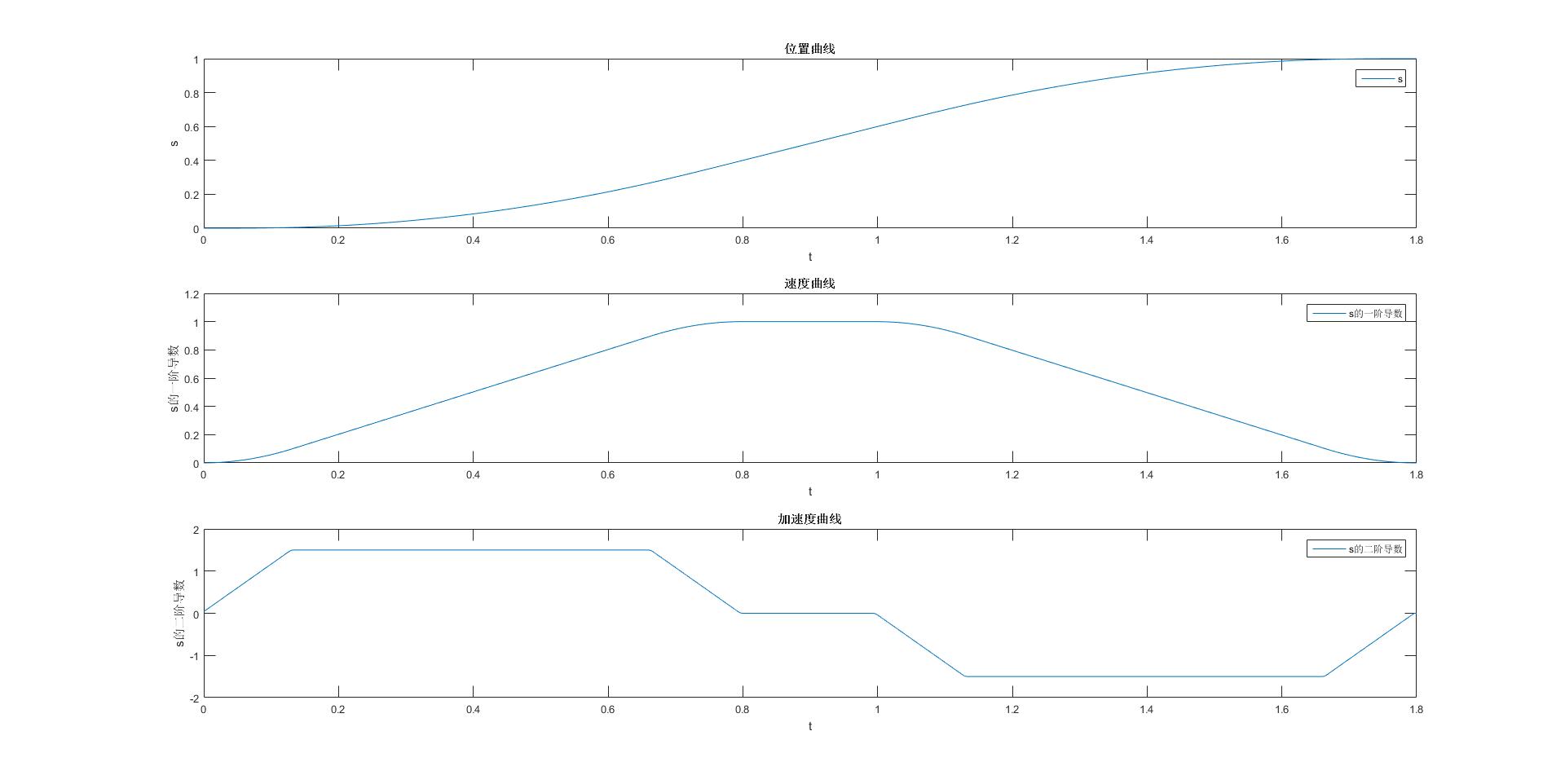
5 总结

本文只对7段的S曲线规划做了详细的推导和介绍，matlab中的程序对于4段和5段都有做实现，很多是在理想情况下进行推导的，初始速度默认为0，终止速度也为0，并且假设加减速区域相互对称。最终运行结果符合预期效果。

文中难免有错误和纰漏之处，请大佬们不吝赐教
创作不易，如果本文帮到了您；
请帮忙点个赞 ????????????；
请帮忙点个赞 ????????????；
请帮忙点个赞 ????????????；

6 参考

最后

以上就是纯情墨镜为你收集整理的一文教你快速搞懂速度曲线规划之S形曲线（超详细+图文+推导+附件代码）的全部内容，希望文章能够帮你解决一文教你快速搞懂速度曲线规划之S形曲线（超详细+图文+推导+附件代码）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。