目录
- 一、度中心性(Degree Centrality)
- 二、特征向量中心性(Eigenvector Centrality)
- 三、Katz中心性(Katz Centrality)
- 四、介数中心性(Betweeness Centrality)
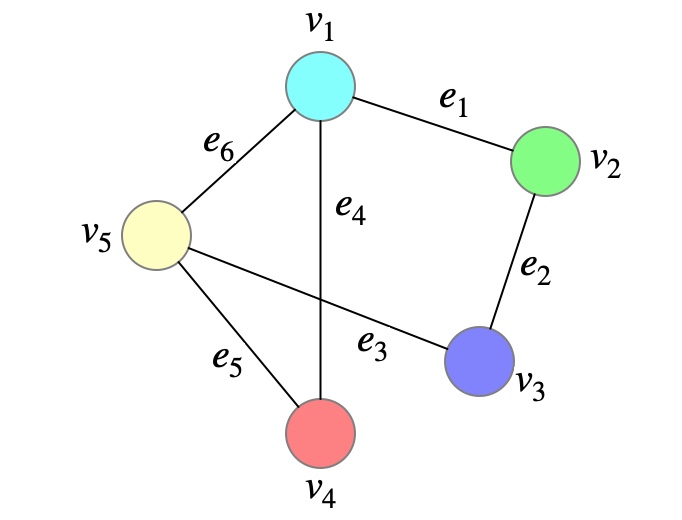
在图中,节点的中心性(Centrality)用于衡量节点在图中的重要性。接下来,以下面这张图的节点为例,介绍一些常用的节点中心性及其计算过程。
一、度中心性(Degree Centrality)
如果有许多其他节点连接到某个节点,那么后者可以被认为是重要的。因此,可以基于一个节点的度测量它的中心性。更具体地说,对于节点
v
i
v_i
vi,其度中心性可以定义为:
c
d
(
v
i
)
=
d
(
v
i
)
=
∑
j
=
1
N
A
i
,
j
c_d(v_i)=d(v_i)=sum_{j=1}^NA_{i,j}
cd(vi)=d(vi)=j=1∑NAi,j
由上面的公式可以知道,节点
v
1
v_1
v1与
v
5
v_5
v5的度中心性都是3,而节点
v
2
v_2
v2、
v
3
v_3
v3和
v
4
v_4
v4的度中心性都是2。
二、特征向量中心性(Eigenvector Centrality)
度中心性认为与多个节点相邻的节点是重要的,且认为所有邻居的贡献度是一样的。然而,这些相邻节点本身的重要性是不同的,因此它们对中心节点的影响不同。给定一个节点
v
i
v_i
vi,特征向量中心性用它的相邻节点的中心性来定义
v
i
v_i
vi的中心性:
c
e
(
v
i
)
=
1
λ
∑
j
=
1
N
A
i
,
j
⋅
c
e
(
v
j
)
c_e(v_i)=frac{1}{lambda}sum_{j=1}^NA_{i,j}{cdot}c_e(v_j)
ce(vi)=λ1j=1∑NAi,j⋅ce(vj) 也可以表达为矩阵的形式:
c
e
(
v
i
)
=
1
λ
A
⋅
c
e
c_e(v_i)=frac{1}{lambda}A{cdot}c_e
ce(vi)=λ1A⋅ce 式中,
c
e
∈
R
N
c_e{in}R^N
ce∈RN是一个包含所有节点的特征向量中心性的向量,这个式子也可以表达为:
λ
⋅
c
e
(
v
i
)
=
A
⋅
c
e
lambda{cdot}c_e(v_i)=A{cdot}c_e
λ⋅ce(vi)=A⋅ce 显然,
c
e
c_e
ce是矩阵的特征向量,
λ
lambda
λ是其对应的特征值。一个邻接矩阵
A
A
A存在多对特征向量和特征值。中心性的值通常为正数,所以选择中心性需要考虑所有元素均为正数的特征向量。根据Perron-Frobenius定理,一个元素全为正的实方阵具有唯一的最大特征值,其对应的特征向量的元素全为正。因此可以选择最大的特征值
λ
lambda
λ,将它的相应的特征向量作为中心性向量。
通过上面的公式进行计算,可以算出示例图中最大的特征值是2.481,对应的特征向量[1, 0.675, 0.675, 0.806, 1]。因此,
v
1
,
v
2
,
v
3
,
v
4
,
v
5
v_1,v_2,v_3,v_4,v_5
v1,v2,v3,v4,v5的特征向量中心性分别是1,0.675,0.675,0.806,1。注意
v
2
v_2
v2、
v
3
v_3
v3和
v
4
v_4
v4的度都是2,但是
v
4
v_4
v4的特征向量中心性比另外两个节点的都要高,因为它和
v
1
v_1
v1、
v
5
v_5
v5两个高特征向量中心性的节点直接相连。
三、Katz中心性(Katz Centrality)
Katz中心性是特征向量中心性的一个变体,它不仅考虑了邻居的中心性,而且包含了一个常数来考虑中心节点本身。具体来说,节点
v
i
v_i
vi的Katz中心性可以定义为:
c
k
(
v
i
)
=
α
∑
j
=
1
N
A
i
,
j
c
k
(
v
j
)
+
β
c_k(v_i)={alpha}sum_{j=1}^NA_{i,j}c_k(v_j)+beta
ck(vi)=αj=1∑NAi,jck(vj)+β 式中,
β
beta
β是一个常数。一个图中所有节点的Katz中心性可以用矩阵形式表示为:
c
k
=
α
A
c
k
+
β
(
I
−
α
⋅
A
)
c
k
=
β
c_k={alpha}Ac_k+beta\ (I-{alpha}{cdot}A)c_k=beta
ck=αAck+β(I−α⋅A)ck=β 式中,
c
k
∈
R
N
c_k{in}R^N
ck∈RN表示所有节点的Katz中心性的向量;
β
beta
β表示一个包含所有节点的常数项
β
beta
β的向量;
I
I
I表示单位矩阵。值得注意的是,如果令
α
=
1
λ
m
a
x
{alpha}=frac{1}{lambda_{max}}
α=λmax1和
β
=
0
beta=0
β=0,那么Katz中心性等价于特征向量中心性,其中
λ
m
a
x
{lambda}_{max}
λmax是邻接矩阵
A
A
A的最大特征值。
α
alpha
α的选择对于Katz中心性非常关键:大的
α
alpha
α值可能使矩阵
I
−
α
⋅
A
I-{alpha}{cdot}A
I−α⋅A变成病态矩阵,而小的
α
alpha
α可能使中心性变得没有意义,因为它总是给所有节点分配非常相似的分数。在实践中,经常令
α
<
1
λ
m
a
x
{alpha}<frac{1}{lambda_{max}}
α<λmax1,这就保证了矩阵
I
−
α
⋅
A
I-{alpha}{cdot}A
I−α⋅A的可逆性,那么
c
k
c_k
ck可按如下方式计算:
c
k
=
(
I
−
α
⋅
A
)
−
1
β
c_k=(I-{alpha}{cdot}A)^{-1}beta
ck=(I−α⋅A)−1β 令
β
=
1
,
α
=
1
5
beta=1,alpha=frac{1}{5}
β=1,α=51,经过计算可得示例图中节点
v
1
v_1
v1和
v
5
v_5
v5的Katz中心性都是2.16,
v
2
v_2
v2和
v
3
v_3
v3的Katz中心性是1.79,
v
4
v_4
v4的Katz中心性是1.87。
四、介数中心性(Betweeness Centrality)
前面提到的几种中心性基于和相邻节点的连接。另一种度量节点重要性的方法是检查它是否在图中处于重要位置。具体来说,如果有许多路通过同一个节点,那么该节点处于图中的一个重要位置。节点
v
i
v_i
vi的介数中心性的定义如下:
c
b
(
v
i
)
=
∑
v
s
≠
v
i
≠
v
t
σ
s
t
(
v
i
)
σ
s
t
c_b(v_i)=sum_{v_s{neq}v_i{neq}v_t}frac{sigma_{st}(v_i)}{sigma_{st}}
cb(vi)=vs=vi=vt∑σstσst(vi) 式中,
σ
s
t
sigma_{st}
σst表示所有从节点
v
s
v_s
vs到节点
v
t
v_t
vt的最短路的数目(此处不区分
v
s
v_s
vs与
v
t
v_t
vt);
σ
s
t
(
v
i
)
sigma_{st}(v_i)
σst(vi)表示这些路中经过节点
v
i
v_i
vi的路的数目。为了计算介数中心性,需要对所有可能的节点对求和。因此,介数中心性的值会随着图的增大而增大。为了使介数中心性在不同的图中具有可比性,需要对它进行归一化(normalization)。一种有效的方法是将所有节点的中心性除以其中的最大值。由上面介数中心性的公式可知,当任意一对节点之间的最短路都通过节点
v
i
v_i
vi时,介数中心性达到最大值,即
σ
s
t
(
v
i
)
σ
s
t
=
1
,
∀
v
s
≠
v
i
≠
v
t
frac{sigma_{st}(v_i)}{sigma_{st}}=1,{forall}v_s{neq}v_i{neq}v_t
σstσst(vi)=1,∀vs=vi=vt。在一个无向图中,共有
(
N
−
1
)
(
N
−
2
)
2
frac{(N-1)(N-2)}{2}
2(N−1)(N−2)个不包含节点
v
i
v_i
vi的节点对,所以介数中心性的最大值是
(
N
−
1
)
(
N
−
2
)
2
frac{(N-1)(N-2)}{2}
2(N−1)(N−2)。所以
v
i
v_i
vi归一化后的介数中心性
c
n
b
(
v
i
)
c_{nb}(v_i)
cnb(vi)可以定义为:
c
n
b
(
v
i
)
=
2
×
∑
v
s
≠
v
i
≠
v
t
σ
s
t
(
v
i
)
σ
s
t
(
N
−
1
)
(
N
−
2
)
c_nb(v_i)=frac{2{times}sum_{v_s{neq}v_i{neq}v_t}frac{sigma_{st}(v_i)}{sigma_{st}}}{(N-1)(N-2)}
cnb(vi)=(N−1)(N−2)2×∑vs=vi=vtσstσst(vi) 在示例图中,节点
v
1
v_1
v1和
v
5
v_5
v5的介数中心性是
2
3
frac{2}{3}
32,而它们归一化后的中心性是
1
4
frac{1}{4}
41。节点
v
2
v_2
v2和
v
3
v_3
v3的介数中心性是
1
2
frac{1}{2}
21,而它们归一化后的中心性是
1
12
frac{1}{12}
121。节点
v
4
v_4
v4的介数中心性和归一化的中心性均为0。
最后
以上就是酷酷小蝴蝶最近收集整理的关于节点中心性:度中心性、特征向量中心性、Katz中心性、介数中心性的全部内容,更多相关节点中心性内容请搜索靠谱客的其他文章。








发表评论 取消回复