文章目录
- 度中心性(Degree Centrality)
- 特征向量中心性(Eigenvector Centrality)
- Katz中心性(Katz Centrality)
- Katz index
- PageRank中心性
- PageRank算法
- 接近中心性(Closeness Centrality)
- 介数中心性(Betweenness Centrality)
节点中心性是图中衡量节点重要性的重要指标。节点中心性常用于无向图,也可以用于有向图,PageRank和HITS算法常用于有向图。
度中心性(Degree Centrality)
节点的重要性可以从于其他节点之间的连接关系(度)来体现,与许多其他节点连接的点可以被认为是重要的。对于节点vi而言,其度中心性定义为
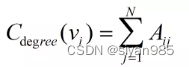
特征向量中心性(Eigenvector Centrality)
度中心性认为所有邻居的贡献度是一样的,但是不同邻居对中心节点的影响应该不同。特征向量中心性的计算不是简单地为每个邻居赋一个值,而是根据该邻居节点所赋的值的和,成正比地为中心节点赋值。
假设对于所有节点的初始值为ci,则将所有邻居节点的中心性之和更新节点的中心性:
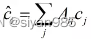
写成矩阵的形式
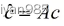
重复t步可以得到很好的估算值
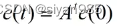
c(0)可以写成邻接矩阵特征向量ai的线性组合即
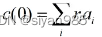
其中r为权重系数,因此,矩阵形式可以重写为
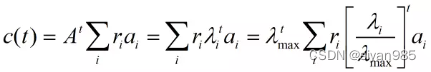
当t趋向于无穷大时,
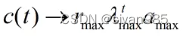
也就是说,中心向量的极限与邻接矩阵的主特征向量成正比。
写成矩阵形式
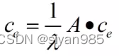
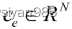
Ce是包含所有节点的特征向量中心性的向量。Ce是邻接矩阵A的特征向量。
换个角度也可以得出相同的结果。因为矩阵A的特征向量有多个,由于中心性通常为正数,因此,需要考虑所有元素值为正数的特征向量。根据Perron-Frobenius定理,一个元素全为正的实方阵具有唯一最大特征值,其对应的特征向量的元素全为正。因此可以选择最大的特征值对应的特征向量作为中心性向量。
给定一个节点vi,特征向量中心性用它的邻居节点的中心性来定义中心节点vi的中心性
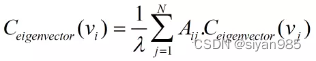
特征向量中心性有个很好的性质就是它的值随两个因素的影响而变大:一是该顶点有很多个邻居;二是该顶点与重要的顶点有之间连接关系。
理论上,特征向量中心性可以应用于有向图和无向图,但无向图效果更好。有向图的邻接矩阵通常是非对称的,这意味着有向图有两类特征向量,也就有两个主向量。一般选择右主特征向量来定义中心性,因为中心性主要是入度节点赋予的,而非中心节点指向的节点。那么就产生了另一个问题就是图中只有出边没有入边的节点中心性便为零。同理,与该节点相连且只有只有这一个入度节点时,当前节点中心性也为零。这样传递下去,只包含中心性为0的节点中心性也同样为0.
Katz中心性(Katz Centrality)
Katz中心性是特征向量中心性的一个变体。为解决特征向量中心性为零的情况,它在特征向量中心性的基础上还为每个节点引入了一个常数项。可使入度为零的顶点有一个中心性β。节点vi的Katz中心性定义为
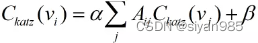
β是常数,写成矩阵的形式
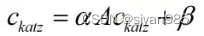
ck表示所有节点的Katz中心性的向量,此处的β表示包含所有节点的β常数项的向量。其中,α的选择对Katz中心性非常关键,如果α等于1/lamda_max,β等于0,则Katz中心性等价于特征向量中心性。Katz中心性的计算方式如下,
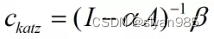
所以常令
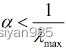
才能保证矩阵(I-αA)可逆。由于不关心中心性的绝对值只关心相对值,因此β的取值并不重要,通常设为β=1。
Katz中心性的一种变体是为不同的节点赋予不同的常数项值。其中βi是每个节点与网络无关的固有中心性。
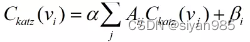
Katz index
局部重叠检测是解决关系预测极其有效的方法,主要计算两个节点共同连接的结点数量。但是局部重叠检测只考虑结点本地的邻居而在一个社区内两个结点很有可能没有重叠结点(没有一阶公共邻居),因此需要从更广的角度来考虑这种关系。
Katz索引(指数)是最基本的全局重叠统计量,计算一对结点之间在整个图中的各种长度的路径的加权和,可用以表示结点间的相似度。
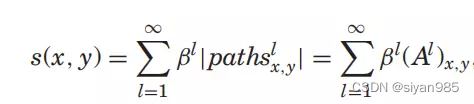
矩阵形式
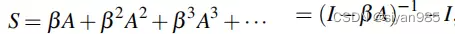
其中,A是邻接矩阵,l是路径长度,β是衰减系数。为了保证数列的收敛性, β 的取值须小于邻接矩阵 A 最大特征值的倒数。
PageRank中心性
Katz中心性有一个不足点在于被katz中心性高的结点指向的结点也具有较高的Katz中心性。但这并不一定合理,比如,谷歌网页中包含指向某个个人网页的链接,但也包含很多指向其他网页的链接,不能因为谷歌的中心性高就认定它所指向的小网页中心性也高。每个小网页只是谷歌指向的数百万网页中的一个,其重要性会被稀释 。也就是说,被重要结点指向的结点从重要结点处获得的中心性因与其他结点共享而被稀释。因此,可以在pagerank中心性中,从邻居结点获得的中心性与邻居结点的中心性除以其出度的结果成正比
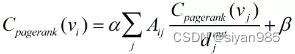
这里要求出度d_out需要大于0,一般对出度为零的结点都把出度设置为1.
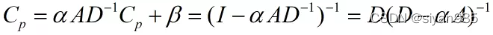
Pagerank的变体中也可以不考虑常数项。
PageRank算法
PageRank算法的基本思想是网络上的一个页面的重要性取决于指向它的页面的数量和质量。一般用于有向图。

从网路上随机游走的观点解释PageRank算法:首先,随机选择一个初始结点,然后每次都从当前节点出发,从该节点指出的边中随机选择一条边并沿此边到达下一节点。可以证明,随机游走k步后位于节点i的概率等于PageRank算法k步后所得节点i的PR值。但是,该方法有个问题就是一旦到达某个出度为零的节点,就会永远停留此处。对于出度为零的节点称作悬挂节点。这些节点会使PageRank算法失效。解决出度为零节点问题的一种方法是给出度为零的节点赋值1/N的概率随机访问任意一个节点。
PageRank算法另一个问题是收敛性的问题,即便网络中没有出度为零的节点且网络全联通,也会出现无法收敛的问题,比如环状图。为了解决收敛问题的有效方法是从当前页面出发,不管该页面是否为出度为零的页面,都予以一定概率随机选取网络中任意节点作为下一节点来访问。如果当前页面出度大于零,则以概率s在当前节点的邻接节点中随机选取作为下一个节点,以1-s的概率在整个图上随机选取下一个节点;如果当前节点出度为零,则在整个图上随机选下一个节点。
修正后的算法如下

PersonalRank算法又称Personalized PageRank算法。该算法继承了经典PageRank算法的思想,利用图链接结构来递归计算各节点的重要性。与PageRank算法不同的是,为了保证随机行走中各节点的访问概率能够反映出用户的偏好,PersonalRank算法在随机行走中的每次跳转会以(1-alpha)的概率返回到源节点,因此可以基于源节点个性化地计算网络节点的相关性和重要性。(PersonalRank值越高,源节点的相关性/重要性越高)。
接近中心性(Closeness Centrality)
接近中心性提供一种完全不同的中心性度量方法,用于度量一个顶点到其他顶点的平均距离。对于网络中每一个节点i,假设该节点到网络中所有节点距离的平均值为di,则:
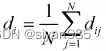
di的值越小意味着节点i更加接近其他节点,因此,它在某种程度上反映了节点在网络中的重要性。我们把的倒数定义为节点的接近中心性,用来表示:
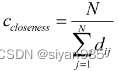
介数中心性(Betweenness Centrality)
常见的中心性是根据邻居节点的连接关系来定义的,还有一种度量节点重要性的方法是通过判断节点在其他节点之间路径上的分布程度。该方法度量一个顶点介于其他顶点的程度。比如,图中很多路径都通过某个节点,那么这个节点就处于重要位置。一个节点的重要性与过该点的路径数成正比。节点vi的介数中心性定义为
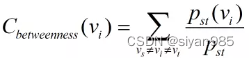
Pst表示所有从节点vs到vt的最短路径数目;Pst(vi)表示这些路径中经过节点vi的路径数目。由于介数中心性需要对所有可能的节点对求和,因此介数中心性的值会随着图的规模增大而增大。因此,需要归一化来使的不同图的介数中心性可比。一种有效的方法是将所有节点的中心性除以其中的最大值。
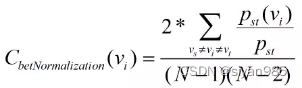
最后
以上就是糊涂翅膀最近收集整理的关于节点中心性的全部内容,更多相关节点中心性内容请搜索靠谱客的其他文章。








发表评论 取消回复