组合逻辑电路

特点

1. 从功能上，任意时刻的输出仅取决于这一时刻的输入
2. 从电路结构上，不含记忆（储存）原件

描述

逻辑函数，传输延迟时间

设计方法

1.逻辑抽象

• 分析因果关心，确定输入/输出变量
• 定义逻辑状态的含义（赋值）
• 列出真值表

2. 写出函数式
3. 选定器件类型
4. 根据所选器件：逻辑式化简（用门），变换（用MSI），或进行相应的描述（PLD）
5. 画出逻辑电路图，或下载到PLD

常用组合逻辑电路模块

编码器

• 将输入的每个高低电平变成一个对应的二进制代码

普通编码器

任何时刻只允许输入一个需要编码的信号（要求很高的物理实现）

例：三位二进制普通编码器（其他无关项是约束项）

优先编码器

允许同时输入两个以上的电平信号，但只对优先权最高的一个进行编码

例：8线-3线优先编码器

实例：74HC148

• ！！再很多器件中都会有一个s，选通端，原因是：这样就可以把这级电路和前面一级电路隔开了，可以使得前端的电路稳定再某个值，对后续电路没有影响

• Ys‘：电路允许工作 无 编码输入

• Yex’：电路允许工作 有 编码输入

• 组合逻辑电路任何时刻的输出都仅取决于该时刻的输入，也就是它永远是一个逻辑表达式的直接实现。

• 组合逻辑电路一定不要有输入到输出的回环

例：两片8-3组成16-4

• 第一片为高优先权
• 只有（1）无编码输入时，（2）才允许工作
• 第（1）片Y‘ex = 0时，表示对A’15-A’8的编码
• 低三位输出应是两片输出的或
• 如果要用两个16-4变成32-5，就要把两个8-3的Y‘ex的或引出来，当作16-4的Y’ex

译码器

• 译码：将每个二进制代码译成对应的输出高低电平信号

• 用二极管实现与门阵列组成3线-8线译码器
  
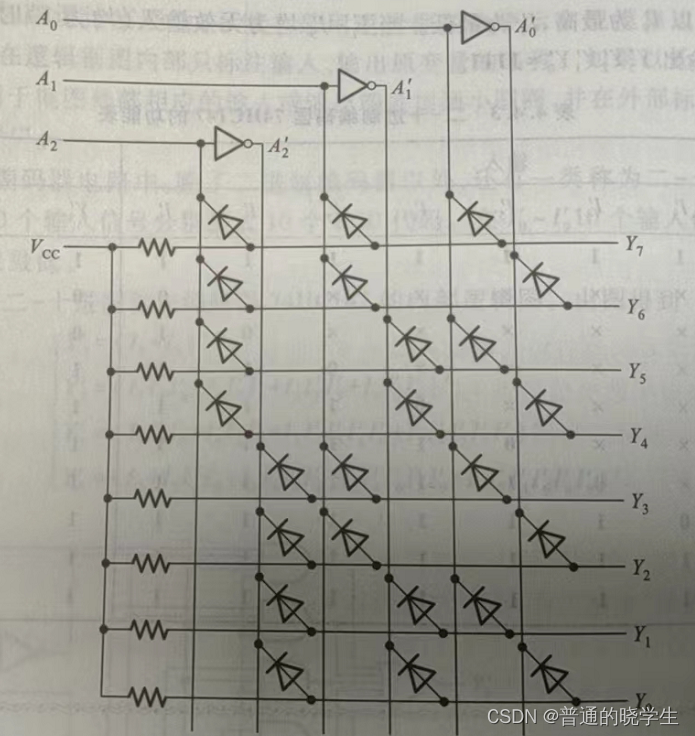
  与阵列：如果把二极管做成活的，如果想让谁完成运算就把二极管跨在他们之间，跨在不同的部位就可以得到不同的与运算。这种思想在大规模集成电路中经常用到。

无关项的概念是我们在设计中为了简化设计而充分利用该逻辑运算物理背景的想法

用译码器实现组合逻辑电路

1. 3位二进制译码器给出了3变量的全部最小项
2. n位二进制译码器给出了n变量的全部最小项
3. 译码器可以当作通用器件来用，因为译码器给出了所有最小项，而逻辑函数又可以表示成最小项之和，只要给够译码器的变量个数，就能相应实现一定规模的组合电路
4. 译码器在实现组合逻辑时，只要外面允许加门，它可以实现多输出，因为最小项可以复用。比如Y0含有最小项m1，Y2也含有m1，这没关系。只要在扇出系数之下都可以用。
5. 删除系数：前端的输出能力驱动够，都可以。不够的时候，直接把它自己扇出两个分支，用树状带下去，从功率上来讲，这时用到的是器件的放大功能。

！数据选择器（MUX）

在大规模数字电路中，它的符号已经和门电路等效

选择端（n）数据端（2的n次方）

数据选择端作为地址，也作为地址分配和数据端一起组合成逻辑式，通过数据选择端的不同取值，决定哪一个数据放在输出上，从而达到单刀多掷的作用。S信号是整个模块的控制端，直接作用与输出端。

用数据选择器设计组合电路

可以设计组合电路，证明数据选择器也可以作为一个通用器件来用。

译出了数据选择端的所有最小项。

三变量的八选一数字选择器，一定可以实现四变量的逻辑函数，因为任意一个逻辑函数，如果n变量的，当它含有2的n-1次方（也就是一半）的最小项时（卡诺图化简，任意一个逻辑函数可以表达成最小项之和，而当他表达成最小项之和的时候，只要多余2的n-1次方，那么就一定可以把有些项和前面的项合并）。三个变量用数据选择端处理，还有一个变量用数据端处理（可能是原变量，反变量。0，1），从根本上来讲，三变量的八选一数字选择器已经具备实现四变量函数逻辑的能力。

对比译码器设计组合逻辑电路：

• 数据选择器要做的工作少
• 缺点：数据选择器是单输出函数，没办法复用

加法器

1. 半加器 ：不考虑来自低位的进位，将两个1位的二进制数相加
2. 全加器：将两个1位二进制数及来自低位的进位相加

！！！多位加法器

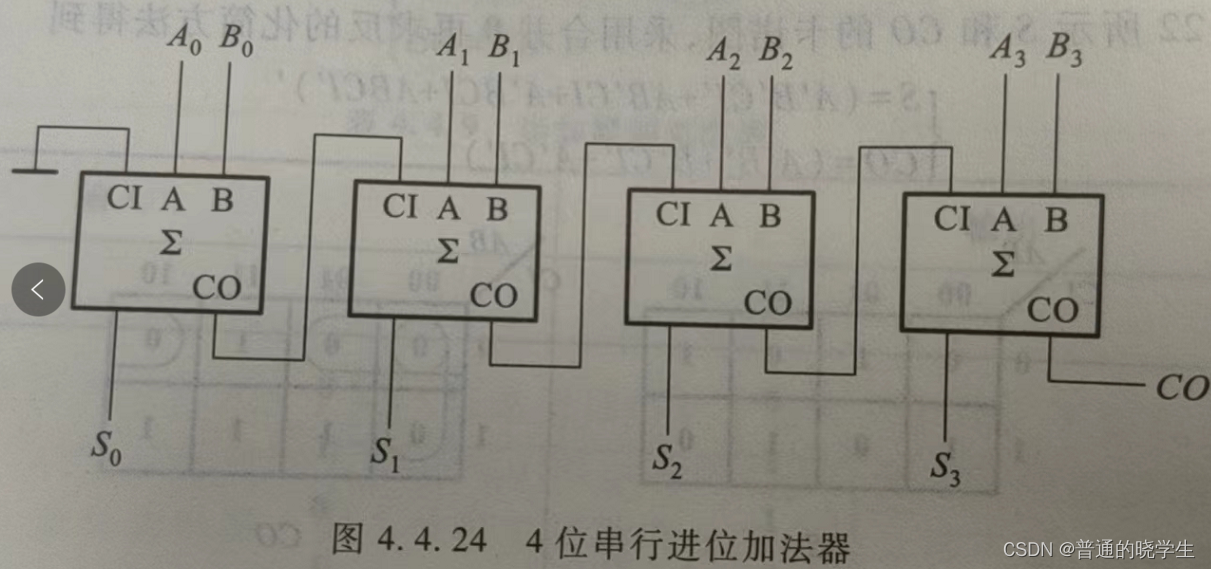
tcd：无效到无效
tpd：有效到有效
！！！！如果用4个全加器串行，当输入给进来之后，隔4倍的每个模块的传输延迟时间，输出才会有变化；而当输入发生变化时，找最短路径，输出就不可信了。这个设计会造成tcd特别短，tpd特别长，所以在电路工作期间，有效电平工作很短。

• ！！！！改进1：前面的设计用了代入定理，S0过了一个传输延迟时间就已经出来了，但是S1要过两个传输延迟，而这时S0不能动，因为是组合电路，输出不能动只能让输入不动。S0是A0，B0的运算，S1是A1，B1和上一模块进位的运算，我们可以不用代入定理，直接展开，S1就变成了A0，B0，A1，B1的运算，就不需要等第一个模块的结果，会变快，但是电路规模会变得很大。（超前进位加法器）

• ！！！！如果一个逻辑运算都可以表达成与或表达的话，基本上三级电路都可以搞定，顶多就是变量取反，再相与，再相或，只要不怕电路麻烦，你的传输延迟时间一定可以控制在某一个扁平化的结构下，但是这样带来的结果是电路规模陡增。

• 改进1速度快，但是复杂，且复用性不好

• 改进2：第五章解决（组合电路解决不了了）

冒险与竞争

1. 竞争：两个输入同时向相反的逻辑电平变化，称存在竞争
2. 因竞争而可能在输出产生尖峰脉冲的现象啊，成为“竞争-冒险”

• 分析法：只要输出在一定条件下可以整理为Y = A + A’ 或 Y = AA’（A和A’之间存在传输延迟时间）
• 观测法：仿真或实际电路

消除方法

1. 接入小的滤波电容（和输出端导通电阻构成一阶RC滤波电路）
2. 引入选通端
3. 修改逻辑设计
   例：Y = AB + AC’，在B=C=1时，Y = A + A’ ，当A改变出现竞争-冒险（因为A传过去一个周期，A’传过去两个周期），这时引入B,C同为一的情况Y = AB + AC’ + BC

！！！！！！！最简不一定最好，卡诺图化简如果出现两个圈相切，就一定有固定的竞争-冒险，解决方式是把相切的地方再圈起来

最后

以上就是无限银耳汤为你收集整理的数电学习（四、组合逻辑电路）组合逻辑电路的全部内容，希望文章能够帮你解决数电学习（四、组合逻辑电路）组合逻辑电路所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。