目录
前言 :
Chapter 1:数字逻辑基础
进制:
进制间转换方法:
BCD:
余3码:
余3循环码:
格雷码(循环码):
二进制数→格雷码(循环码):
格雷码(循环码)→二进制数:
有符号的二进制码:
原码,反码,补码:
负数补码转换成十进制数:
逻辑代数
与,或,非门:
复合逻辑运算:
运算定理:
反演规则:
标准与或式(逻辑函数):
逻辑函数的化简规则:
卡诺图:
二变量卡诺图:
三变量的卡诺图:
四变量的卡诺图:
卡诺图化简举例:
Chapter2:集成逻辑门电路;
概述:
何为门电路?
逻辑门电路的分类:
高低电平与正负逻辑电路:
数字逻辑电路的集成度:
半导体三极管、MOS管、集成TTL门电路和继承CMOS门电路:
半导体三极管的输入输出特性:
MOS管的初步介绍:
集成TTL门电路:
TTL的与非门、或非门、开路门(OC门)、输出三态门:
CMOS介绍:
Chapter 3:组合逻辑电路
概述:
特点:
分类:
分析方法:
逆向分析:
Attention:非的与非→或!!!
组合电路例题分析:
编码器:
译码器:
3 - 8 二进制译码器(高电平有效):
使能端举例:
数码显示器:2 - 10 进制译码器
例题分析:
比较器:
加法器:
1.半加器(Half Adder):
2.全加器(Full Adder):
加法器的级联:
数据的传输方式:
数据分配器:
定义:
1路 - 4路 数据分配器:
数据选择器:
定义:
4路 - 1路 数据选择器(省略逻辑图):
8 路 - 1路 数据选择器:
数据选择器的拓展:
利用数据选择器实现组合逻辑函数:
举例1:
举例2:
奇偶校验器:
8位校验电路举例:
图解原理分析:
PLD:Programmable Logic Device(可编程逻辑器件)
概述:
PLA及其应用:
PAL及其应用:
Chapter 4:集成触发电路和时序逻辑电路
概述
时序电路:任何时刻电路的输出,不仅和该时刻的输入信号有关,还取决于电路原来的状态。
时序电路的分类:
基本触发器:
基本触发器的分类:
基本触发器的原理:
波形图举例:
同步触发器:
同步RS触发器:
D触发器 :
主从触发器:
主从RS触发器:
主从T'触发器:
JK触发器(功能最完善的触发器):
参考资料:
前言 :
本学期开设了电路与电路分析课程,发现在没有足够的知识储备下,想要牢固掌握并理解本课程内容是十分困难的。因此,我决定以写博客的形式复习本课程的数字电路部分。
数字电路部分是本课程内容的第二篇,第一篇是电子器件与电子电路基础,我认为本书和PPT效果非常好,因此将择期更新。
目前,本篇文章更新至第二篇第4章的前半部分,时间仓促,故第二篇剩余内容也择期更新。
如何联系我?
wei.haoran@outlook.com
第二篇 数字电路和系统
Chapter 1:数字逻辑基础
进制:
二进制数优点:电路的两个开关分别表示高低电平,数码的储存和传输简单、可靠;
二进制数缺点:位数较多,使用不便,不符合人们的使用习惯;
进制间转换方法:
1.十进制转换为二进制、八进制、十六进制——连除法;
当十进制数包含小数时,不断地将小数部分乘以要转换的进制,并按其积的正数,依次确定K0,K1······,直到被积数为0;这里举个栗子:
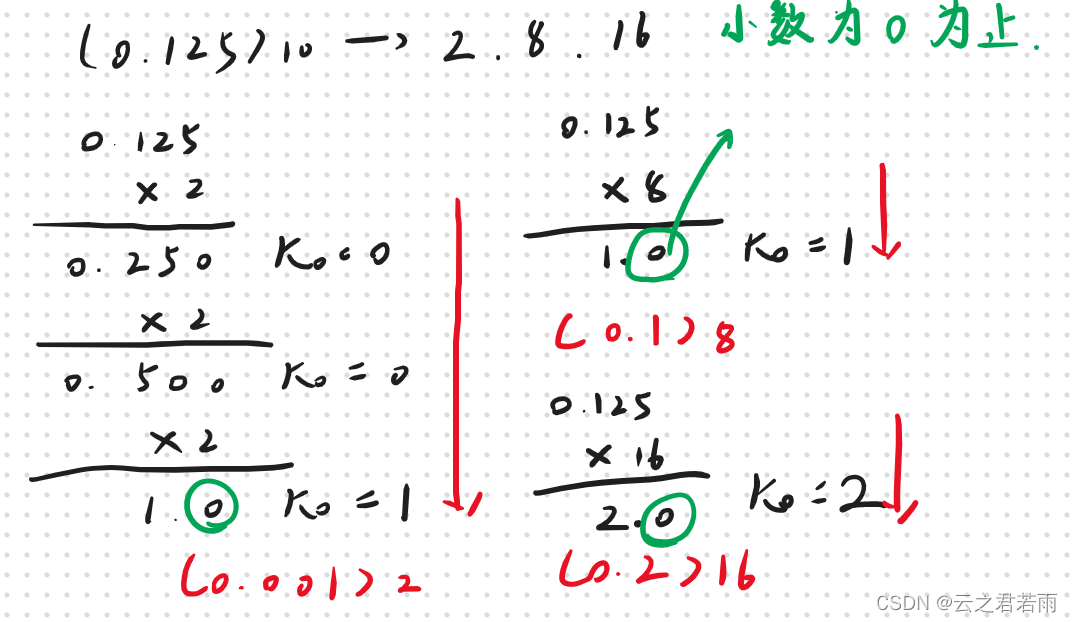
2.二进制、八进制、十六进制的转换:可以以二进制作为桥梁进行转换;
这里的课本和Powerpoint讲解不够精确,因此推荐阅读:
进制转换方法总结—— final__static(CSDN社区)
配套练习及其答案:
计算机各种进制转换练习题(附答案).pdf——明若晓溪(原创力文档)
BCD: 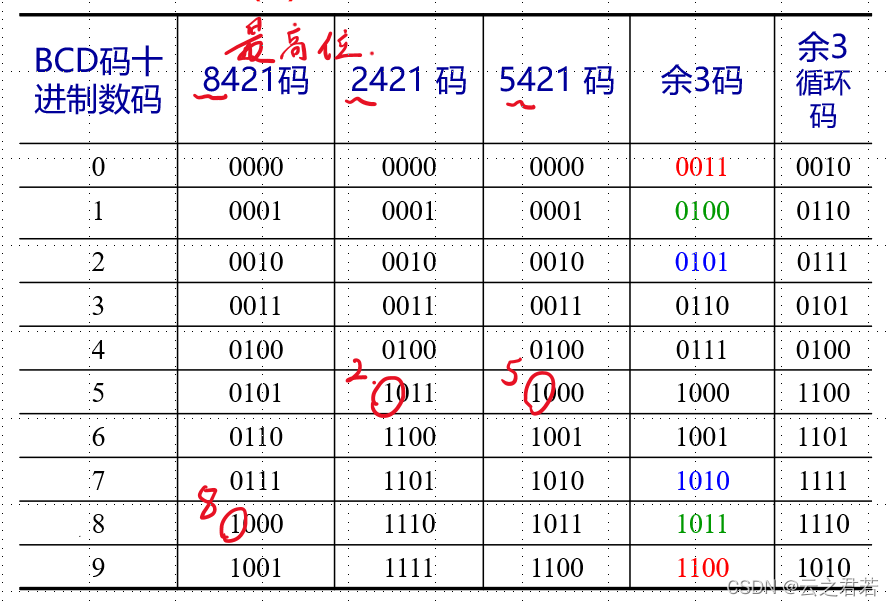
这里要重点掌握8421,2421和5421间的转换;
注意2421码和5421码从十进制数码5开始与8421有区别!
(10010000) 8421BCD=(90)D
(863.2)D=(1110 1100 0011 . 0010)2421BCD = (1011 1001 0011 . 0010)5421BCD
余3码:
推荐阅读:余三码——bidianzhang(CSDN社区)
余3码的每个字符编码均比8421码多3;
余3循环码:
相邻的两个代码之间仅一位的状态不同;按余3码循环码组成计数器时,每次转换过程只有一个触发器翻转,译码时不会发生竞争。
推荐阅读:数字电路——余3循环码—— 寒山有风(CSDN社区)
格雷码(循环码):

由图易知:格雷码任何相邻的字符编码间仅有1位不同,增加了可靠性;
二进制数→格雷码(循环码):
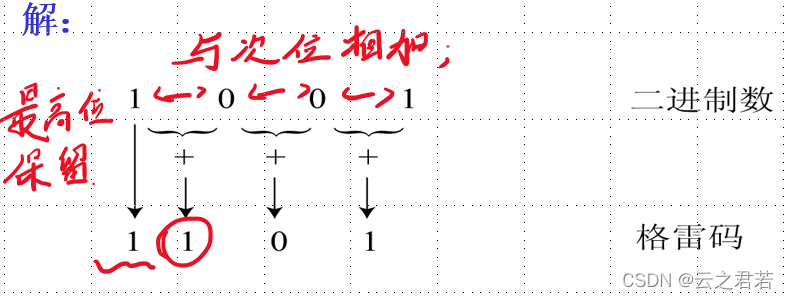
格雷码(循环码)→二进制数: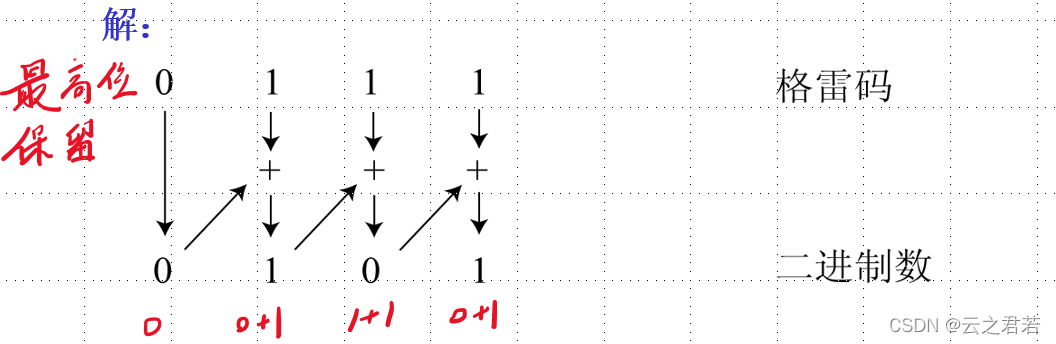
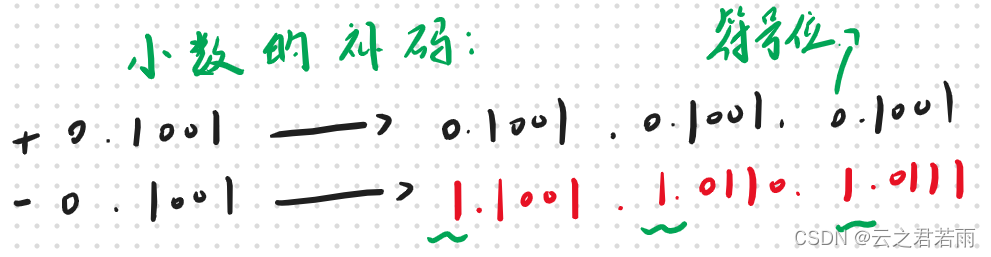
有符号的二进制码:
最高位表示符号位; "0"代表正数,“1”代表负数;
原码,反码,补码:
原码:+33→0 100001; -33→1 100001;
+4.625→0 100.101;-4.625→1 100.101;
反码: +33 →0 100001; 正数的反码原码一致;
-33 →1 011110; 符号位保留,其他位取反;
补码: +33 →0 100001;正数的原码,反码,补码一致;
-33 →1 011111; 负数的补码=其反码 + 1;
补码+补码 = 补码 ,补码的补码 = 原码;
负数补码转换成十进制数:
规则:最高位(符号位)不动, 其余位取反加1(切记:不是减1);
二进制:1 1111001 取反:1 0000110加1:10000111即为:-7;
逻辑代数
与,或,非门:
逻辑符号:
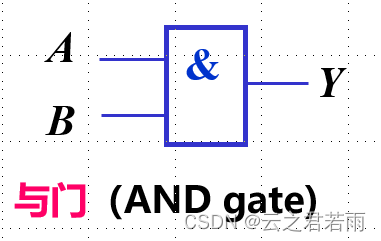
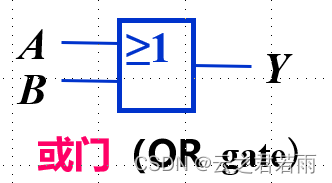
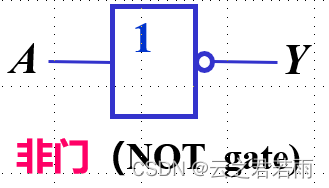
1.用英文字母表示的即为逻辑变量,其值非0即1;
2.原变量:字母头上没有取反符号;反变量:字母头上有取反符号;
3.如果输入逻辑变量 A、B、C ∙ ∙ ∙的取值确定之后,输出逻辑变量 Y 的值也被唯一确定,则称 Y 是 A、B、C ∙ ∙ ∙的逻辑函数。记为:![]()
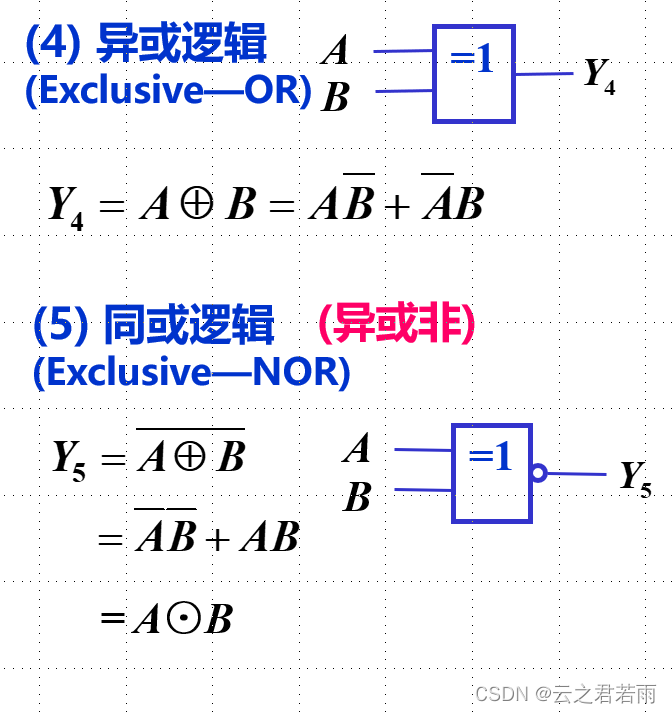
复合逻辑运算:
运算定理:
分配律:
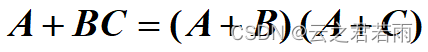
证明方法1:右侧公式通过公式法推出左侧公式;
证明方法2:利用真值表证明二者等价;
德·摩根律:
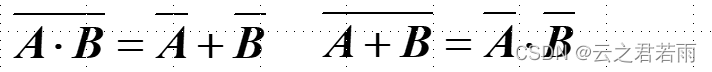
德·摩根律是反演规则的特殊形式;
反演规则:

推荐阅读:数字逻辑中的反演规则和对偶规则——lucifer_zhy(CSDN社区)
举个栗子:

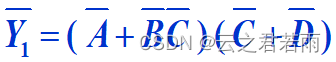
1.作用于多个变量的反号应该保留;
2.运算优先级:括号,与,非;
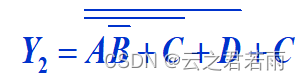
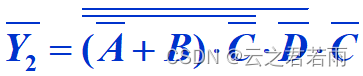
——注意辨析反演规则和德·摩根律,在选定反演规则的情况下,不能同时带有德·摩根律的想法,在选定德·摩根规则的前提下,不能同时带有反演规则,应该严格遵循两种原则的基本规则。
异或的非 = 同或 ; 同或的非 = 异或;
如图:
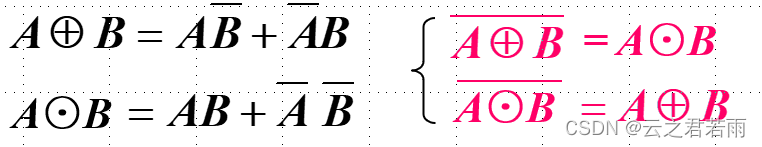
标准与或式(逻辑函数):
定义:标准与或式就是最小项之和的形式;类比离散数学中的主析取范式;
举个栗子:
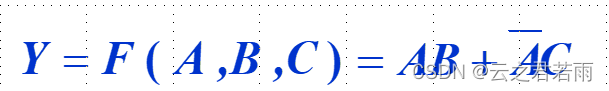
AB缺少变量C,A非C缺少变量B;因此,补上(C + C非);(B + B非);
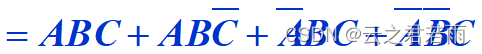 (标准与或式)
(标准与或式)
最小项表格:
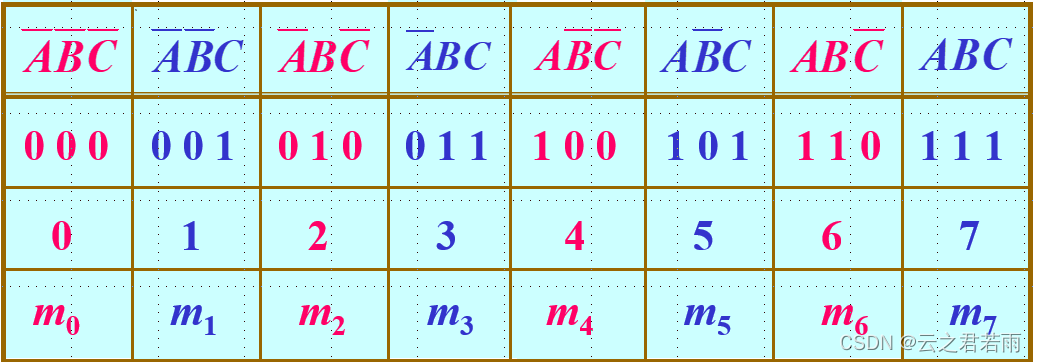
因此,我们可以类比离散数学的最小项,编号表示成真赋值;
Attention:
mi 与 Mi 互为取反。
任何逻辑函数都是由其变量的若干个最小项构成,都可以表示成为最小项之和的形式。
逻辑函数的化简规则:
1.并项法:![]()
2.吸收法:![]()
举个栗子:
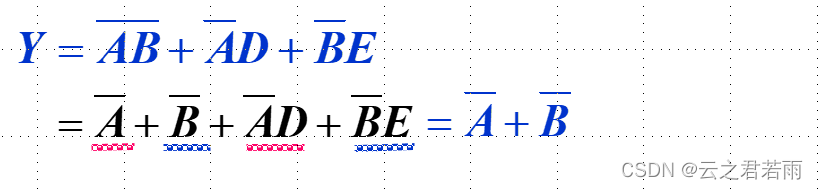
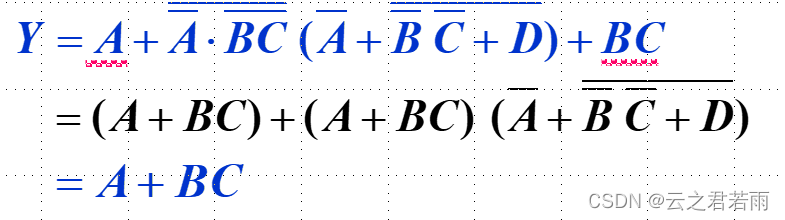 3.消去法:
3.消去法: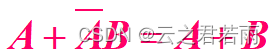
举个栗子:
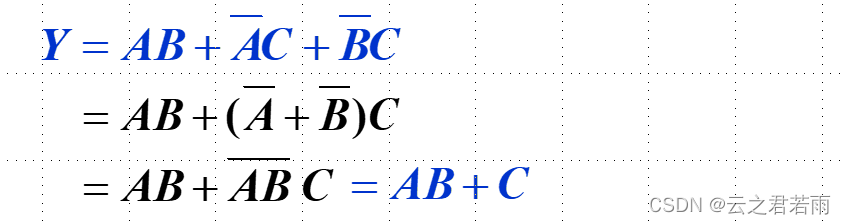 好难???
好难???
卡诺图:
二变量卡诺图:
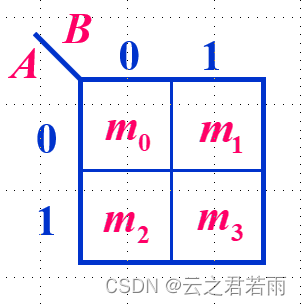
由图易知:
1.图内的元素表示最小项;
2.切记最小项方格图按照循环码排列;
三变量的卡诺图:
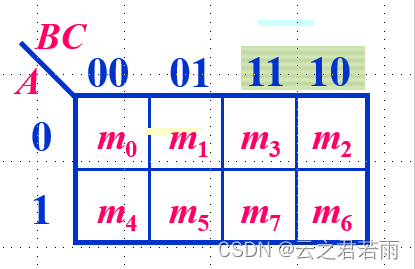
由图可知:逻辑相邻的两个最小项合并,只能消去一个因子;
在几何上,紧挨着的,行或列的两头,对折起来位置重合的,都是几何相邻(逻辑相邻);
四变量的卡诺图:
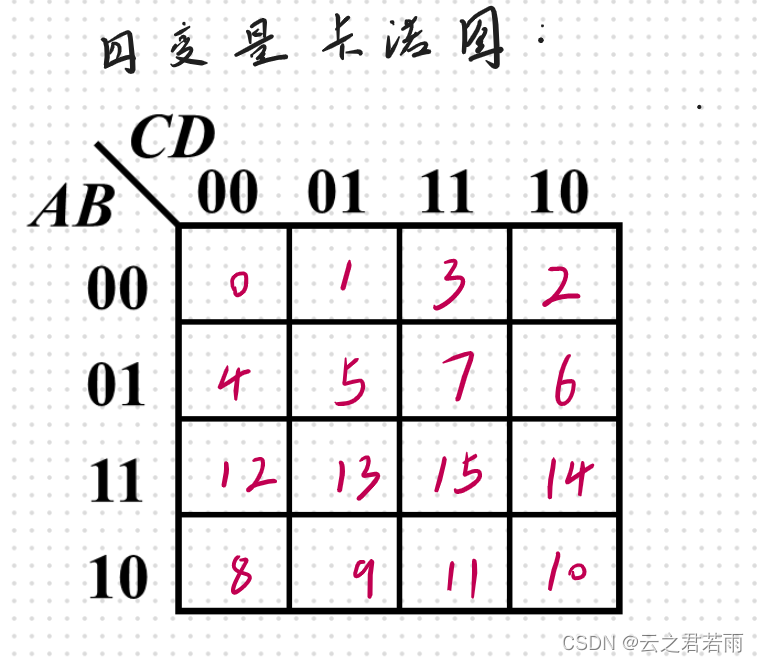
卡诺图化简举例: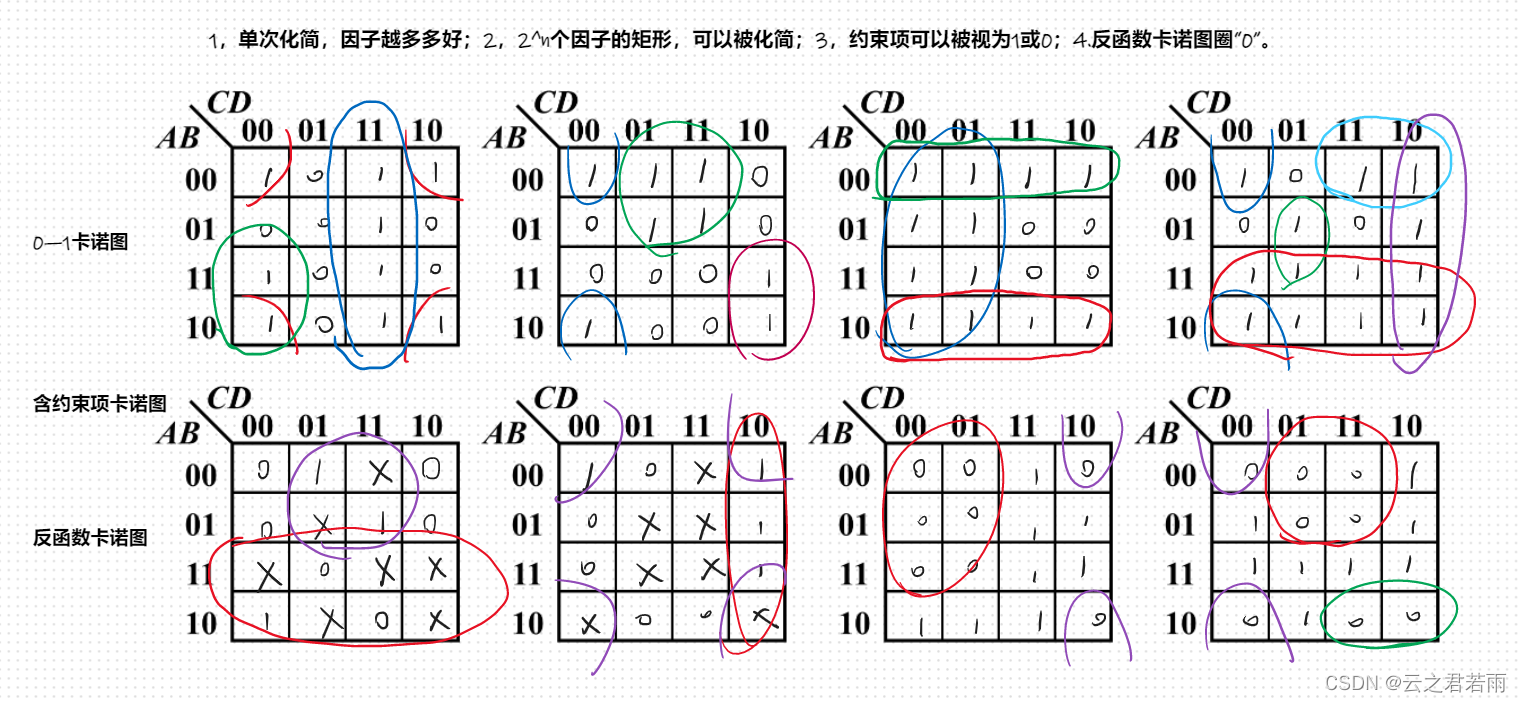
Chapter2:集成逻辑门电路;
概述:
何为门电路?
——实现基本逻辑运算和常用复合逻辑运算的电子电路;
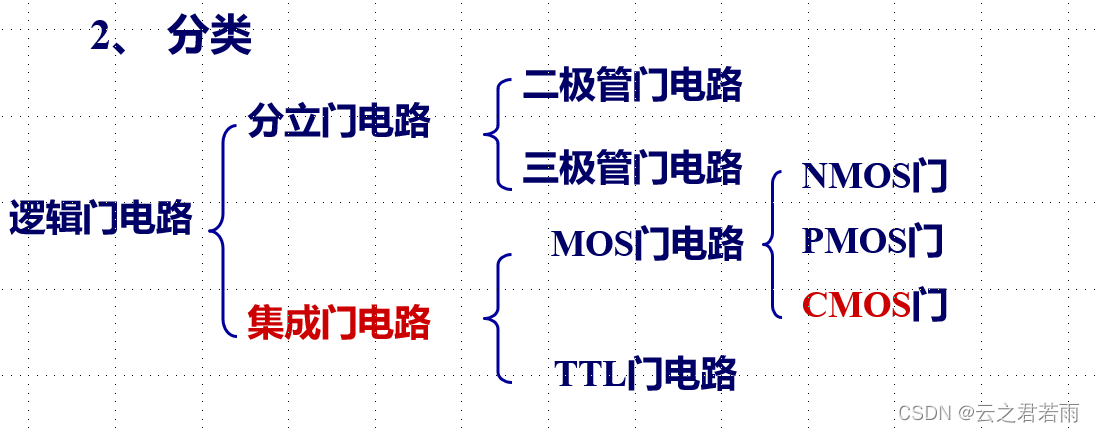
逻辑门电路的分类:
重点介绍集成门电路的MOS门电路的CMOS门;
高低电平与正负逻辑电路:
高电平和低电平可以用正逻辑或负逻辑进行表达;
一般选用正逻辑:2.4~5V 表示 “1”; 0~0.8V 表示 “0”;
数字逻辑电路的集成度:

一般来说,目前我们所研究的是中规模集成电路(MSI);
半导体三极管、MOS管、集成TTL门电路和继承CMOS门电路:
半导体三极管的输入输出特性:
输入特性:
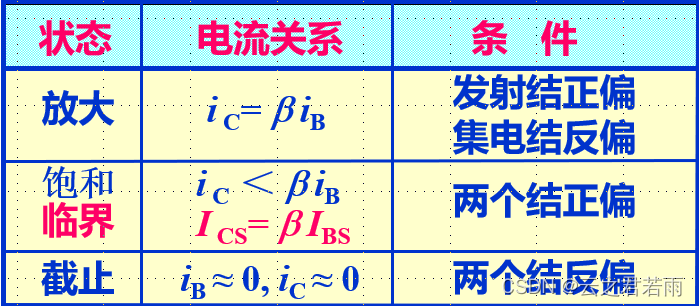
请注意:当发射结反偏,集电结正偏时,半导体三极管处于倒置放大状态,即有:
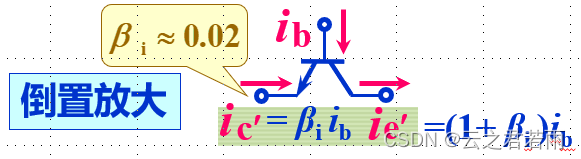
输出特性: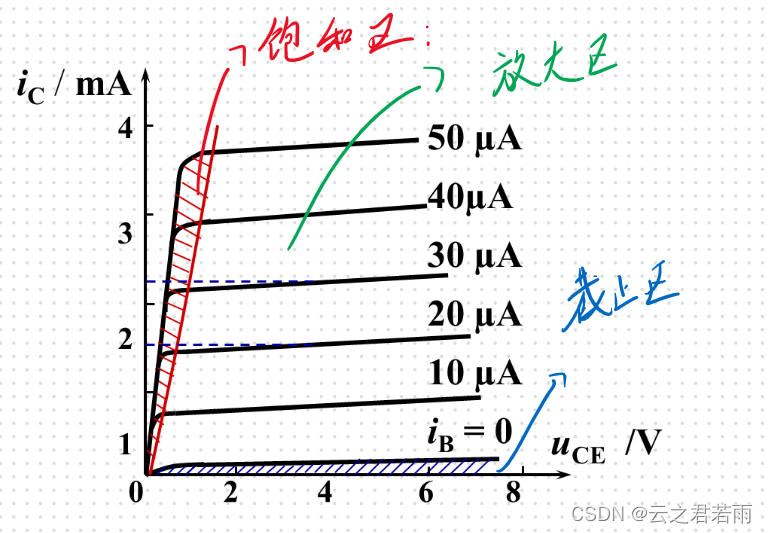
切记:T饱和时,![]() ;
;
注意,当Ib > Ibs 时,T处于饱和状态; Ic = β·Ibs;
MOS管的初步介绍:
有N沟道和P沟道;
N沟道的开启电压:Utn = 2V; 对应于“1”;
P沟道的开启电压:Utn = -2V; 对应于“0”;
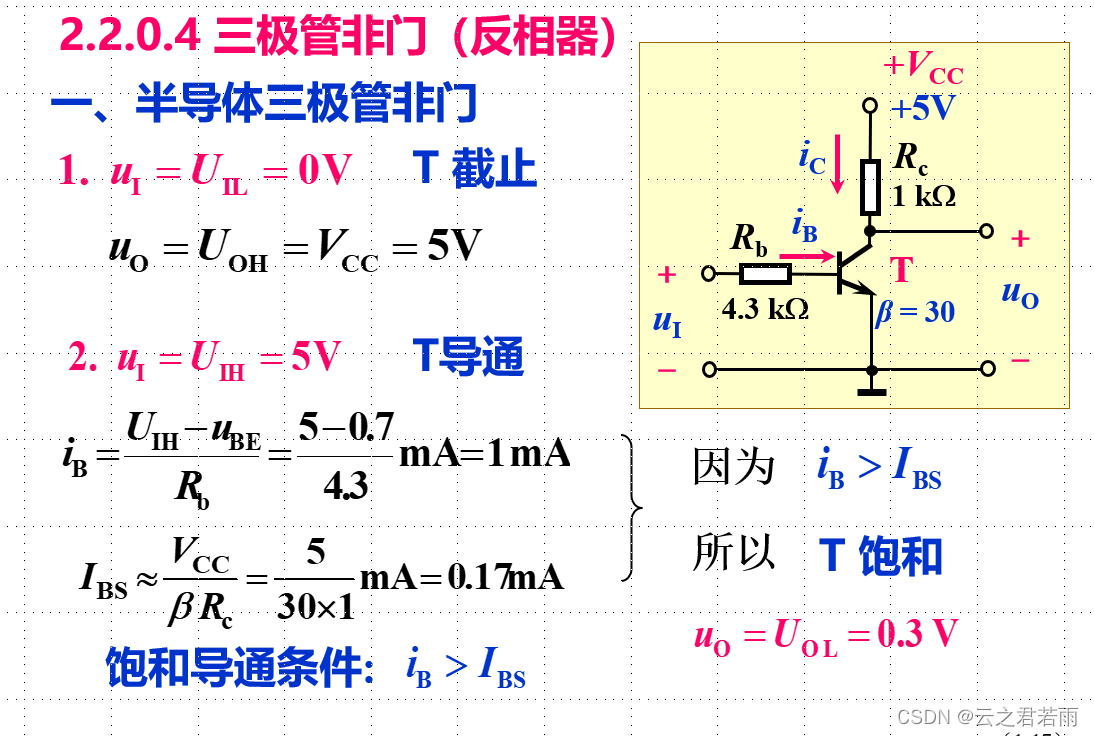
集成TTL门电路:
1.Ui = 0V 时,输出为 3.6V :高电平;
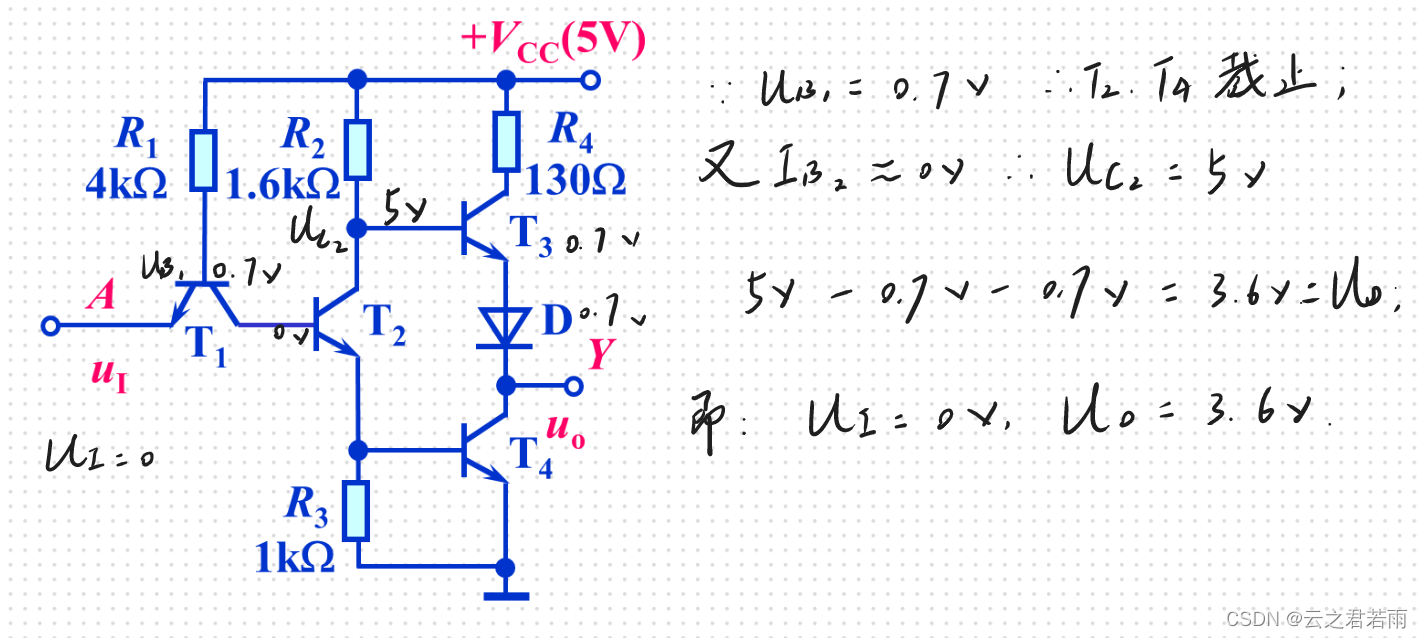
2.Ui = 3.6V 时,输出为0.3V : 低电平;

输出特性曲线:
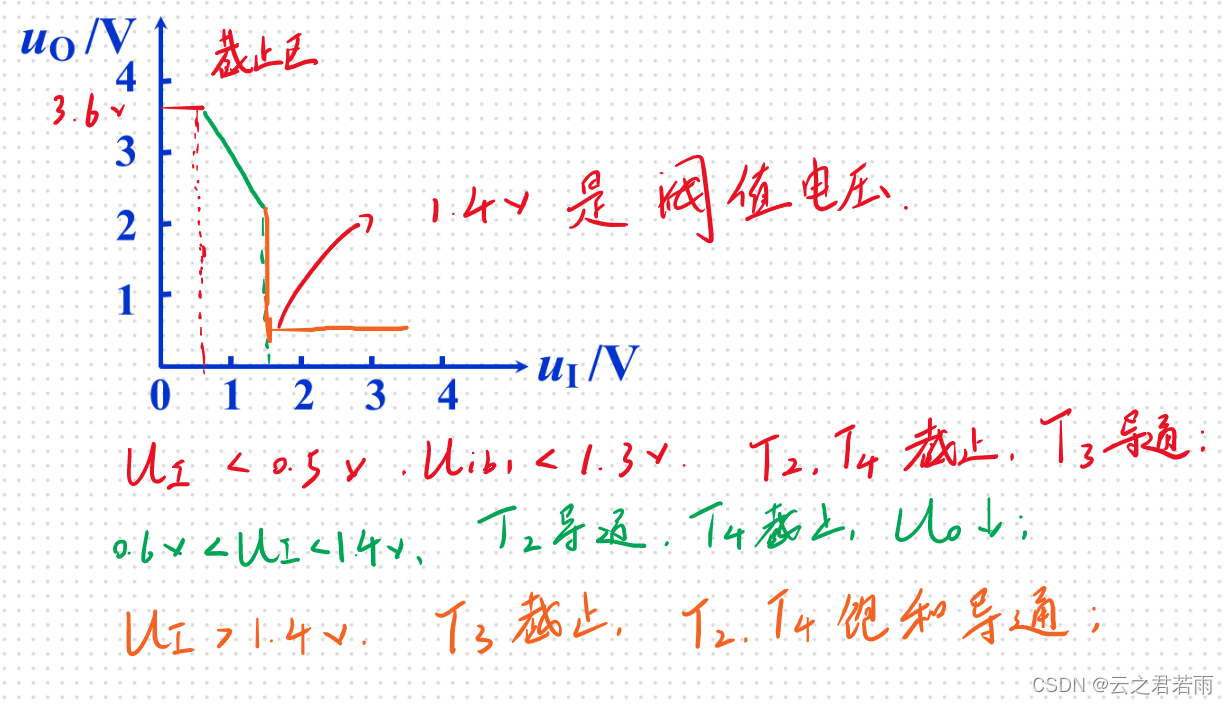
输入端负载特性: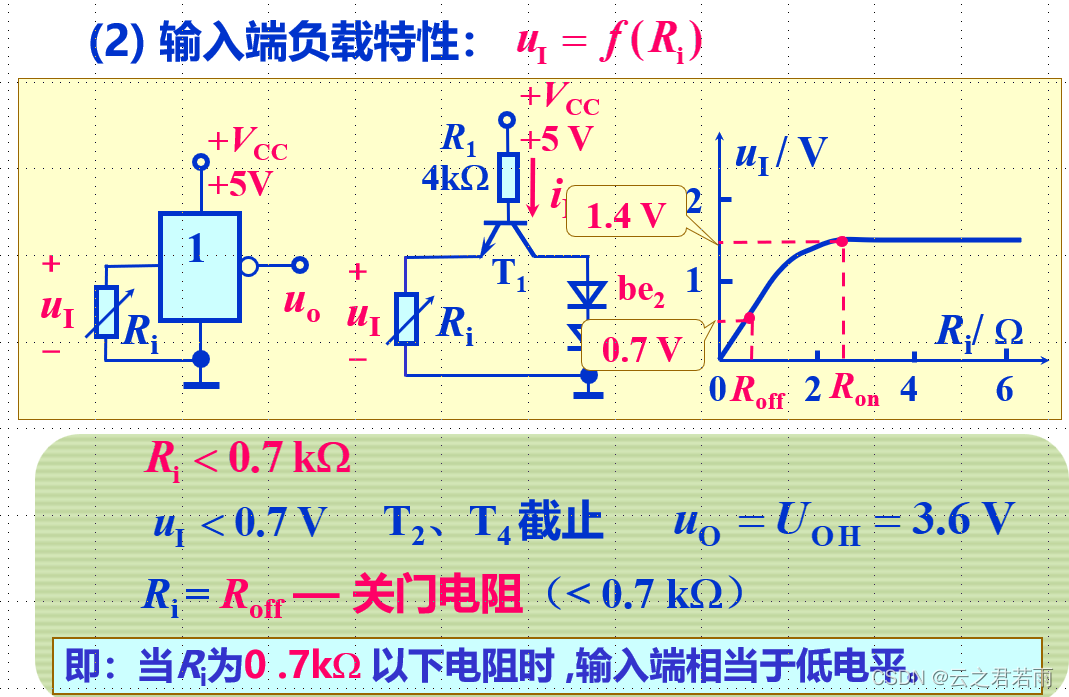
TTL的与非门、或非门、开路门(OC门)、输出三态门:
与非门:
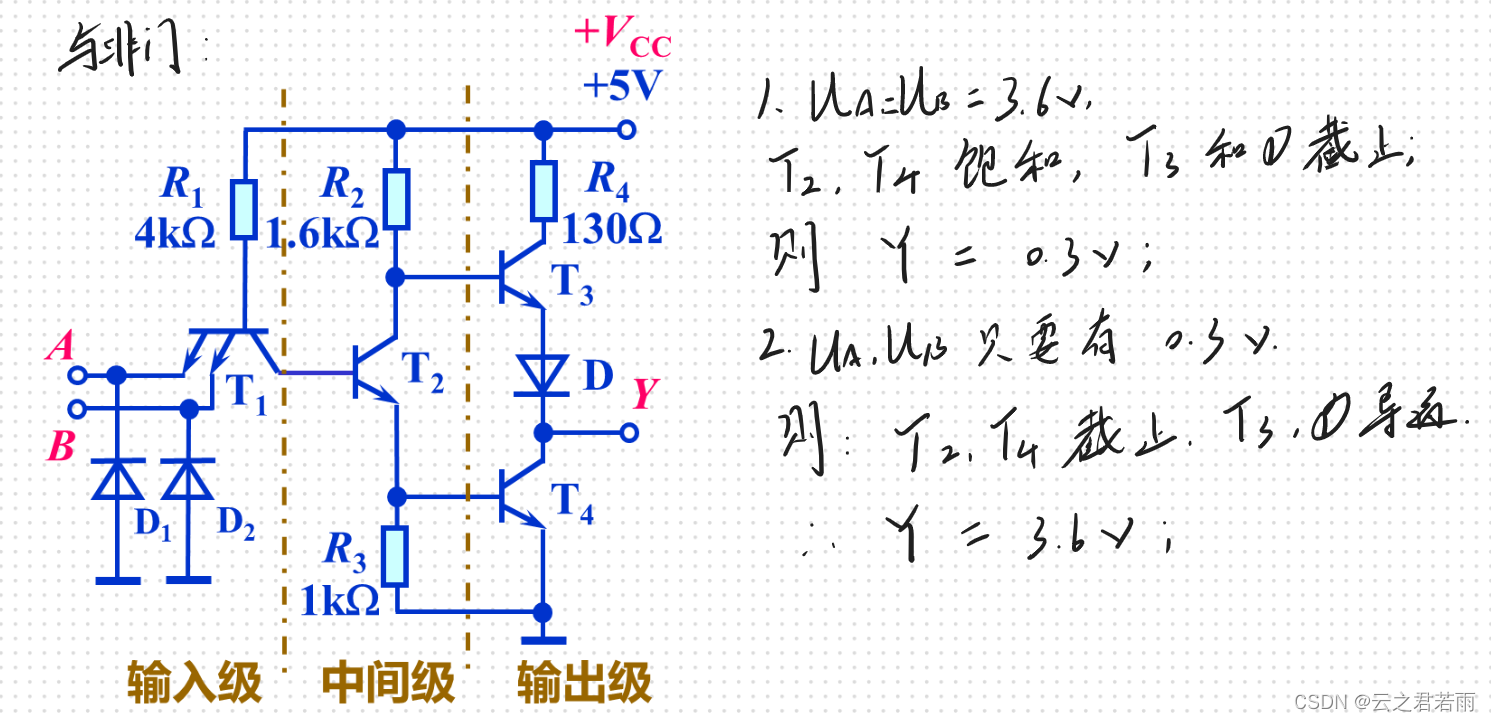
或非门: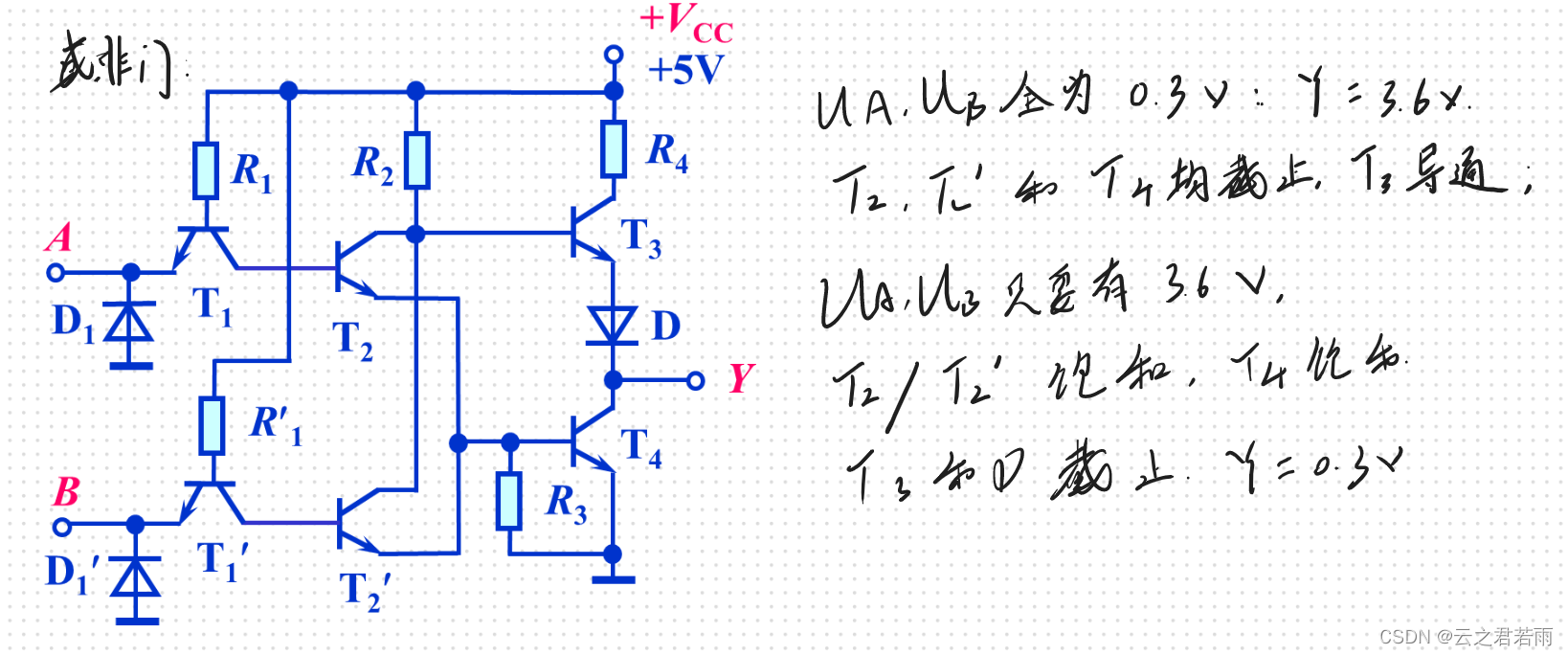
OC门线与实例: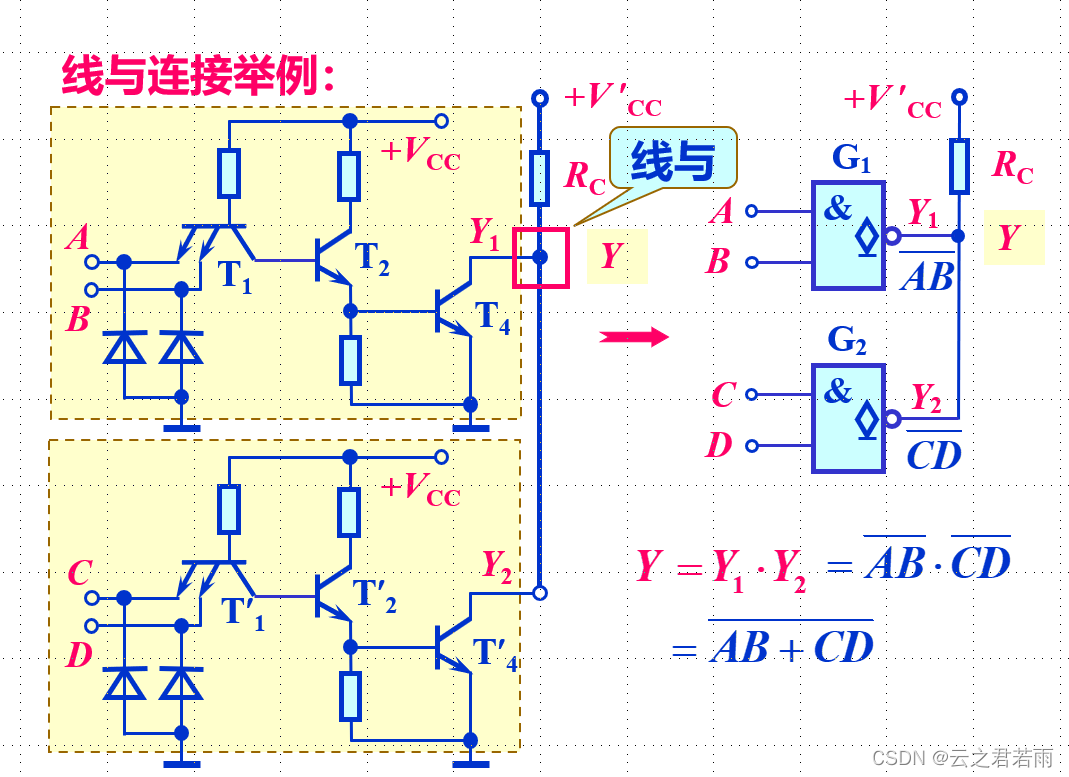
三态门:高阻态(非0非1),0 和 1;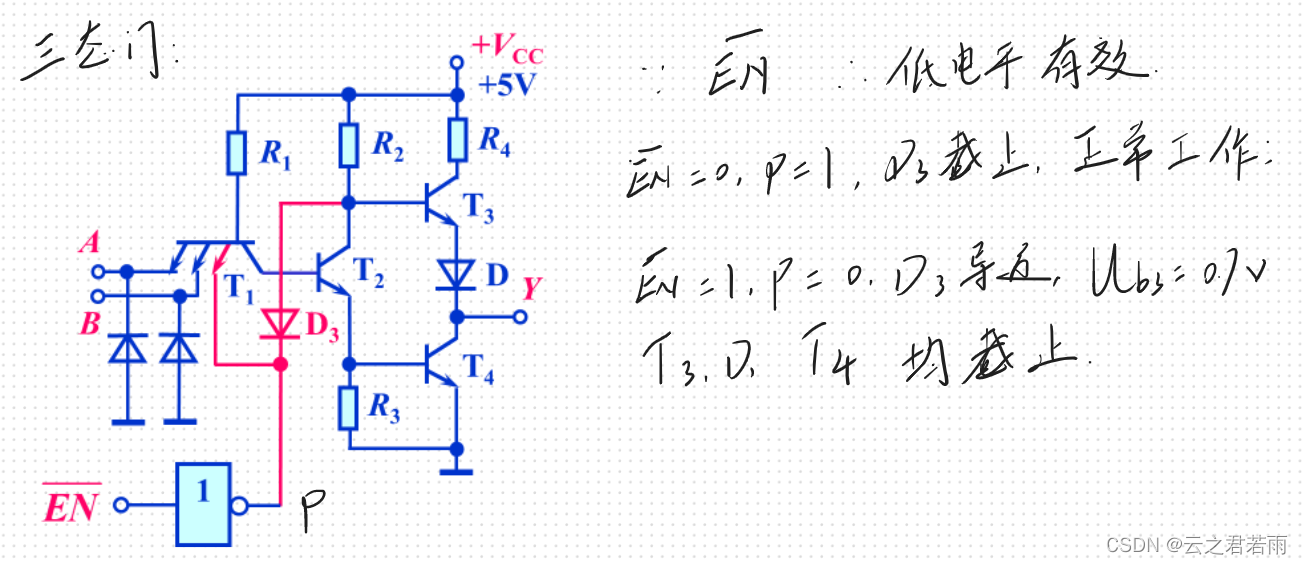
注意:EN 表示输入高电平有效,EN非 表示输入低电平有效;
CMOS介绍:
1.CMOS反相器:
注意:Utn为2V,Utp为 -2V;
则输入为0V时,TN截止,TP导通;输入为3.6V时,TN导通,TP截止;
2.CMOS的与非门和或非门:
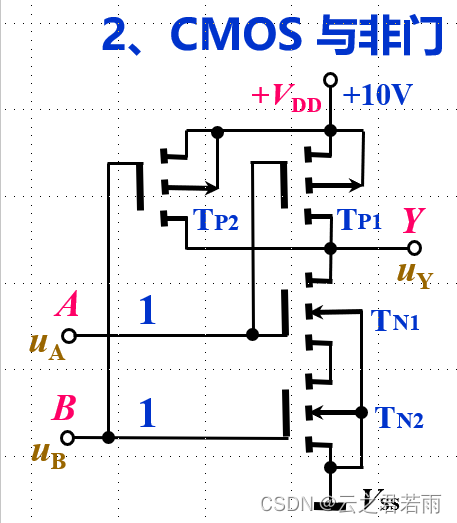
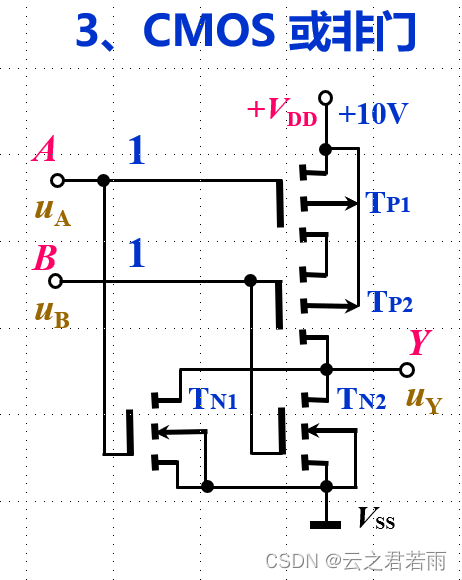
3.CMOS的与门和或门:
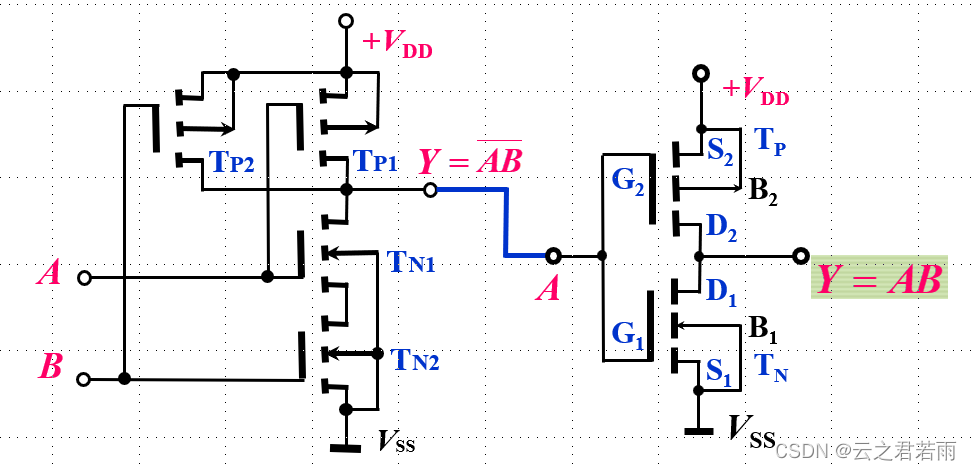
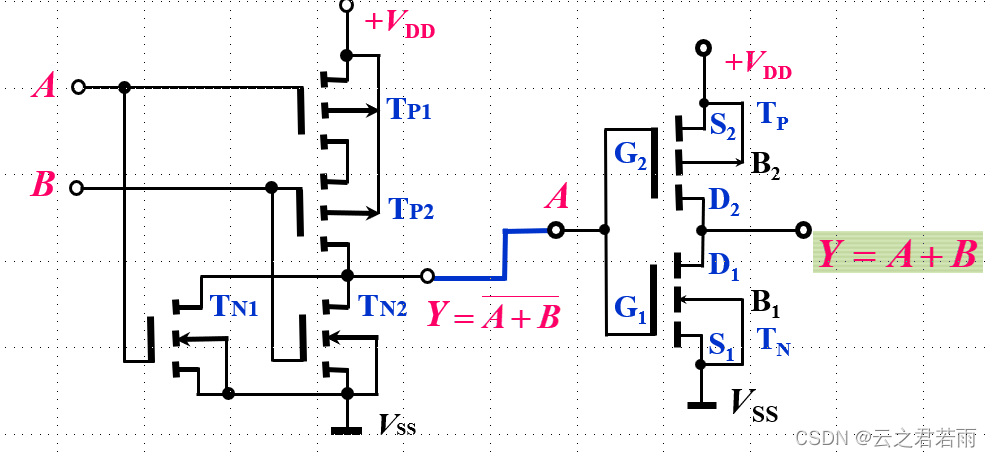
4.CMOS的三态门:
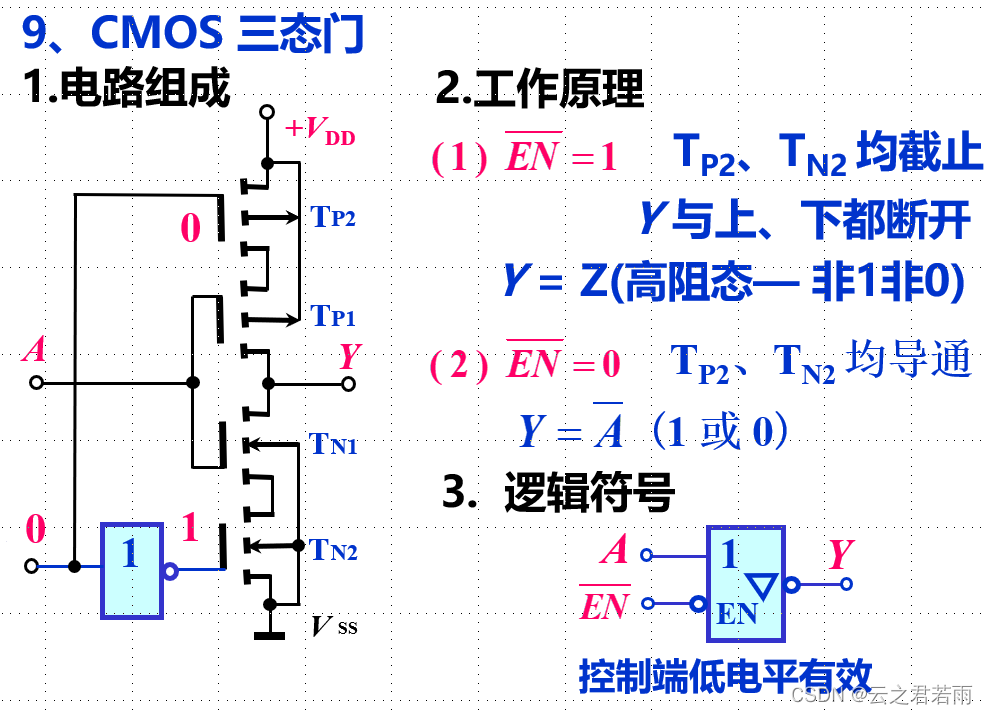
Chapter 3:组合逻辑电路
概述:
-
特点:
- 电路在某时刻的输出态,仅取决于该时刻的输入态,与原态无关
- 输入和输出间无反馈延迟
- 仅由门电路构成
-
分类:
- 逻辑功能:加法器,比较器,编码器,译码器,只读储存器;
- 开关元件:CMOS,TTL;
- 集成度:SSI,MSI,LSI,VLSI;
-
分析方法:
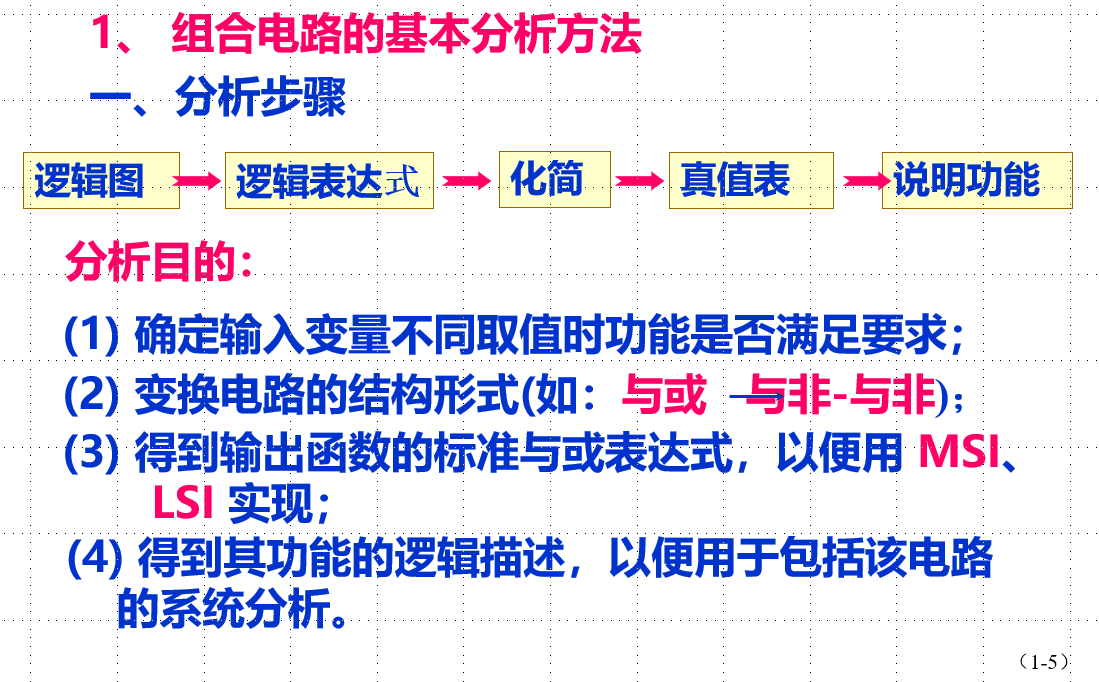
-
逆向分析:
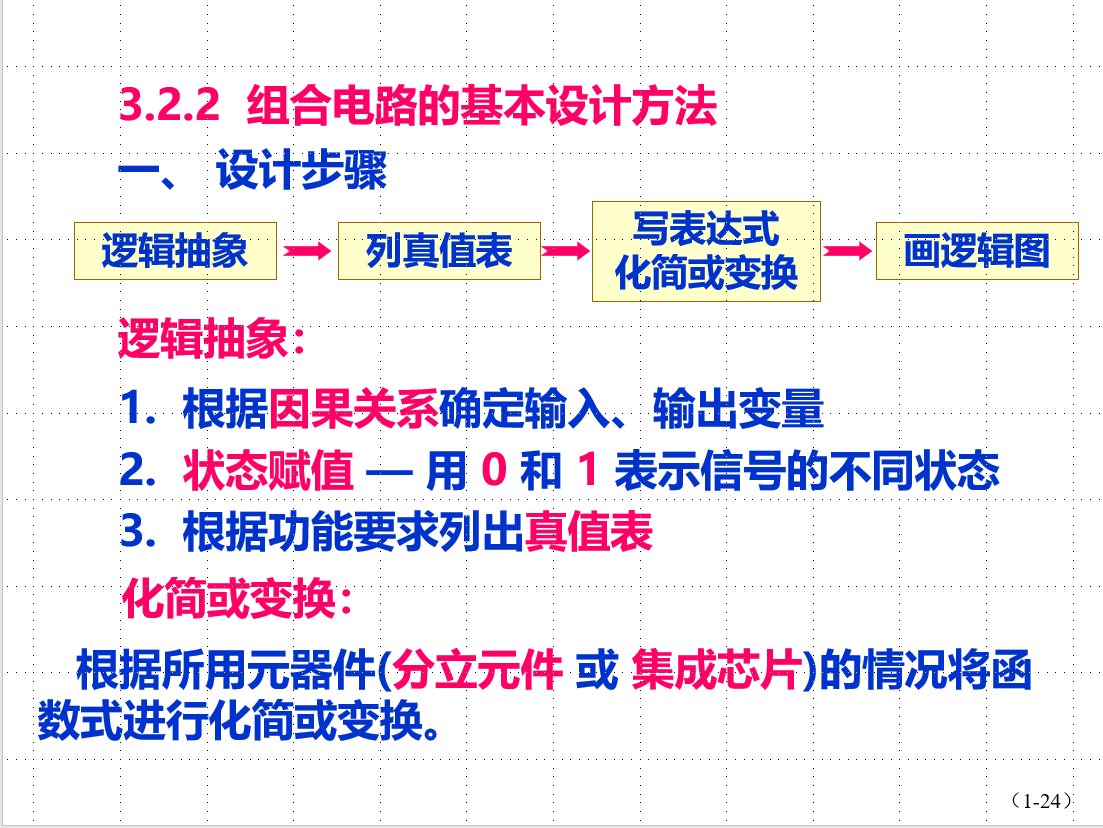
Attention:非的与非→或!!!
组合电路例题分析:
例1:
在F1中,可以将 A 视为 A非的非,根据非的与非为或,得到下图;
例2:
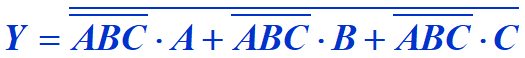
先利用结合律将A,B,C置于同一括号内,再加上非的非,可以化为:
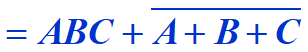 再利用反演运算,即:
再利用反演运算,即:
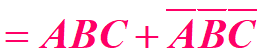 ;注意A+B+C上方的非要保留;
;注意A+B+C上方的非要保留;
例3:分析下图逻辑电路的功能:
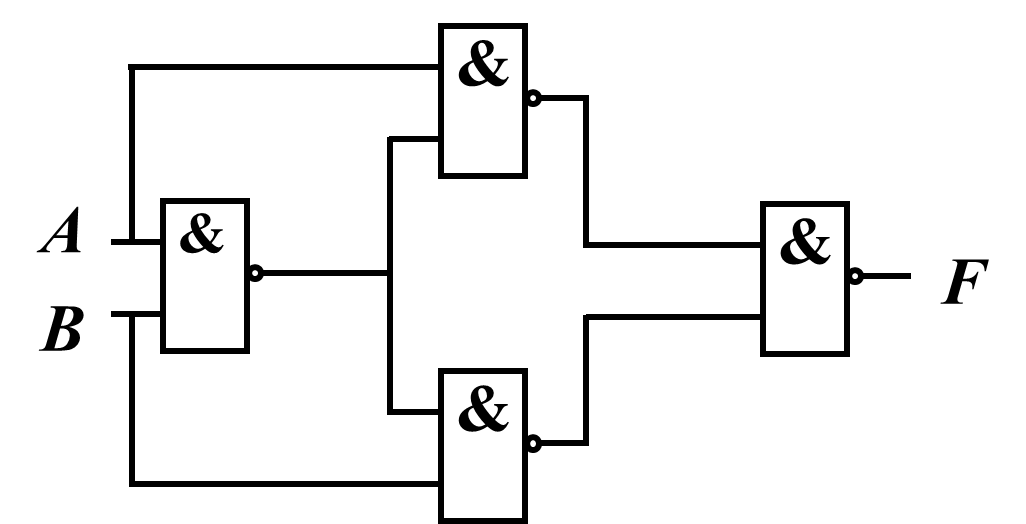
第一步,写出逻辑表达式:
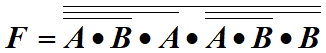 非的与非是或;
非的与非是或;
![]()
![]()
第二步,列出真值表:
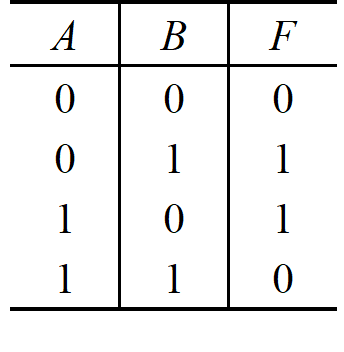
第三步,分析可知,此电路实现了异或功能;
例4:用与非门设计一个举重裁判表决电路。设举重比赛有3个裁判,一个主裁判和两个副裁判。杠铃完全举上的裁决由每一个裁判按一下自己面前的按钮来确定。只有当两个或两个以上裁判判明成功,并且其中有一个为主裁判时,表明成功的灯才亮
不妨设:设主裁判为变量A,副裁判分别为B和C;灯亮为1,灭为0;
第一步,穷举法列出真值表: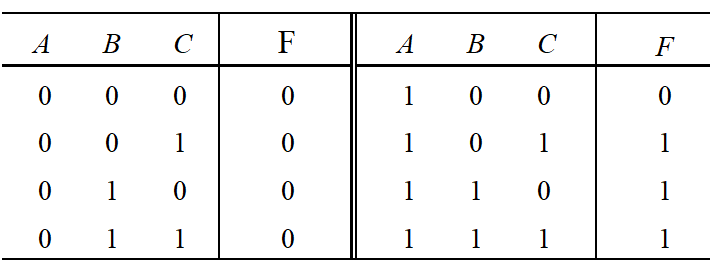
第二步,写出逻辑表达式并化为最简与或式: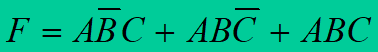
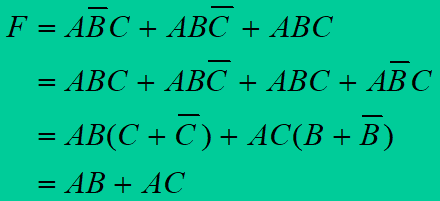
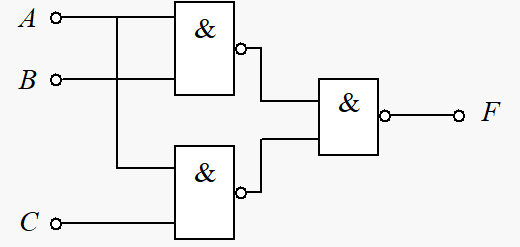
第三步,因题目要求与非门,所以进行逻辑变换:
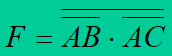
第四步,画出电路图:
编码器:
将多种信号状态转化为:2^n → n;用二进制表示不同的事物;
8 - 3 编码器;10 - 4 编码器 ;8 - 3 优先编码器;
n种输出状态,就有2^n种不同的输入信号状态;
译码器:
译码器是编码器的逆过程,即将n个二进制输入转化为2^n个输出信号;
2 - 4 译码器;3 - 8 译码器; 4 - 16 译码器;
3 - 8 二进制译码器(高电平有效):
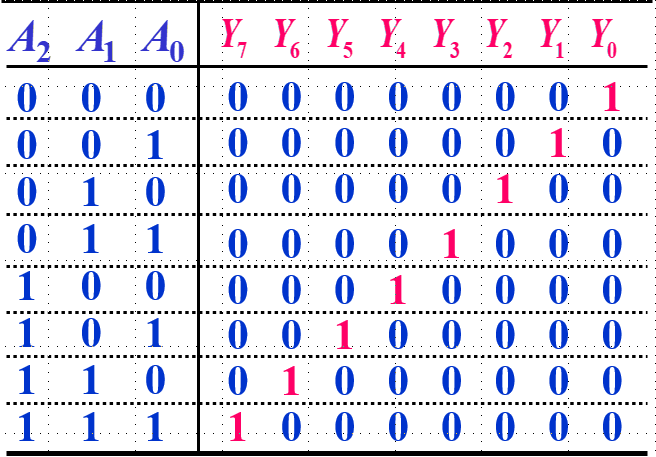
其逻辑表达式让我联系到了离散数学中真值表的极小项,取成真赋值;
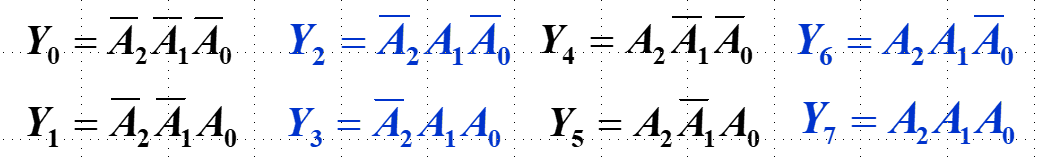
请对比 8 - 3编码器的真值表:
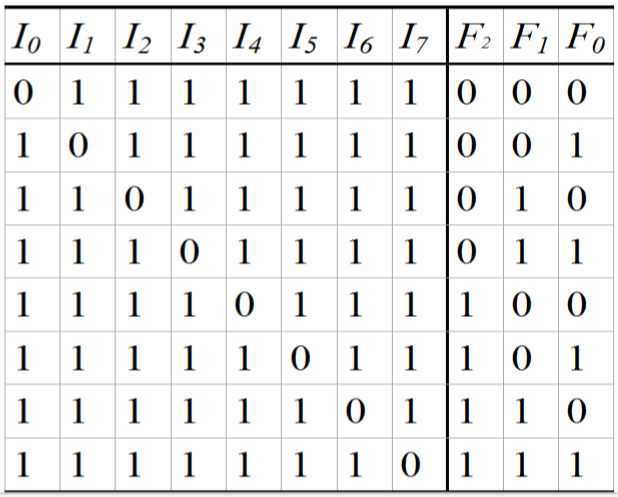
3 - 8 译码器逻辑图(输出低电平有效,即在输出端取非):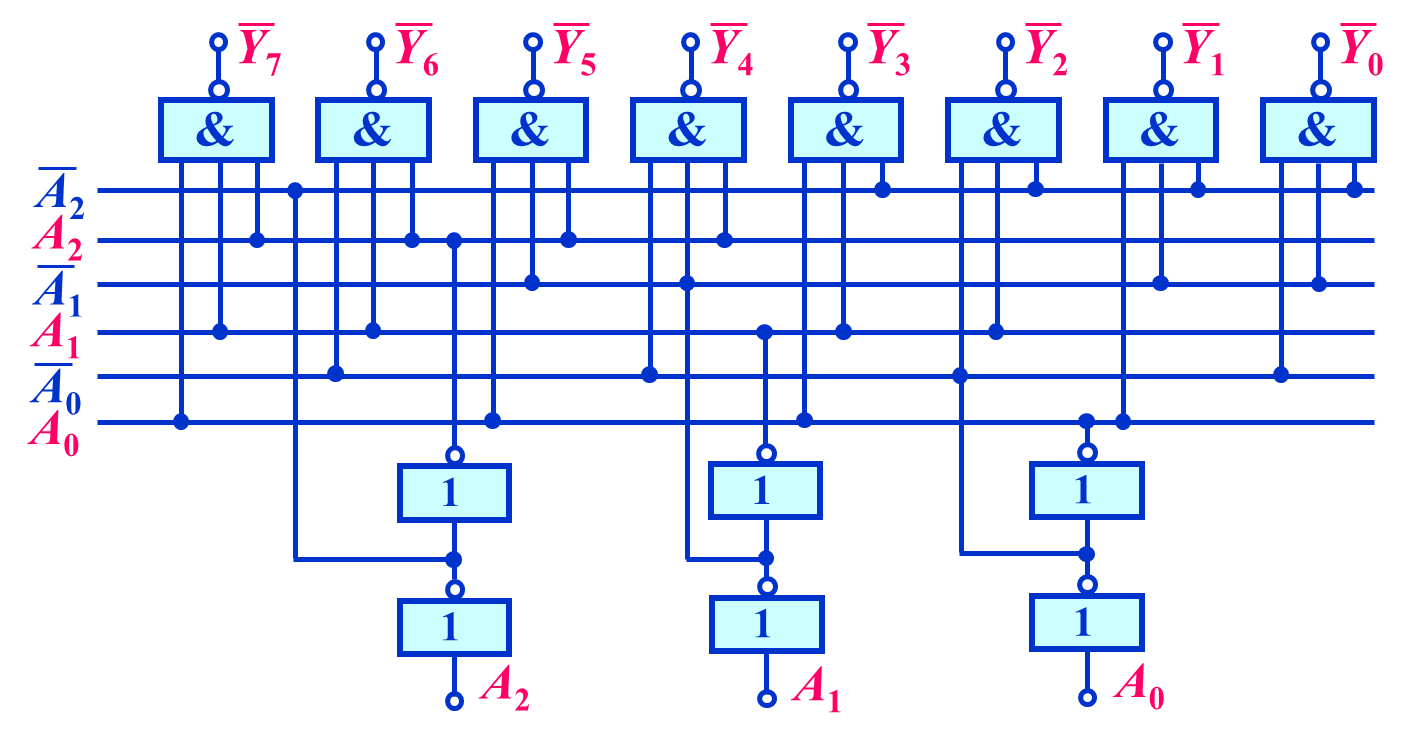
举例:当输入为 0 0 0时,输出为:1 1 1 1 1 1 1 0;
当输入为 1 1 1时,输出为:0 1 1 1 1 1 1 1;
使能端举例:
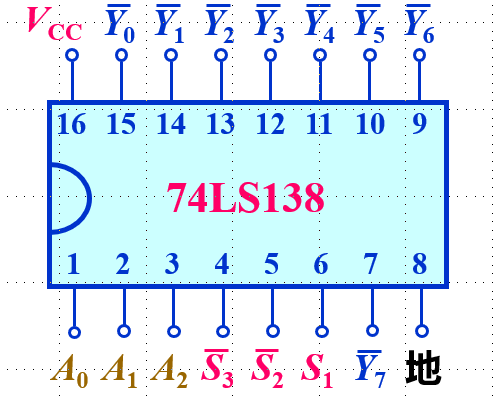
想要电路正常工作,则s3,s2接地,s1接电源;
数码显示器:2 - 10 进制译码器
共阳极:低电平驱动;输出为1:灭 输出为0: 亮
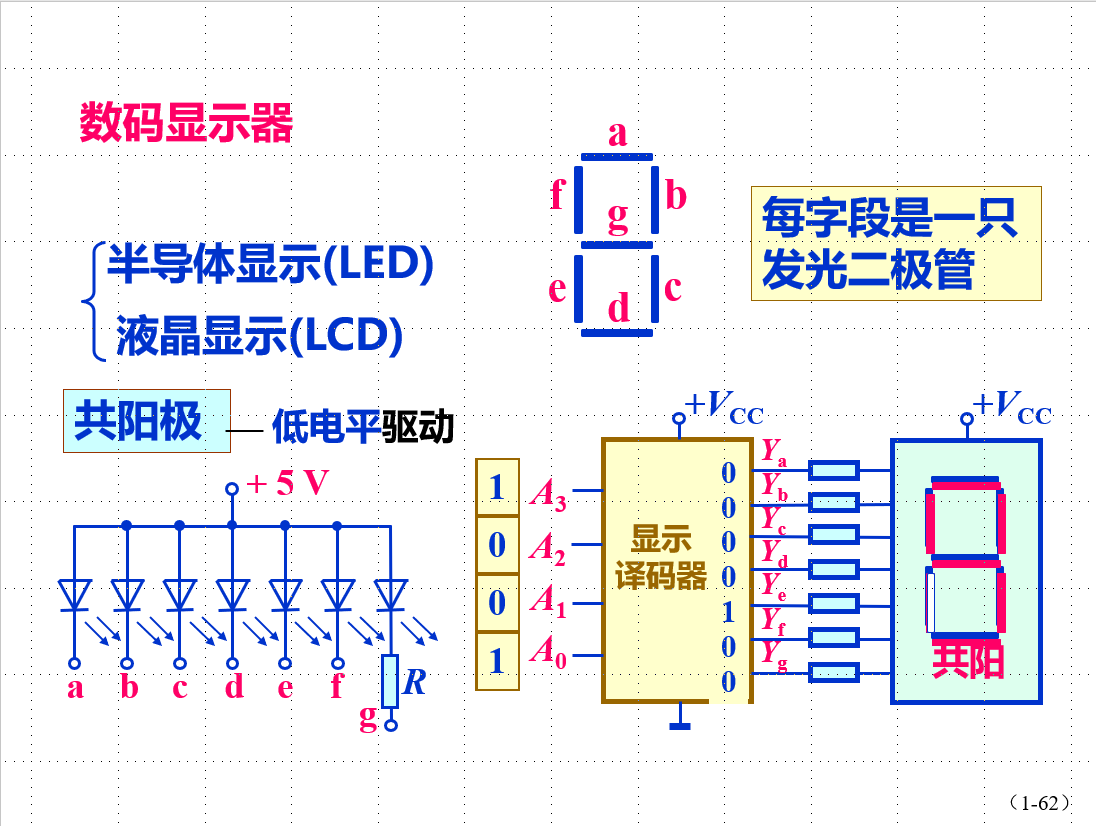
共阴极:高电平驱动;输出为0:灭 输出为1: 亮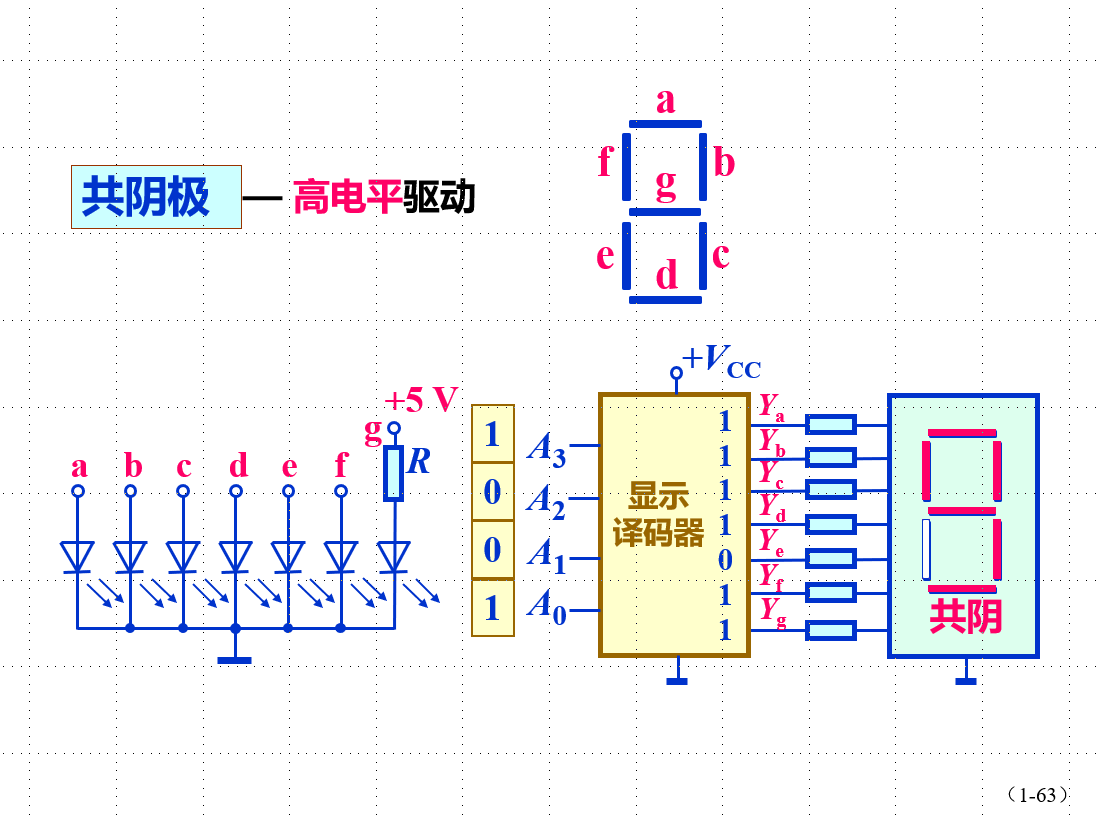
译码器的作用:其自身可以根据二进制数的不同来输出全部最小项;
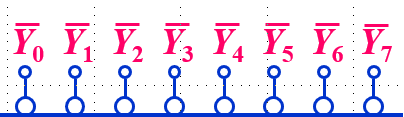
请注意,此时输出为极小项的非;
例题分析: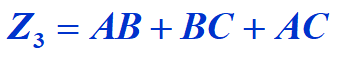
1.因为有3个变量,所以选择3 - 8译码器;
2.求出标准与非式:缺哪个,补哪个;AB→AB(C + C非);
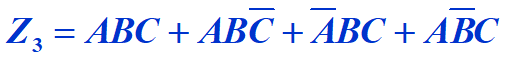
3.进行逻辑转换:![]()
![]()
4.m7→Y7 ;m6→Y6 ; m5→Y5 ;m3→Y3;即:四者非的与非;
5.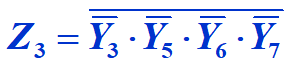
6.作图:
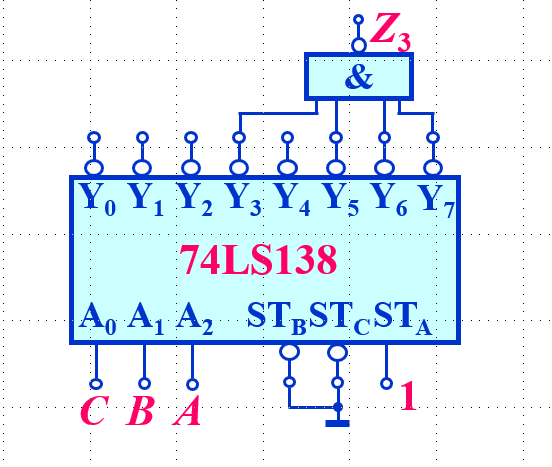
比较器:
(略)
加法器:
1.半加器(Half Adder):
两个 1 位二进制数相加不考虑低位进位。
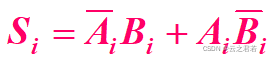
![]()
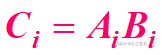
即:本位是A和B的异或,进位是A和B的与;
2.全加器(Full Adder):
两个 1 位二进制数相加,考虑低位进位。
真值表如下:
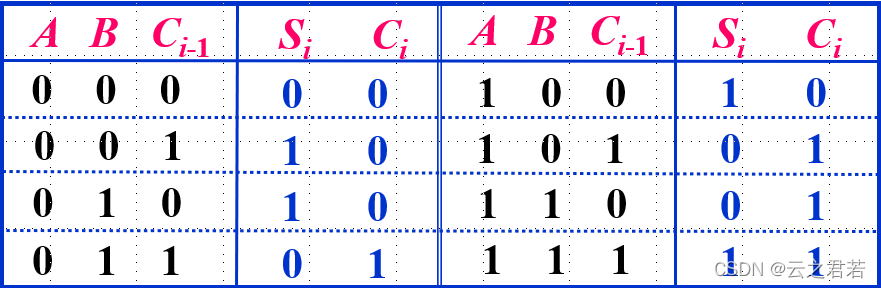
标准与或式如下:
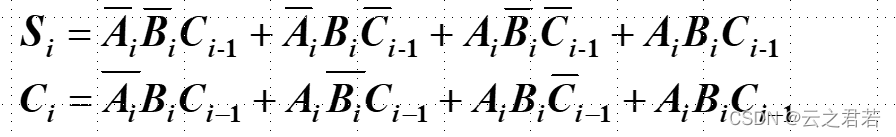
逻辑代换式如下: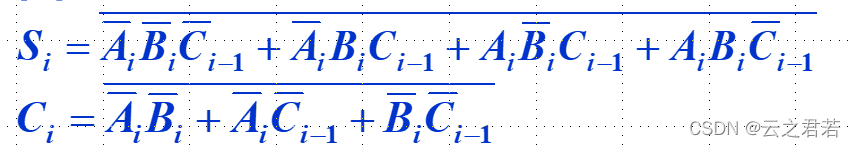
加法器的级联:
假定1个加法器的平均传输延迟时间为T;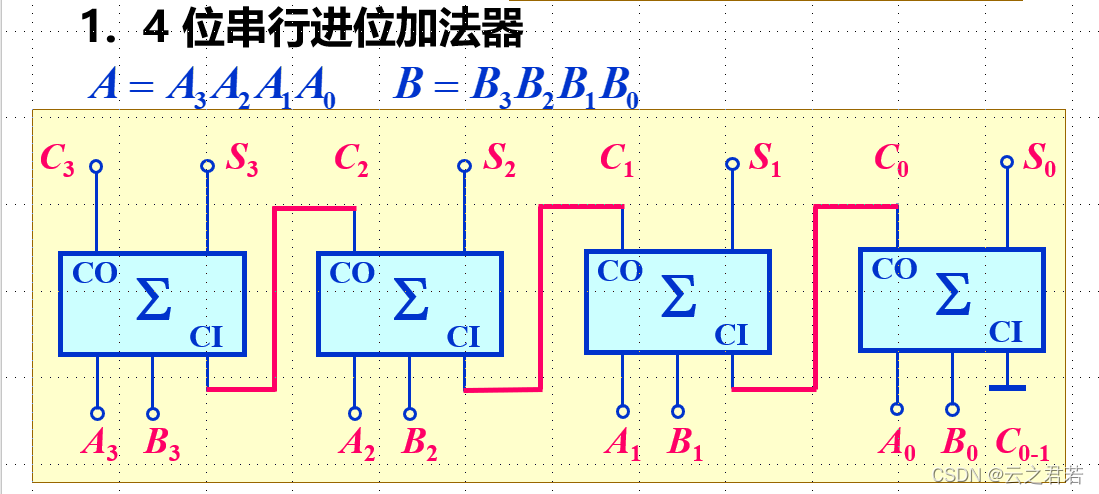
则,电路的总用时为4T; 注意,0位的C接地(不进位);
数据的传输方式:
并行传送和串行传送;
数据分配器:
定义:
广义上,其将一串行输入的数据,在n位分配地址的控制下,依次分配的2^n个通道上;
P.S.一个具有使能端的译码器可以作为一个数据分配器。
1路 - 4路 数据分配器:
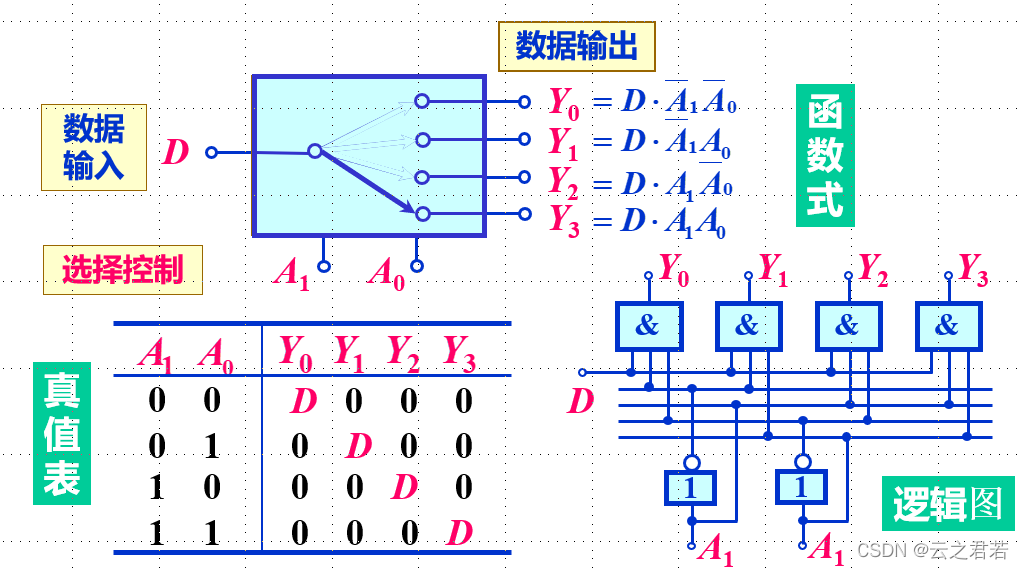
在2位地址(A1和A0)的控制,有选择地将数据D分配的Y0,Y1,Y2,Y3位;
n → 2 ^ n ;
Y0 = D * m0;Y1 = D * m1; Y2 = D * m2; Y3 = D * m3;
注意:逻辑图的5条平行线:从上到下依次为:D,A1非,A1,A0非,A0;
数据选择器:
数据选择器是数据分配器的逆过程;
定义:
其将2^n路并行输入的数据在n位地址的控制下,有选择地送到输出端的电路上;
4路 - 1路 数据选择器(省略逻辑图):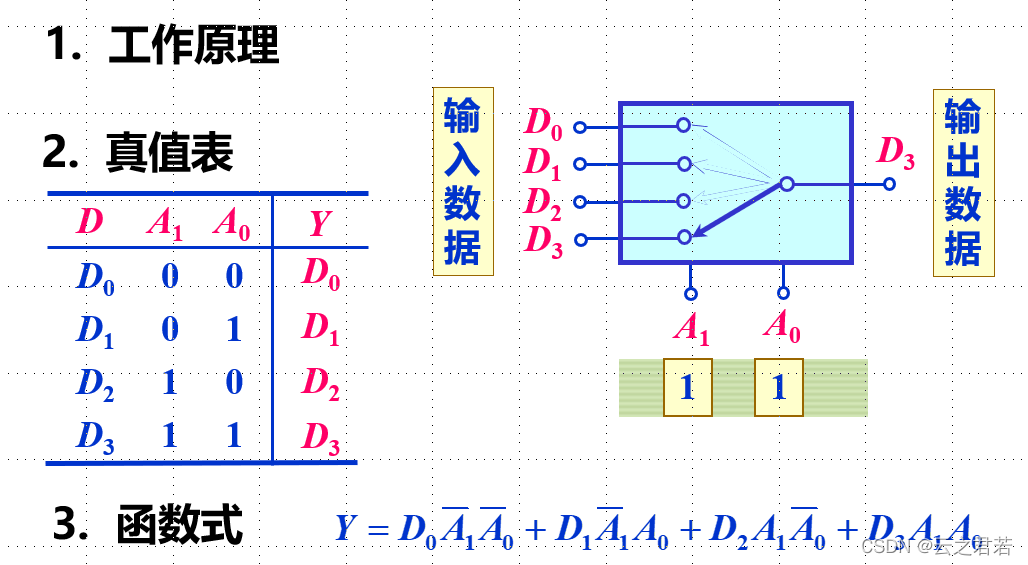
当m0时,输出D0;当m1时,输出D1;当m2时,输出D2;当m3时,输出D3;
2 ^ n → n ;
8 路 - 1路 数据选择器:
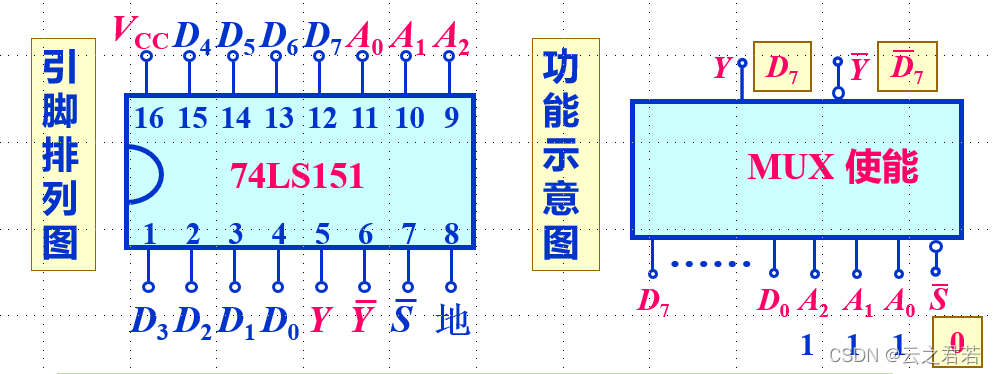
注意:D0 到 D7 是数据输入端; Y 和 Y非 是数据输出端;
而A0 A1 A2 是地址端;3 → 8 → 1; S非 是使能端,当且仅当值为0时使能;
数据选择器的拓展:
16路 - 1路: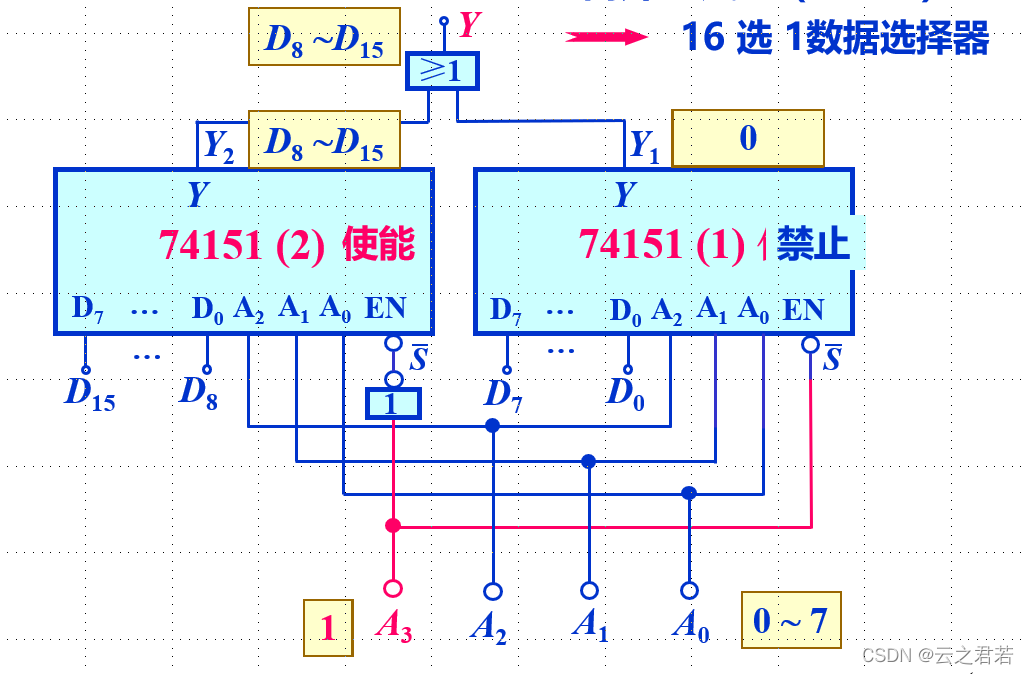
32路 - 1路:
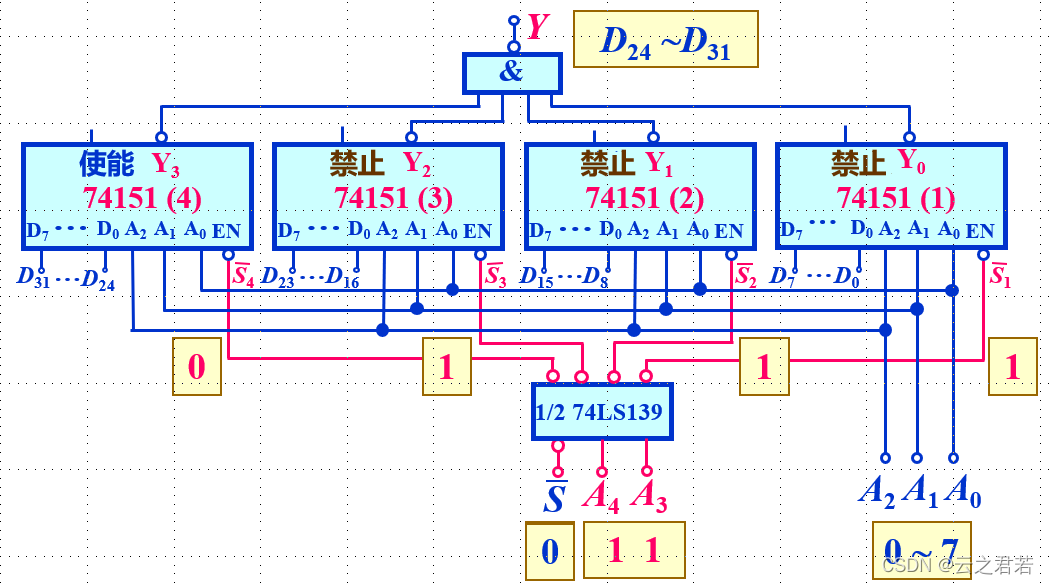
利用数据选择器实现组合逻辑函数:
因为任何组合逻辑函数都能以最小项的或的形式表示,而数据选择器的输出均为标准与或式,含地址的最小项,故可以使用数据选择器进行表达;
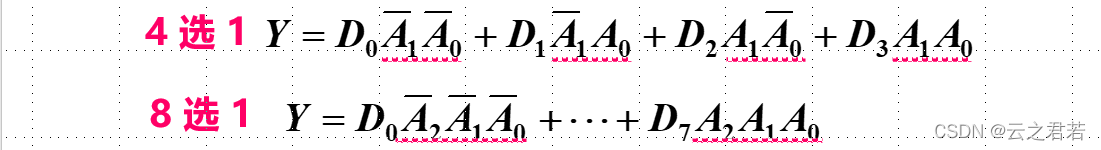
步骤1:有k个变量,则有k - 1个地址码;
步骤2:写出函数的标准与或式和选择器输出信号表达式;
步骤3:确定选择器各个输入变量的表达式;
步骤4:根据采用的数据选择器和求出的表达式画出连线图。
举例1:
因为有3个变量,所以选择2个地址码A0和A1;
函数的标准与或式:![]()
数据选择器表达式:![]()
不妨令:A0 = B ,A 1 = A;
则有:Y = D0A非B非 + D1A非B + D2AB非 + D3AB;
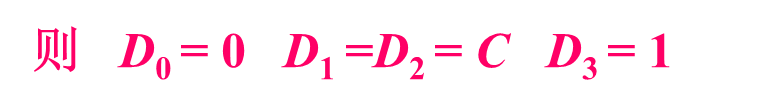
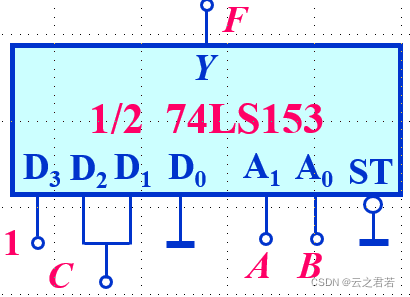
举例2:
奇偶校验器:
作用:检验数据在传输过程中是否出现差错,若出现则停止输出;
奇校验:加了校验位使得1的位数为奇数;
偶校验:加了校验位使得1的位数为偶数;
8位校验电路举例: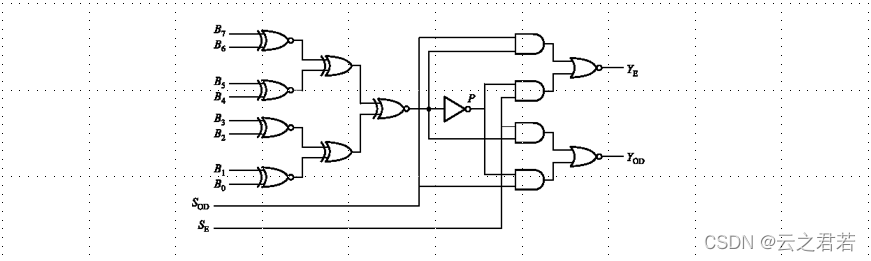
S(odd) = 1 ; S(even) = 0; 电路实行了奇校验 ;
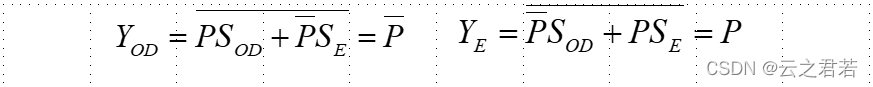
S(odd) = 0 ; S(even) = 1; 电路实行了偶校验 ;
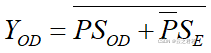
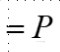
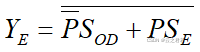
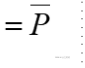
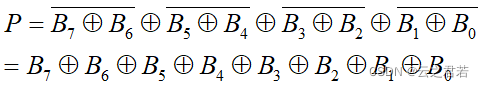
当8位中1的个数位奇数时,P = 1;当8位中1的个数位偶数时,P = 0;
图解原理分析: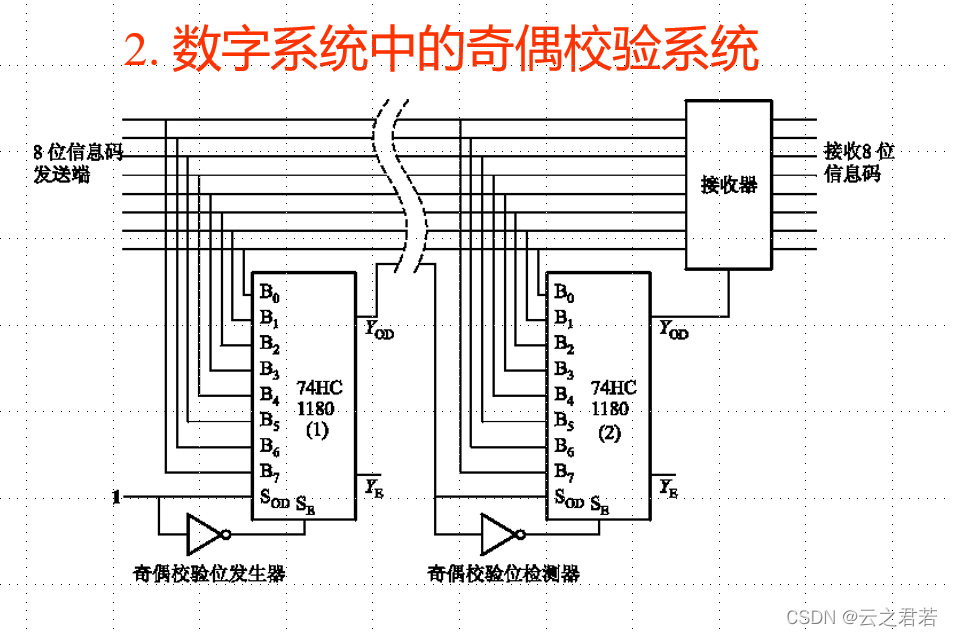
奇数:P = 1,奇校验:So = 1 ,Se = 0; 则:Yod = 0; Ye = 1;触发偶检验;
偶校验:S0 = 0 ,Se = 1; 则:Yod = 1; Ye = 0 ; (正确输出)
则:Yod = 1; Ye = 0 ; (正确输出)
偶数:P = 0,奇校验:So = 1 ,Se = 0; 则:Yod = 1; Ye = 0;触发奇检验;
奇校验:S0 = 1 ,Se = 0; 则:Yod = 1; Ye = 0 ; (正确输出)
则:Yod = 0; Ye = 1 ; (错误输出)
PLD:Programmable Logic Device(可编程逻辑器件)
概述:
1.按通用器件生产,但逻辑功能可由用户自己通过对器件编程来设定;
2.发展和分类(了解)
3.PLD内部电路的简化画法: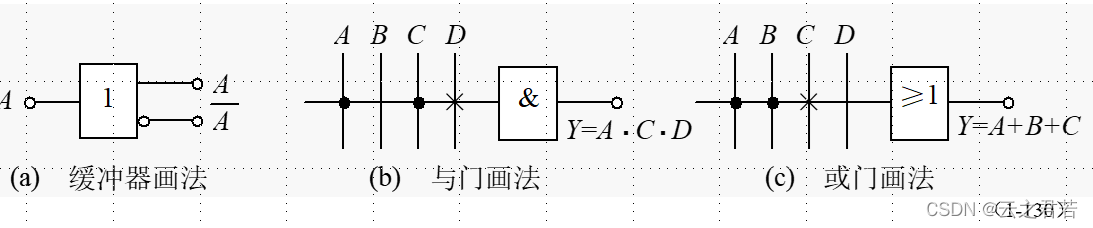
PLA及其应用:
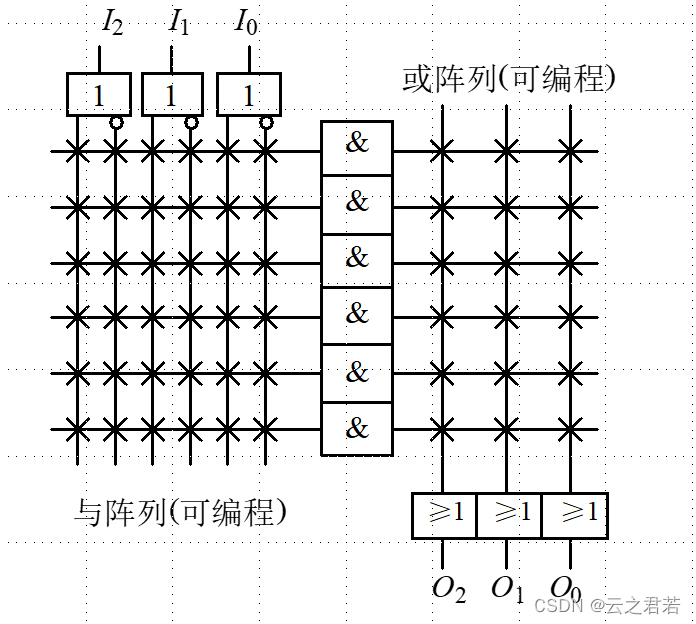
如何利用PLA实现逻辑电路?
首先化为最简与或表达式,尔后画出PLA的阵列图;
举个栗子:
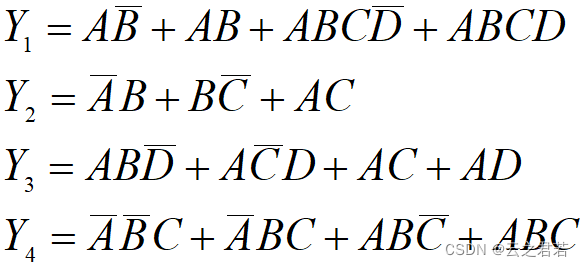
第一步:先将函数化为最简与或表达式;(可通过卡诺图化简)
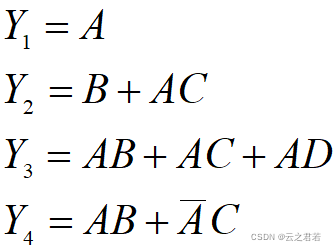
第二步:根据最简与或表达式作出阵列图(横为与,竖为或);
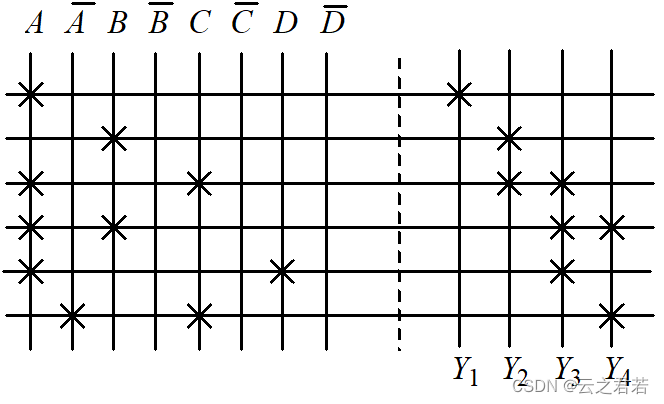
PAL及其应用:
举个栗子:竖线从左至右:A,A非,B,B非,C,C非,D,D非;
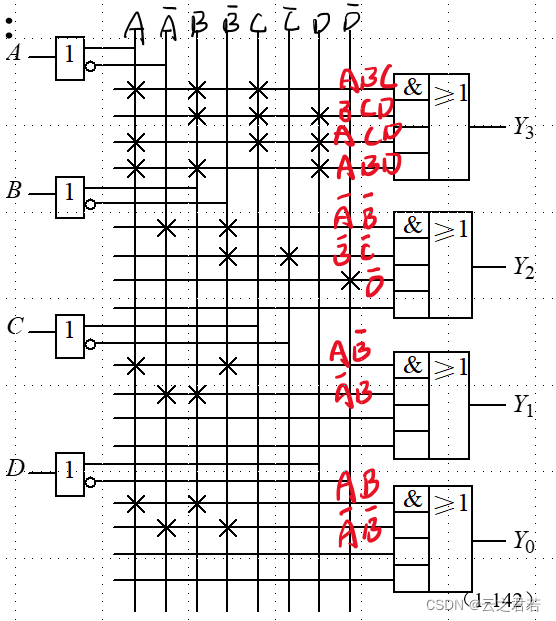
易知:
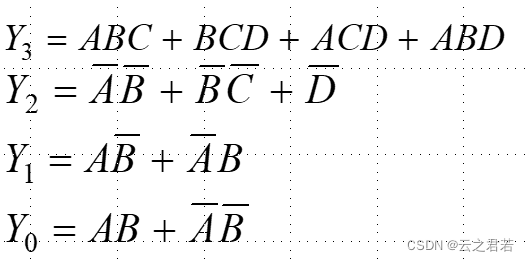
Chapter 4:集成触发电路和时序逻辑电路
概述
时序电路:任何时刻电路的输出,不仅和该时刻的输入信号有关,还取决于电路原来的状态。
时序电路的分类:
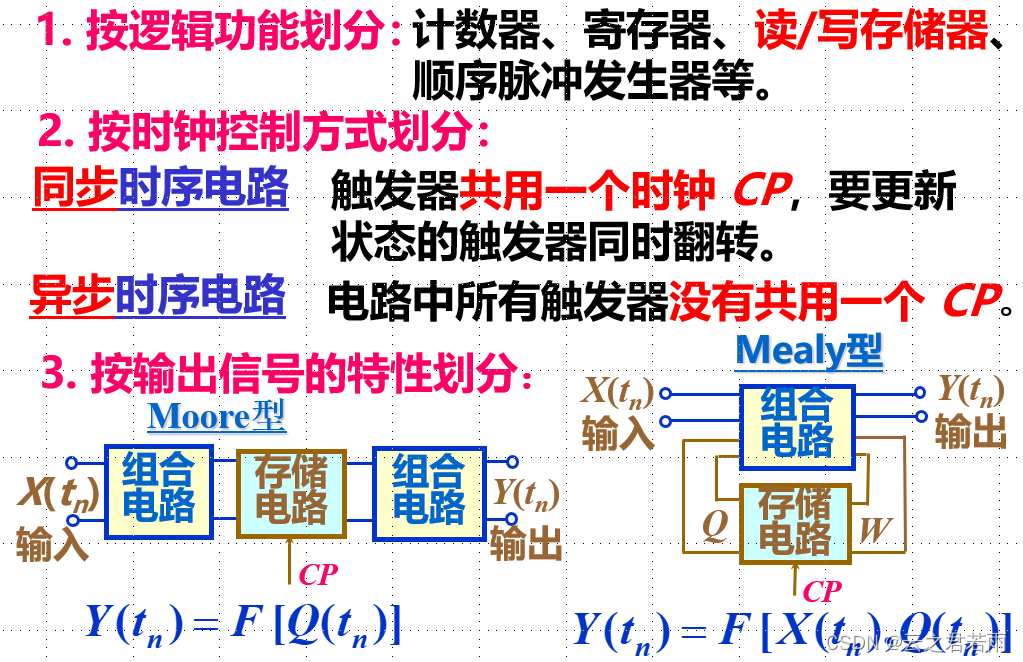
基本触发器:
基本触发器的分类:
基本R-S触发器、同步式触发器、边沿触发器、主从触发器......
基本触发器的原理:
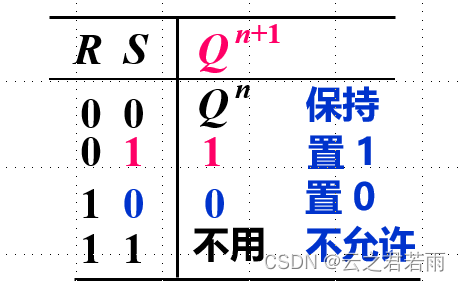
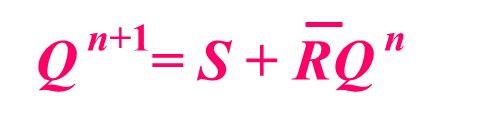
当R和S均为1时,Q和Q非均为1,不满足互补关系,所以说,Q的输出具有随机性(由两个门的传输延迟时间所决定)。因此,我们用“不允许”来表示;
波形图举例:
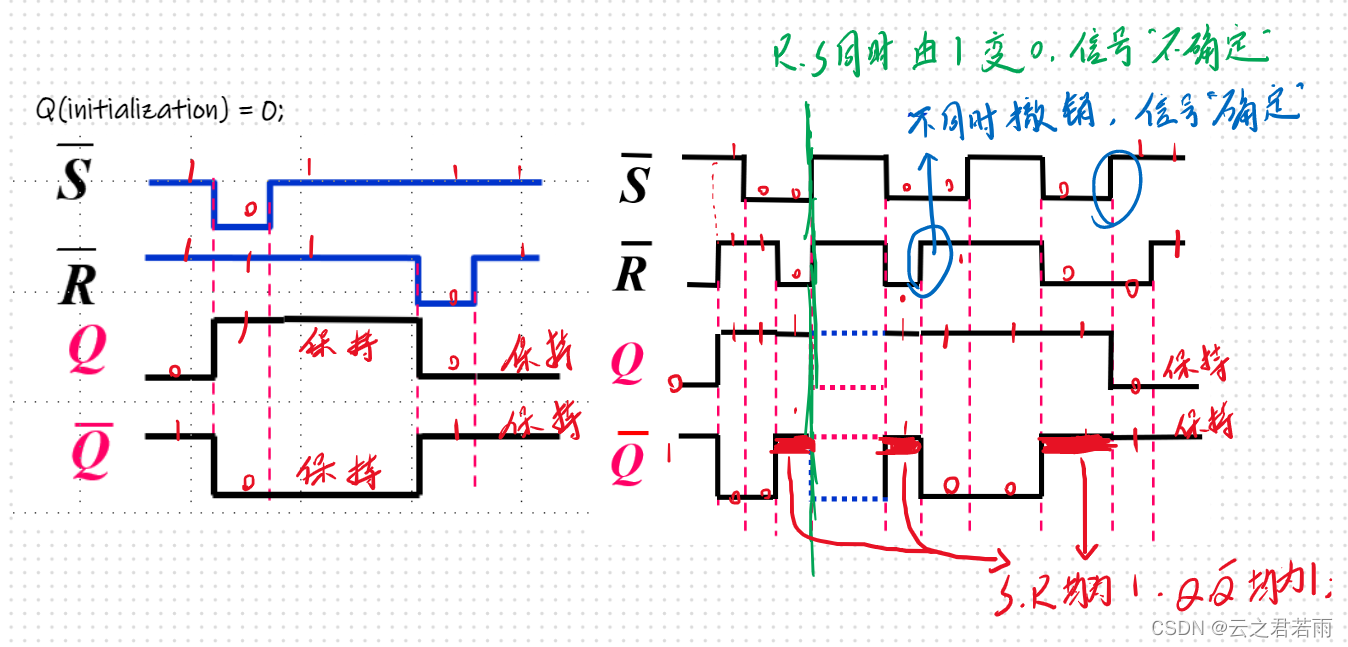
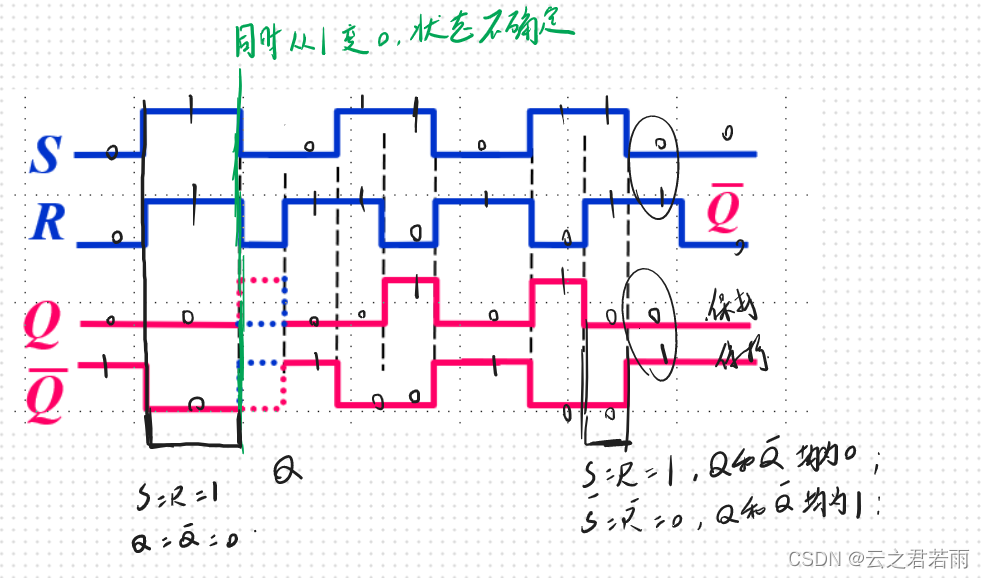
同步触发器:
——触发器的工作状态不仅受输入端 (R、S)控制,还受时钟脉冲(CP) 的控制。
同步触发器分为同步RS触发器和同步D触发器;
同步RS触发器:
电路图及其符号(高电平输入触发器):
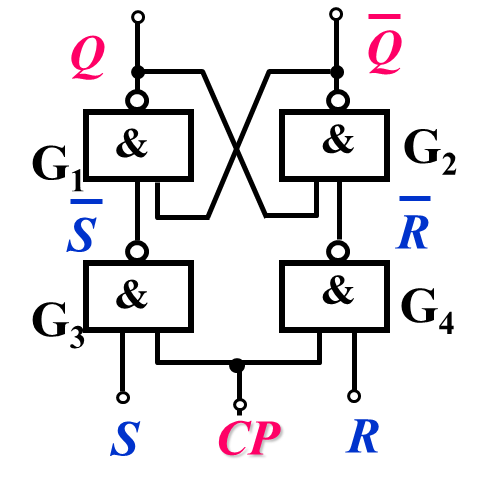

工作原理:

波形图:
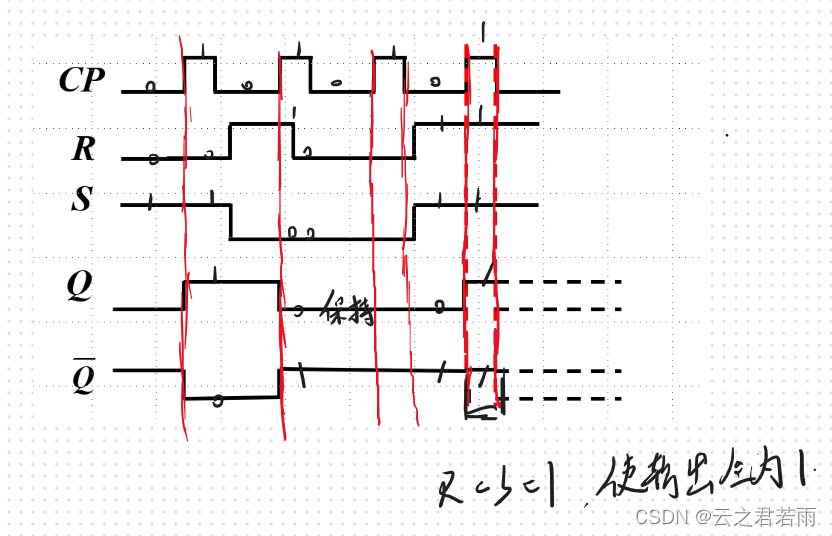
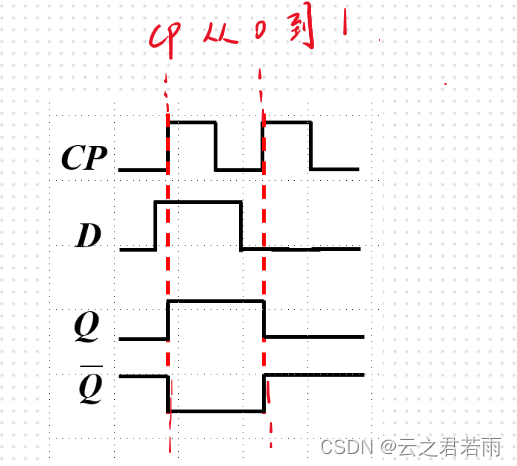
D触发器 :
CP=0时,A,B被阻塞,保持原态;
CP=1时,输出为D;
主从触发器:
主从RS触发器:
工作原理:
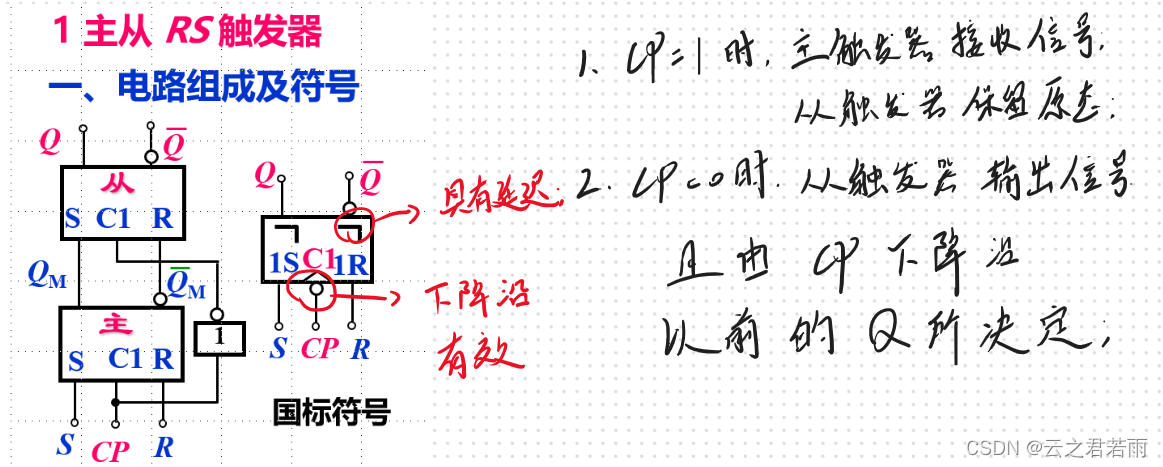
波形图:
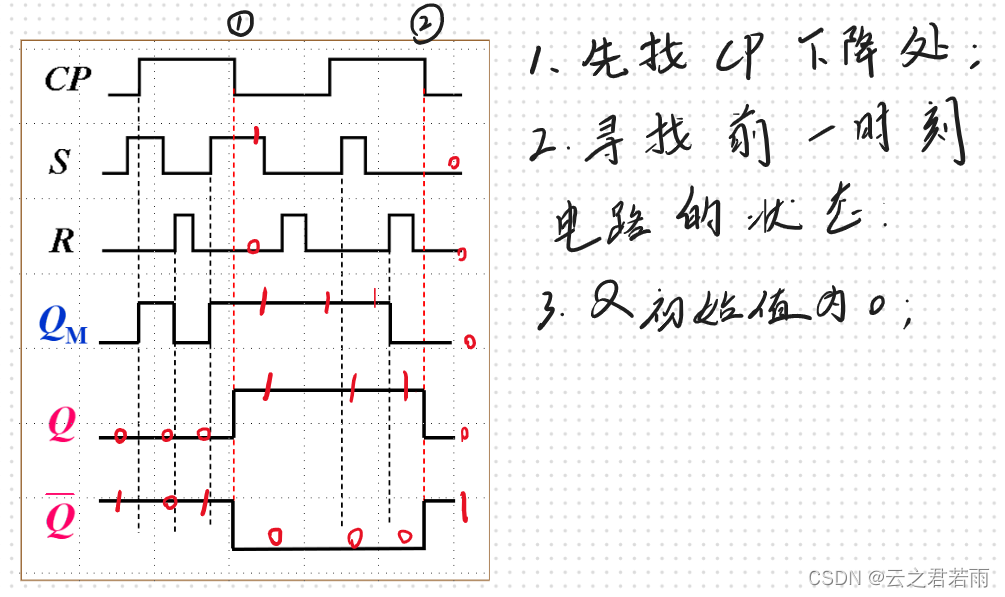
主从T'触发器:
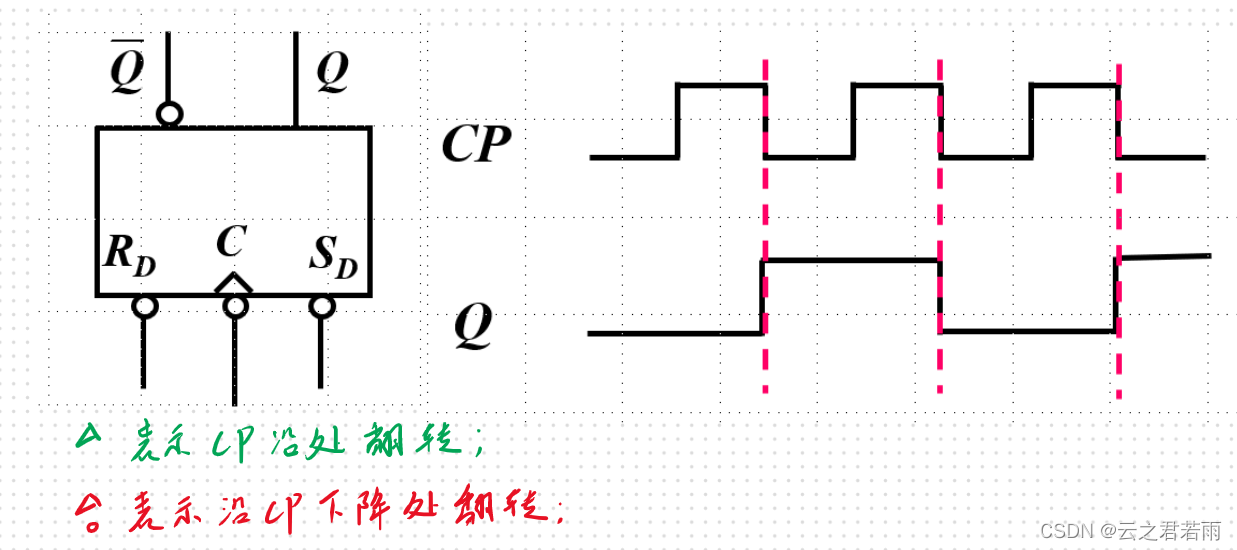 T触发器与T'触发器相比,仅加入了控制端T:当T=0时,CP不起作用;当T=1时,与T´相同。
T触发器与T'触发器相比,仅加入了控制端T:当T=0时,CP不起作用;当T=1时,与T´相同。
JK触发器(功能最完善的触发器):
特性方程: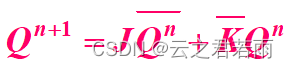
特性表:
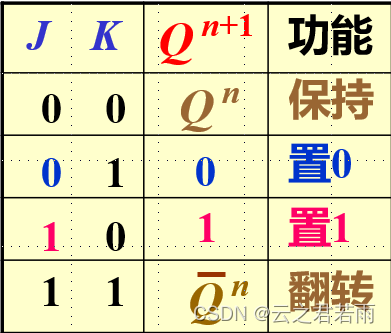
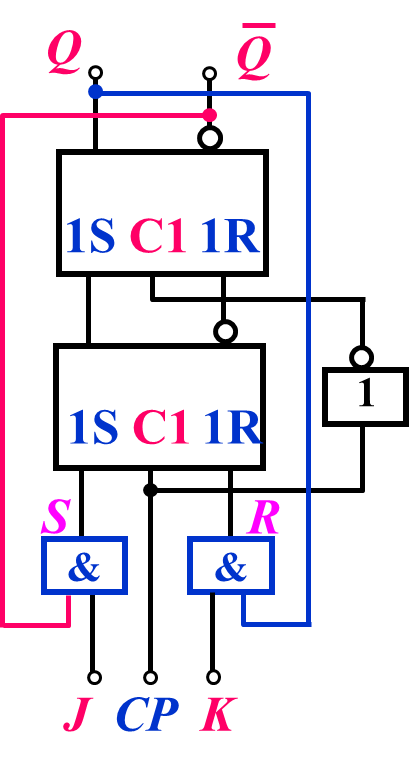
功能表及其逻辑符号:
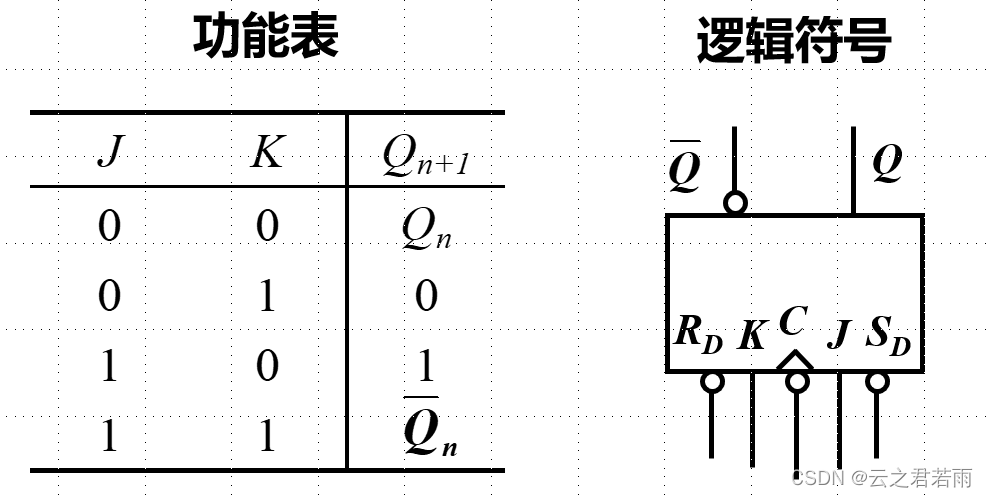
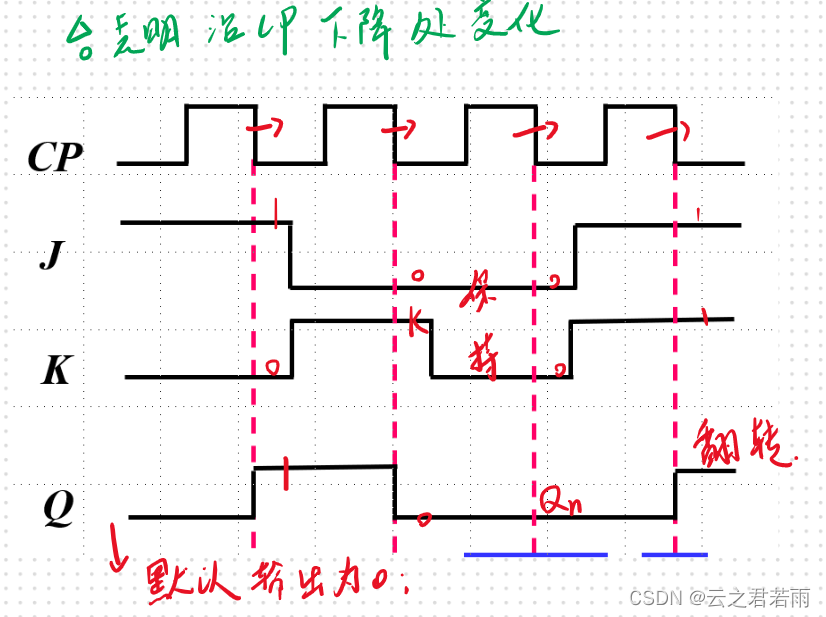
时许图:
 ----------------------------------------------未完待续,持续更新--------------------------------------------------------
----------------------------------------------未完待续,持续更新--------------------------------------------------------
参考资料:
1.郑家龙,王小海,章安元.《集成电子技术基础教程》北京:高等教育出版社;
2.杨玉叶电子技术课件(PPT);
最后
以上就是简单镜子最近收集整理的关于《数字电路分析》学习札记前言 :Chapter 1:数字逻辑基础 Chapter2:集成逻辑门电路;Chapter 3:组合逻辑电路 Chapter 4:集成触发电路和时序逻辑电路参考资料:的全部内容,更多相关《数字电路分析》学习札记前言内容请搜索靠谱客的其他文章。
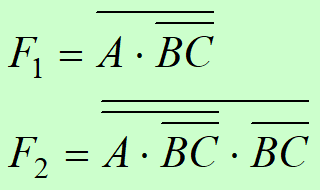
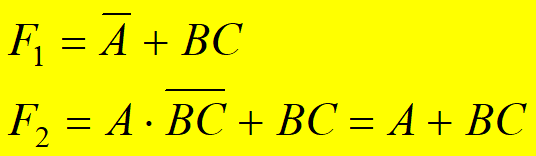








发表评论 取消回复