计算机组成原理（第二章）

第二章思维导图如下：

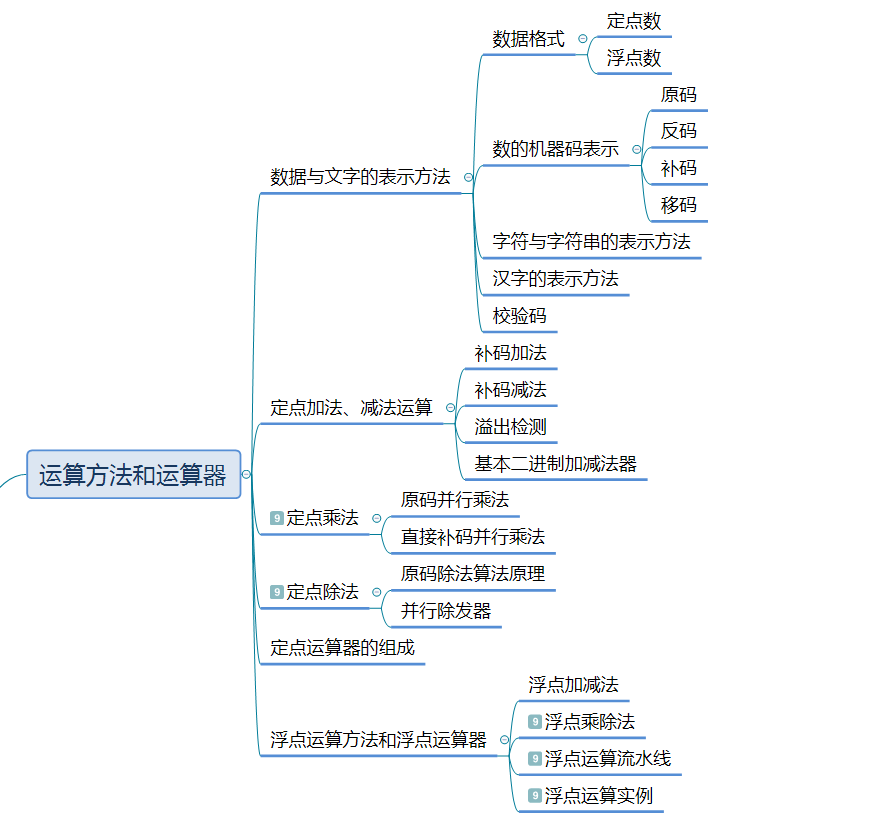
0. 数据类型

1. 按数制分：二值进制、十进制、八进制、十六进制。
2. 按数据格式分： 真值、机器数。
3. 按数据的表示范围分：定点数、浮点数。
4. 按能否标识负数分：无符号数、有符号数。

1. 数据与文字的表示方法

1.1 数据格式

定点数

1. 定点数：小数点固定在某一位置的数据。
   • 纯小数：$x_0.x_{-1}{x}_{-2}{x}_{-3}\dots \dots x_{-n}$
     • 表示形式：$x_s$ 为符号位 ；$x_0$为0。
       有符号数：$x=x_s{x}_{-1}{x}_{-1}\dots \dots x_{-n}$ $|x|\le 1-2^{-n}$
       无符号数：$x=x_0{x}_{-1}{x}_{-1}\dots \dots x_{-n}$ $0\le |x|\le 1-2^{-n}$
   • 纯整数：$x_n{x}_{n-1}{x}_{n-2}\dots \dots x_1{x}_0$
     • 表示形式：$x_s$ 为符号位 ；$x_n$为数值位。
       有符号数：$x=x_sx_{n-1}……x_{1}x_{0} $ $|x|\le 1-2^{-n}$
       无符号数：$x=x_n{x}_{n-1}\dots \dots x_1{x}_0$ $0\le |x|\le 1-2^{-n}$
2. 定点机的特点：
   • 所能表示的数据范围小；
   • 数据精度较低；
   • 存储单元利用率低。

浮点数

1. 浮点数：小数点位置可变，形如科学计数法中的数据表示。

2. 格式定义：

   • M：尾数，是一个纯小数，表示数据的全部有效数位，其位数决定数值的精度；
   • R：基数，可以取2、8、10、16，表示当前的数制；
   • e：阶码，是一个整数，用于指出小数点在该书中的位置，其位数决定数据的取值范围；

3. 机器数的一般表示形式：

   阶符	阶码	数符	尾数
   数符	阶符	阶码	尾数

4. 规格化表示：

   • 要求：|尾数| $\ge$ 0.5，（ 是否为规格化浮点数与阶码无关 ）；
     • 尾数原码表示：最高数值位为1；
     • 尾数补码表示：最高数值位与符号位相反；
   • 处理：
     • 左规处理（数值向左移动）；
     • 右规处理（数值向右移动）；

5. 最值：

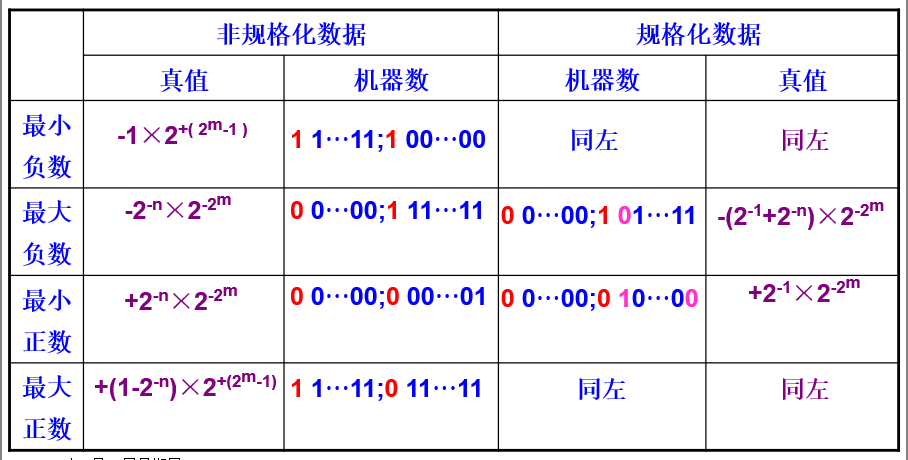
6. 32位浮点数的IEEE754标准表示：
   | 数符S | 阶码E | 尾数M |

   • 数符S：1位，表示浮点数的符号；
   • 尾数M：23位，原码纯小数表示，小数点在尾数域的最前面；
   • 阶码E：8位，采用有偏移值的移码表示（移127码）；
   • 真值：$N=(-1{)}^S\ast (1.M)\ast 2^{E-127}$

7. 	S	E	M
   正零	0	0000 0000	000……000
   负零	1	0000 0000	000……000
   正无穷	0	1111 1111	000……000
   负无穷	1	1111 1111	000……000

1.2 数的机器码表示

原码

1. 定义：
   • 定点小数：
     $$[x{]}_{原}\{\begin{array}{ll}x,& \text{1>x≥0}\\ 1-x=1+|x|,& \text{0≥ x>-1}\end{array}$$
   • 定点整数：
     $$[x{]}_{原}\{\begin{array}{ll}x,& \text{2n>x≥0}\\ 1-x=1+|x|,& \text{0≥ x>−2n}\end{array}$$
2. 特点:
   • 0的有两种表示法；$[+0{]}_{原}=0000；[-0{]}_{原}=1000$
   • 数据表示范围：
     • 定点小数：$-1<x<1$
     • 定点整数：$-2^n<x<2^n$
   • 符号位与数值位不能一起参与运算

补码

1. 定义：

   • 定点小数：
     $$[x{]}_{补}\{\begin{array}{ll}x,& \text{1>x≥0}\\ 2+x=2-|x|,& \text{0≥ x≥-1}\end{array}(mod2)$$
   • 定点整数：
     $$[x{]}_{补}\{\begin{array}{ll}x,& \text{2n>x≥0}\\ 2^{n+1}+x=2^{n+1}-|x|,& \text{0≥ x ≥-2n}\end{array}(mod{2}^{n+1})$$

2. 特点：

   • 0的编码唯一：0000
   • 数据表示范围：
     • 定点小数：$-1<x<1$
     • 定点整数：$-2^n\le x<2^n$
   • 只要结果不溢出，符号位可与数值位一起参与运算
   • $[[x{]}_{补}{]}_{补}=[x{]}_{原}$

3. 有原码求补码

   • 除符号位以外，其余各位按位取反，末位加一；
   • 除符号位以外，从最低位开始，遇到的第一个1以前各位保持不变，之后各位取反。

4. 求相反数的补码：由$[x{]}_{补}$求$[-x{]}_{补}$ （连同符号位的所有位一起取反，末位加一）。

移码

1. 定义：
   $$[x{]}_{移}=2^n+x{2}^n>x\ge -2^n$$
2. 特点：
   • 0的表示方法唯一：1000；
   • 与补码符号位相反，数值位相同；
   • 最高位为0表示负数，为1表示整数；
   • 可以较为直观的判断两个数据的大小（全为0时所对应真值最小，全为1时所对应真值最大）；
   • 表示浮点数阶码时，容易判断是否下溢。

1.3 字符与字符串的表示方法

1. ASCII码：8位，可表示128个字符，最高位为0，最高位可进行奇偶校验。
2. 字符串：连续的一串字符，每个字节存一个字符。

1.4 校验码

1. 数据校验的基本原理是扩大码距。
2. 码距：任意两个合法码之间不同的二进制位的最少位数。

奇偶校验码

1. 原理：在数据中增加1位奇偶校验位，是码距有1增到2。
2. 类型：
   • 偶校验：每个码字(包括校验位)中1的数目为偶数；
   • 奇校验：每个码字(包括校验位)中1的数目为奇数。
3. 过程：
   • 发送端：按照校验类型，在发送数据后添加校验位P；
   • 接收端：对接收到的数据（包括校验位）进行同样类型的校验，决定数据传输中是否存在错误。
4. 特点：具有检错能力（只能检测有奇数个错误的情况），但无纠错能力。

海明校验码

1. 原理：在一个数据中加入几个校验位，每个校验位和某几个特定的信息位构成偶校验的关系；接收端对每个偶关系进行校验，产生校验因子；通过校验因子区分无错和码字中的n个不同位置的错误；
2. 过程：

   • 确定校验位的位数：

     • 设K为有效信息的位数，r为校验位的位数，则整个码字的位数N应满足不等式：
       $$N=K+r\le 2^r-1,(N,K)为海明码$$

   • 确定校验位的位置：

     • 每个校验位$P_i$从低到高被分在海明码中位号$2^{i-1}$的位置。

   • 校验分组：

     • 海明码的每一位Hi有多个校验位校验，其关系是被校验的每一位位号等于校验它的各校验位的位号之和；
     • 每个信息位的位置写成用2的幂次之和的形式 ；
       例如下图：
       

   • 校验位的形成：

     • $P_i$ ＝第i组中所有位(除$P_i$)求异或;
     • 为了能检测两个错误，增加一位校验$P_{j＋1}$，放在最高位;
     • $P_{i+1}$ ＝所有位(包括P)求异或。

   • 接收端校验：

     • 接收端接收到数据后，分别求$S_1，S_2，S_3，\dots ，S_i$ ：
       $S_i$＝第j组中所有位(包括$P_i$)求异或
       $S_{i+1}＝P_{i+1}$ ⊕所有位(包括$P_1，P_2，\dots ，P_i$)求异或；
       当$S_{i+1}＝1$时，有一位出错；
       由$S_i,\dots \dots S_3{S}_2{S}_1$的编码指出出错位号，将其取反，即可纠错。
       当$S_{i+1}＝0$时，无错或有偶数个错（两个错的可能性比较大）；
       当$S_i,\dots \dots S_3{S}_2{S}_1=0\dots \dots 000$时，接收的数无错，否则有两个错。
3. 特点：既能检错，又能纠错。

2. 定点加法、减法运算

2.1 补码加法

1. 定点整数： $[x+y{]}_{补}=[x{]}_{补}+[y{]}_{补}(mod{2}^{n+1})$
2. 定点小数： $[x+y{]}_{补}=[x{]}_{补}+[y{]}_{补}(mod2)$

2.2 补码减法

1. 定点整数： $[x-y{]}_{补}=[x{]}_{补}+[-y{]}_{补}(mod{2}^{n+1})$
2. 定点小数： $[x-y{]}_{补}=[x{]}_{补}+[-y{]}_{补}(mod2)$

2.3 溢出概念与检测方法

1. 溢出：在定点数机器中，数的大小超出了定点数能表示的范围。
   • 上溢：数据大于机器所能表示的最大正数；
   • 下溢：数据小于机器所能表示的最小负数。
2. 判别方法：

   • 直接判别法：

     • 同号补码相加，结果符号位与加数相反；
     • 异号补码相减，结果符号位与减数相同。

   • 变形补码判别法：采用双符号位表示补码。

     符号位	结果
     00	正
     01	上溢
     10	下溢
     11	负

   • 进位判别法：最高数值位的进位与符号位的进位是否相同。

3. 定点乘法运算

3.1 串行乘法

1. 乘法运算 ＝ 加法＋移位。
   若乘数数值位n = 4，则累加 4 次，移位4 次。
2. 乘法过程
   • 由乘数的末位决定被乘数是否与原部分积相加；
   • 被乘数只与部分积的高位相加；
   • 部分积右移一位形成新的部分积；
   • 同时乘数右移一位（末位移丢）；
   • 空出高位存放部分积的低位。
3. 硬件构成
   3个具有移位功能的寄存器、一个全加器。

原码乘法（符号位与数值位分开计算）

1. 原码一位乘
   数值位运算规则：

   • 被乘数和乘数均取绝对值参加运算，符号位单独考虑；
   • 被乘数取双符号位，部分积的长度同被乘数，初值为0；
   • 从乘数的最低位Yn开始判断：
   • 若Yn＝1，则部分积加上被乘数|X|，然后右移一位；
   • 若Yn＝0，则部分积加上0，然后右移一位。
   • 重复，判断n次。

2. 原码两位乘
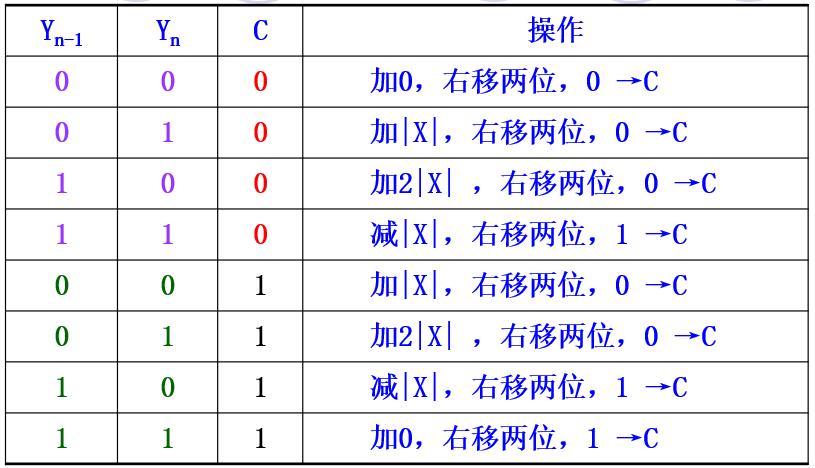
   数值位运算规则：

   • 部分积和被乘数均采用三位符号位；
   • 乘数末位增加1位C，其初值为0，运算过程见表；

   乘数字长与运算步骤：

   • 若乘数字长为偶数（不含符号），最多做n/2+1次加法，需做n/2次移位，最后一步不移位；
   • 若尾数字长n为奇数（不含符号），增加一位符号0，最多做n/2+1次加法，需做n/2+1次移位，最后一步右移一位。
     

最后

以上就是刻苦柠檬为你收集整理的计算机组成原理知识点-第二章计算机组成原理（第二章）0. 数据类型1. 数据与文字的表示方法2. 定点加法、减法运算3. 定点乘法运算的全部内容，希望文章能够帮你解决计算机组成原理知识点-第二章计算机组成原理（第二章）0. 数据类型1. 数据与文字的表示方法2. 定点加法、减法运算3. 定点乘法运算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。