撤销与重做 | 模型实现
文章目录
- 撤销与重做 | 模型实现
- 一. 撤销与重做
- 二. 撤销与重做功能的需求描述
- 1. 撤销 Undo
- 2. 重做 Redo
- 3. 综合情况
- 三. 双栈法实现
- 四. 链表法实现
- 五. 结束语
- 六. 提示
一. 撤销与重做
撤销(Undo)与重做(Redo)操作在日常工作中的使用,想必大家是非常熟悉的。撤销与重做给用户带来更高的容错率,其重要程度可以说仅亚于复制粘贴。也正是因为撤销与重做操作的实用性与重要性,当我进行一个软件项目的开发时,也希望给用户实现这两项操作。
那么在开发者的角度,如何为用户实现撤销与重做的功能呢。经过我自己的思考,本文提供两个模型思路,来实现撤销与重做操作。
二. 撤销与重做功能的需求描述
1. 撤销 Undo
撤销操作需要完成的是:在用户对被操作对象完成有限次操作后。用户的操作使对象到达某状态。此时再执行撤销操作,使得用户可以进行有限次的撤销操作后回到先前被操作对象的所有状态。
上述描述是一个非常抽象的概念。我们接下来进行详细解释。
设用户对被操作对象 O b j Obj Obj,执行了 n n n 次操作为 o i , ( i = 1 , 2 , 3 , . . . , n ) o_i,(i=1,2,3,...,n) oi,(i=1,2,3,...,n)。每次操作前,被操作对象处于状态 s i , ( i = 0 , 1 , 2 , 3 , . . . , n ) s_i,(i=0,1,2,3,...,n) si,(i=0,1,2,3,...,n),其中 s 0 s_0 s0 为初始状态,即一开始用户尚未做任何操作时备操作对象的状态。基于上述描述我们可以得到以下图示,表示用户操作的过程。
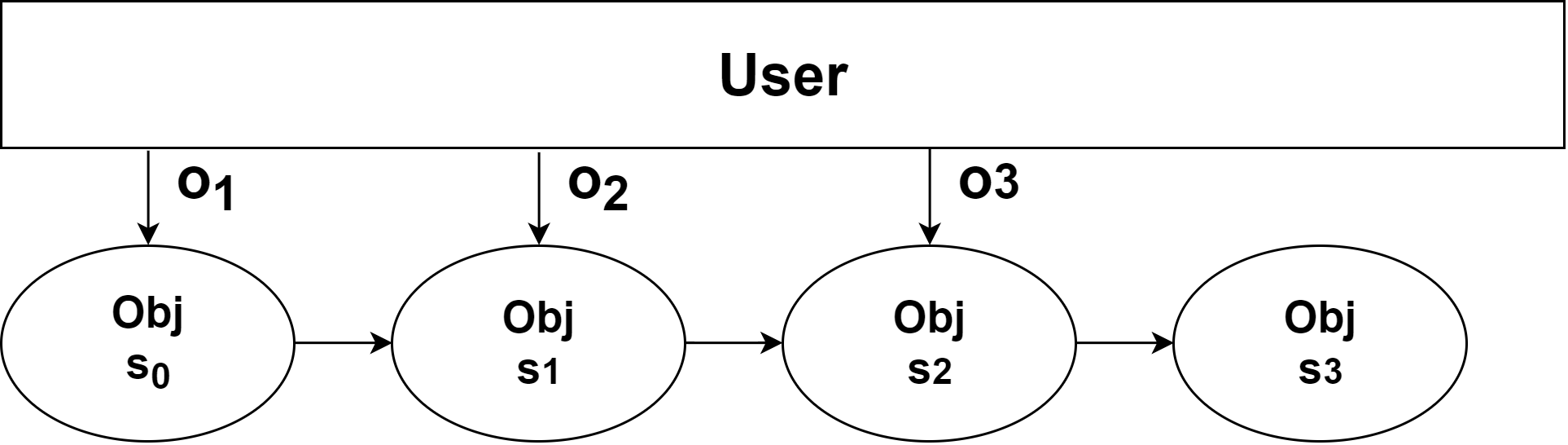
图1. 用户操作改变被操作对象的状态
由上图可知,用户对 O b j Obj Obj 进行了 3 次操作,使得 O b j Obj Obj 的状态从 s 0 s_0 s0 转换到了 s 3 s_3 s3。此时若用户在 s 3 s_3 s3 状态进行撤销,应当使得用户执行有限次撤销,使得用户可以使 O b j Obj Obj 回到 s 1 , s 2 , s 3 s_1,s_2,s_3 s1,s2,s3 中的任意状态(如图2所示)。 这就是撤销功能要实现的需求。
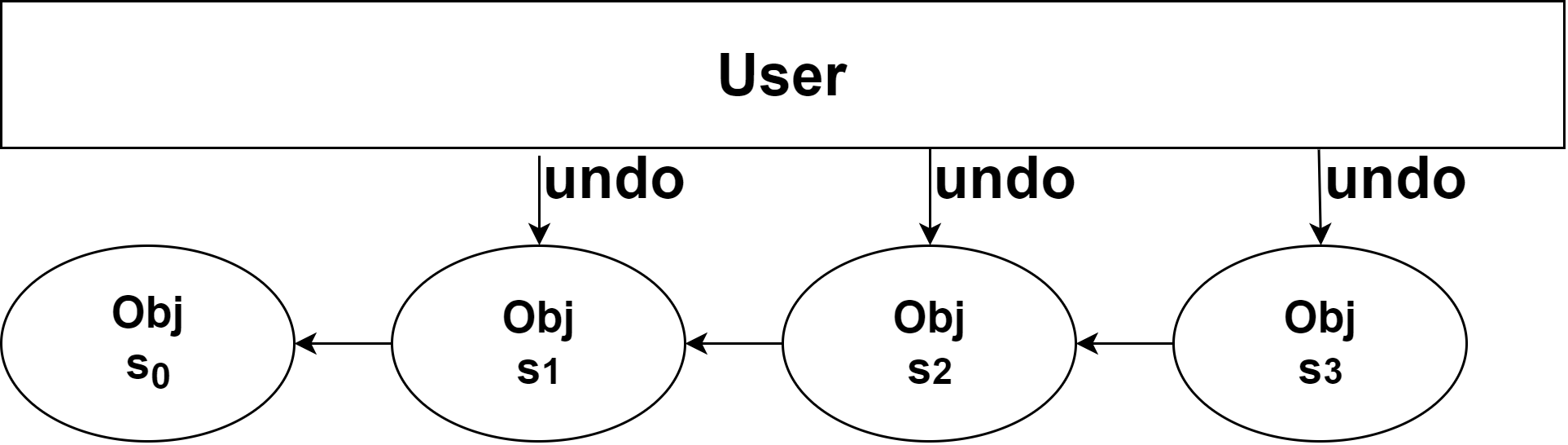
图2. 用户执行撤销操作,回到先前被操作对象的状态
2. 重做 Redo
重做则是在上述撤销的基础上再进行的操作。若用户已经执行了有限次撤销操作,使得 O b j Obj Obj 从状态 s k , ( 0 ≤ k ≤ n ) s_k,(0leq kleq n) sk,(0≤k≤n) 到达了状态 s j , ( 0 ≤ j ≤ k ) s_j,(0leq jleq k) sj,(0≤j≤k),此时可执行有限次重做,可使得 O b j Obj Obj 到达 s j s_j sj 至 s k s_k sk 之间的任意状态。
例如,若在图2所示的情况下。用户在 O b j Obj Obj 的 s 3 s_3 s3 状态下,执行了 3 次撤销操作,回到了状态 s 0 s_0 s0。此时用户应当可以执行有限次重做使得 O b j Obj Obj 可以回到 s 3 , s 2 , s 1 s_3,s_2,s_1 s3,s2,s1 的任意状态。
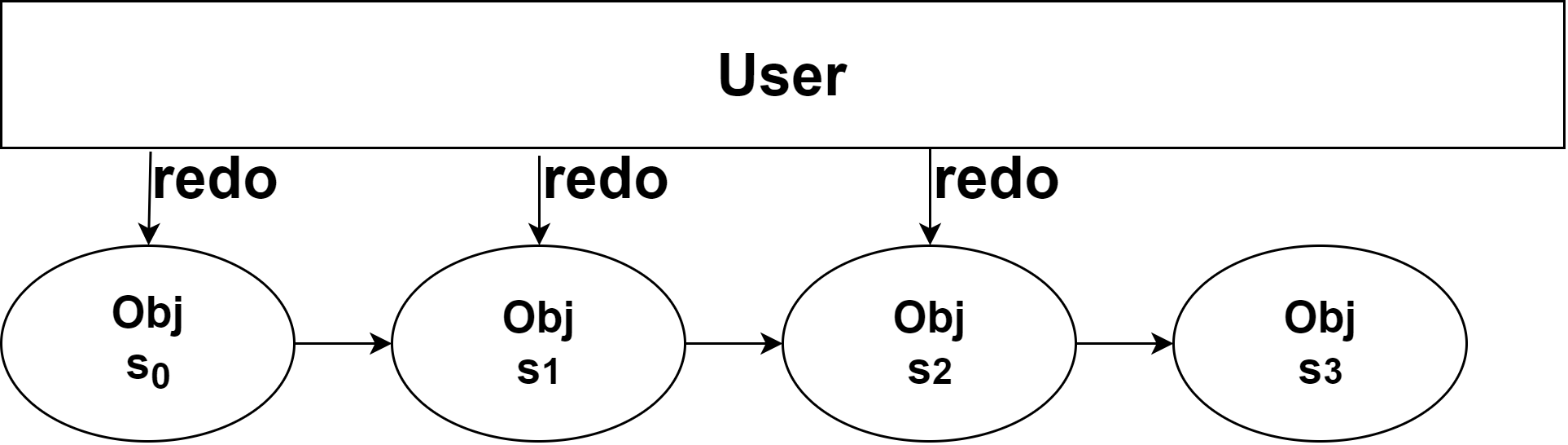
图3. 在图 2 的基础上进行重做操作
3. 综合情况
- 用户进行多次操作后,再进行一定次数的撤销,再进行操作时,会对被操作对象产生新的状态覆盖原来的状态。如图 4 所示。
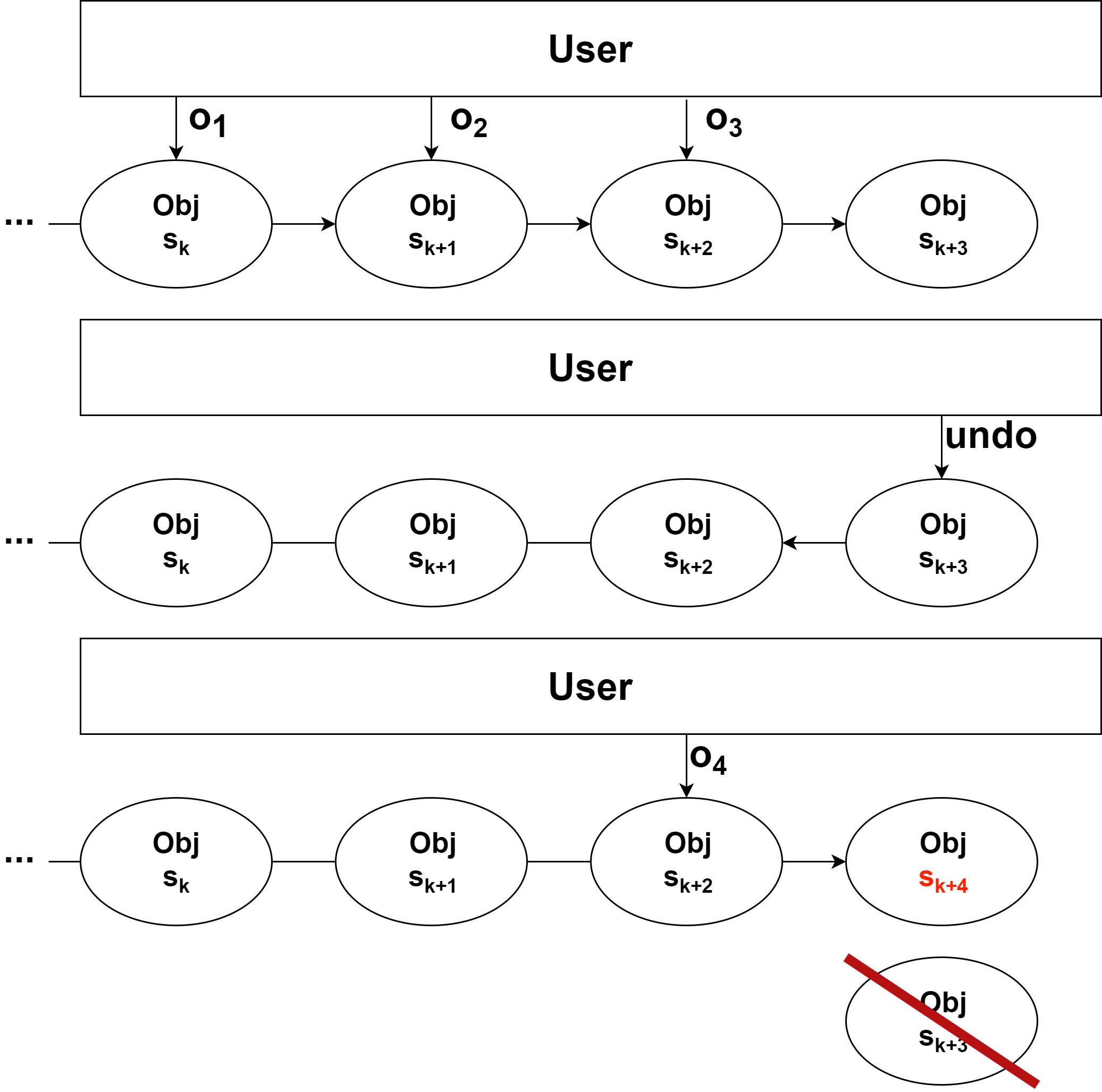
图4. 操作 - 撤回 - 操作的情况
在这种情况下,新操作产生的状态 s k + 4 s_{k+4} sk+4 会覆盖原有的状态 s k + 3 s_{k+3} sk+3,且原 s k + 3 s_{k+3} sk+3 状态的数据会被清除。所以在这种情况下,是不能进行重做的,且无法再通过撤销或重做再获得被清除的状态。
为了实现撤销与清除,可以使用两种较为简单的数据结构进行实现。
三. 双栈法实现
所谓双栈法,顾名思义就是使用两个栈结构来实现模型。基本实现规则有以下几点
- 模型分为两个栈,一个为操作栈,一个为撤销栈。
- 每一个状态都为一个栈元素。
- 每一个操作都产生一个状态栈元素并入栈。
- 操作栈初始含有被操作对象的初始状态 s 0 s_0 s0,撤销栈初始为空。
- 被操作对象的当前状态为栈顶元素元素。
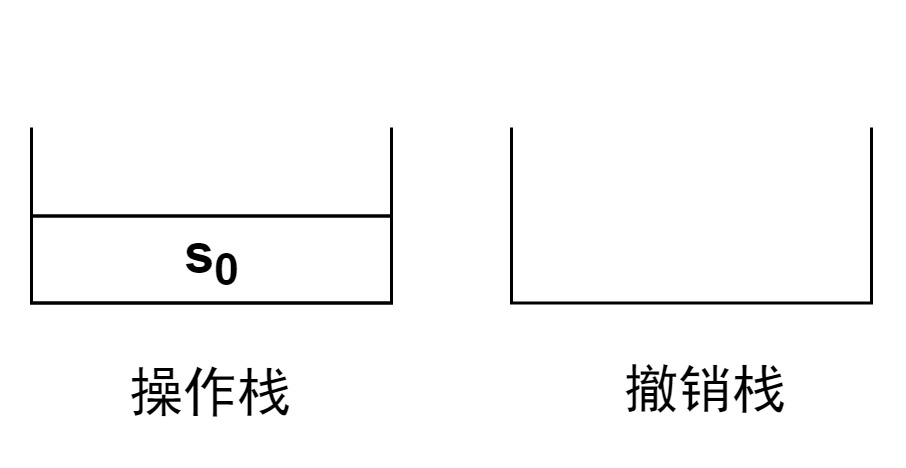
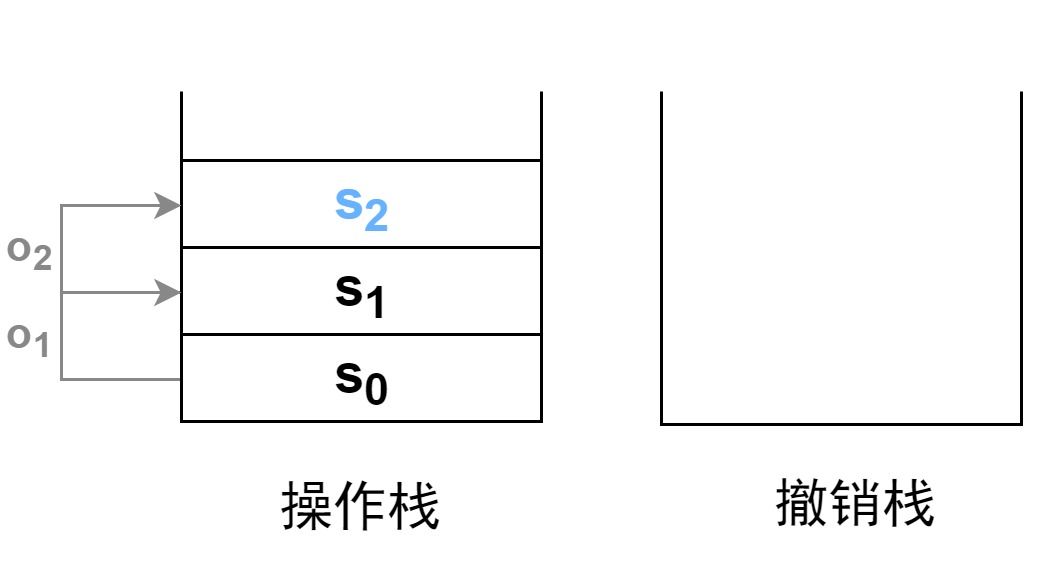
假设我们已经进行了两次操作,在操作栈中压入了三个状态。蓝色的为栈顶元素,是被操作对象的当前状态。
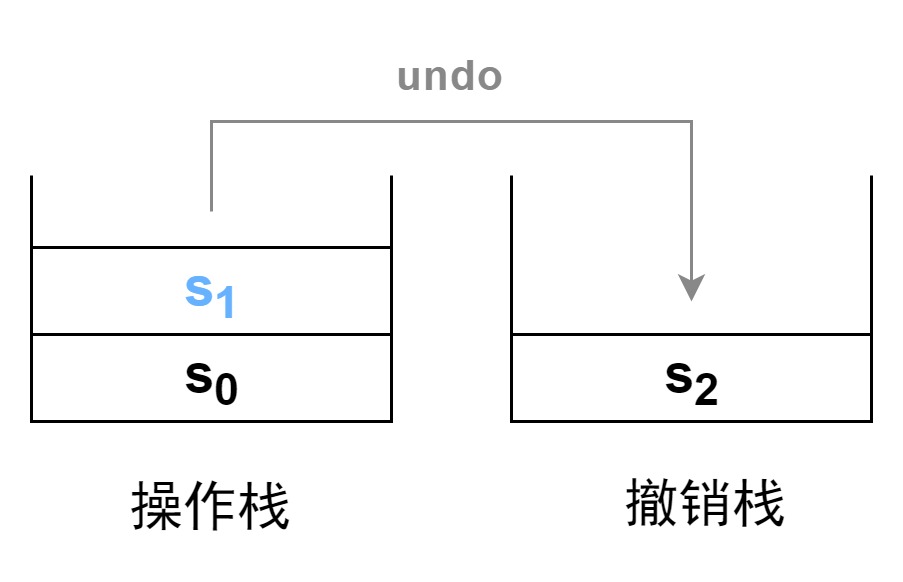
现在我们进行一次撤销操作。在操作栈中弹出栈顶元素 s 2 s_2 s2,将弹出的 s 2 s_2 s2 再压入到撤销栈中。此时完成一次撤销。此时被操作对象的状态转变为了栈顶的 s 1 s_1 s1,完成了撤销。
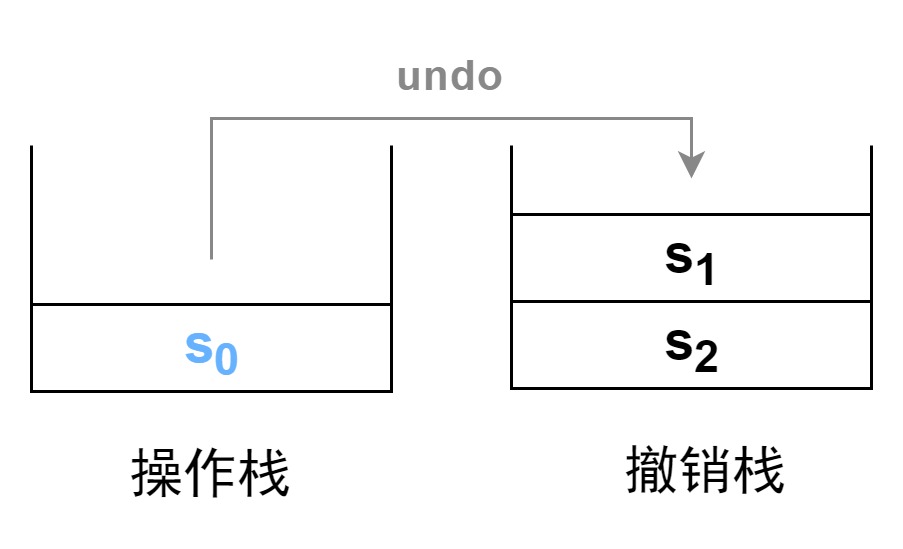
我们继续进行撤销。在操作栈中弹出栈顶元素 s 1 s_1 s1,将弹出的 s 1 s_1 s1 压入撤销栈。此时被操作对象的状态转变为了栈顶的 s 0 s_0 s0。此时不能再继续进行撤销了,因为操作栈不能为空(被操作对象必须拥有一个状态, s 0 s_0 s0已为初始状态)。
此时进行重做测试。进行一次重做,在撤销栈中弹出栈顶元素 s 1 s_1 s1 ,并将 s 1 s_1 s1 压入操作栈。此时被操作对象的状态重新指向 s 1 s_1 s1。完成重做操作。
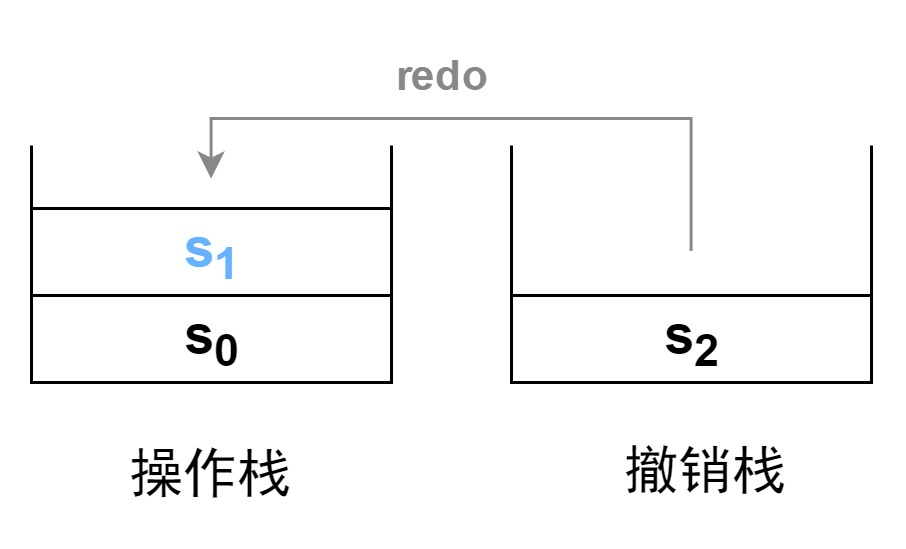
我们接下来再进行一次操作,产生状态
s
3
s_3
s3。此时,如上文综合情况一致。先将新操作产生的状态
s
3
s_3
s3 压入操作栈,然后将撤销栈清空。
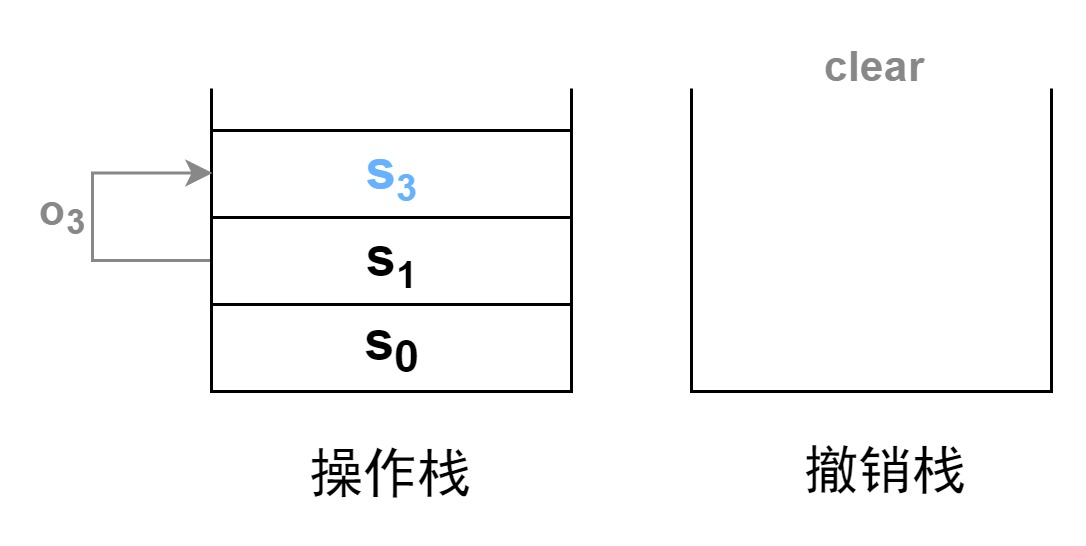
上述描述了一系列操作下双栈模型的情况。对于双栈模型的优缺点有以下几点
-
优点
- 实现简单,能够快速建立模型并实现。
- 可以通过撤销操作回溯到初始状态。
-
缺点
- 无论执行多声步操作都会将状态对象缓存进栈,操作数大的情况下,极度耗费内存空间。
例如,不撤回重做的进行 10000 次操作,每个 s i , ( i = 1 , . . . , 10000 ) s_i,(i=1,...,10000) si,(i=1,...,10000) 用状态类的对象表示,每个对象需要 64 B 的内存,则双栈模型要为该被操作对象缓存 625 Kb 的数据。
- 大多数时候并不需要回溯到初始状态。为了保存足够的状态以保证能够回溯到初始状态非常浪费内存资源。
- 要通过撤销或重做回退 n 步,就需要进行 n 次撤销或重做。(如果使用链栈可以避免该缺点)
- 无论执行多声步操作都会将状态对象缓存进栈,操作数大的情况下,极度耗费内存空间。
为了解决以上缺点,我们可以使用双链表模型。接下来介绍用双链表法优化撤销重做算法。
四. 链表法实现
和双栈法相比,在双链表模型下的撤销和重做更符合许多软件中的设计。我们以 Photoshop 中的历史记录功能为例,来描述。
可见,Ps 的历史记录栏与双栈模型中的初始情况是相似的,都先保存了一个初始状态,Ps 中是新建状态,在双栈中是
s
0
s_0
s0。
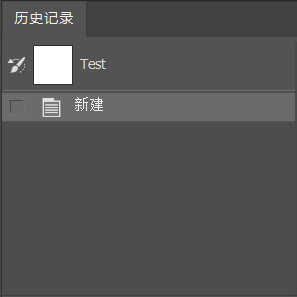
我们若执行多步操作,情况如下。注意,在该历史记录栏中显示的操作名称,而不是状态!其程序背后保存的依然为图像(被操作对象)的状态。
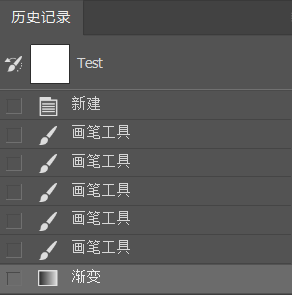
此时我们可以直接通过选择撤回到特定的位置完成多步撤销。并且撤销经过的步骤(灰色的操作名称)也是可以被选择,从而实现重做的。
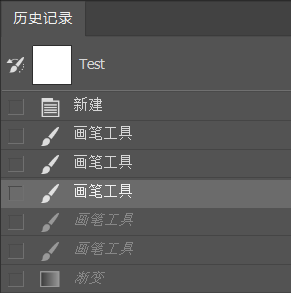
接着,若我们进行新操作,先前的撤销经过的步骤都消失了。这与双栈模型中综合情况相同,会删除用于重做的状态,并使得无法进行重做。
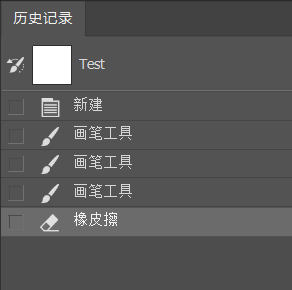
Ps 的历史记录有一个特点,与双栈模型不同,历史记录中不会无休止的将用户的操作记录下去。双栈模型也正是因为会一直将用户操作产生的状态对象进行缓存,所以存在浪费内存资源的缺点。在我们对图像使用很多次画笔工具后,可以发现原来的初始状态操作 “新建” 已经不在了。历史记录栏只缓存特定数量的操作状态,一旦达到数量上限,还有新操作发生,则从最早的操作状态开始删除,同时加入新操作状态到历史记录栏中。这使得内存的消耗是可控的,由状态对象的大小和最大缓存多少状态对象决定。
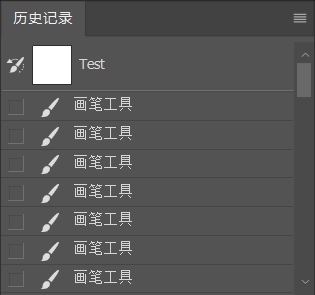
注意右侧的滑动条滑到了最顶部的位置
从以上描述的历史记录栏来说,我们可以使用链表来进行撤销与重组的模型设计。下图为在链表模型中执行各种操作的情况,读者可以按顺序阅览,理解模型的运行情况。
- 其中蓝色的箭头是一个指针,其作用是标识被操作对象当前的状态,因此要进行撤销与重做只需要移动该指针并取出指针所指的状态并以此刷新被操作对象就可以完成。
- 涉及到删除状态时,也只需将指针指向的状态对象的下一节点(链表数据结构的特点)直接置空就可以完成。这一特点接下来有更详细的解释说明。
- 下列图示中的链表规定最大容纳 4 个状态对象。
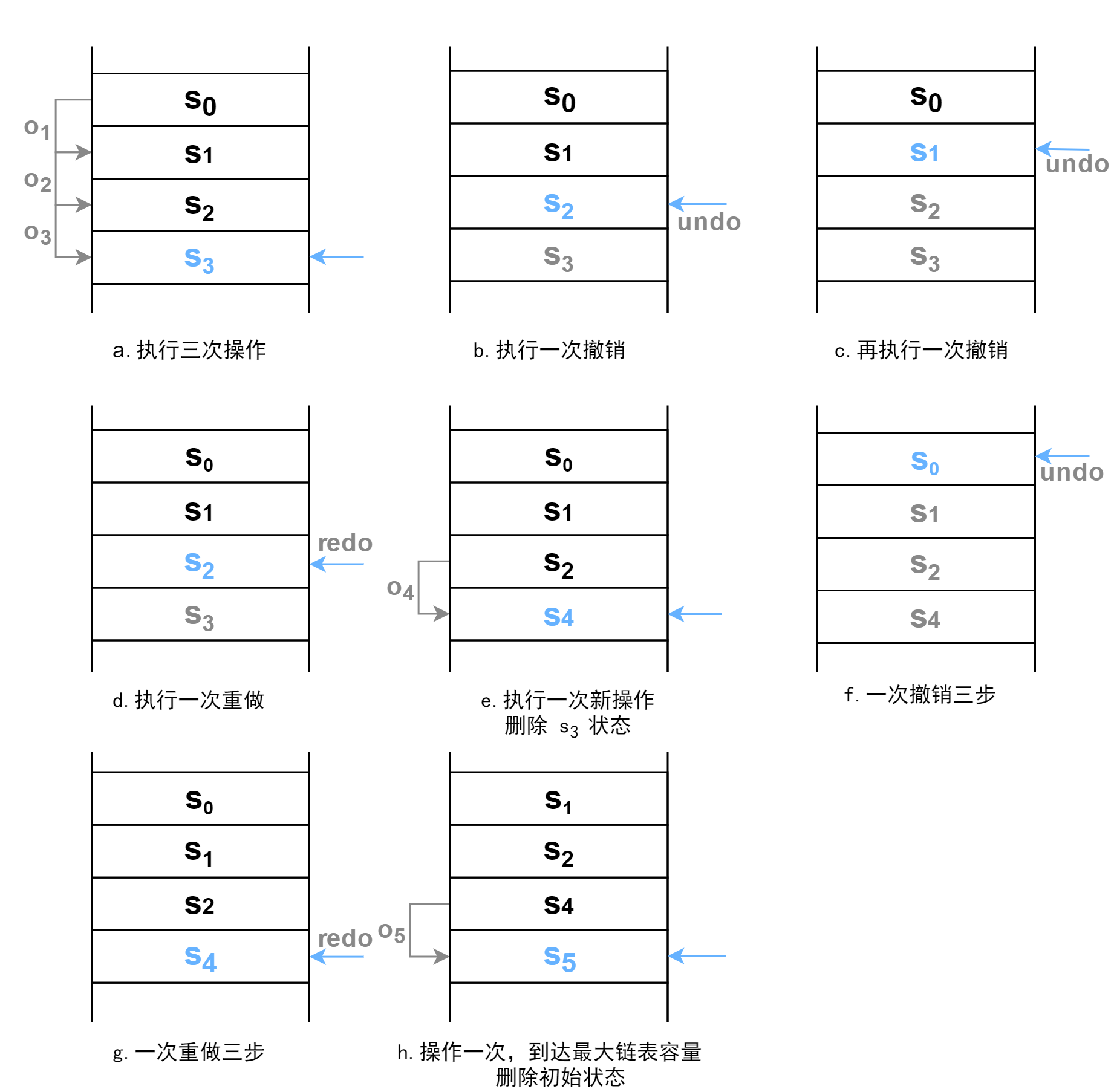
在上图中的 f 情况下,如果我们直接进行新操作,那么缓存的状态 x 1 x_1 x1、 x 2 x_2 x2、 x 4 x_4 x4 都要删除,此时链表的优势就体现出来了。只需要将指针指向的 s 0 s_0 s0 的下一个节点置为新操作产生的状态,就同时完成了删除三个状态与加入新状态了。
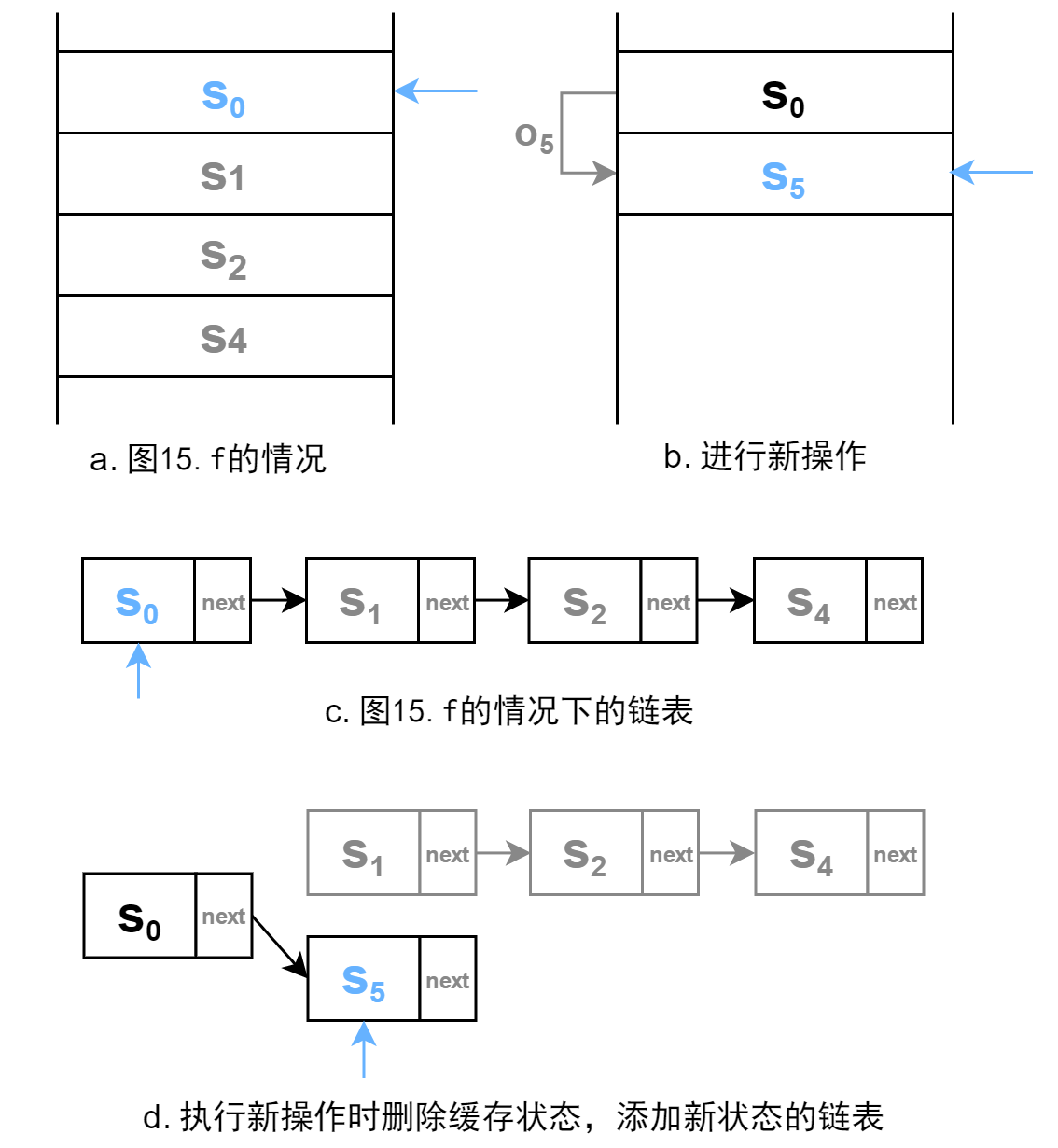
图16. 该模型使用链表数据结构的优势
问题
图15 中的不都是线性存储的列表吗,而且使用线性表就可以完成模型功能无论是顺序存储还是链式存储。为什么要用链表呢?
实际上,确实只要使用线性表就可以完成该模型,但是使用链式存储的链表效率更高。在该模型中,不强调对表中元素的检索,更强调在表的首尾增加元素和删除元素,所以使用链式存储的表会更高效。
五. 结束语
其实这篇博客并不好写,原来是打算草草的随便写一下。但是最后还是因为比较重视数据结构与算法的部分,还是做了很多图,尽量做成教学级别的博客。博客中可能还存在一些语句不通顺或者谬误,欢迎在评论区指出,我会尽快改正。
其次,关于代码。本来是打算附上 Java 实现的代码的。但是由于大学期末,事情比较繁重,先搁置一段时间。后续会在本博客更新实现代码。如果喜欢博客的内容,期望得到代码的话,欢迎收藏关注。
六. 提示
可以学习设计模式中的备忘录模式。其与本博客讨论的撤销与重做非常相似,或者说完全相同,只是更具体的设计实现。
最后
以上就是无辜花生最近收集整理的关于【数据结构】撤销与重做 | 模型实现撤销与重做 | 模型实现的全部内容,更多相关【数据结构】撤销与重做内容请搜索靠谱客的其他文章。








发表评论 取消回复