假如设计好了一个控制器,得到了它的传递函数,那么该怎么在单片机中实现它呢?里面都是微积分,该怎么编程呢?这就要设计到传函的离散化了。
1:离散化
1.1、离散化的目的
- 将s域下的传递函数转换为离散的z域函数;
- 将离散域下的函数转化为差分方程,然后在单片机中实现;
1.2、离散化的方法
常用的离散化方法有:
- 前向差分法;
- 后向差分法:
- 双线性变换法;
- 零阶保持器法;
- 一阶保持器法;
- 脉冲响应不变法;
前三种方法比较简单,传递函数中,直接用 z和s的关系进行替换就行:
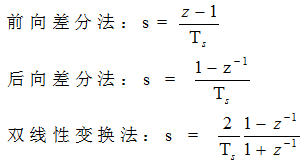
其中Ts为离散化采样时间。
可以借助matlab工具进行离散化,matlab提供多种离散化的方法;
dsys=c2d(sys,ts,’method’); % 传函离散,其中ts表示离散的采样周期,method表示离散的方法;sys表示s域传函,dsys表示对应的z域传函;
其中method包括以下几种方法:
- zoh 零阶保持器;
- foh 一阶保持器;
- tustin 双线性变换法;
- matched 零极点匹配法;
- impulse 脉冲响应不变法;
1.3、使用不同离散化方法的影响
下面我们首先使用不同离散化方法对传函G(s) = 1/(0.2s+1)进行离散,离散化采样时间Ts=0.05:

然后对比不同离散化方法后的伯德图和未离散化的系统伯德图:
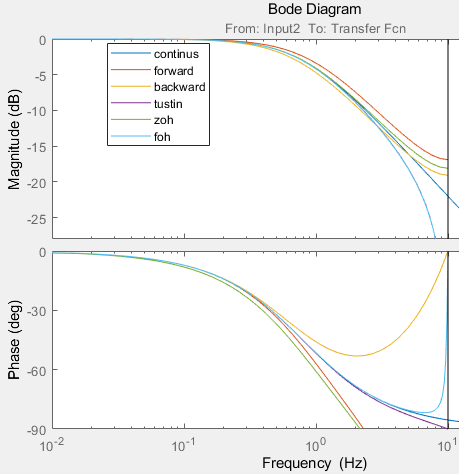
从伯德图中可以看出,前向差分法离散化以后偏离实际的系统更远,不能保证系统的稳定性。而
后向差分法和双线性变换法,更接近未离散化的伯德图,所以后向差分法和双线性变换法在工程中较为常用。
2:传函到单片机实现的例子
假设一个低通滤波器的传函为:
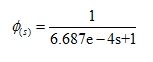
我们先用matlab工具看下他的特性;
>> num=1;
den=[6.687e-4,1];
sys=tf(num,den);
p=bodeoptions;
p.FreqUnits= 'Hz';
bode(sys,p)
看下他的伯德图:
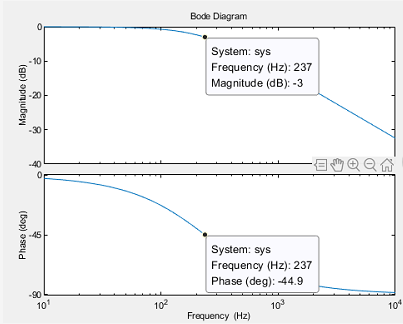
从图中可以看到该低通滤波器截止频率为237Hz,截止频率处的相移位45度;
我们也用simulink搭建一个仿真,验证下当该滤波器输入一个237HZ的正弦波时,输出是不是一个为-3dB衰减,且相移45度的正弦波;
仿真如下:
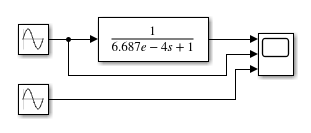
波形如下:
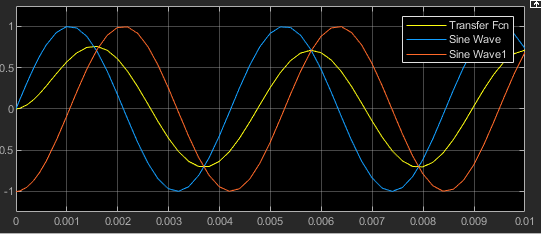
图中sine ware和sin wave1两个波形是相差90度的,而滤波出来的Transfer Fcn波形可以正好相差45度,衰减-3dB;
我们现在用matlab对他进行离散化
num=1;
den=[6.687e-4,1];
sys=tf(num,den);
ts=64e-6;
>>
dsys=c2d(sys,ts,'z') % 注意连续转离散(c2d),和离散转连续(d2c)的用法
dsys =
0.09127
----------
z - 0.9087
然后我们用simulink再搭建他对应的离散传函下的系统特性有没有变化;
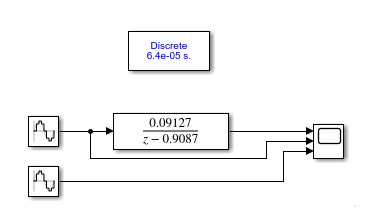
采样时间为ts=64e-6;
波形如下:
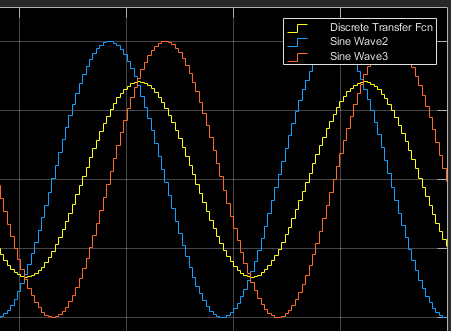
从图中可以看出滤波出来的DiscreteTransfer Fcn波形正好相差45度,衰减-3dB;所以他的离散下的特性没变;
下面将离散域下的函数转化为差分方程
假设输入为x,输出为y;

转化为上面的差分方程后,就可以在单片机中实现了,我们也可以在simulink中用sfun仿真;
看下转化为数字滤波后的特性是否发生变化。同样输入赋值为1,频率为237HZ的正玄波。
仿真如下:
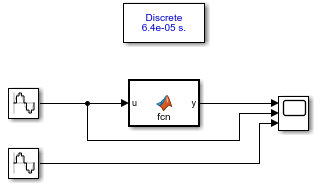
sfun如下:
function y = fcn(u)
persistent yl;
%定义一个静态变量
if isempty(yl)
%给静态变量赋初值
yl=0;
end
persistent ul;
if isempty(ul)
ul=0;
end
y=0.9086*yl+0.09136*ul;
yl=y;
ul=u;
仿真波形如下:
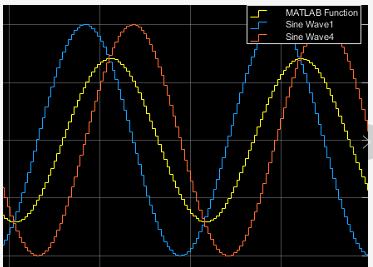
从图中可以看出滤波出来的MATLAB Function波形正好相差45度,衰减-3dB;
注意:可能有的人会问,一阶低通滤波器的差分方程的形式不应该是 :
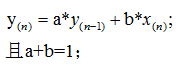
是的。这个是用一阶后项差分法离散后得出的差分方程;
因为没有找到,matlab中传函怎么进行一阶后项差分离散(也就是用
s
=
1
−
z
−
1
T
s
s=frac{1-z^{-1}}{Ts}
s=Ts1−z−1替代);
其实我们也可以定义符号变量进行替代。
>> syms s z Ts;%定义符号变量
s=(1-z^-1)/Ts;%一阶后项差分
sys=1/(s+1);
subs(sys,[s],[z])%传递函数中用z替代s
ans =
-1/((1/z - 1)/Ts - 1) %这里我们可以对符号表达式进行各种化简
%参见matlab符号表达式的化简常用命令函数
simplify(ans) %对结果进行化简
ans =
(Ts*z)/(z + Ts*z - 1)
>> pretty(ans)%美化下结果
Ts z
------------
z + Ts z - 1
化成差分方程的形式:
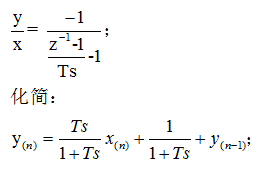
以上整个就是传函的离散化的单片机实现的过程了。
对于二阶以上的传递函数,我们当然也可以采用以上同样的方法进行离散化,但是我们常常采用另外一种方法就行离散化,这种方法离散化显得更加简单。可以参考:传递函数的离散化(二)—— C实现
最后
以上就是沉默果汁最近收集整理的关于传递函数的离散化(一)—— C实现的全部内容,更多相关传递函数的离散化(一)——内容请搜索靠谱客的其他文章。








发表评论 取消回复