几类常微分方程的matlab求解方法 | 刚性微分方程、隐式微分方程、微分代数方程目录微分方程的转换刚性微分方程求解隐式微分方程求解微分代数方程求解

80 阅读 0 评论 53 点赞

我是靠谱客的博主无语豌豆，最近开发中收集的这篇文章主要介绍几类常微分方程的matlab求解方法 | 刚性微分方程、隐式微分方程、微分代数方程目录微分方程的转换刚性微分方程求解隐式微分方程求解微分代数方程求解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

微分方程的转换

根据微分方程求解的标准型，要得到微分方程的数值解，应该先将该方程变换成一阶常微分方程组。

一、单个高阶常微分方程

1、原状态

高阶常微分方程一般形式：

$gif.latex?y^{(n)}=f(t,y,y{}',...,y^{(n-1)})$

初值为y(0),y'(0),...,y^(n-1)(0)

2、变换后

可以选择一组状态变量x1=y,x2=y',...,xn=y^(n-1)，可以将原方程变换为一阶方程组形式：

x'1=x2
x'2=x3
...
x'n=f(t,x1,x2,...,xn)

初值为x1(0)=y(0),x2(0)=y'(0),...,xn(0)=y^(n-1)(0)

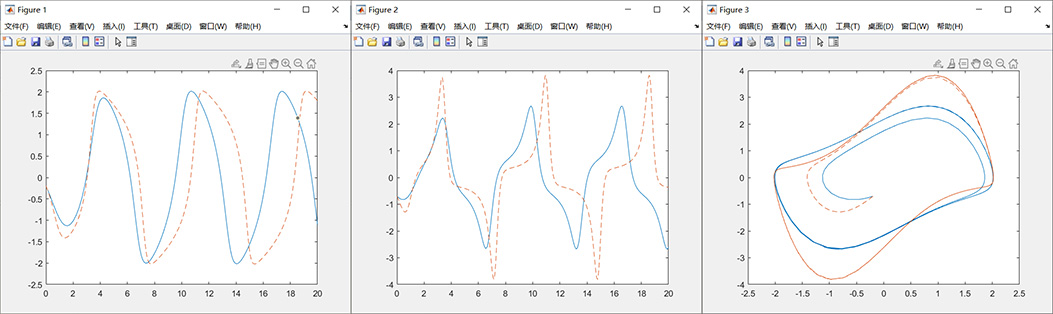
例1.1 求y''+mu*(y^2-1)*y'+y=0，初值为y(0)=0.2,y'(0)=-0.7

代码如下：

%% 单个高阶常微分方程处理方法
f=@(t,x,mu) [x(2);-mu*(x(1)^2-1)*x(2)-x(1)];% 带附加参数的匿名函数
x0=[-0.2;-0.7];
tn=20;mu=1;
tic; % tic，toc记录时间
[t1,y1]=ode45(f,[0,tn],x0,[],mu);
toc;
mu=2;
tic;
[t2,y2]=ode45(f,[0,tn],x0,[],mu);
toc;
figure(1);
plot(t1,y1(:,1),t2,y2(:,1),'--');
figure(2);
plot(t1,y1(:,2),t2,y2(:,2),'--');
figure(3);
plot(y1(:,1),y1(:,2),y2(:,1),y2(:,2),'--');
% 绘制相平面图
% mu=1000，tn=3000，x0=[2;0]时,未出现内存不够的情况,但用求解刚性微分方程的方式计算量小得多
% options=odeset('RelTol',1e-4,'AbsTol',[1e-4 1e-4 1e-5]);是解微分方程时的选项设置
% 'RelTol',1e-4,是相对误差设置，'AbsTol',[1e-4 1e-4 1e-5]是绝对误差设置
f=@(t,x,mu) [x(2);-mu*(x(1)^2-1)*x(2)-x(1)];
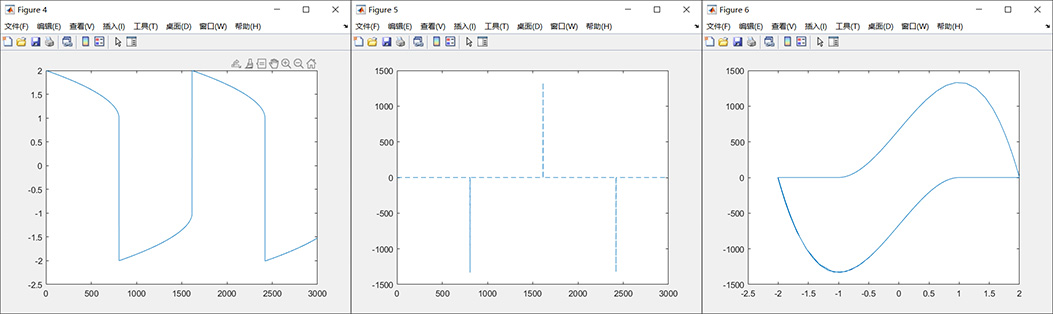
x0=[2;0];tn=3000;
mu=1000;
tic;
options=odeset('RelTol',1e-10,'AbsTol',1e-10);
[t3,y3]=ode45(f,[0,tn],x0,[],mu);toc;figure(4);
plot(t3,y3(:,1));
figure(5);
plot(t3,y3(:,2),'--');
figure(6);
plot(y3(:,1),y3(:,2)); %绘制相平面图

运行结果：

mu=1和mu=2时，实线为[t,y]；虚线为[t,y']；用时分别为 0.002099 秒和0.001892 秒。

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

mu=1000，tn=3000，x0=[2;0]时，实线为[t,y]；虚线为[t,y']；用时为28.018461 秒。

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

注：用ode45()计算mu=1000，tn=3000，x0=[2;0]时的方程，如果电脑内存不够的话会报错，因为步长过小导致，可采取刚性方程的算法，用ode15s可大大减小计算量。

二、高阶常微分方程组

1、原状态

如果可以显式地将两个方程写成：

$gif.latex?x^{(m)}=f(t,x,x',...,x^{(m-1)},y,y',...y^{(n-1)})$
$gif.latex?y^{(n)}=g(t,x,x',...,x^{(m-1)},y,y',...,y^{(n-1)})$

初值为y(0),y'(0),...,y^(n-1)(0)

2、变换后

仍然可以选择一组状态变量x1=x,x2=x',...,xm=x^(m-1)，x(m+1)=y,x(m+2)=y',...,x(m+n)=y^(n-1)，可以将原方程变换为一阶微分方程组：

x'1=x2
...
x'm=f(t,x1,x2,...,x(m+n))
x'(m+1)=x(m+2)
...
x'(m+n)=g(t,x1,x2,...,x(m+n))

例1.2 卫星的运动轨迹满足下面方程组：

x''=2*y'+x-mu1*(x+mu)/r1^3-mu*(x-mu1)/r2^3
y''=-2*x'+y-mu1*y/r1^3-mu*y/r2^3

其中，mu=1/82.45,mu1=1-mu,r1=sqrt((x+mu)^2+y^2),r2=sqrt((x-mu1)^2+y^2)

代码如下：

函数程序

function f=c_7_3_fun
% 定义一个接口，通过匿名函数调用
% 通过定义接口的方式，在一个函数文件例里可编写多个函数
f.apolloeq=@apolloeq;
end
% 选择一组状态向量：x1=x,x2=x',x3=y,x4=y'
function dx=apolloeq(t,x)
% 带有附加参数的微分方程描述曲线
mu=1/82.45;
mu1=1-mu;
r1=sqrt((x(1)+mu)^2+x(3)^2);
r2=sqrt((x(1)-mu1)^2+x(3)^2);
dx=[x(2);2*x(4)+x(1)-mu1*(x(1)+mu)/r1^3-mu*(x(1)-mu1)/r2^3;x(4);-2*x(2)+x(3)-mu1*x(3)/r1^3-mu*x(3)/r2^3];
end

主程序

%% 高阶常微分方程组变换方法
f=c_7_3_funx0=[1.2;0;0;-1.04935751];
tic;
[t,y]=ode45(@f.apolloeq,[0,20],x0);
toc;
length(t) % 读取向量长度
plot(y(:,1),y(:,3)); % 绘制相平面图,默认精度不够（0.001）%精度改为1e-5
tic;
[t1,y1]=ode45(@f.apolloeq,[0,20],x0,odeset('RelTol',1e-5));
toc;
length(t1) % 读取向量长度
figure;
plot(y1(:,1),y1(:,3)); %精度改为1e-6
tic;
[t2,y2]=ode45(@f.apolloeq,[0,20],x0,odeset('RelTol',1e-6));
toc;
length(t2) % 读取向量长度
figure;
plot(y2(:,1),y2(:,3));
min(diff(t2)) %计算步长
figure;
plot(t2(1:end-1),diff(t2)); % 绘制实际使用的步长变化曲线
%% 采用定步长四阶RK算法
f=c_7_3_funx0=[1.2;0;0;-1.04935751];
tic;
[t3,y3]=rk_4(@f.apolloeq,[0,20,0.01],x0);
toc;
length(t3) % 读取向量长度figure;
plot(y3(:,1),y3(:,3)); % 步长改为0.001
f=c_7_3_funx0=[1.2;0;0;-1.04935751];
tic;
[t4,y4]=rk_4(@f.apolloeq,[0,20,0.001],x0);toc;length(t4) % 读取向量长度figure;
plot(y4(:,1),y4(:,3)); %在求解常微分方程时建议采用变步长算法

运行结果：（算法比较）

算法：ode45()，默认精度0.001，历时 0.007719 秒，ans =689（向量长度）

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

算法：ode45()，精度1e-5，历时 0.017587 秒，ans =1309（向量长度）

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

算法：ode45()，精度1e-6，历时 0.017856 秒，ans =1873（向量长度），ans =1.8927e-04（最小步长）

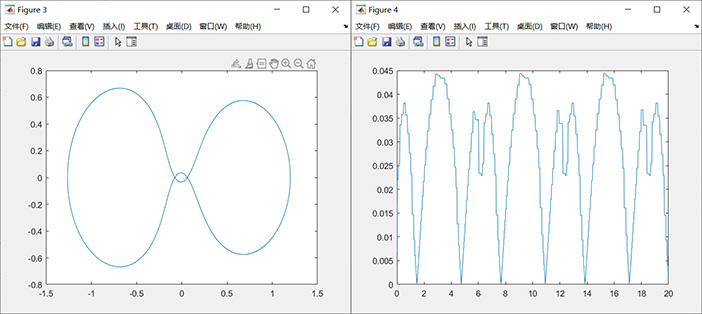
watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

注：改变算法精度重新求解，发现结果是否不同，可以通过此法验证数值解的正确性。

算法：定步长四阶RK算法，步长0.01，历时 0.044436 秒，ans =2001（向量长度）结果错误

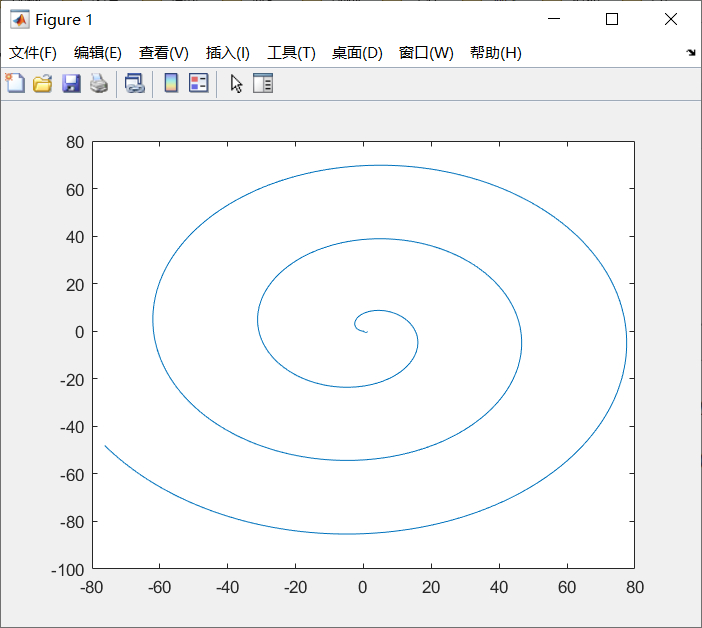
watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

算法：定步长四阶RK算法，步长0.001，历时 0.716064 秒，ans =20001（向量长度）

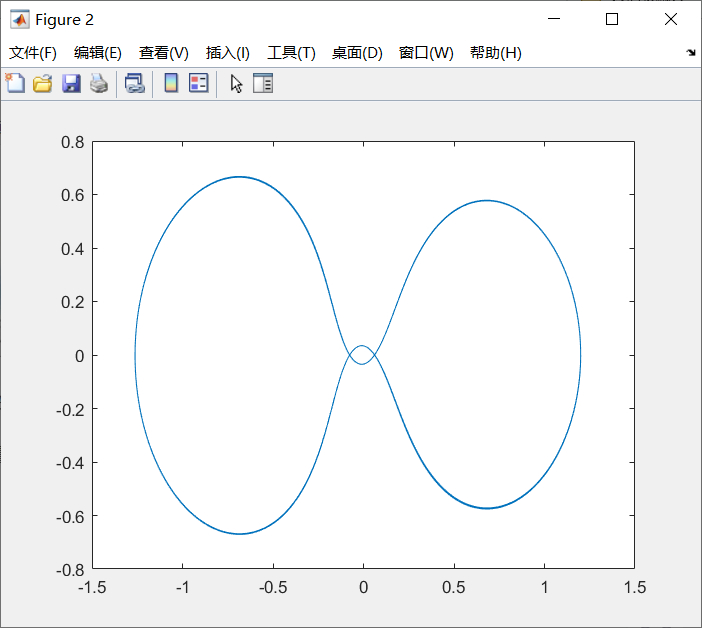
watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

注：定步长四阶RK算法中，当步长减小至0.001时，结果才大致正确，大求解时间明显变长，建议采用变步长算法。

例1.3 将下列方程组转化为一阶微分方程组。

x''+2*y'*x=2*y''
x''*y'+3*x'*y''+x*y'-y=5

代码如下：

%% 高阶微分方程隐式地含有最高项
% 除了手工转化，可以利用MATLAB符号运算工具箱
syms x1 x2 x3 x4 dx dy % 声明符号变量
[dx,dy]=solve([dx+2*x4*x1==2*dy,dx*x4+3*x2*dy+x1*x4-x3==5],[dx,dy])
% 解代数方程
% solve(eqn,var)

运行结果：

dx =(2*(x3 - x1*x4 - 3*x1*x2*x4 + 5))/(3*x2 + 2*x4)
dy =(2*x1*x4^2 - x1*x4 + x3 + 5)/(3*x2 + 2*x4)

注：可以选择手动求解，正常选择状态变量，然后代入法求x''和y''，也可利用solve求代数方程的方法，更高效。

刚性微分方程求解

刚性微分方程：一些解变化缓慢，另一些变化快，且相差悬殊。

注：刚性问题——在用微分方程描述的一个变化过程中，往往又包含着多个相互作用但变化速相差十分悬殊的子过程，这样一类过程就认为具有“刚性”。描述这类过程的微分方程初值问题称为“刚性问题”。例如，宇航飞行器自动控制系统一般包含两个相互作用但效应速度相差十分悬殊的子系统，一个是控制飞行器质心运动的系统，当飞行器速度较大时，质心运动惯性较大，因而相对来说变化缓慢；另一个是控制飞行器运动姿态的系统，由于惯性小，相对来说变化很快，因而整个系统就是一个刚性系统。

例2.1 （例1.1）求y''+mu*(y^2-1)*y'+y=0，初值为y(0)=0.2,y'(0)=-0.7,用刚性方程解法求解mu=1000，tn=3000，x0=[2;0]的情况。

常用求解器：ode15s()

代码如下：

%% 刚性微分方程求解1% 对于刚性问题的求解，ode15s求解速度比ode45效率高得多ff=odeset;ff.RelTol=1e-10;ff.AbsTol=1e-10; % 设置控制精度x0=[2;0];tn=3000;f=@(t,x,mu) [x(2);-mu*(x(1)^2-1)*x(2)-x(1)];mu=1000;tic;[t4,y4]=ode15s(f,[0,tn],x0,ff,mu);toc;length(t4)plot(t4,y4(:,1));figure;plot(t4,y4(:,2),'--');

运行结果：（mu=1000，tn=3000，x0=[2;0]时）

算法：ode15s，实线为[t,y]；虚线为[t,y']；用时为0.064681 秒，取点5917个。

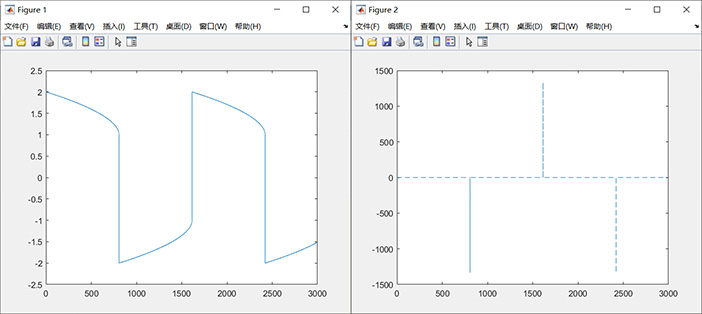
watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

对比组（代码见例1.1）

算法：ode45，实线为[t,y]；虚线为[t,y']；用时为28.018461 秒，取点6757169个。

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

注：1、可见，在对刚性问题的求解中，用专用的刚性求解器（此处为ode15s）能大大提高效率。2、并不是所有刚性问题求解都要刻意选择钢性问题的解法，许多传统的刚性问题采用普通求解方法就可以解出。

例2.2 考虑下列常微分方程

y'1=0.04*(1-y1)-(1-y1)*y1+0.0001*(1-y2)^2
y'2=-10^4*y1+3000*(1-y2)^2

其中，初值为y1(0)=0,y2(0)=1，计算区间为(0,100)，选择适当的方法求数值解。

代码如下：

%% 刚性微分方程求解2% 用ode45求解f=@(t,y)[0.04*(1-y(1))-(1-y(2))*y(1)+0.0001*(1-y(2))^2;...
-10^4*y(1)+3000*(1-y(2))^2]; % 用匿名函数描述微分微分方程tic;[t2,y2]=ode45(f,[0,100],[0;1]);toc;length(t2)figure;plot(t2,y2)% 改用ode15s求解f=@(t,y)[0.04*(1-y(1))-(1-y(2))*y(1)+0.0001*(1-y(2))^2;...
-10^4*y(1)+3000*(1-y(2))^2]; % 用匿名函数描述微分微分方程tic;[t2,y2]=ode15s(f,[0,100],[0;1]);toc;length(t2)figure;plot(t2,y2)% 改用ode15s求解,提高精度ff=odeset;ff.RelTol=1e-10;ff.AbsTol=1e-10; % 设置控制精度f=@(t,y)[0.04*(1-y(1))-(1-y(2))*y(1)+0.0001*(1-y(2))^2;...
-10^4*y(1)+3000*(1-y(2))^2]; % 用匿名函数描述微分微分方程tic;[t2,y2]=ode15s(f,[0,100],[0;1],ff);toc;length(t2)figure;plot(t2,y2)

运行结果：

分别采用ode45、ode15s、提高精度后的ode15s求解。

ode45（默认精度0.001）：历时 0.486060 秒，ans = 356941（点数）

ode15s（默认精度0.001）：历时 0.003206 秒，ans =56（点数）

ode15s（1e-10）：历时 0.012131 秒，ans =614（点数）

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

隐式微分方程求解

隐式微分方程：不能转换成一阶显式微分方程的微分方程。

常用求解器：ode15i()，ode15s()（代数方程）

解法：

1、矩阵法

例3.1 给定隐式微分方程组，已知x1(0)=x2(0)=0，求数值解。

x'1*sin(x1)+x'2*cos(x2)+x1=1
-x'1*cos(x2)+x'2*sin(x1)+x2=0

解：将其改写成矩阵形式A(x)*x'=B(x)

A(x)=[sin(x(1)) cos(x(2));-cos(x(2)) sin(x(1))]
B(x)=[1-x(1);-x(2)]

假设A(x)为非奇异矩阵，则x'=A(X)^(-1)*B(x)（该方法只适合A(x)为非奇异矩阵的情况）

代码如下：

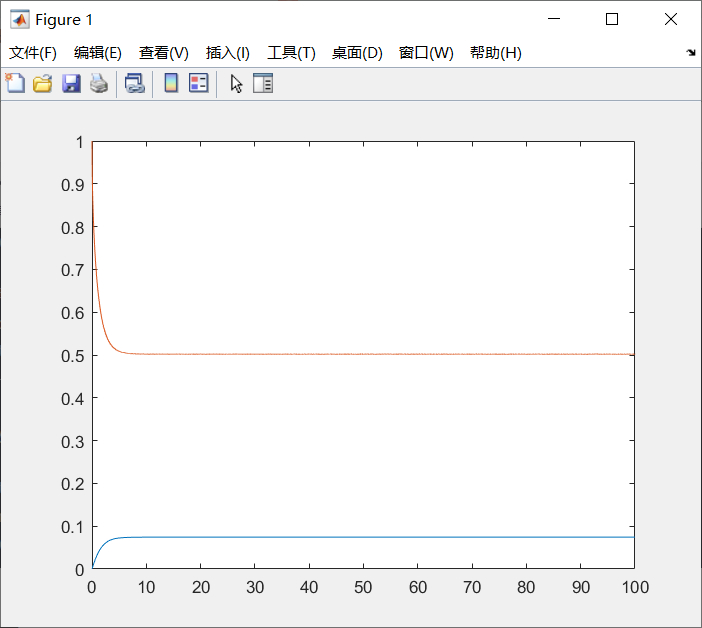
%% 隐式微分方程求解% 若得不到奇异矩阵的报错，则正确f=@(t,x)inv([sin(x(1)) cos(x(2));-cos(x(2)) sin(x(1))])*[1-x(1);-x(2)];% inv矩阵求逆opt=odeset;opt.RelTol=1e-6;[t,x]=ode45(f,[0,10],[0;0],opt);plot(t,x)% 此解法有隐患，参照代数方程解法可以更好的求解

运行结果：

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

注：此解法有隐患（需要非奇异矩阵的条件），参照下一章 “代数方程解法” 可以更好的求解（例4.2）

2、巧用代数方程

例3.2 考虑下列复杂隐式方程

x''sin(y')+y''^2=-2*x*y*e^(-x')+x*x''*y'
x*x''*y''+cos(y'')=3*y*x'*e^(-x)

选定状态变量x1=x,x2=x',x3=y,x4=y'，设p1=x'',p2=y''，原方程组变为：

p(1)*sin(x(4))+p(2)^2+2*x(1)*x(3)*exp(-x(2))-x(1)*p(1)*x(4)=0
x(1)*p(1)*p(2)+cos(p(2))-3*x(3)*x(2)*exp(-x(1)) =0

代码如下：

函数程序

function f=c_7_3_fun% 定义一个接口，通过匿名函数调用% 通过定义接口的方式，在一个函数文件例里可编写多个函数%f.apolloeq=@apolloeq;f.c7impode=@c7impode;endfunction dy=c7impode(t,x) % x为参数dx=@(p,x) [p(1)*sin(x(4))+p(2)^2+2*x(1)*x(3)*exp(-x(2))-x(1)*...
p(1)*x(4);x(1)*p(1)*p(2)+cos(p(2))-3*x(3)*x(2)*exp(-x(1))];
% 用x1,x2,x3,x4表示p1,p2ff=optimset;ff.Display='off';% Level of display (see Iterative Display):
% 'off' or 'none' displays no output.
% 'iter' displays output at each iteration,
%
and gives the default exit message.
% 'iter-detailed' displays output at each iteration,
%
and gives the technical exit message.
% 'final' (default) displays just the final output,
%
and gives the default exit message.
% 'final-detailed' displays just the final output,
%
and gives the technical exit message.dx1=fsolve(dx,x([1,3]),ff,x);
% x = fsolve(fun,x0,options)
% fsolve求解非线性方程，初值选择p1(0)=x1,p2(0)=x3,加快代数方程收敛速度和精度
% x作为已知附加参数给出，得出结果为p1,p2dy=[x(2);dx1(1);x(4);dx1(2)];
% dy=[x2=x',dx1(1)=p1=x'',x4=y',dx1(2)=p2=y'']
% 求ode对应的解为[x,x',y,y']end

主程序

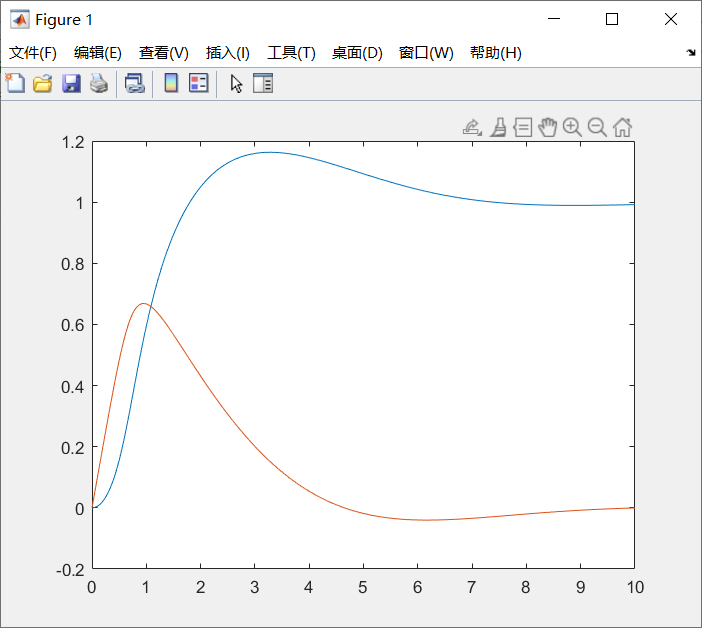
%% 复杂隐式微分方程f=c_7_3_fun[t,x]=ode15s(f.c7impode,[0,2],[1,0,0,1]);% x1随t变化的图像figure(1);plot(t,x(:,1));% x2随t变化的图像figure(2);plot(t,x(:,2));% x3随t变化的图像figure(3);plot(t,x(:,3));% x4随t变化的图像figure(4);plot(t,x(:,4));% x随t变化的总图像figure(5);plot(t,x);% 下面代码找不到显式解（方程和系统求解器无解）% syms x1 x2 x3 x4 dx dy % 声明符号变量% [dx,dy]=solve([dx*sin(x4)+dy^2+2*x1*x3*exp(-x2)-x1*...%
dx*x4==0,x1*dx*dy+cos(dy)-3*x3*x2*exp(-x1)==0],[dx,dy])

运行结果：

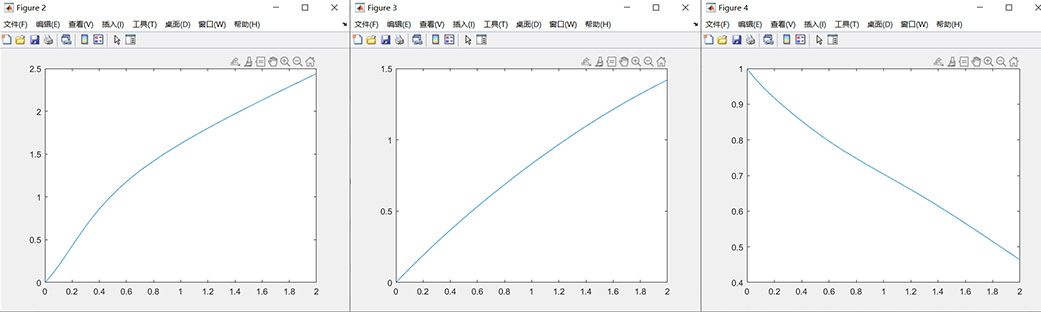
watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

3、直接用ode15i()函数求解

求解之前需要给出（x0,x'0），不能随意赋值，只能有n个是独立的，其余的需要用隐式方程求解，否则将出现矛盾的初始条件，用decic()函数能的处相容的初值。

例 3.3 （例3.2）考虑下列复杂隐式方程

x''sin(y')+y''^2=-2*x*y*e^(-x')+x*x''*y'
x*x''*y''+cos(y'')=3*y*x'*e^(-x)

选定状态变量x1=x,x2=x',x3=y,x4=y'，原方程组变为隐式方程标准型：

x'1-x2=0
x'2*sin(x4)+x'4^2+2*e^(-x2)*x1*x3-x1*x'2*x4=0
x'3-x4=0
x1*x'2*x'4+cosx'4-3*e^(-x1)*x3*x2=0

代码如下：

%% 利用ode15i()求解复杂隐式微分方程% 隐式微分方程的描述f=@(t,x,xd)[xd(1)-x(2);
xd(2)*sin(x(4))+xd(4)^2+2*exp(-x(2))*x(1)*x(3)-x(1)*xd(2)*x(4);
xd(3)-x(4);
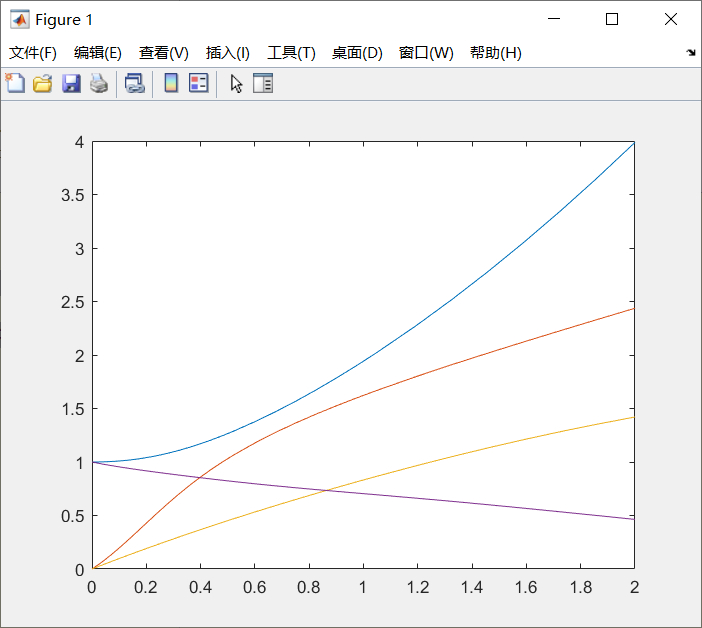
x(1)*xd(2)*xd(4)+cos(xd(4))-3*exp(-x(1))*x(3)*x(2)];x0=[1,0,0,1]; % 初值xd0=[1,2,3,-5]; % 无需给出确定值，但要判断正负x0f=[1 1 1 1]; % 保留x0xd0f=[]; % 重新计算xd[x0,xd0]=decic(f,0,x0,x0f,xd0,xd0f)% decic为ode15i计算一致的初始条件% t0=0% 求出相容的初值,由x0确定x0'[t,x]=ode15i(f,[0,2],x0,xd0);plot(t,x) % 绘制时间响应曲线

运行结果：（同例3.2）

x0 = 1 0 0 1
xd0 = -0.0000 1.6833 1.0000 -0.5166

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

微分代数方程求解

微分代数方程：指在微分方程中，某些变量间满足满足某些代数方程的约束。

常用求解器：ode15s()、ode45()

微分方程更一般的形式可以写成

M(t,x)*x'=f(t,x)

对于真正的微分代数方程，M(t,x)为奇异矩阵

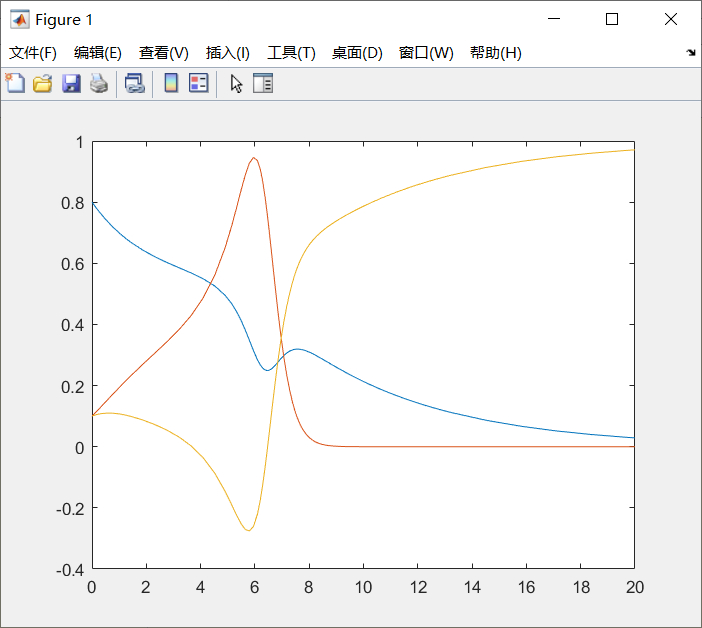
例4.1 考虑下面微分代数方程

x'1=-0.2*x1+x2*x3+0.3*x1*x2
x'2=2*x1*x2-5*x2*x3-2*x2*x2
0=x1+x2+x3-1

初始条件：x1(0)=0.8,x2(0)=x3(0)=0.1

解：用矩阵形式表示该微分代数方程

[1 0 0;0 1 0;0 0 0]*[x'1 x'2 x'3]=[-0.2*x1+x2*x3+0.3*x1*x2;2*x1*x2-5*x2*x3-2*x2*x2;x1+x2+x3-1]

代码如下：

%% 微分代数方程求解f=@(t,x)[-0.2*x(1)+x(2)*x(3)+0.3*x(1)*x(2);
2*x(1)*x(2)-5*x(2)*x(3)-2*x(2)*x(2);
x(1)+x(2)+x(3)-1];M=[1,0,0;0,1,0;0,0,0]; % 输入质量矩阵options=odeset;options.Mass=M; % 设置质量矩阵x0=[0.8;0.1;0.1];[t,x]=ode15s(f,[0,20],x0,options);plot(t,x)% 也可以转换成常微分方程求解fDae=@(t,x)[-0.2*x(1)+x(2)*(1-x(1)-x(2))+0.3*x(1)*x(2);
2*x(1)*x(2)-5*x(2)*(1-x(1)-x(2))-2*x(2)*x(2)]; % 方程右侧的形式模型x0=[0.8,0.1]; % 初值[t,x]=ode45(fDae,[0,20],x0);x3=1-x(:,1)-x(:,2);figure;plot(t,x,t,x3);% 也可以用隐式微分方程求解的方法求解f=@(t,x,xd)[xd(1)+0.2*x(1)-x(2)*x(3)-0.3*x(1)*x(2);
xd(2)-2*x(1)*x(2)+5*x(2)*x(3)+2*x(2)*x(2);
x(1)+x(2)+x(3)-1]; % 隐式微分方程x0=[0.8,0.1,2];x0f=[1,1,0];xd0=[1,1,1];xd0f=[];[x0,xd0]=decic(f,0,x0,x0f,xd0,xd0f); % 相容初始条件% 隐式微分方程求解与绘图res=ode15i(f,[0,20],x0,xd0);% res为struct结构体数组plot(res.x,res.y)

运行结果：

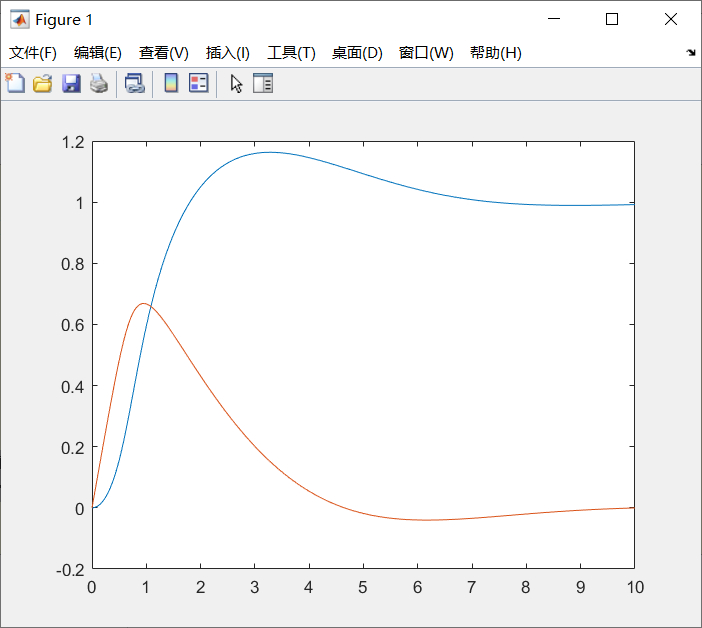
watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16

例4.2 （例3.1）给定隐式微分方程组，已知x1(0)=x2(0)=0，求数值解。

x'1*sin(x1)+x'2*cos(x2)+x1=1
-x'1*cos(x2)+x'2*sin(x1)+x2=0

代码如下：

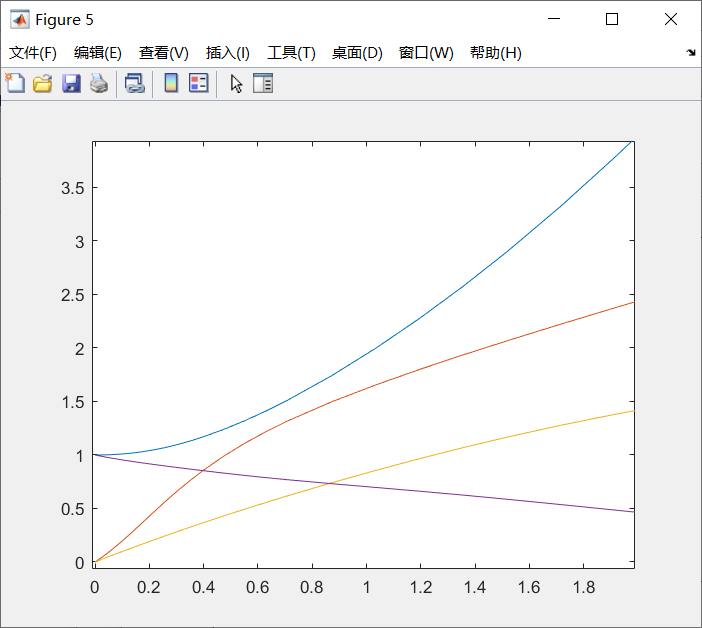
f=@(t,x)[1-x(1);-x(2)];M=@(t,x)[sin(x(1)),cos(x(2));-cos(x(2)),sin(x(1))]; % 质量矩阵options=odeset;options.Mass=M;options.RelTol=1e-6; % 设置求解精度[t,x]=ode45(f,[0,10],[0;0],options);plot(t,x)

运行结果：

watermark,type_d3f5lxplbmhlaq,shadow_50,text_q1netiba5rex5rw35rex5asc5rex,size_20,color_ffffff,t_70,g_se,x_16