一 down-samplig 和up-sampling 介绍

参考：
https://www.cnblogs.com/jngwl/articles/image_sampling.html
https://www.cnblogs.com/jokerjason/p/9429452.html

二 图像语义分割中的上采样(subsampling)和下采样(Upsampling)

参考：
https://blog.csdn.net/qq_37344125/article/details/108717647
https://www.malaoshi.top/show_1EF52HM7gu6g.html
https://blog.csdn.net/laizi_laizi/article/details/103122771
https://jishuin.proginn.com/p/763bfbd2aecd

1下采样（subsampled）

实际上就是卷积层之间的池化操作，本质上也是卷积，只是卷积核没有参数，不带参数的卷积。

2上采样（upsampled）

上采样（upsampling），主要目的是放大原图像
对图像的放大操作不能带来更多关于该图像的信息, 因此图像的质量将不可避免地受到影响。
但使用一些算法可以增加图像的信息，从而使得缩放后的图像质量超过原图质量的。

常用的上采样方法有两种：插值法 (Interpolation，一般是双线性插值）和反卷积 (Deconvolution)，反池化 (unPooling)。

2.1 关于插值的说明：

参考：
https://zhuanlan.zhihu.com/p/111072616

简单来说，插值指利用已知的点来“猜”未知的点，图像领域插值常用在修改图像尺寸的过程，由旧的图像矩阵中的点计算新图像矩阵中的点并插入，不同的计算过程就是不同的插值算法。

常用的插值算法有很多

• 最邻近插值（Nearest Neighbour Interpolation）：计算速度最快，但是效果最差
• 双线性插值（Bilinear Interpolation）：双线性插值是用原图像中4(2*2)个点计算新图像中1个点，效果略逊于双三次插值，速度比双三次插值快，属于一种平衡美，在很多框架中属于默认算法
• 双三次插值算法（Bicubic Interpolation）：双三次插值是用原图像中16(4*4)个点计算新图像中1个点，效果比较好，但是计算代价过大
• 双线性插值的改进算法

最近邻法(Nearest Interpolation)


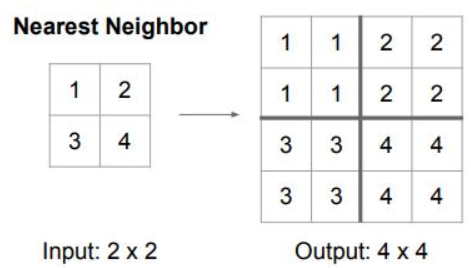
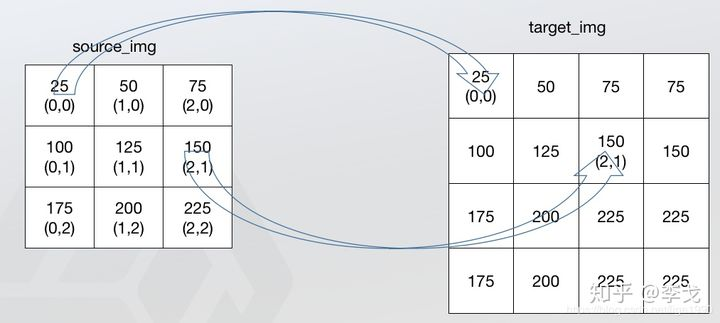
上图效果是最近邻法的计算过程示意图，由上图可见，最近邻法不需要计算只需要寻找原图中对应的点，所以最近邻法速度最快，但是会破坏原图像中像素的渐变关系，原图像中的像素点的值是渐变的，但是在新图像中局部破坏了这种渐变关系。

双线性插值是目前在 语义分割 中用的比较多的一种方式。在这里仅介绍线性插值，重点是双线性插值。

2.2 线性插值

参考：
https://zhuanlan.zhihu.com/p/59244589

在原有图像像素的基础上，在像素点之间采用合适的插值算法插入新的元素。
插值就是在不生成像素的情况下增加图像像素大小的一种方法，在周围像素色彩的基础上用数学公式计算丢失像素的色彩（也有的有些相机使用插值，人为地增加图像的分辨率）。
所以在放大图像时，图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。

线性插值有一阶、二阶、三阶，对应为单线性插值、双线性插值和三线性插值。三者皆为线性插值。三者不同之处在于：

• 单线性插值对应两点之间任意一点为插值；
• 双线性插值对应4点形成方形之间的任意一点作为插值；
• 三线性插值对应8点形成立方体内的任意一点作为插值。

理解了单线性插值，双线性插值和三线性插值则是4点或8点内建立基于单线性插值的桥接，所以，双线性插值需要计算3次线性插值，三线性插值需要计算7次线性插值。双线性插值是目前在 语义分割 中用的比较多的一种方式，算法复杂、计算量大、但极大地消除了锯齿现象。

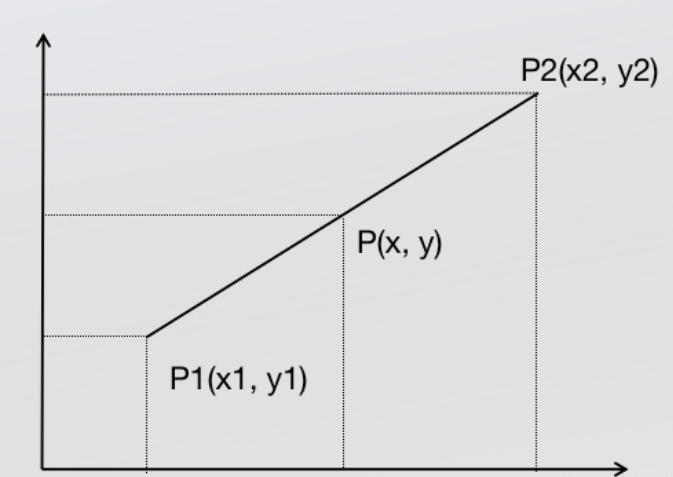
单线性插值

• 1 在一条线上(一维),坐标就是x(用一个值就可以在一条直线上标明位置)，一个坐标对应一个值，就是y
  

双线性插值

参考：https://zhuanlan.zhihu.com/p/111072616

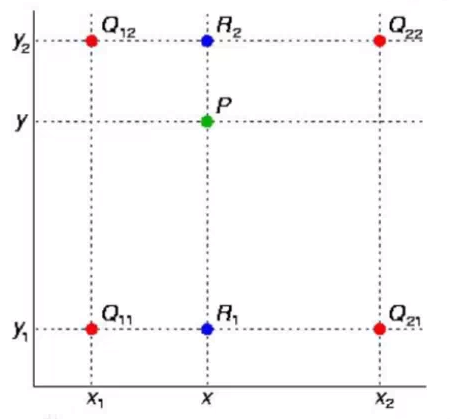
• 1 在一个平面/一个区域(二维),坐标就是(x,y) (必须用两个值/或者说两个方向 才能标明一个平面上的位置)，一个坐标对应一个值，就是z
• 2 实际上就是先进行了 2 次横向的单线性插值，然后根据单线性插值的结果进行 1 次纵向的单线性插值。
  
  
  固定 y,计算不同x对应的值。即：y不变，x变，问题变为：在一条直线上计算单线性插值。
  
  固定 x,计算不同y对应的值。即：x不变，y变，问题变为：在一条直线上计算单线性插值。
  
• 3 双线性插值举例
  
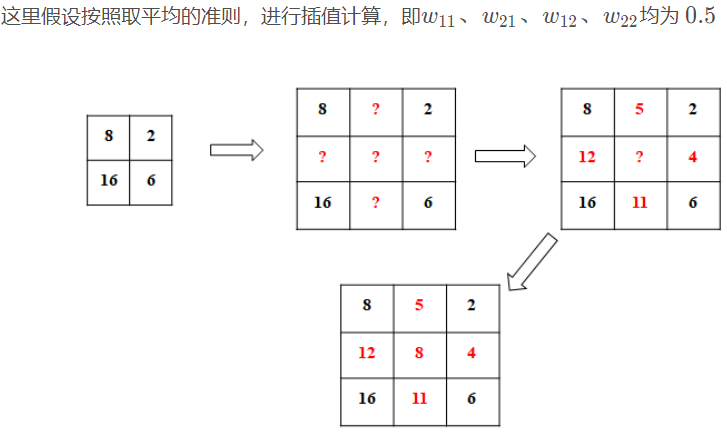
• 4 双线性插值对应关系
  双线性插值的对应公式和前面的最近邻法一样，不一样的是根据对应关系不再是找最近的1个点，而是找最近的4个点，如下图所示。
  
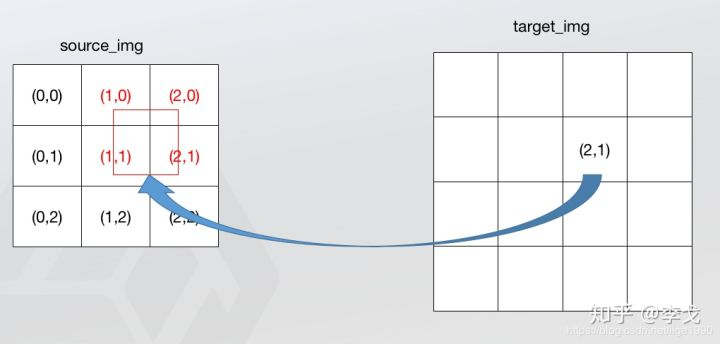
  问题：如果根据对应关系找到原图中的点不是在不同的点之间，而是跟原图像中的点重合，那该如何找4个点？关于这个问题要看一下双线性插值的计算公式，双线性插值实际上是从2个方向一共进行了3次单线性插值，咱们先了解单线性插值的计算方式。
  解答：根据公式可以发现，无论我们怎么选取，其实其余3点的权重都至少1项为0，所以不论我们怎么取剩下的3个点，对最终的结果都不会产生影响。
• 5 双线性插值的优化

参考：https://zhuanlan.zhihu.com/p/111072616

三线性插值

在一个三维空间,坐标就是(x,y，z) (必须用三个值/或者说三个方向 才能标明一个空间中的位置)，一个坐标对应一个值。

插值法总结

在原有图像像素的基础上，在像素点之间采用合适的插值算法插入新的元素。
插值就是在不生成像素的情况下增加图像像素数量的一种方法，在周围像素色彩的基础上用数学公式计算丢失像素的色彩。
所以在放大图像时，图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。

插值方法，我们在决定网络架构的的时候我们需要去选择一种。这有点像人工的特征工程（feature engineering），并且这个过程中网络没有可以学习的。
如果我们想要我们的网络学习怎样最优地进行上采样，我们能够使用转置卷积（transposed convolution）。它不使用预先定义的插值方法，它有可学习的参数。

2.2 转置卷积(Transposed Convolution)/反卷积(Deconvolution)

论文：A guide to convolution arithmetic for deep learning
参考：
1：https://jishuin.proginn.com/p/763bfbd2aecd
2：https://blog.csdn.net/laizi_laizi/article/details/103122771
以上两篇文章都是翻译自：Up-sampling with Transposed Convolution——https://naokishibuya.medium.com/up-sampling-with-transposed-convolution-9ae4f2df52d0
重点看1：https://jishuin.proginn.com/p/763bfbd2aecd

转置卷积也被称作：部分跨越卷积（fractionally strided convolution）或反卷积（deconvolution）

转置卷积操作构建了和普通的卷积操作一样的连接关系，只不过这个是从反向方向开始连接的。我们可以用它进行上采样。另外，这个转置卷积矩阵的参数是可以学习的，因此我们不需要一些人为预先定义的方法。即使它被称为转置卷积，它并不是意味着我们将一些现存的卷积矩阵简单转置并且使用其转置后的值。
从本质来说，转置卷积不是一个卷积，但是我们可以将其看成卷积，并且当成卷积这样去用。
我们通过在输入矩阵中的元素之间插入0进行补充，从而实现尺寸上采样，然后通过普通的卷积操作就可以产生和转置卷积相同的效果了。你在一些文章中将会发现他们都是这样解释转置卷积的，但是这个因为在卷积操作之前需要通过添加0进行上采样，因此是比较低效率的。

上图中的描述来自于论文：A guide to convolution arithmetic for deep learning

论文中区分了转置卷积和用直接卷积来模拟转置卷积(也叫等效的直接卷积),而且论文中描述转置卷积时也都是用用直接卷积来模拟转置卷积(也叫等效的直接卷积)来分析和可视化的。
同时论文中也提到了转置卷积用于与正常卷积做相反方向变换的情况， 即从具有某种卷积输出形状到具有其输入形状的情况，同时保持与所述卷积兼容的连接模式。如下：

因而可以这样理解，代码实现的时候用的是转置卷积，而我们在分析和可视化时候使用**用直接卷积来模拟转置卷积(也叫等效的直接卷积)**更方便，后者也算是转置卷积。

2.3 反池化（unpooling）

出自2013年纽约大学Matthew D. Zeiler和Rob Fergus发表的《Visualizing and Understanding Convolutional Networks》
参考：https://www.malaoshi.top/show_1EF52HM7gu6g.html

在池化过程中，记录下max-pooling在对应kernel中的坐标，在反池化过程中，将一个元素根据kernel进行放大，根据之前的坐标将元素填写进去，其他位置补0。

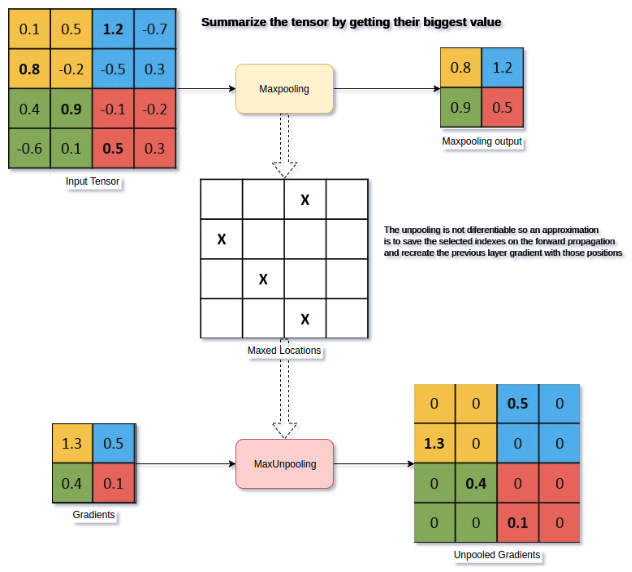
注意：
上图：左下角的图，是右上角的图进行梯度计算后的结果
在CNN中常用来表示max pooling的逆操作。
在SegNet神经网络中用到

3 FCN (Fully Convolutional Networks)

参考：
https://zhuanlan.zhihu.com/p/31428783
https://zhuanlan.zhihu.com/p/22976342
https://zhuanlan.zhihu.com/p/34453588

最后

以上就是稳重豌豆为你收集整理的图像的down-samplig 和up-sampling一 down-samplig 和up-sampling 介绍二 图像语义分割中的上采样(subsampling)和下采样(Upsampling)的全部内容，希望文章能够帮你解决图像的down-samplig 和up-sampling一 down-samplig 和up-sampling 介绍二 图像语义分割中的上采样(subsampling)和下采样(Upsampling)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。