【写在前面:因为之前对这个坐标系的转换理解的很含糊,所以在到posenet的时候,理解起来比较费劲,所以回头又在学习这部分的资料,希望这次能够有个正确的认识,如果有不对的地方,欢迎大家指正,如果有感兴趣的小伙伴,也非常欢迎一起交流,学习】
个人觉得这部分可以分成两部分,
1.世界坐标系->相机坐标系->图像坐标系->像素坐标系
2.像素坐标系->图像坐标系->相机坐标系->世界坐标系
这两类已经涵盖了所有转化的情况,废话少说,开始吧~
1.世界坐标系->相机坐标系->图像坐标系->像素坐标系
- 世界坐标系->相机坐标系
试想一下,我在3D世界中有一个点
那么相机的初始位置,是以相机为坐标原点。试想一下,如果将一个相机放在我们认为的世界坐标系的原点上,其实这个时候相机坐标==世界坐标,但是实际情况下,很少这样的情况发生,那么我们的相机无论多远,我们会相当于世界坐标系的原点,有个平移向量,这个我们可以记为
那么有意思的事情来了,就是其实我的相机坐标,可以通过用一定的
接下来,我们再想想,
旋转矩阵(英语:Rotation matrix)是在乘以一个向量的时候有改变向量的方向但不改变大小的效果并保持了手性的矩阵。旋转矩阵不包括点反演,点反演可以改变手性,也就是把右手坐标系改变成左手坐标系或反之。所有旋转加上反演形成了正交矩阵的集合。旋转可分为主动旋转与被动旋转。主动旋转是指将向量逆时针围绕旋转轴所做出的旋转。被动旋转是对坐标轴本身进行的逆时针旋转,它相当于主动旋转的逆操作。
举个例子,如果沿着z轴旋转,那么其实三维坐标点的z值是不会变的,唯一改变的是x和y方向的值。
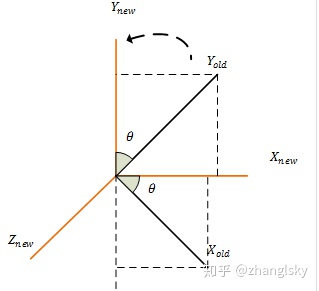
这样我们就得到了,沿着
同理可得,沿着x轴和沿着y轴旋转的变化分别如下:
于是,新的相机坐标,即同时沿着
于是,世界坐标系到相机坐标系的转化可以写成:
- 相机坐标系->图像坐标系(平面坐标系)
刚才,在世界坐标系->相机坐标系的转化过程中,我们知道,通过相机外部的旋转和平移变化,可以和世界坐标系建立一种关联,使两者可以互相转化。
那么在相机坐标系->图像坐标系这个转换过程,跟哪些因素有关呢?试想一下,两个不同的相机,即使在所处的位置一样的情况下,拍摄的两张照片,很大概率是不一样的。那么在此次转化过程中,一定离不开相机自身的一些相关的参数。但是跟相机相关的参数有很多,哪些参数能够为这次转化提供帮助呢,我们需要先了解相机成像的原理,来张经典的图
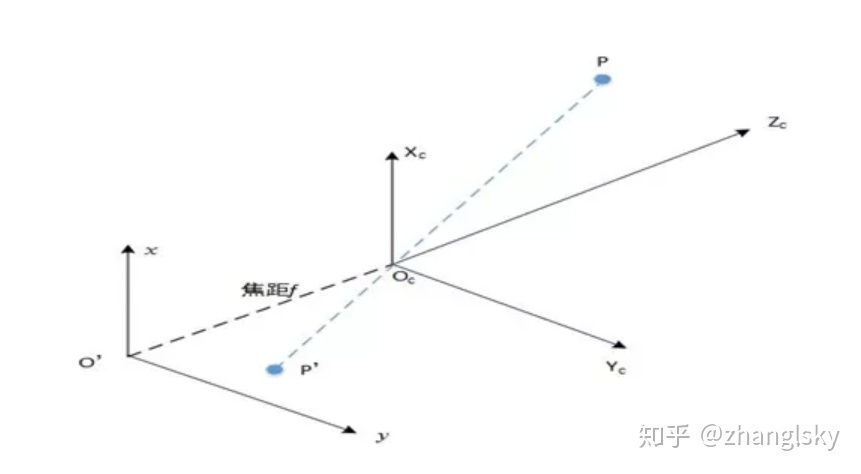
为了方便计算,我们把小孔成像模型对称翻转过来,得到如下的图:
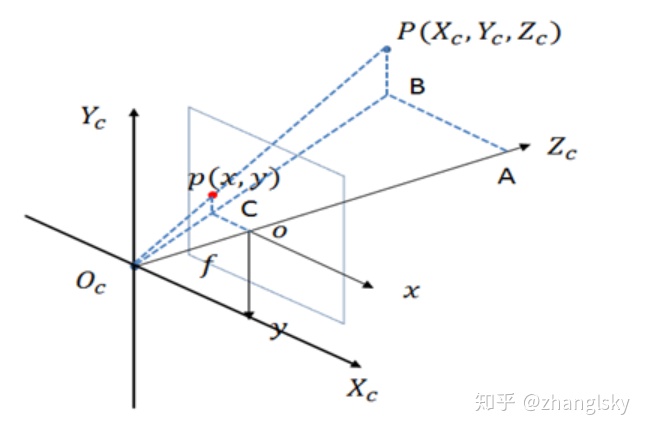
从图像上,如果相机坐标系到图像坐标系的转化,我们可以理解为,如何将相机坐标系下的3D点
同理可得:
然后用矩阵形式,可以得到:
图像坐标系->像素坐标系
当我们拿到了图像坐标系的数据,我们这个时候想把其转换成像素坐标系,如下图:
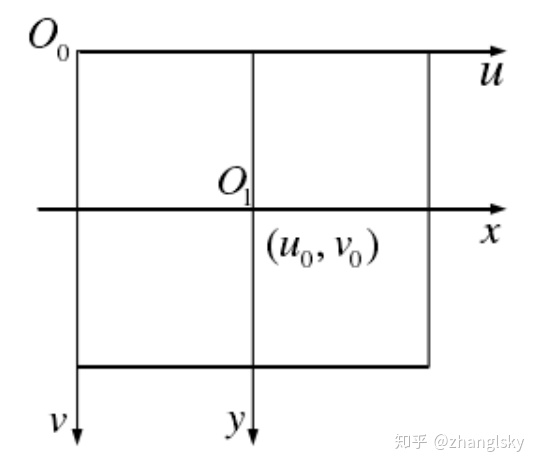
那我们关心几个参数,首先是
于是有
其实在大多数时候,直接是像素坐标系和相机坐标系之间进行转换,因此可以将这两部分的转化矩阵合并,从而得到:
这样我们就完成了从世界坐标系到相机坐标系的一个转换,如果将
其中
2.像素坐标系->图像坐标系->相机坐标系->世界坐标系
参考链接:
林青春:机器视觉几何坐标概论
http://www.cse.psu.edu/~rtc12/CSE486/lecture12.pdf
https://zh.wikipedia.org/wiki/%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5
欧式空间的旋转表示(三)-旋转矩阵
魏川:深入理解旋转矩阵和平移向量的本质
林青春:机器视觉几何坐标概论
为什么要相机标定?你想知道的都在这!_坐标系
最后
以上就是细心灰狼最近收集整理的关于canvas坐标转换屏幕坐标_世界坐标系,相机坐标系,图像坐标系,像素坐标系的转换...的全部内容,更多相关canvas坐标转换屏幕坐标_世界坐标系,相机坐标系,图像坐标系,像素坐标系内容请搜索靠谱客的其他文章。








发表评论 取消回复