Pure Pursuit（纯追踪算法）ROS实践Pure Pursuit（纯追踪算法）ROS实践

75 阅读 0 评论 50 点赞

我是靠谱客的博主隐形大侠，最近开发中收集的这篇文章主要介绍Pure Pursuit（纯追踪算法）ROS实践Pure Pursuit（纯追踪算法）ROS实践，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Pure Pursuit（纯追踪算法）ROS实践

一、背景知识

自主移动机器人，或者说无人驾驶车辆，一般有三大子系统

环境感知子系统（Perception）

无人驾驶车辆通过传感器来获取环境信息，主要包括环境感知、建图、定位等。
行为决策子系统（Planning）

结合导航目标、环境信息、交通规则等信息规划出一条精密的行驶轨迹，无人车沿着这条轨迹移动就能到达终点。
运动控制子系统（Control）

结合行为决策子系统规划的轨迹和车辆当前状态，位置、姿态和速度等，得出无人车的控制量，油门、档位、转向等。

二、Pure Pursuit算法

首先感性的去认识一下纯追踪算法，简单理解就是，无人车关注轨迹中某个点目标goal，然后去追踪它。

在无人地面载具（UGV）场景下，这里的goal是Planning子系统所规划轨迹上的一些点，称为路点（Way Points）。如果轨迹是连续的，就在轨迹上采样多个点。如果轨迹是离散的，那么就可以直接使用。

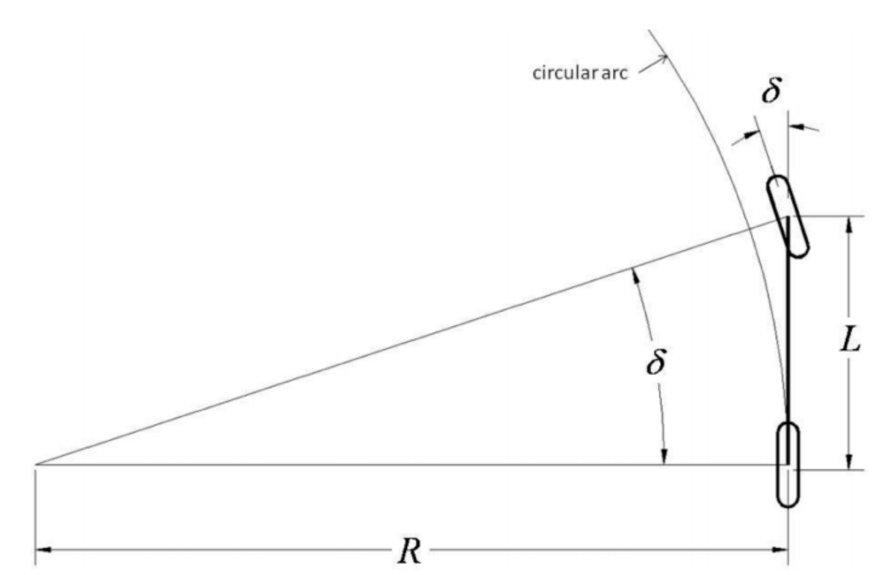
自行车模型

上图是一个自行车模型，接下来简单说明是怎么绘制的。车辆坐标原点在后轴中心，如果转向角δ确定以后，车辆会以某个圆心做一个转圈动作，这个圆的半径就是R。那么pure pursuit算法就是一个横向控制器，通过计算转向角δ来控制车辆，使得车辆后轴中心能沿着轨迹移动。

各变量含义如下：
$delta：前轮的转向角（度）\ & L：轴距（米）\ & R：给定转向角后，车后轴中心遵循的圆的半径 end{aligned}$
根据图中关系可得
$t a n ( δ ) = L R (1) tan(delta)= frac{L}{R} tag{1}$
（1）式的δ是我们要求的转向角，而未知量式R。由于曲率k与半径R呈倒数关系可将（1）式改写为
$tan^{-1}(kL) tag{2}$
这时求解δ就成为了，解等式右边式子，其中L已知，是车辆的轴距，未知量是曲率k。接下来我们就来求解这个k。

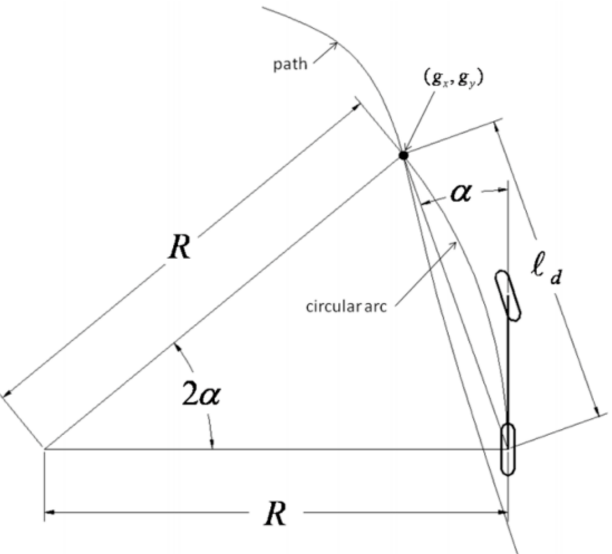
pure pursuit算法几何模型

上图便是pure pursuit算法的几何图形，简单说明一下怎么绘制的。其中点g是我们的目标路点，我们要确定转向角δ（注意，不是图中的α），使后轴中心遵循的圆弧能经过g。再次强调，我们要求是圆弧的半径R，或者说曲率k，上图中的未知量只有R

各变量含义如下
$(g_x,g_y)：目标路点g在车辆坐标系中的位置（即GPS路径中采样的轨迹点）。\ & α：车后轴与目标路点g连成向量与车偏航角夹角。\ & l_d：前视距离。 end{aligned}$
接下来推导怎么求曲率k
在这里插入图片描述

考虑时间t，可以将（2）式表示为
$tan^{-1}(k(t)L) = tan^{-1}(frac{2Lsin(alpha(t))}{l_d}) tag{6}$
至此，pure pursuit算法就变成了每一个时刻求解α。

三、基于GPS定位在ROS上实现

实验平台使用的GPS+惯导套件能提供8位小数精度的定位和偏航角。实验流程是先记录下人工控制移动的GPS轨迹，然后让无人车利用pure pursuit算法去跟随该轨迹移动。

在实现过程中有几个问题需要注意：

根据两个GPS坐标计算距离

如何计算两个GPS点的距离，因为原始算法是以车辆坐标系（笛卡尔坐标系，单位是米）定位每个点的，所以可以直接用欧几里得距离公式求距离，而GPS坐标不是以车辆坐标系定位点，要用到专门的算法求距离。

我们要找到目标路点g，算法过程如下：

（1）找到轨迹上离车后轴中心最近的路点o。

（2）以o为起始位置，遍历之后的路点，将相邻两个路点比如第i，i+1两个点的距离累加到L，直到累加距离L大于前视距离Ld，即找到目标路点g。

刚开始我尝试用近似的方法求解，但是因为距离较小，近似求解误差很大，需要做到很精确的算法，代码网上能查到就不放了。
根据两个GPS坐标计算航向角

计算α角时需要计算从车当前后轴中心坐标到目标路点g的偏航角（相对真北的角度）。同上面的问题一样也是因为原始代码是用的车辆坐标系（笛卡尔坐标系），可以用三角函数求得偏航角。而GPS坐标求解不能用三角函数求解，这时也需要求精确的值，代码网上能查到就不放了。
弧度与角度的转换

数学库里面三角函数sin，cos，tan，atan等函数都是使用的弧度计算，在GPS计算和车辆控制都是用角度计算，在实现pure pursuit算法步骤中要注意弧度和角度的转换。