分享一个简单的迭代学习机器人双臂控制（MATLAB）

1 什么是迭代学习控制

迭代学习控制（iterative learning control，简称ILC）由Uchiyama于1978年首先提出，不过因为论文由日文撰写，影响不是很大。1984年，Arimoto等人用英文介绍了该方法。它是指不断重复一个同样轨迹的控制尝试，并以此修正控制律，以得到非常好的控制效果的控制方法。
迭代学习控制的特点是“在重复中学习”，通过反复的迭代修正，达到改善控制效果的目的。迭代学习控制的原理是根据系统前次运行所获得的输出误差信息，在控制过程中不断修正控制输入，随着迭代的进行，逐步改进下一次控制输入，以使控制效果越来越好。迭代学习控制仅需要较少的先验知识，对于处理模型未知且具有重复运动性质的系统，是一种行之有效的控制策略。

迭代学习的控制律用最简单的表述方式就是：

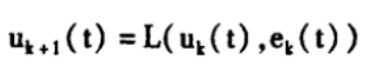
解释一下这几个变量的意义：
—— 第k+1次控制时的控制器在t时刻的输出
—— 第k次控制时控制器在t时刻的输出
—— 第k次控制时参考输出和实际输出的误差
这里L算式可以是任意算法。常用的是P算法、PD算法或PID算法。按照误差更新方式又分为开环迭代和闭环迭代。
以下是一个PD开环迭代学习跟踪机械臂运动程序：
实现轨迹完全跟踪

```MATLAB
clear all;
close all;
m=20;
n=100;
gama=0.9;
x1(1:m,1:n)=0;
x2(1:m,1:n)=0;
u(1:m,1:n)=0;
y(1:m,1:n)=0;
e(1:m,1:n)=0;
err(1:m,1:n)=0;
% b=beronulli(1,1000,1);
% w=randn(m,n)/5;
for n=1:100
y_d(n) = sin(8*(n-1)/50);
%y_d(n) = 5*sin(n*pi/100)+0.3*cos(n*pi/100);
%
if n<=300
%
y_d(n) =5*(-1).^round(n/100);
%
else if n<=700
%
y_d(n) = 5*sin(n*pi/100)+0.3*cos(n*pi/100);
%
else
%
y_d(n) =5*(-1).^round(n/100);
%
end
%
end
%y_d(n)=12*n.^2*(n-1);
%y_d(n) = sin(2*pi*n/50);
end
for k=1:m
for t=2:n-1
x1(k,t)=(-0.8*x1(k,t-1))-0.22*x2(k,t-1)+0.5*u(k,t-1);
x2(k,t)=x1(k,t-1)+u(k,t-1);
y(k,t-1)=(x1(k,t-1)+0.5*x2(k,t-1));
e(k,t-1)=y_d(t-1)-y(k,t-1);
err(k,t-1)=abs(e(k,t-1)).^2;
end
for t=2:n-1
u(k+1,t-1)=u(k,t-1)+gama*e(k,t)+0.3*e(k,t-1);
end
errn(k)=max(err(k,:));
end
plot(y_d(1:90),'-r');hold on
plot(y(1,1:90));hold on;
plot(y(2,1:90));hold on;
plot(y(3,1:90));hold on;
plot(y(5,1:90));hold on;
% plot(y(8,1:90));hold on;
%plot(y(10,1:90));hold on;
%plot(y(15,1:90));hold on;
figure
plot(err(5,1:90));
%plot(err(12,1:20));hold on
%plot(err(15,1:20));hold on
k=1:20;
figure;plot(k,errn(k))

最后

以上就是花痴鲜花为你收集整理的分享一个简单的迭代学习机器人双臂控制（MATLAB）的全部内容，希望文章能够帮你解决分享一个简单的迭代学习机器人双臂控制（MATLAB）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。