前段时间尝试了C语言实现PSO算法求计算二元函数极值,这几天稍微空闲下来了又想尝试用另一种比PSO难一点的经典智能优化算法解决这个问题。
PSO传送门
遗传算法应用还是非常广泛的。之前打数模的时候经常用它求解公式,或者利用它做一些调度类的问题,例如经典的柔性车间调度问题。但是,在实现的时候更多的是借助matlab和python,有的时候直接拿现成的代码修改参数直接用,对算法的理解还是很不到位的。趁这个机会,打算用C语言实现一次GA算法。
自制的GA算法流程图如下,和PSO算法一样,个人认为这类算法还是静下心来直接看代码比较好理解,效率更高。
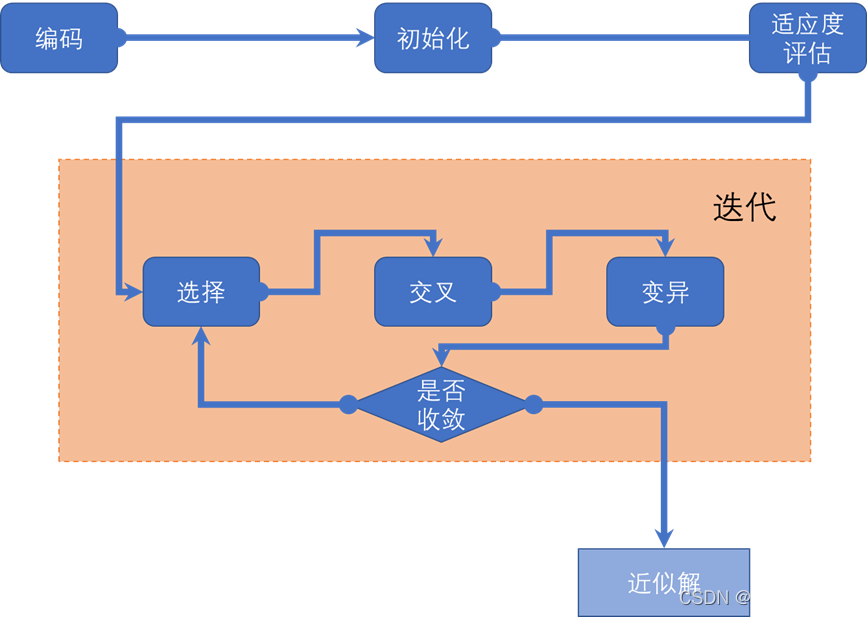
整个算法实际上分为两大部分,第一部分是在为后来的迭代做准备,包括数据编码,初始化等等操作,为第二部分的迭代准备原材料。第二部分是迭代,实际上就是不断地加工第一部分提供的原材料,直到收敛得到最优结果。
实例
待求极值函数如下: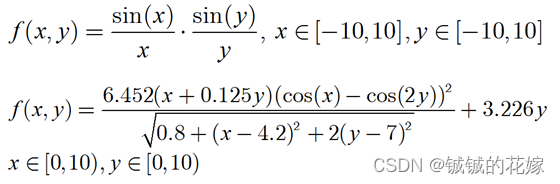
C语言代码如下,主要的流程在genetic函数里写的比较清楚;两个题目可以在fitting函数里面切换,修改的时候记得改#define里的最大最小值。里面的参数需要根据题目自己调整。
#include<bits/stdc++.h>
using namespace std;
// 染色体数量 也就是种群数量
#define chromosome_size 300
// 染色体长度 也就是维度
#define chromosome_length 2
// 进化代数 也就是迭代次数
#define epoch_max 30
// 变量上下界
#define bound_down 0
#define bound_up 10
// 交叉概率
#define cross_probability 0.5
// 变异概率 => 模仿生物学,这玩意要低
#define mutation_probability 0.1
// 染色题本身 二维就是这个解的x,y存储
double chromosome[chromosome_size][chromosome_length];
// 染色体适应度函数 二维就是这个解的x,y对应的函数的值的存储
double chromosome_fitness[chromosome_size];
// 个体被选中的概率,这个是遗传算法的特色
double chromosome_chosen[chromosome_size];
// 每次迭代的最优解
double epoch_best_fitness[epoch_max];
// 每次迭代的最优解的位置,在二维里就是对应的x, y
double epoch_best[epoch_max];
// 之前所有迭代的最优解的平均值
double average_epoch_best_fitness[epoch_max];
// 存储目前所有迭代中的最优解
double all_best_fitness;
// 存储目前所有迭代中的最优解出现的代数
int all_best_epoch;
// 求和函数,因为不让用库,只能手写一个
double sum(double fit[])
{
double sum_fit = 0;
for(int i=0;i<chromosome_length;i++)
sum_fit += fit[i];
return sum_fit;
}
// 计算适应度的函数,在二维的情况下其实就是计算x, y这俩对应的函数的解
double fitting(double fit[]){
// 第一题:
// double fitness = sin(fit[0])/fit[0]+sin(fit[1])/fit[1];
// 第二题
double fitness = (6.452*(fit[0]+0.125*fit[1])*pow((cos(fit[0])-cos(2*fit[1])),2))/sqrt(0.8+pow((fit[0]-4.2),2)+2*pow((fit[1]-7),2))+3.226*fit[1];
return fitness;
}
// 作用其实就是比较所有散点对应的适应度,输出最大的适应度和对应的位置
double* max_in_community(double fit[], int size){
static double result[2];
result[0] = *fit;
result[1] = 0;
for(int i = 0; i < size; i++)
if(fit[i]>result[0]){
result[0] = fit[i];
result[1] = i;
};
return result;
}
// 初始化函数,一开始还是随机初始化
void initialization(void){
for(int i = 0; i < chromosome_size; i++){
for(int j = 0; j < chromosome_length; j++)
// 初始化第一代
chromosome[i][j] = bound_up*(((double)rand())/RAND_MAX)+bound_down;
// 顺便算出来第一批染色体的适应度函数
chromosome_fitness[i] = fitting(chromosome[i]);
}
}
// 选择:求最大值时,适应度越高,被选择的概率越大,经过选择之后,chromosome中大的比例明显提高了
void select(double chromosome[chromosome_size][chromosome_length]){
double fitness_sum = 0;
for(int i=0; i<chromosome_size; i++){
// 计算适应度
chromosome_fitness[i] = fitting(chromosome[i]);
// 求和,为了之后能算概率
fitness_sum += chromosome_fitness[i];
}
// 计算每个染色体的概率
for(int i=0; i<chromosome_size; i++){
if(i==0)
chromosome_chosen[i] = chromosome_fitness[i]/fitness_sum;
else
chromosome_chosen[i] = chromosome_fitness[i]/fitness_sum+chromosome_chosen[i-1];
}
// 选择的主体 => 随机数筛选,染色体的概率越大,越容易被select到
int index[chromosome_size];
for(int i=0; i<chromosome_size; i++){
double rand0 = ((double)rand())/RAND_MAX;
while(rand0<0.0001)
rand0 = ((double)rand())/RAND_MAX;
for(int j=0; j<chromosome_size; j++){
if(rand0<=chromosome_chosen[j]){
index[i] = j;
break;
}
}
}
// 选择完了,在这里记录
for(int i=0;i<chromosome_size;i++){
for(int j=0;j<chromosome_length;j++)
chromosome[i][j]=chromosome[index[i]][j];
chromosome_fitness[i] = chromosome_fitness[index[i]];
}
}
// 交叉
void cross(double chromosome[chromosome_size][chromosome_length]){
for(int i=0;i<chromosome_size;i++){
// 上来先判断是否进行交叉操作,大于交叉概率就跳过
double pick = ((double)rand())/RAND_MAX;
if(pick>cross_probability)
continue;
// 交叉涉及到两个染色体,在这里随机抽取两个染色体,下面两个是两个染色体的编号
int rand1 = (int)((chromosome_size-1)*((double)rand())/RAND_MAX);
int rand2 = (int)((chromosome_size-1)*((double)rand())/RAND_MAX);
// 交叉主体
int flag = 0; // 用来判断后面的循环是否要退出的
while(!flag){
// 看染色体的哪部分拿过来交叉互换
int where = (int)((chromosome_length-1)*((double)rand())/RAND_MAX);
double v1 = chromosome[rand1][where];
double v2 = chromosome[rand2][where];
// rand是指交叉时采用交叉对象的比例
double rand0 = ((double)rand())/RAND_MAX;
chromosome[rand1][where] = rand0*v2 + (1-rand0)*v1;
chromosome[rand2][where] = rand0*v2 + (1-rand0)*v2;
// 判定上下界,在界内就算这次交叉算数,不然重新交叉
if(chromosome[rand1][where]<=bound_up&&chromosome[rand1][where]>=bound_down)
if(chromosome[rand2][where]<=bound_up&&chromosome[rand2][where]>=bound_down)
flag = 1;
}
}
}
// 变异
void mutation(double chromosomes[chromosome_size][chromosome_length]) {
for(int i=0;i<chromosome_size;i++){
// 上来先判断是否进行变异操作,大于变异概率就跳过
double pick = ((double)rand())/RAND_MAX;
if(pick>mutation_probability)
continue;
// 随机抽取染色体的一个位置
int where = (int)((chromosome_length-1)*((double)rand())/RAND_MAX);
double v1 = chromosome[i][where] - bound_up;
double v2 = bound_down - chromosome[i][where];
double r = ((double)rand())/RAND_MAX;
double r1 = ((double)rand())/RAND_MAX;
if(r>=0.5)
chromosome[i][where] = chromosome[i][where] - v1*r1*(1-((double)i)/epoch_max)*(1-((double)i)/epoch_max);
else
chromosome[i][where] = chromosome[i][where] + v1*r1*(1-((double)i)/epoch_max)*(1-((double)i)/epoch_max);
}
}
// 遗传搜索
void genetic(){
//————————————Step1————————————//
//——————————各种初始化——————————//
// 初始化染色体
initialization();
// 该轮所有染色体适应度的最大值和index
double *best_fitness_index;
best_fitness_index = max_in_community(chromosome_fitness, chromosome_size);
// 初始化平均值
average_epoch_best_fitness[0] = sum(chromosome_fitness)/chromosome_size;
// 初始化每代最佳染色体与适应度对应的适应度
all_best_fitness = best_fitness_index[0];
all_best_epoch = 0;
for(int i = 0; i < chromosome_length; i++)
epoch_best[i] = chromosome[(int)best_fitness_index[1]][i];
//————————————Step2————————————//
//————————————迭代————————————//
for(int i=0; i<epoch_max; i++){
// 选择交叉变异一套搞定
select(chromosome);
cross(chromosome);
mutation(chromosome);
//更新一系列数据
// 计算操作后染色体对应的适应度
for(int j=0; j<chromosome_size; j++)
chromosome_fitness[j] = fitting(chromosome[j]);
// 计算平均值
average_epoch_best_fitness[i+1] = sum(chromosome_fitness)/chromosome_size;
// 储存最优表现
best_fitness_index = max_in_community(chromosome_fitness, chromosome_size);
if(best_fitness_index[0] > all_best_fitness){
all_best_fitness = best_fitness_index[0];
for(int k=0; k<chromosome_length; k++)
epoch_best[k] = chromosome[(int)best_fitness_index[1]][k];
all_best_epoch = i+1;
}
printf("第%d次迭代:(%lf,%lf)t%lfn", i, chromosome[(int)best_fitness_index[1]][0], chromosome[(int)best_fitness_index[1]][1], best_fitness_index[0]);
}
}
int main(){
//程序开始和结束时间
clock_t begin, end;
begin = clock(); //开始计时
srand((unsigned)time(NULL)); // 初始化随机数种子
// 搜索
genetic();
end = clock();
printf("计算总耗时:%lf秒n", ((double)(end-begin))/CLOCKS_PER_SEC);
printf("遗传算法进化了%d次,最优值为:%lf,最优值在第%d代取得,此代的平均最优值为%lf.n",epoch_max,all_best_fitness,all_best_epoch,average_epoch_best_fitness[all_best_epoch]);
printf("取得最优值的地方为(%lf,%lf).n",epoch_best[0],epoch_best[1]);
return 0;
}
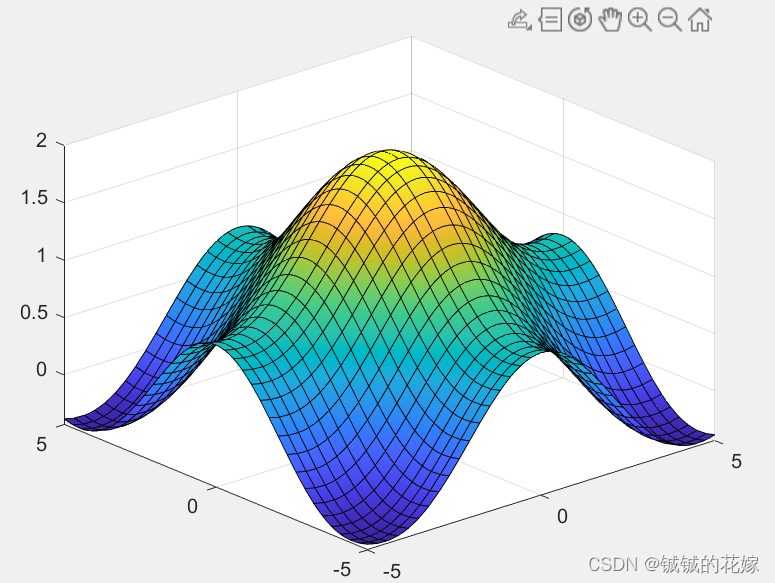
不是很确定最后的结果对不对,拿matlab试试结果。先浅浅画俩图:
fsurf(@(x,y)sin(x)/x+sin(y)/y)
fsurf(@(x,y)(6.452*(x+0.125*y)*(cos(x)-cos(2*y))^2/(0.8+(x-4.2)^2+2*(y-7)^2)^(1/2))+3.226*y)
例题1:
例题2:
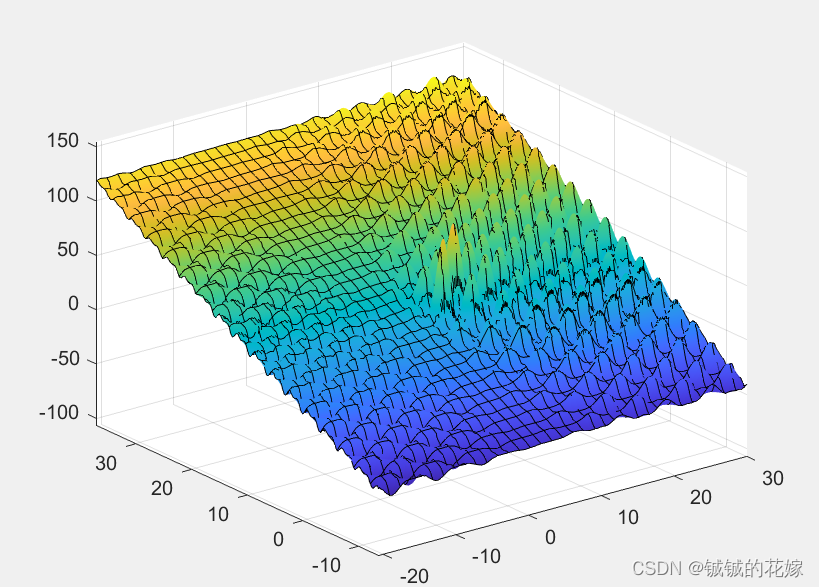
matlab自带PSO求解工具计算极值,因为这个东西只能算最小值,所以对原函数取负号,得到的最小值再取负就是我们要的最大值:
[x,fval] = ga(@(x)-(sin(x(1))/x(1)+sin(x(2))/x(2)),2,[],[],[],[],[-10,-10],[10,10], [], gaoptimset('CrossoverFraction', 0.6))
[x,fval] = ga(@(x)-(6.452*(x(1)+0.125*x(2))*(cos(x(1))-cos(2*x(2)))^2/(0.8+(x(1)-4.2)^2+2*(x(2)-7)^2)^(1/2)+3.226*x(2)),2,[],[],[],[],[0,0],[10,10], [], gaoptimset('CrossoverFraction', 0.6))
运行结果如下:


经过证明,我们C语言的实现是没什么大问题的。
最后
以上就是沉静老鼠最近收集整理的关于遗传算法(GA)计算二元函数极值(C语言实现、matlab工具箱实现)实例的全部内容,更多相关遗传算法(GA)计算二元函数极值(C语言实现、matlab工具箱实现)实例内容请搜索靠谱客的其他文章。








发表评论 取消回复