无模型自适应ILC原理及代码实现
这里学习的是很老的一篇论文《基于无模型自适应控制的反馈-前馈迭代学习控制系统收敛性研究》,作者是晏静文和侯忠生,大家有兴趣可以找来看看。这里主要介绍的无模型自适应的控制率的matlab代码仿真实现和结果分析。
首先数值给出了问题定义,给出m维输入q维输入的非线性系统:
y
n
(
k
+
1
)
=
f
(
u
n
(
k
)
,
y
n
)
(
k
)
,
ξ
(
k
)
,
k
)
y_{n}(k+1)=f(u_{n}(k),y_{n})(k),xi(k),k)
yn(k+1)=f(un(k),yn)(k),ξ(k),k)
两个假设是为了收敛性证明提出的,这里不详细讲(其实收敛性推导我也没推),然后对于该系统设计了前馈和反馈控制律如下:
u
n
(
k
)
=
u
n
f
(
k
)
+
u
k
b
(
k
)
u_{n}(k)=u^{f}_{n}(k)+u^{b}_{k}(k)
un(k)=unf(k)+ukb(k)
u
n
f
(
k
)
=
u
n
−
1
f
(
k
)
+
β
e
n
−
1
(
k
+
1
)
u^{f}_{n}(k)=u^{f}_{n-1}(k)+beta e_{n-1}(k+1)
unf(k)=un−1f(k)+βen−1(k+1)
u
n
b
(
k
)
=
u
n
b
(
k
−
1
)
+
ρ
∗
ϕ
n
(
k
)
λ
+
∣
ϕ
n
^
(
k
)
∣
2
∗
[
y
d
(
k
+
1
)
−
y
n
(
k
)
]
u^{b}_{n}(k)=u^{b}_{n}(k-1)+frac{rho *phi_{n}(k)}{lambda+|hat{phi_{n}}(k)|^{2}}*[y_{d}(k+1)-y_{n}(k)]
unb(k)=unb(k−1)+λ+∣ϕn^(k)∣2ρ∗ϕn(k)∗[yd(k+1)−yn(k)]
ϕ
n
^
(
k
)
=
ϕ
n
^
(
k
−
1
)
+
η
Δ
u
k
−
1
b
μ
+
∣
Δ
u
k
−
1
b
∣
2
∗
[
Δ
y
n
(
k
)
−
ϕ
^
n
(
k
−
1
)
Δ
u
n
b
(
k
−
1
)
]
hat{phi_{n}}(k)=hat{phi_{n}}(k-1)+frac{eta Delta u^{b}_{k-1} }{mu +|Delta u^{b}_{k-1}|^2}*[Delta y_{n}(k)-hatphi_{n}(k-1)Delta u^{b}_{n}(k-1)]
ϕn^(k)=ϕn^(k−1)+μ+∣Δuk−1b∣2ηΔuk−1b∗[Δyn(k)−ϕ^n(k−1)Δunb(k−1)]
ϕ
^
n
(
k
)
=
ϕ
^
(
1
)
,
若
ϕ
^
n
(
k
)
≤
ϵ
或
∣
Δ
u
n
b
(
k
−
1
)
≤
ϵ
∣
hatphi_{n}(k)=hat phi(1), 若hatphi_{n}(k)leqepsilon 或|Delta u^{b}_{n}(k-1)leqepsilon|
ϕ^n(k)=ϕ^(1),若ϕ^n(k)≤ϵ或∣Δunb(k−1)≤ϵ∣
终于把公式打完了,latex真麻烦(对于第一次用的人来说)。可以看到控制部分有两部分组成,前馈和反馈,外加伪偏导迭代公式。
仿真系统如下:
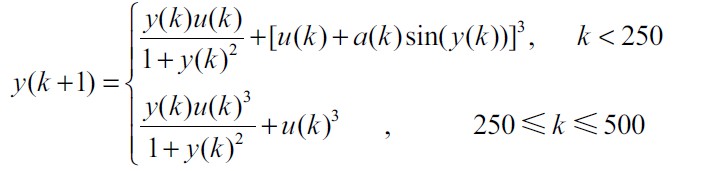
期望曲线:
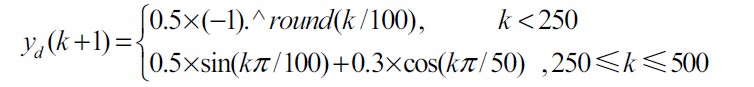
基于控制律和系统编写matlab代码如下:
% 期望轨迹
for k = 1:1:500
if k < 250
yd(k+1) = 0.5*(-1).^(round(k/100));
else
yd(k+1) = 0.5*sin((k*pi)/100) + 0.3*cos((k*pi)/50);
end
end
% 参数设置
epsilon = 0.01;
eta = 1;
rho = 0.2;
lamda = 1;
mu = 2;
% 控制过程
i_n = 60;
%迭代次数
y(1:i_n,1:500) = 0;
for i = 1:1:i_n
for k = 1:1:500
if k == 1
phi(i,k) = 0.4;
elseif k == 2
phi(i,k) = phi(i,k-1) + (eta*(ub(i,k-1) - 0)/(mu + norm(ub(i,k-1) - 0)^2))*(y(i,k) - 0 - phi(i,k-1)*(ub(i,k-1) - 0));
else
phi(i,k) = phi(i,k-1) + (eta*(ub(i,k-1) - ub(i,k-2))/(mu + norm(ub(i,k-1) - ub(i,k-2))^2))*(y(i,k) - y(i,k-1) - phi(i,k-1)*(ub(i,k-1) - ub(i,k-2)));
end
if i == 1
uf(i,k) = 0;
else
uf(i,k) = uf(i-1,k) + 0.4*e(i-1,k+1);
end
if k == 1
ub(i,k) = 0;
else
ub(i,k) = ub(i,k-1) + (rho*phi(i,k)/(lamda + norm(phi(i,k))^2))*(yd(k+1) - y(i,k));
end
if k>2 && (phi(i,k) <= epsilon || (abs(ub(i,k-1) - ub(i,k-2)) <= epsilon))
phi(i,k) = phi(i,1);
end
u(i,k) = uf(i,k) + ub(i,k);
%系统函数
if k <250
y(i,k+1) = y(i,k)*u(i,k)/(1 + norm(y(i,k))^2) + (u(i,k) + 0.1*round(k/500)*sin(y(i,k)))^3;
else
y(i,k+1) = y(i,k)*u(i,k)^3/(1 + norm(y(i,k))^2) + u(i,k)^3;
end
e(i,k+1) = yd(k+1) - y(i,k+1);
end
end
%误差
for i =1:1:i_n
e_min(i) = max(abs(e(i,:)));
end
figure(1)
plot(yd,'r'); hold on;
plot(y(i_n,:),'b'); title('µü´ú10´Î');
figure(2)
plot(e_min);title('error of time k');
代码就是按照控制律来写的,还是自己敲一下印象深刻。
仿真结果:迭代10次结果:
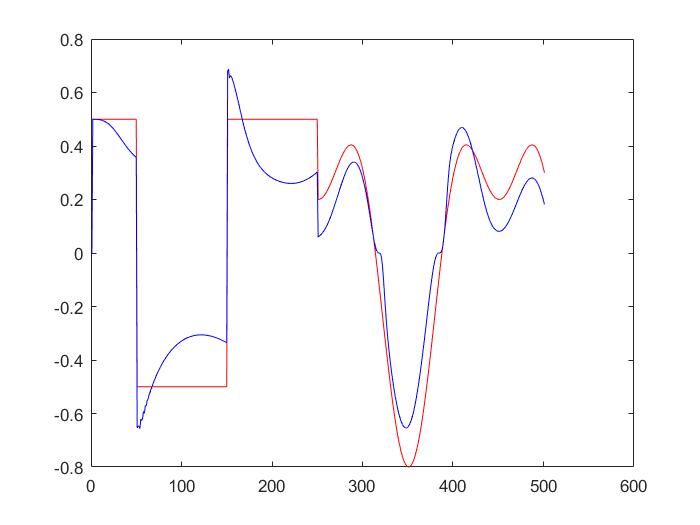
50次迭代:
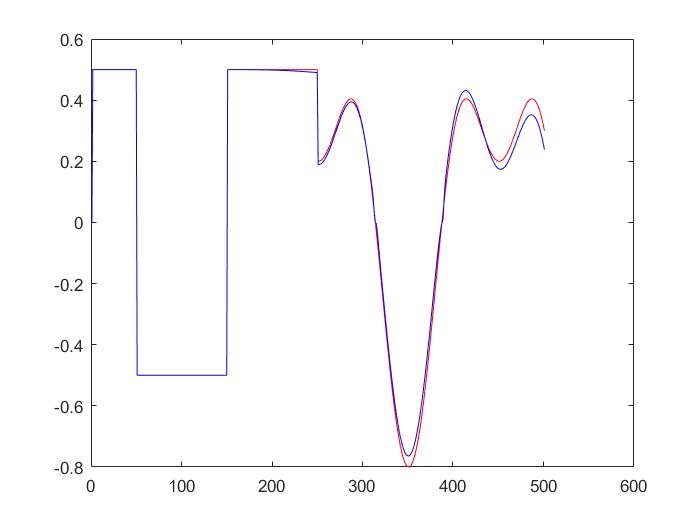
100次迭代:
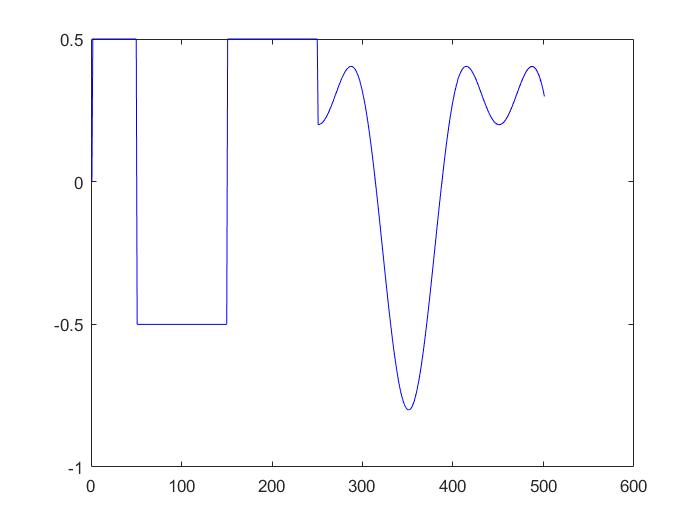
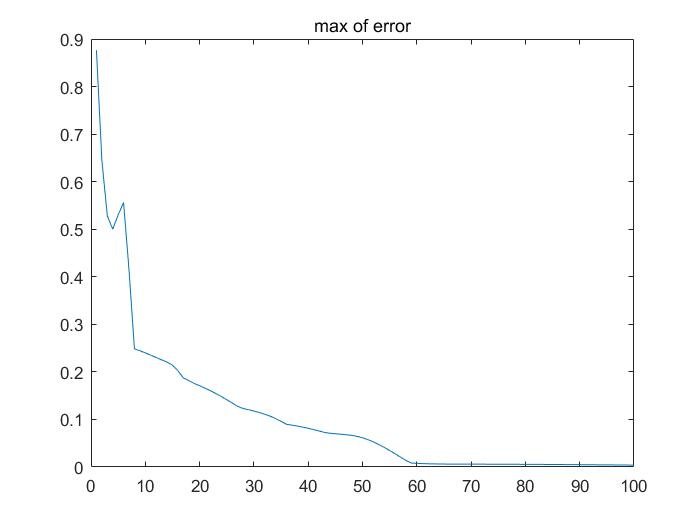
100次迭代 最大误差和最下误差收敛结果:
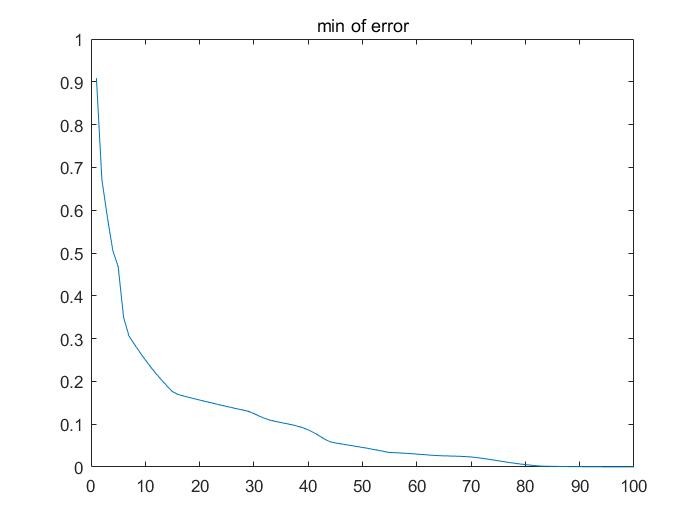
结束。
最后
以上就是懦弱枫叶最近收集整理的关于无模型自适应迭代学习控制原理和matlab代码仿真学习记录的全部内容,更多相关无模型自适应迭代学习控制原理和matlab代码仿真学习记录内容请搜索靠谱客的其他文章。








发表评论 取消回复