用matlab编写了一个DSP数据处理小软件

MyDSP信号处理软件-使用说明书

源程序：
https://pan.baidu.com/s/1mGNITpC_mDnMIF_E59BeAw?pwd=1234
提取码：1234

信号处理软件MyDSP基于Matlab开发，设计了友好的GUI界面，除了处理试验数据外，还可以对仿真数据进行分析，用于故障诊断分析研究。除具有商业软件常规数据处理功能（如平滑、滤波、微分、积分、频谱分析等），还利用最新的数据处理技术，开发了小波分析、希尔伯特变换、EMD分解、VMD分解等功能，可以通过对NVH信号分析来进行故障诊断，另外，数据处理技术也在不断进步中，利用Matlab进行二次开发，可以不断地利用最新的研究成果。
软件的主要功能如下：
(一)GUI界面
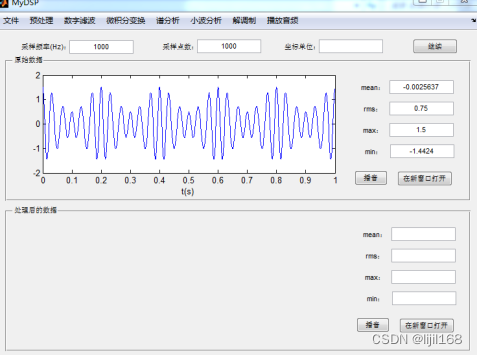
主要由绘图区和菜单组成，绘图区完成试验原始数据图和处理后的数据图的绘制，并会显示信号的采样频率及采样点数，自动统计出信号的均值、有效值、最大值、最小值。

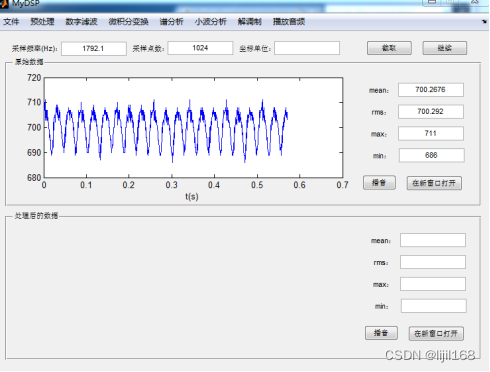
(二)文件
商业软件测试的振动和噪声数据可以导出为txt格式文件，然后用本软件直接读取，录制的音频文件可以直接用本软件打开，仿真的数据可以txt 格式导入到本软件中。
(三)预处理。
预处理包括消除趋势项及平滑，在振动测试中采集到的振动信号数据，由于放大器随温度变化产生的零点漂移、传感器频率范围外低频性能的不稳定以及传感器周围的环境干扰，往往会偏离基线，甚至偏离基线的大小还会随时间变化。偏离基线随时间变化的整个过程被称为信号的趋势项，趋势项直接影响信号的正确性，应该讲其去除。本软件是采用最小二乘法去除趋势项。
通过数据采集器采样得到的振动信号数据往往叠加有噪声信号。噪声信号除了有50Hz的工频及其倍频等周期性的干扰信号外，还有不规则的随机干扰信号。由于随机干扰信号的频带较宽，有时高频成分所占的比例还比较大，使得采集到离散数据绘成的振动曲线上呈现许多毛刺，很不光滑。为了削弱干扰信号的影响，提高振动曲线光滑度，常常需要对采样数据进行平滑处理。本软件采用5点滑动平均法进行数据平滑。
软件操作流程如下：
1、菜单“文件”->“打开”，打开保存试验数据的文本文件，导入数据。

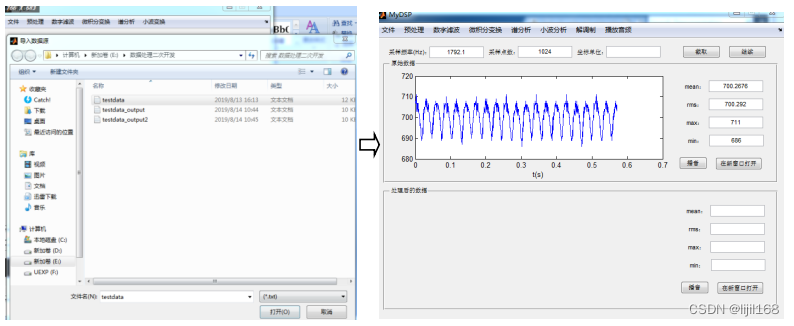
2、菜单“预处理”->“消除趋势项”，打开“输入拟合多项式阶数”对话框，设置拟合多项式阶数，再点击ok按钮，消除趋势项后的数据图在绘图区显示。

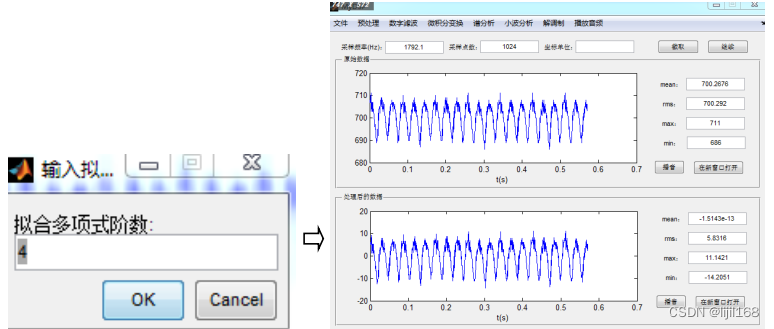
3、菜单“文件”->“另存为”，将处理后数据保存到新的文本文件。
4、菜单“文件”->“打开”，打开刚才保存的经处理试验数据的文本文件，导入数据，然后点击菜单“预处理”->“平滑”，在弹出的对话框中设置平滑方法及平滑的次数，点击OK按钮。

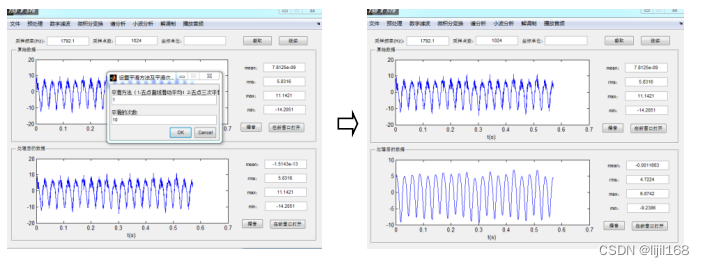
(四)数字滤波。
在振动信号分析中，数字滤波是通过数学运算从所采集的离散信号中选取人们所感兴趣的一部分信号的处理方法。它的主要作用有虑除测试信号中的噪声或虚假成分、提高信噪比、平滑分析数据、抑制干扰信号、分离频率分离等。本软件采用频率滤波法，先对信号进行傅里叶变换，将变换后的频域信号进行修改，然后再经过傅里叶逆变换，得到滤波后的信号。
1、菜单“数字滤波”->“频域低通带通滤波”。

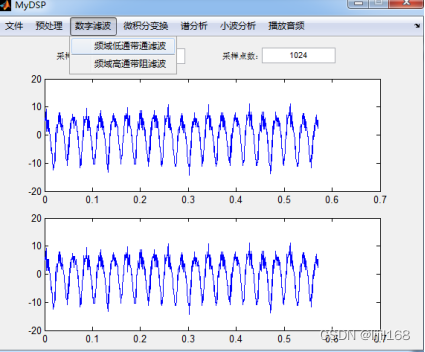
2、设置截止频率，得到滤波后的结果。“频域高通带阻滤波”操作类似。

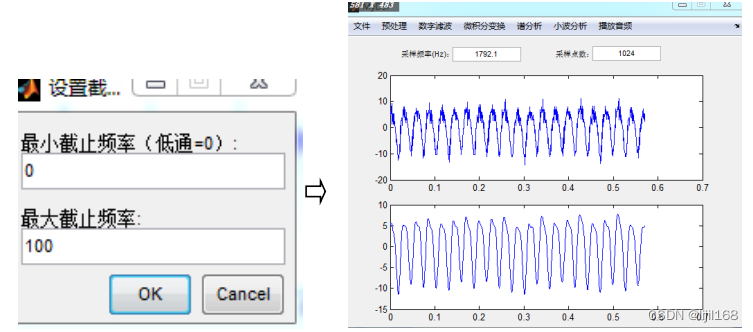
(五)微积分变换。
在振动信号测试过程中，由于仪器设备或测试环境的限制，有的物理量往往需要通过对采集的其他物理量进行转换处理才能得到。例如，将加速度振动信号转换成速度或位移信号。常用的转换处理方法有几分和微分。商业软件采用时域积分算法，结果会带有常数项，本软件采用频域微分和频域微分算法，先将时域信号经过傅里叶变换变成频率信号，然后利用傅里叶变换的微积分性质，求得频域的微分和积分信号，再经傅里叶逆变换得到微分和积分的时域信号，不会出现常数项。
1、菜单“微积分变换”->“频域微积分变换”。

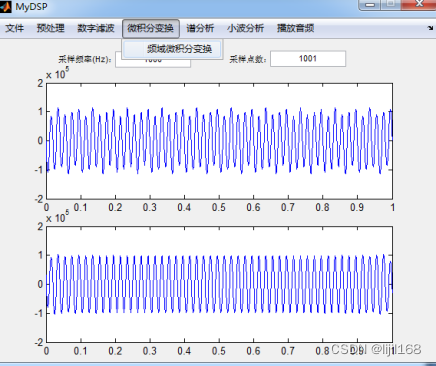
2、设置微积分次数，得到处理后的结果。

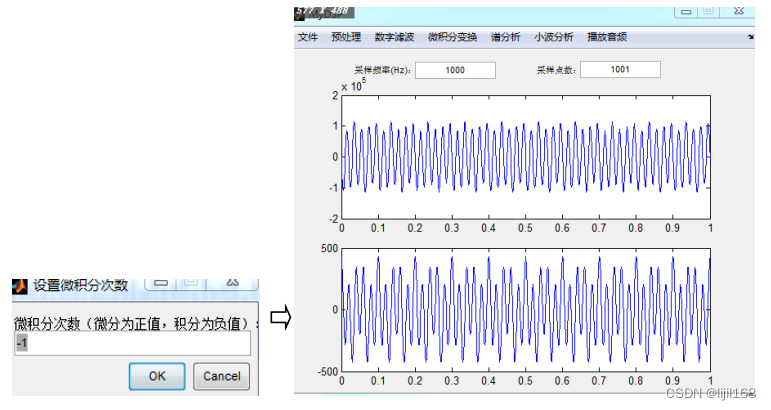
(六)谱分析。
作为时间函数的振动信号，通常在时间域里描述改信号随时间变化的性质。但是在振动信号分析方法中往往还需要采用频率域的概念对信号进行描述，把复杂的振动信号分解为多个不同频率的简谐振动信号。对周期信号可以用傅里叶级数展开法来进行分解，而非周期信号则用傅里叶积分变换来完成，从得到的频谱可以分析出不同频率信号的强弱及分布。由于傅里叶变换对时域信号在整个时域进行积分变换，得到的频谱没有时间量，这对稳态信号是没有问题的。
对瞬态信号而言，不仅需要得到频率信息，还需要得到时间信息，可以考虑对时域信号加窗移窗进行傅里叶变换，这就是短时福利叶变换，可以得到时频谱。短时傅里叶变换的一个主要缺点是其频率分辨率和时间分辨率是固定的，而在自然界，往往高频信号持续的时间短，低频信号持续的时间长，这就需要信号分析时，对高频信号的时间分辨力高，对低频信号的频率分辨率高，小波变换具有这种优势。
与傅里叶变换类似，小波变换将时域信号看成不同频率时间移位的小波函数组合而成，与简谐函数不同，小波函数还有时间自变量，所以小波变换可以得到时频谱。自然界很多信号适合用小波变换进行分析，而我们的眼睛和耳朵则是天然的小波滤波器。小波变换在降噪、故障诊断中有广泛的运用。
商业软件自带小波基函数较少，本软件可充分利用Matlab自带的大量小波基函数，并可以自定义小波基函数，提高了信号处理的能力。
1、菜单“谱分析”->“频域”。得到FFT计算的幅度谱和相位谱。

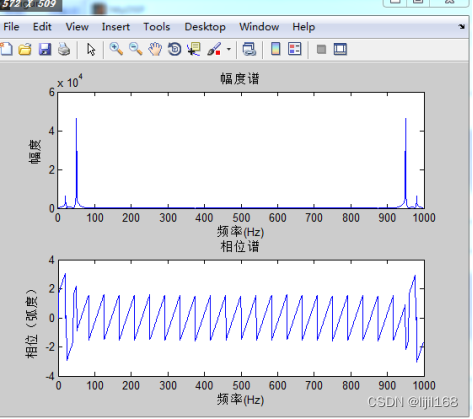
2、菜单“谱分析”->“倒频谱”，得到FFT-IFFT计算的倒频谱。

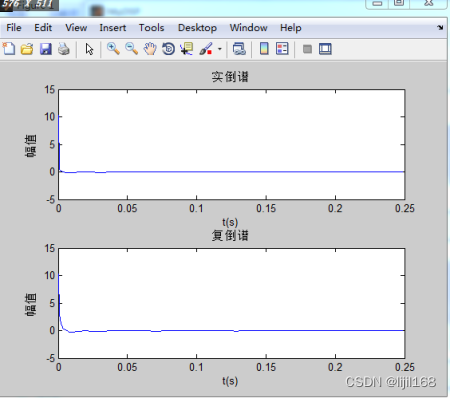
3、菜单“谱分析”->“STFT功率谱”，设置窗口点数、重叠点数和FFT点数，得到STFT功率谱图。

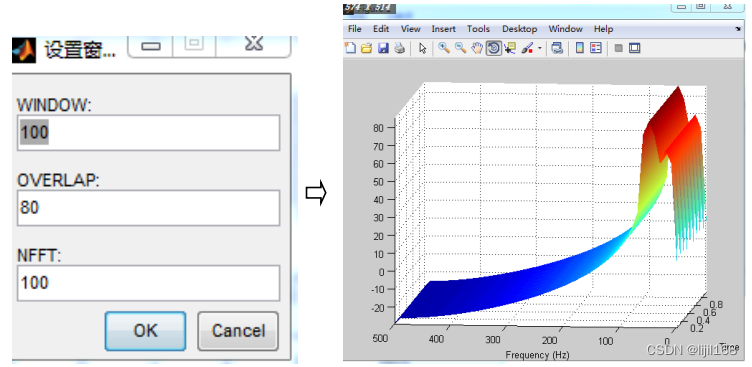
4、菜单“谱分析”->“小波时频谱”，设置尺度系数、小波函数和纵坐标，得到小波变换的时频谱图。

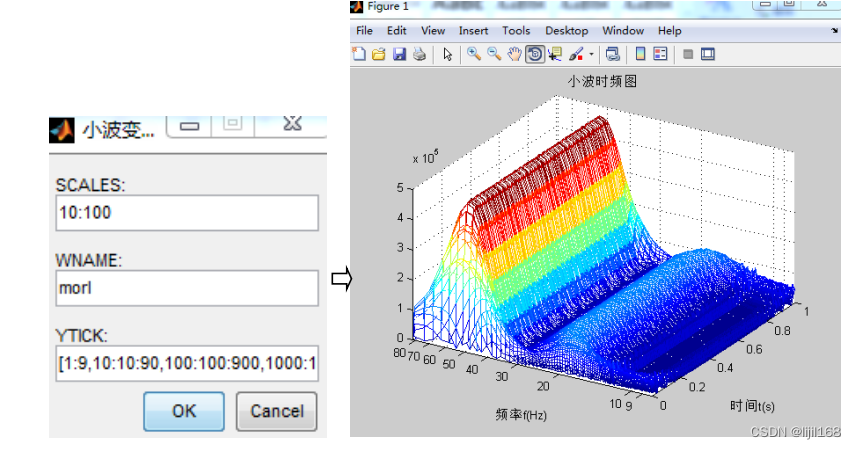
(七)小波分析。
小波分析包括小波分解和小波重构，和傅里叶变换类似，小波分解可以把原始信号分解为不能频率段的信号，小波重构可以把分解后的不能频段的信号重组成原信号，可用于信号降噪，也可用于将关心的信号提取出来。
商业软件不提供小波分解的功能。
1、小波分解。菜单“小波分析”->“小波多层分解”，设置小波分解层数、小波函数名得到小波分解的近似系数（低频系数），和细节系数（高频系数）。

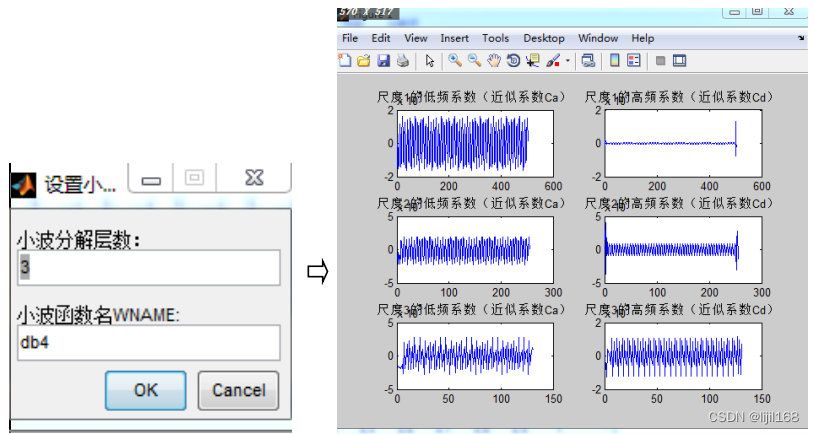
2、小波单支重构。菜单“小波分析”->“小波多层分解”，设置小波重构的层数、重构的类型、小波函数名得到重构的信号。

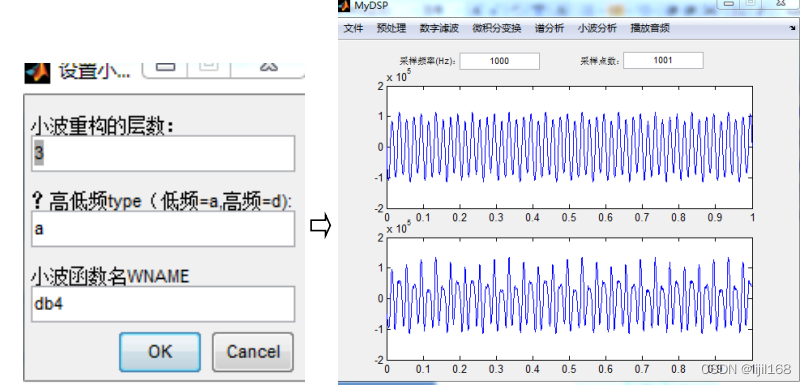
3、小波GUI工具箱。菜单“小波分析”->“小波GUI工具箱”，调出Matlab自带的小波工具箱，进行深入的小波分析研究。

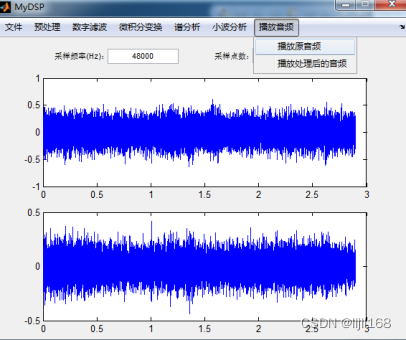
(八)播放音频。菜单“播放音频”->“播放原音频”，播放原始信号；菜单“播放音频”->“播放处理后的音频”，播放处理后的信号。

(九)希尔伯特变换
傅里叶变换和小波变换都只能得到一段时间范围内的频率信息，无法得到信号的瞬时频率，借助希尔伯特变换，可以把实信号变成复信号，进而得到信号的瞬时频率、瞬时相位和瞬时振幅，这对故障诊断有重要意义。因为当系统出现故障时，故障通常会对系统信号产生调制作用，使系统的响应信号振幅产生周期性的变化（调幅），或者频率产生周期性的变化（调频），这种周期性变化的频率对应于故障发生的频率，变化的大小对应于故障的强弱，经过本软件希尔伯特变换得到瞬时频率和瞬时振幅，即可找到故障发生的频率和故障强弱，希尔伯特变换在故障诊断中具有广泛的运用。
商业软件不提供希尔伯特变换功能。
1、导入自己设计的经过振幅调制和频率（相位）调制的信号：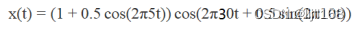

，

该信号受到5Hz的振幅调制和10Hz的频率调制（或相位调制），载波频率为30Hz，对应于正常系统的响应信号，5Hz的振幅调制信号和10Hz的频率调制（或相位调制）信号对应于故障信号，也就是故障发生的频率是5Hz和10Hz。

2、解调制->希尔伯特变换

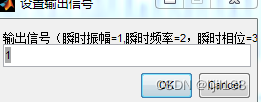
3、设置需要输出的信号

4、查看希尔伯特变换的结果：瞬时振幅、瞬时频率和瞬时相位，并输出选定的信号到程序界面，便于做进一步的处理。

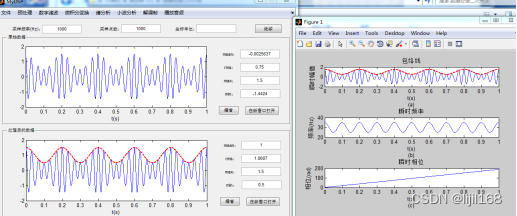
从瞬时振幅（包络图）可看出，载波信号经5HZ的振幅调制；从瞬时频率图可看出，载波经过10HZ的频率调制，调制的最大频率为5HZ，所以载波经调制后的瞬时频率波动范围为30HZ±5HZ，波动的频率为10HZ，载波频率为30HZ，在NVH故障分析中，10Hz就对应为故障发生的频率，找到对应的工作频率的零件，就可以找到故障源。
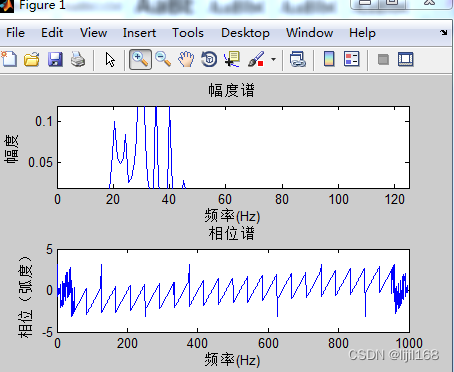
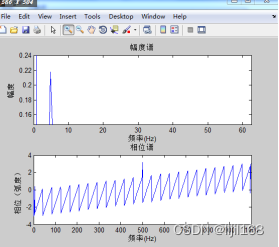
5、将调制后的信号进行FFT变换：频分析->频谱，可看出以30HZ的载波频率为中心，间隔5HZ及10HZ的边频（调制信号的频率），通过边频分析定位故障源也是NVH故障分析的一种方法。

6、点击“继续”命令，可对瞬时振幅（包络）信号进行进一步处理。

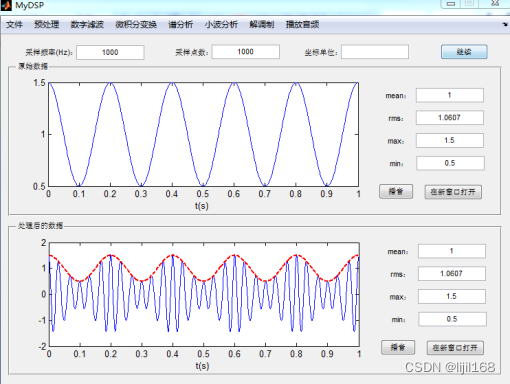
7、频分析->频谱，可看出包络信号的频率为5HZ，这就是振幅调制信号的频率。在NVH故障分析中，这就是故障发生的频率，找到对应的工作频率的零件，就可以找到故障源。

(十)EMD、VMD
希尔伯特变换虽然能得到信号的瞬时振幅、瞬时频率和瞬时相位，但是，希尔伯特变换对信号有严格的要求，对任意信号进行希尔伯特变换，可能出现无法解释、缺乏实际意义的频率分量。Norden E. Hung等人对瞬时频率进行研究后发现，只有满足特定条件的信号，其瞬时频率才具有物理意义，并将此类信号成为：IMF/基本模式分量。一般信号可经EMD、VMD等变换后得到满足希尔伯特变换的信号，使希尔伯特变换后的瞬时频率有意义。
经验模态分解( empirical mode decomposition，EMD)是由美国国家宇航局的华裔科学家Norden e. Huang博士于1998年提出的一种新的处理非平稳信号的方法——希尔伯特——黄变化的重要组成部分。它是依据数据自身的时间尺度特征来进行信号分解，无须预先设定任何基函数，这一点与建立在先验性的谐波基函数和小波基函数上的傅里叶分解与小波分解方法具有本质性的差别。正是由于这样的特点，EMD 方法在理论上可以应用于任何类型的信号的分解。
变分模态分解VMD是另一种分解方法，该方法在2014年提出，目前资料很少，主要基于英文论文。该方法能实现EMD类似的功能，主要的不同之处是EMD分解仅依赖原始数据，分解的层数不可设定，而VMD则可设定分解的层数。
1.导入自己设计的含噪声的信号

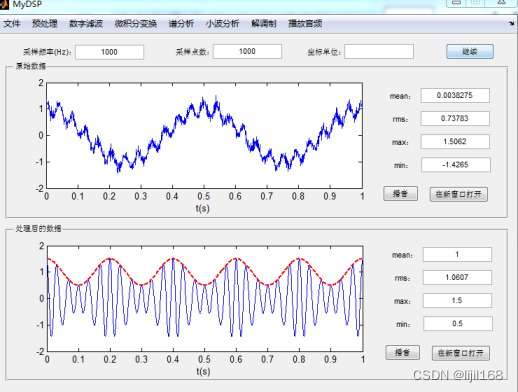
2、导入自己设计的含噪声的信号，EMD和VMD分解的结果如下图

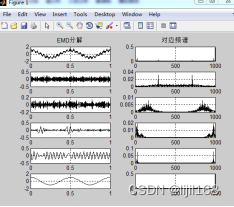
最后

以上就是暴躁钢铁侠为你收集整理的用matlab编写了一个DSP数据处理小软件的全部内容，希望文章能够帮你解决用matlab编写了一个DSP数据处理小软件所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。