因为逐渐有人将强化学习应用到 N L P NLP NLP 的任务上,有必要了解一些强化学习基础知识,本篇博文总结自台大教授李宏毅关于深度学习的公开课内容。
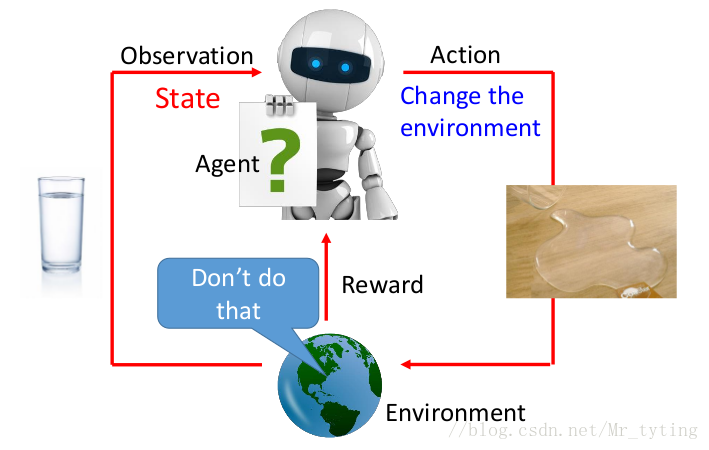
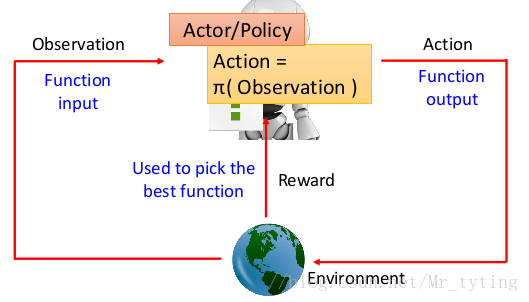
我们可以以上图来理解强化学习过程,我们机器人 a g e n t agent agent 通过 o b s e r v a t i o n observation observation 了解到环境的 S t a t e State State,采取一些 A c t i o n Action Action ,并且改变当前的环境,然后环境会反馈正向或负向的 r e w a r d reward reward 给 a g e n t agent agent。
举例来说,让机器人玩电玩游戏:
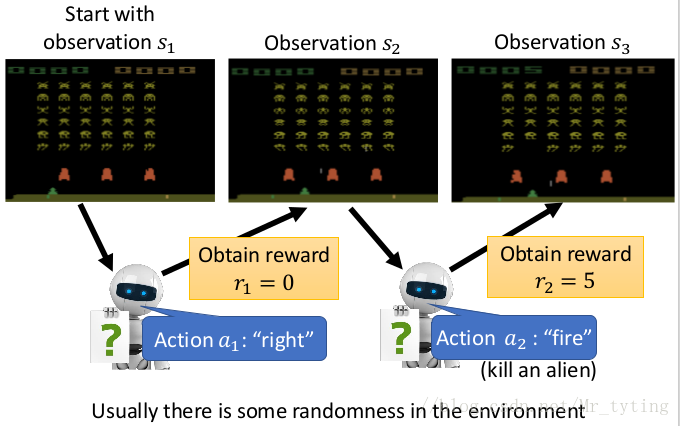
上图中 a g e n t agent agent 每次动作以后都可能随机的改变了环境,并且接受到一个 r e w a r d reward reward,由此观察改变后的环境,做出相应的动作。
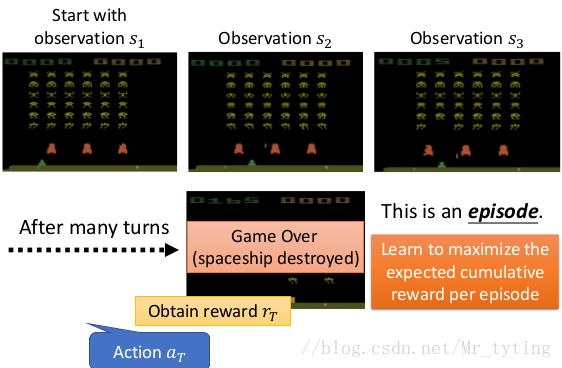
我们希望 a g e n t agent agent 多玩几个回合,并且***希望在每个回合中最大化的 t o t a l r e w a r d total reward total reward。***
强化学习难点:
-
R e w a r d d e l a y Reward delay Reward delay
例如上面所举得例子里,只有在开火时,才能获得 R e w a r d Reward Reward, a g e n t agent agent 学习的最后结果是会疯狂的开火,往左移或往右移,他觉得无所必要,但实际上移动对最后的 t o t a l R e w a r d total Reward total Reward 至关重要。还比如在下围棋时,短期的牺牲可能或换来最后的胜利。 -
a g e n t agent agent 的行为,也即是 a c t i o n action action 会影响后续他看到的环境。
Asynchronous Advantage Actor-Critic (A3C)
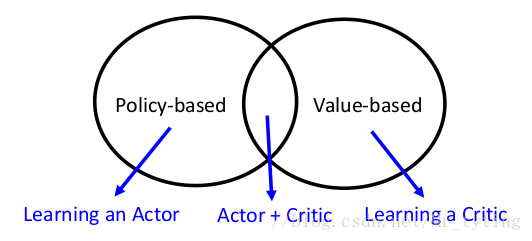
Policy-based Approach(Learning an Actor)
如果我们把 n e u r a l n e t w o r k neural network neural network 当做上面所讲的 a c t o r actor actor,那么:
- 模型的输入:即其观察到的环境(向量、矩阵等)
- 模型的输出:每一类动作在最后一层以一个神经元表示,对应其输出的***概率***。
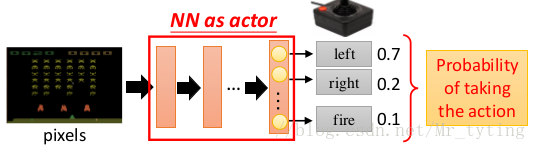
需要注意的是:在做 p o l i c y g r e d i e n t policy gredient policy gredient 时,是 s t o c h a s t i c stochastic stochastic 式的,也就是说其 o u t p u t output output 是一个机率,我们是一定的概率选取该动作,而不是一定选取。
那么如何决定这个 a c t i o n action action 的好坏呢?
我们假定 a c t o r actor actor 的模型为 π θ ( s ) pi_{theta}(s) πθ(s),这个 s s s 就是 a g e n t agent agent 所看到的环境, θ theta θ表示神经网络的参数。
我们拿这个 a c t o r actor actor 实际上去玩这个游戏:

如上图所示: a g e n t agent agent 玩完***一个回合*** 后,可以得到一个 t o t a l R e w a r d total Reward total Reward,而由上面的描述可知,这个 t o t a l r e w a r d total reward total reward 才是我们需要 m a x i m i z e maximize maximize 对象。
因为游戏的随机性,即使每个回合都采用一样的 a c t o r actor actor,在这里就是 a g e n t agent agent 模型一样,不同回合得到的 R θ R_theta Rθ 很有可能不一样,我们记: R ˉ θ bar{R}_{theta} Rˉθ 为该 a c t o r actor actor 的期望值,即使不同的回合,该 a c t o r actor actor 的期望值是相同的,这个期望值就衡量了 a c t o r actor actor 的好坏,好的期望值这个 a c t o r actor actor 就比较好。
那么这个期望值 R θ R_theta Rθ 如何得到呢?
假设一轮游戏所有经过表示为 τ tau τ ,则:
- τ = { s 1 , α 1 , r 1 , s 2 , α 2 , r 2 , s 3 , α 3 , r 3 , . . . , s T , α T , r T } tau={{s_1, alpha _1, r_1, s_2, alpha _2, r_2, s_3, alpha _3, r_3, ... , s_T, alpha _T, r_T}} τ={s1,α1,r1,s2,α2,r2,s3,α3,r3,...,sT,αT,rT}
- R ( τ ) = ∑ n = 1 T r n R(tau)=sum_{n=1}^{T}r_n R(τ)=∑n=1Trn
- 某一种 τ tau τ 出现的概率与 a c t o r actor actor (模型)有关,即该 τ tau τ 过程出现的概率为 P ( τ ∣ θ ) P(tau| theta) P(τ∣θ)
由上面的分析可知,某一个
a
c
t
o
r
actor
actor 一轮回合下来得到的
r
e
w
a
r
d
reward
reward 的期望值:
R
ˉ
θ
=
∑
τ
R
(
τ
)
p
(
τ
∣
θ
)
bar{R}_{theta}=sum_{tau}R(tau)p(tau|theta)
Rˉθ=τ∑R(τ)p(τ∣θ)
但是我们无法遍历所有的
τ
tau
τ,故只能采取抽样的方式,我们让这个
a
c
t
o
r
actor
actor 玩
N
N
N 场游戏,获得
N
N
N 个不同的游戏过程,即
{
τ
1
,
τ
2
,
.
.
.
.
,
τ
N
}
{tau^1, tau^2, ...., tau^N}
{τ1,τ2,....,τN},可以理解为从
p
(
τ
∣
θ
)
p(tau|theta)
p(τ∣θ) 中
s
a
m
p
l
e
sample
sample 了
N
N
N 次。即:
R
ˉ
θ
=
∑
τ
R
(
τ
)
p
(
τ
∣
θ
)
≈
1
N
∑
n
=
1
N
R
(
τ
n
)
bar{R}_{theta}=sum_{tau}R(tau)p(tau|theta)approx frac{1}{N}sum_{n=1}^{N}R(tau^n)
Rˉθ=τ∑R(τ)p(τ∣θ)≈N1n=1∑NR(τn)
那么现在已经找到了 R ˉ θ bar{R}_{theta} Rˉθ,我们希望找到了一个 θ ∗ theta^* θ∗,能 m a x θ R ˉ θ underset{theta}{max} bar{R}_{theta} θmaxRˉθ,也就是 θ ∗ = a r g m a x θ R ˉ θ theta^*=argunderset{theta}{max}bar{R}_{theta} θ∗=argθmaxRˉθ,我们可以利用 G r a d i e n t a s c e n t Gradient ascent Gradient ascent 来不断逼近:
- s t a r t w i t h θ 0 start with theta^0 start with θ0
- θ 1 ← θ 0 + η ▽ R ˉ θ 0 theta^1leftarrow theta^0+eta triangledown bar{R}_{theta^0} θ1←θ0+η▽Rˉθ0
- θ 2 ← θ 1 + η ▽ R ˉ θ 1 theta^2leftarrow theta^1+eta triangledown bar{R}_{theta^1} θ2←θ1+η▽Rˉθ1
- …
那么 ▽ R ˉ θ triangledown bar{R}_{theta} ▽Rˉθ 怎么求呢?
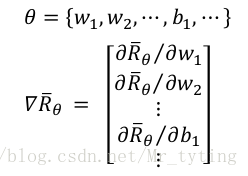
可以实际的推导一下 ▽ R ˉ θ triangledown bar{R}_{theta} ▽Rˉθ:

其中:
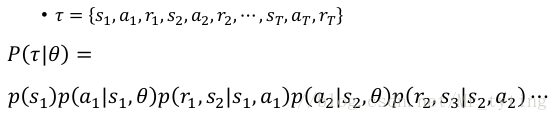
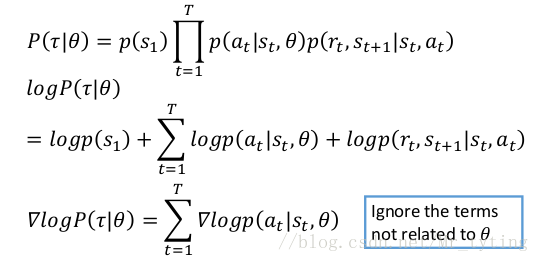
则:
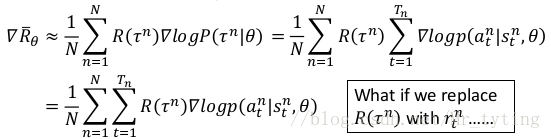
可以直观的理解上面 ▽ R ˉ θ triangledown bar{R}_{theta} ▽Rˉθ 结果:
- 当 R ( τ n ) R(tau^n) R(τn))(***注意这里是一个回合的 r e w a r d reward reward***) 为正的时候,我们希望调整 θ theta θ,增大 p ( α t n ∣ s t n ) p(alpha_t^n|s_t^n) p(αtn∣stn) ,使其在时间 t t t 更大可能选择 α t n alpha_t^n αtn
- 当 R ( τ n ) R(tau^n) R(τn) 为正的时候,我们希望调整 θ theta θ,减小 p ( α t n ∣ s t n ) p(alpha_t^n|s_t^n) p(αtn∣stn) ,使其在时间 t t t 更小可能选择 α t n alpha_t^n αtn
上面的求 ▽ R ˉ θ triangledown bar{R}_{theta} ▽Rˉθ 过程就是 p o l i c y G r a d i e n t policy Gradient policy Gradient。
Critic
给定一个 a c t o r π actor pi actor π,用 C r i t i c Critic Critic 来衡量 a c t o r actor actor 好或者不好,记做 V π ( s ) V^{pi}(s) Vπ(s),这里 s s s 就是当前的环境状态。 V π ( s ) V^{pi}(s) Vπ(s) 就是当观察到 s s s 后,到一轮游戏结束,我们所能得到的 r e w a r d reward reward 的期望值有多大。以此来更新 a c t o r actor actor(即其中的参数)
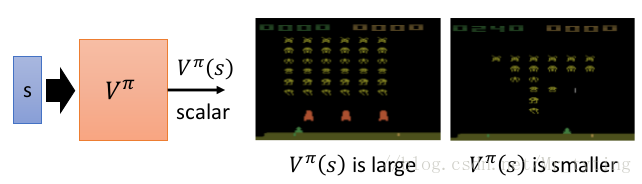
那么如何得到 V π ( s ) V^{pi}(s) Vπ(s) 呢?
Monte-Carlo
让 c r i t i c critic critic 观察 π pi π 玩游戏,举例来说:
- 当看到环境 s a s_a sa 后,直到一轮回合结束,所积累的 r e w a r d reward reward 为 G a G_a Ga,那么 V p i ( s a ) = G a V^{pi}(s_a) = G_a Vpi(sa)=Ga
- 当看到环境 s b s_b sb 后,直到一轮回合结束,所积累的 r e w a r d reward reward 为 G b G_b Gb,那么 V p i ( s b ) = G b V^{pi}(s_b) = G_b Vpi(sb)=Gb
Temporal-Difference
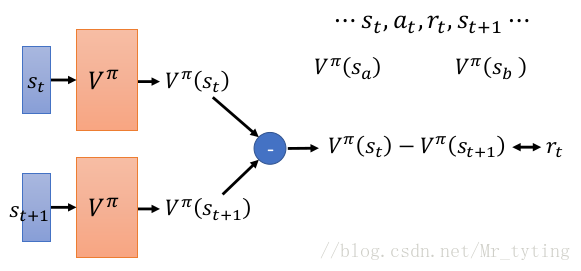
MC VS TD

不同的方法,其 V π ( s ) V^{pi}(s) Vπ(s) 值不一样,选哪个方法视具体情况而言。
Actor-Critic
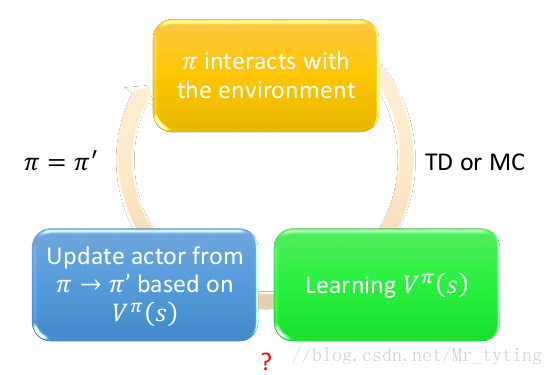
我们在上面讲到了 a c t o r actor actor 与环境互动时,会得到一个 r e w a r d reward reward 的反馈,如上面在求 ▽ R ˉ θ triangledown bar{R}_{theta} ▽Rˉθ 时:
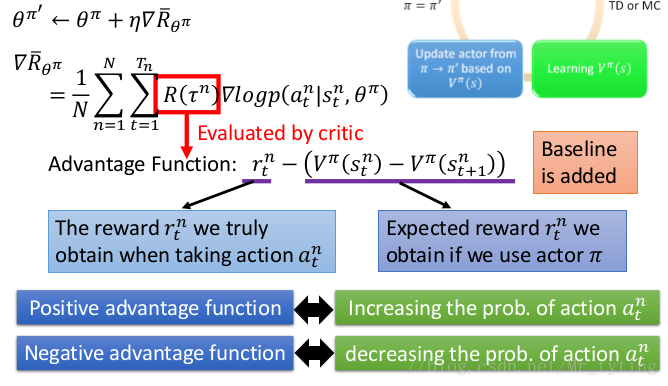
如上图所示,可以直接把 R ( / t a u n ) R(/tau^n) R(/taun) 看做 c r i t i c critic critic
Advantage Actor-Critic
对于 a c t o r π ( s ) actor pi(s) actor π(s) 和 c r i t i c V ( π s ) critic V^{pi}_(s) critic V(πs) 可以共享一些参数,如下图所示:
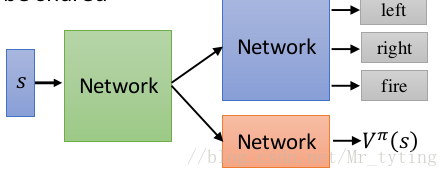
最后
以上就是忧虑期待最近收集整理的关于强化学习-->Deep Reinforcement Learning的全部内容,更多相关强化学习-->Deep内容请搜索靠谱客的其他文章。








发表评论 取消回复