Convergence rate
- 虽然optimization问题多用于基础研究,工程使用时有多种python库可供调用,但是了解其原理,一是有助于更好的选择optimization function,二是costumize自己的optimiation function(竞赛中常常用到)。
- 课程涉及大量推导,此处不分享相关slide.
- 首先看一下这篇https://zhuanlan.zhihu.com/p/27644403 ,对Convergence rate有一个大概的理解。
- 在发表optimization方向的论文时,需要尤其注意自己的模型属于哪种Convergence rate,并分析其表现: **_time and iteration count_**。
- 重点:Convergence rate only tells you how close each iteration gets to the best solution, however, it doesn't tell you how costly(timewise) each iteration is.**_ 解释一下就是,虽然有的optimization算法他Convergence rate很优秀,即可以几步就收敛到最优解,但是他每一次iteration的cost非常大,比如遍历整个数据集,或计算时间很长等,这就是trade-off,工程实现是需仔细考虑。
三种Convergence rate
-
Convergence rate:Sublinear < Linear < Quadratic (考)
- Sublinear:SGD (takes the amount of computations comparable with the total amount of the previous work.)
![]() (k是迭代次数,
(k是迭代次数,是k次迭代的risk值,Sublinear形式的特征是
在分母)
> Linear: GD (each new right digit of the answer takes a constant amount of computations)
![]() (Linear形式是k在指数)
(Linear形式是k在指数)
> Quadratic: 牛顿 (each iteration doubles the number of right digits in the answer,but expensive)
![]() (Quadratic形式)
(Quadratic形式)
(大家都用过的例子:SGD快,但是收敛效果不一定好,GD慢,但是遍历整个数据集,收敛效果好)
例如:你只是一个theoretician,不关心运行时间,你应该选择牛顿optimization,如果你是一个practitioner ,你应该选择DG或SGD。
optimization算法分析
(GD,SGD属于first order minimization,只保证收敛到stationary point, 而不保证收敛到local minima。)
GD----Linear convergence,以GD为例,讲解如何进行更好的optimization。
- 先我们希望需要去优化的loss function是strong convex并且smooth的(特别重要),基于这两个条件,可以证明GD算法属于linear convergence(证明见ppt19-21).(如果GD不可导,则需要使用subgradient代替gradient,此时推导过程基本不变)
- 如果只进行convex假设而不是strong convex,则GD的convergence rate只能退化成sublinear convergence rate,即正比于(1/t).
下面介绍如果并不满足strong convex假设,如何accelerate GD算法: Nesterov's Accelerated GD
- 思想: 每迈出一步,这一步的方向不光是当前的梯度方向,还要加一部分上一步得到的梯度。
- algorithm:(ppt-26)
Step1: 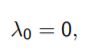
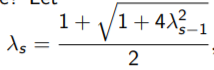
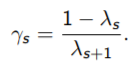
Step2: init:![]()
Step3: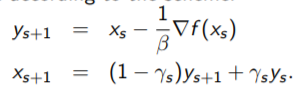
(第一行和GD完全一样,第二行加入了上一次的direction)
- torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)中使用这个参数,即在发现optimization funcction的convex性不是很好时将nesterov=False置为true,可得到1/t^2的convergence rate,虽然也是sublinear,但是比不加好很多。
- 源码阅读
- 如果从另一种证明方法得知,convergence rate反比与objective function的hessian矩阵的condition number,即smooth/convex。(strong vonvex:Q,convex: 根号Q),Q越小,收敛越快。)
(各大library不太会使用GD做优化器,但是GD方便手写,且是基础中的基础,和SGD是相同的,上面的方法在SGD中就用的很多了)
SGD----Sublinear
- 证明略。
- 如果objective function是strong convex的,convergence rate可证明:正比于log(t)。
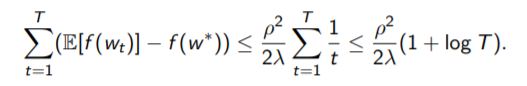
因为strong convex代表了slope更加steep,自然下降的更快。
(注意,GD的的步长一般认为是固定值(也有变化的),但是SGD的步长一般认为是变化的,到后面越来越慢![]() ,其中B是参数w的外界
,其中B是参数w的外界,
是当前vector的外界)。
- 步长: theoreticians 只证明SGD收敛可行,practitioners需要真正实现他,所以各个不同的Library都有自己的步长自适应算法,例如torch采用的Adagrad,RMSprop等,try to make two communities more agree with each other.
Newton method
虽然convergence rate很好,但是每次迭代expensive,因为要计算hessian矩阵的逆。
Quasi-Newton methods
因为first order的算法虽然convergence rate不太优秀,但是一次iteration计算资源消费较少,牛顿法则相反。所以提出了拟牛顿法这种改进。super-linear
首先,first order算法的迭代更新是
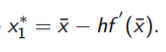
它满足approximation of the function f (x):(f(x)的一阶泰勒展开)
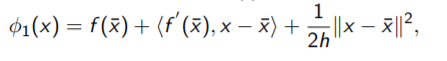
这个方程求极小值。(对他求一阶导,使一阶导为0)
同样,Newton methods迭代规则是:
![]()
它满足approximation of the function f (x):(二阶泰勒展开)
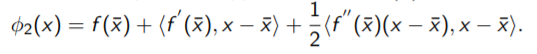
求极小值。
所以:Can we construct better approximations that φ1(x), but less expensive than φ2(x)?
它就是![]()
于是,f''(x)被替换成了G。
算法是:(H就是G-1)

如何更新H呢:
- BFGS
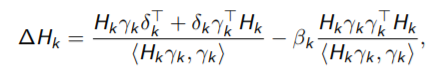
但是这样就会每次要存储一个n*n的矩阵,是昂贵的。
- LBFGS(减小存储空间)
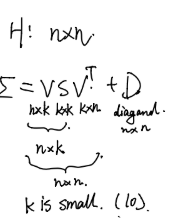
于是,只要存V这个矩阵就行了,前k个特征值被记录在S中。
-1的计算也给常快速:
![]()
最后放上使用SciPy库的代码(homework)
BFGS,LBFGS
The code was inspired by https://nbviewer.jupyter.org/github/fabianp/pytron/blob/master/doc/benchmark_logistic.ipynb
import numpy as np
import torch
import torch.nn as nn
import scipy.io as scio
from sklearn.gaussian_process import kernels
from tqdm import tqdm, trange
import scipy.stats as st
import torch
import numpy as np
from tqdm import tqdm, trange
import torch.nn.functional as F
import torch.nn as nn
from scipy.stats import logistic
import matplotlib.pyplot as plt
from torch.utils.data import TensorDataset, DataLoader, RandomSampler, SequentialSampler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
from scipy.optimize import minimize
from scipy import optimize
import numpy as np
from scipy import linalg, optimize
#
The code was inspired by https://nbviewer.jupyter.org/github/fabianp/pytron/blob/master/doc/benchmark_logistic.ipynb
def phi(t):
# logistic function
idx = t > 0
out = np.empty(t.size, dtype=np.float)
out[idx] = 1. / (1 + np.exp(-t[idx]))
exp_t = np.exp(t[~idx])
out[~idx] = exp_t / (1. + exp_t)
return out
def grad_hess(w, X, y, alpha):
# gradient AND hessian of the logistic
z = X.dot(w)
z = phi(y * z)
z0 = (z - 1) * y
grad = X.T.dot(z0) + alpha * w
def Hs(s):
d = z * (1 - z)
wa = d * X.dot(s)
return X.T.dot(wa) + alpha * s
return grad, Hs
def loss(w, X, y, alpha):
# loss function to be optimized, it's the logistic loss
z = X.dot(w)
yz = y * z
idx = yz > 0
out = np.zeros_like(yz)
out[idx] = np.log(1 + np.exp(-yz[idx]))
out[~idx] = (-yz[~idx] + np.log(1 + np.exp(yz[~idx])))
out = out.sum() + .5 * alpha * w.dot(w)
return out
def gradient(w, X, y, alpha):
# gradient of the logistic loss
z = X.dot(w)
z = phi(y * z)
z0 = (z - 1) * y
grad = X.T.dot(z0) + alpha * w
return grad
c = []
H= []
loss_ = []
res = []
for i in range(3):
data = scio.loadmat("data1.mat")
tr_x = np.asarray(data["TrainingX"])
tr_y = np.asarray(data["TrainingY"])
D = np.column_stack((tr_x, tr_y))
D1 = D[0:5000, :]
np.random.shuffle(D1)
D1 = D1[0:2000, :]
D2 = D[5000:, :]
np.random.shuffle(D2)
D2 = D2[0:2000, :]
train_xx = np.row_stack((D1[:, 0:784], D2[:, 0:784]))
train_y = np.row_stack((D1[:, 784:], D2[:, 784:]))
train_y = [arr[0] for arr in train_y]
print(np.shape(train_y))
train_x = metrics.pairwise.rbf_kernel(train_xx, train_xx)
m, n = np.shape(train_x)
te_x = np.asarray(data["TestX"])
test_y = np.asarray(data["TestY"])
test_x = metrics.pairwise.rbf_kernel(te_x, train_xx)
w = np.random.random((1, n))
alpha = 1.
X = train_x
y = train_y
print('BFGS')
timings_bfgs = []
precision_bfgs = []
w0 = np.zeros(X.shape[1])
def callback(x0):
prec = linalg.norm(gradient(x0, X, y, alpha), np.inf)
precision_bfgs.append(prec)
l = loss(x0,X, y, alpha)
loss_.append(l)
ht = np.dot(test_x, x0)
ht = phi(ht)
count = 0
for i in range(np.shape(ht)[0]):
if (ht[i] > 0.5):
s = 1
else:
s = -1
if (s != test_y[i]):
count = count + 1
c.append(count / 1000.)
print(count / 1000.)
_,K= grad_hess(x0,X, y, alpha)
H.append(K)
callback(w0)
out = optimize.fmin_bfgs(loss, w0, fprime=gradient,
args=(X, y, alpha), gtol=1e-10, maxiter=100,
callback=callback)
最后
以上就是舒适刺猬最近收集整理的关于机器学习中optimization问题 Convergence rate optimization算法分析的全部内容,更多相关机器学习中optimization问题内容请搜索靠谱客的其他文章。
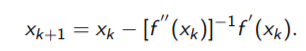








发表评论 取消回复