信号延迟实现方式信号

1、信号延迟的理论基础

在实际matlab仿真中，我们往往要实现信号的空间传播等等，这些实际上在不考虑信号的自由空间损耗的情况下，可以把空间传播看成一种信号的时延表示。
首先先带着大家复习一下信号与系统中傅里叶变换的时移特性。
傅里叶变换的时移特性是这样的：
假如

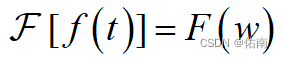
那么

从上面的公式中，我们可以看出，若对两个等式的两边同时取模的话，我们可以发现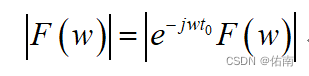

由此可以总结，信号发生时移，其频域的幅度谱不发生变化，变的是相位谱。
先看一下实验结果：

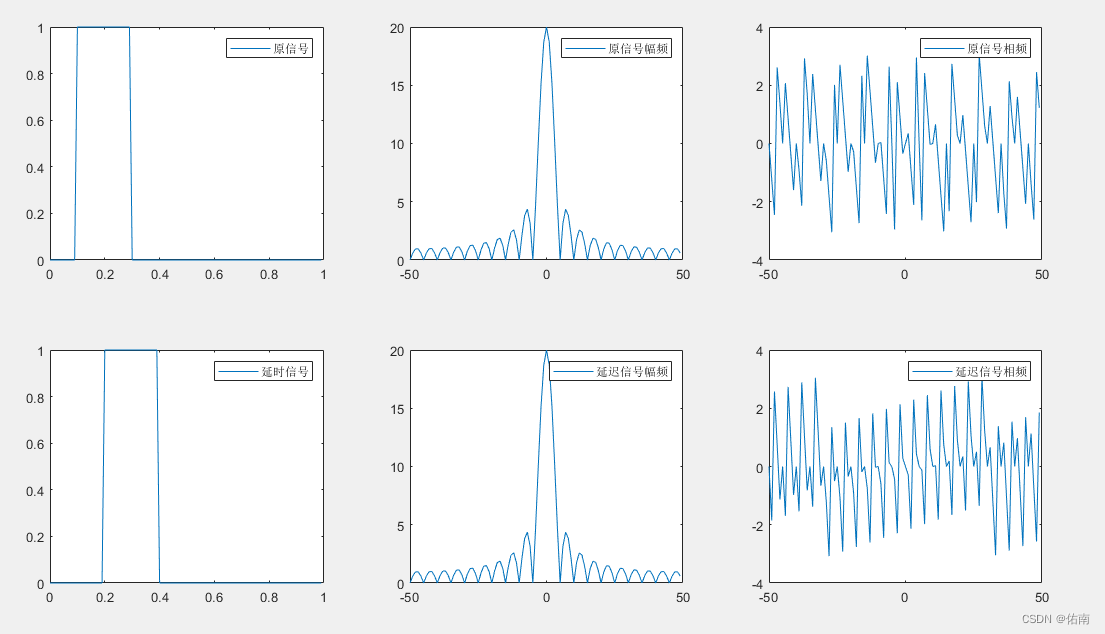
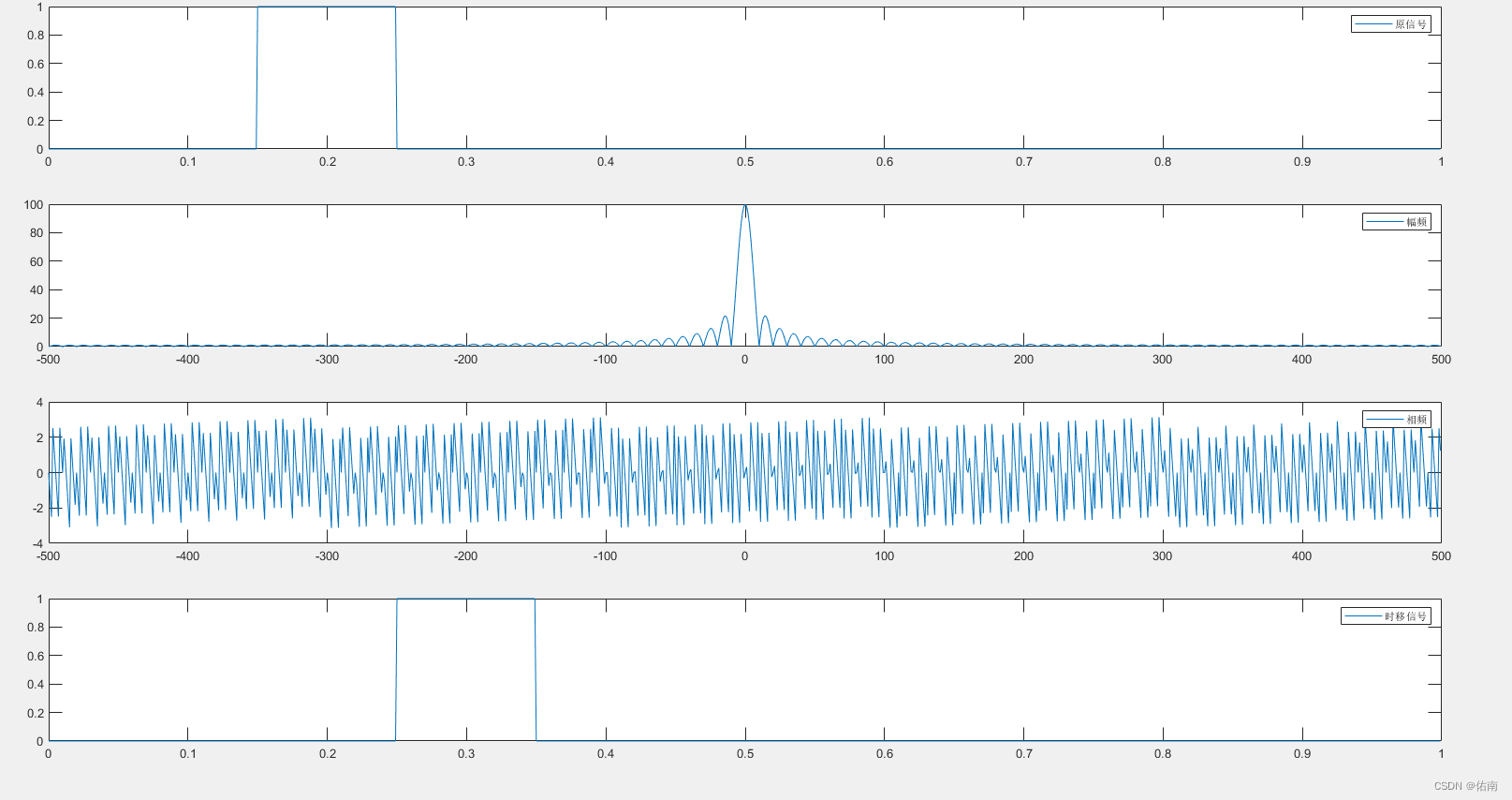
上面的实验结果，第一行代表的是原信号以及原信号的幅度谱和相位谱，原信号是一个矩形脉冲，中心为0.2，脉冲宽度为0.2。
第二行代表的是时移信号以及时移信号的幅度谱和相位谱，时移信号是将原信号进行延迟0.1所形成的的。通过对比两个信号的幅度谱和相位谱，可以得出信号发生时移，其频域的幅度谱不发生变化，变的是相位谱的结论。

2、信号时延的方法

2.1 时域处理方法

信号在matlab中就是一个数组的形式表示，我们在matlab中对信号进行时延操作其实就是对信号数组进行操作，明白了这点之后，就可以进行信号的时延操作了。（插零法）

实验如下
在实验中我们的信号时长为1秒，采样频率为1000，现在我们测试想要实现的是对一个宽度为0.1的距离门信号进行0.1s的时延。
其中重要步骤就是 时延点数=时延×采样频率，然后在原数组前面添加 采样点数个0，这是原信号数组长度变为 原长度＋时延点数，然后我们再取数组原信号长度个数。（阐述的有点啰嗦，我们结合例子来说吧）
例子中，信号时长1s，采样频率1000，则信号数组长度为1000（1×1000），时延0.1s，则需要在原信号数组前加上100（0.1×1000）个0，然后此时信号数组变为1100，与之前的信号数组长度不同，所以我们取前1000个赋值给一个变量，就相当于将原来的信号右移延迟。

fs = 1000;
gentime = 1;
t = (0:1:gentime*fs-1)/fs;
y1 = rectpuls(t-0.2,0.1);
figure;
subplot(211);plot(t,y1);legend('原信号');
delayNum = 0.1*fs;
y2 = [zeros(1,delayNum) y1];
y2 = y2(1:length(t));
subplot(212);plot(t,y2);legend('延迟信号');

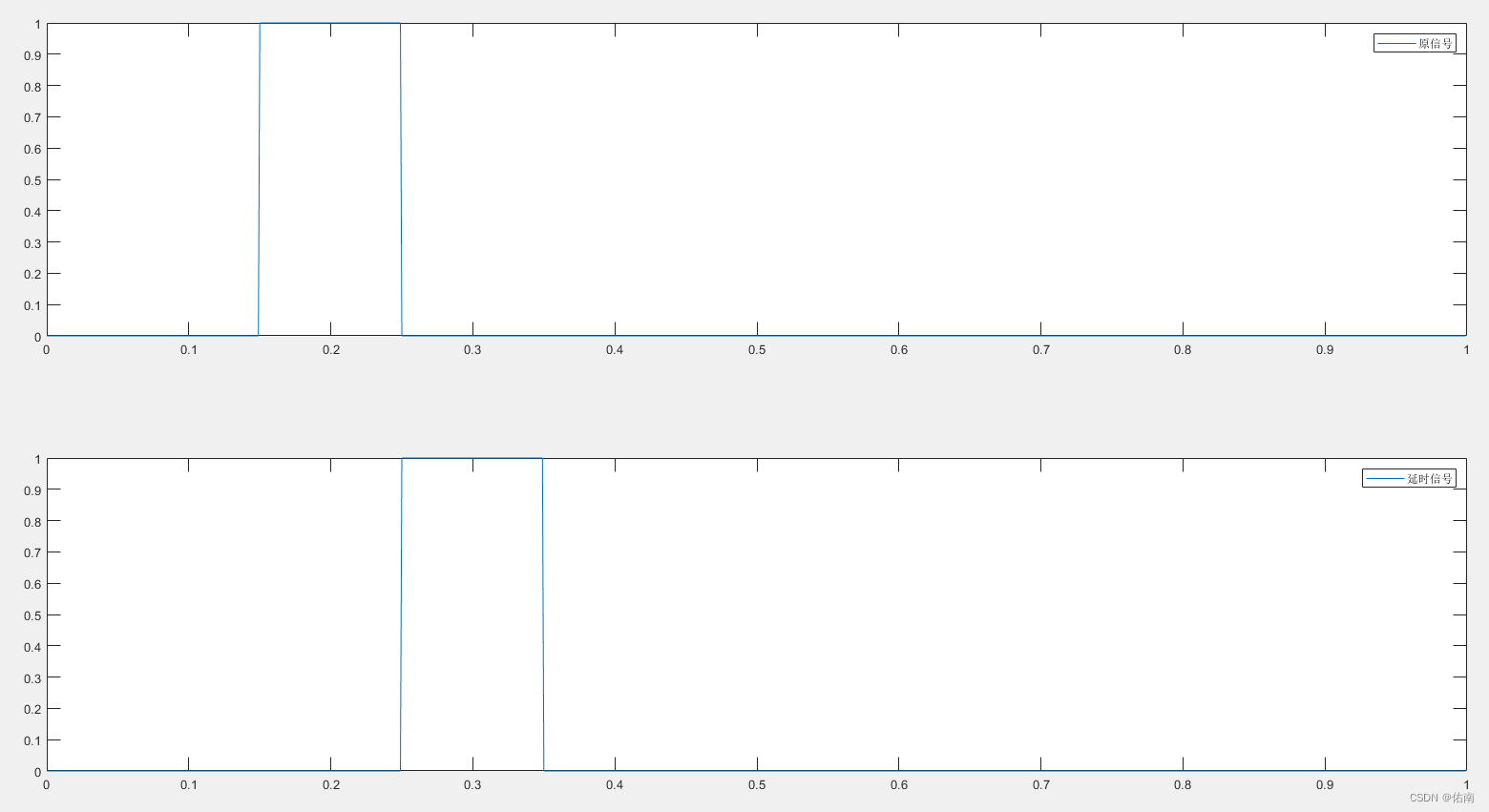
2.1 频域时延方法

频域的时延方法就没有什么好说的了，主要是利用傅里叶变换的时延特性来实现。
实现思路如下：先将原时域信号进行傅里叶变换——》获得频域信号，频域信号乘以e^(-jwτ)——》然后再进行反傅里叶变换——》得到延迟后的时域信号。

 fs = 1000;
gentime = 1;
t = (0:1:gentime*fs-1)/fs;
f = -fs/2:fs/2-1;
y1 = rectpuls(t-0.2,0.1);
subplot(411);plot(t,y1);legend('原信号');
Y1 =fft(y1);
% Y1 = fftshift(Y1);
subplot(412);plot(f,abs(fftshift(Y1)));legend('幅频');
subplot(413);plot(f,angle(Y1));legend('相频');
tao = 0.1;
Y2 = Y1.*exp(-1i*2*pi*f*tao);
s2 = ifft(Y2);
subplot(414);plot(t,real(s2));legend('延迟信号');

第一次写东西，如有错误尽请见谅…此致

最后

以上就是酷酷眼神为你收集整理的信号的时间延迟实现信号延迟实现方式信号的全部内容，希望文章能够帮你解决信号的时间延迟实现信号延迟实现方式信号所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。