分享自己的一篇文章，发布在中国智能系统会议（CISC2021），欢迎各位引用，引用格式为：
Zhao J, Dai F, Song Y. Consensus of Heterogeneous Mixed-Order Multi-agent Systems Including UGV and UAV. Proceedings of 2021 Chinese Intelligent Systems Conference. Springer, Singapore, 2022: 202-210.
无法下载的也可以联系我分享论文原文。原文中有一些打错字的情况，万分抱歉。
详细版代码地址为：Consensus_of_Heterogeneous_Mixed-order_Multi-agent_Systems_including_UGV_and_UAV
文章目录
- 摘要
- 1 介绍
- 2 预备知识
- 2.1 图论
- 引理 1 ([7])
- 例子 1
- 2.2 系统描述
- Remark 1
- Definition 1 （动态一致性）
- Definition 2 （静态一致性）
- 3 主要结果
- 3.1 一致性协议
- 3.2 稳定性分析
- 定理 1
- 证明
- 4 仿真
- 5 结论
- 程序代码
摘要
本文分析了在现有混合阶动态方程情况下，异构多智能体系统的一致性。混合阶智能体主要包括二阶智能体，以无人驾驶地面车辆（UGV）为例，以及高阶智能体，以无人驾驶航空器（UAV）为例。我们定义了系统的两类一致性，包括动态一致性和静态一致性。我们为这两种一致性的定义提出了相应的一致性控制协议。对于异构多智能体系统，我们通过结合两种提议的控制协议分析了系统的稳定性。并通过数值模拟的形式验证了控制协议的有效性。
1 介绍
作为一门新兴的复杂系统科学，多智能体系统在执行既定任务时具有单一智能体无法比拟的优势，如多无人驾驶地面车辆（UGV）系统的协同作战和多无人驾驶航空器（UAV）系统的编队性能。一致性问题是多智能体系统协调运行的基础。只有当智能体的个体状态一致时，他们才能进一步聚集和合作。
多智能体系统的研究通常分为三个部分，包括单个智能体的动力学模型，多个智能体之间的通信关系，以及多代理系统要实现一致时的控制协议。目前，对多智能体的研究多以同构智能体为基础，对异构智能体的研究就更少。同时，异构智能体的顺序也大多是一样的。对混合阶的异构多智能体的研究就更少了。
Olfati-Saber等人 [1] 分析了具有切换拓扑结构和时间延迟的多智能体系统的一致性。Song [2] 分析了多智能体系统中存在一阶和二阶智能体时，异构智能体系统在离散时间内的一致性问题。Dong等人 [3] 研究了时变条件下无人机的系统编队。Yang等人 [4] 研究了关于无人机、无人地面飞行器（USV）和无人水下飞行器（UUV）的分布式控制。Shi等人 [5] 分析了线性和非线性条件下异构二阶多智能体系统的一致性问题。Zhao等人 [6] 分析了异构多智能体系统的一致性。
本文的主要贡献包括：1）设计了一个具有不等数量的混合阶智能体的异构多智能体系统合作架构；2）提出了静态和动态的一致性协议；3）分析了所提一致性协议下系统的稳定性。
2 预备知识
2.1 图论
在本文中，我们使用图论的拓扑结构来表示系统的通信关系。
我们将与无向图
G
G
G 相关的图拉普拉斯矩阵定义为
L
=
D
−
A
(1)
L = D - A tag{1}
L=D−A(1)
其中 D D D 是度矩阵， A A A 是邻接矩阵。
考虑到实际环境，信息流是双向的。也就是说，当智能体 i i i 检测到智能体 j j j 时， j j j 同时也检测到了 i i i。所以我们假设图 G G G 是无向的。
根据定义，拉氏矩阵的每一行和都为0。因此，拉氏矩阵总是有一个关于右特征向量 w r = ( 1 / n ) 1 n = ( 1 / n ) ( 1 , 1 , ⋯ , 1 ) T w_r = (1/ sqrt{n}) mathbf{1}_n = (1 / sqrt{n}) (1, 1, cdots, 1)^text{T} wr=(1/n)1n=(1/n)(1,1,⋯,1)T 的 0 特征值。
针对异构系统，我们将拉氏矩阵分割为以下四块
L
=
[
L
G
G
L
G
A
L
A
G
L
A
A
]
L= left[begin{matrix} L_{GG} & L_{GA} \ L_{AG} & L_{AA} \ end{matrix}right]
L=[LGGLAGLGALAA]
其中 L G G , L A A L_{GG}, L_{AA} LGG,LAA 分别表示同构无人设备之间的通信。 L G A , L A G L_{GA}, L_{AG} LGA,LAG 表示在异构系统 UGVs 和 UAVs 之间的通信。
引理 1 ([7])
针对一个 N × N N times N N×N 的拉氏矩阵， L L L， e − L t , ∀ t ≥ 0 e^{-L t}, forall t ge 0 e−Lt,∀t≥0 是一个有正对角元素的随机矩阵。如果 L L L 有一个唯一的 0 特征值，秩为 Rank ( L ) = N − 1 text{Rank}(L) = N-1 Rank(L)=N−1，它的左特征向量有 v = [ v 1 v 2 ⋯ v n ] T ≥ 0 v = [begin{matrix}v_1 & v_2 & cdots & v_n end{matrix}]^text{T} ge 0 v=[v1v2⋯vn]T≥0 且 1 N T v = 1 , L T v = 0 mathbf{1}_{N}^text{T} v = mathbf{1}, L^text{T} v = 0 1NTv=1,LTv=0，其中 t → ∞ , e − L t → 1 N v T t rightarrow infty, e^{-Lt} rightarrow mathbf{1}_{N} v^text{T} t→∞,e−Lt→1NvT。
论 文 中 引 理 写 错 了 ， 应 该 是 左 特 征 向 量 ， 论 文 中 写 成 了 左 特 征 值 red{论文中引理写错了，应该是左特征向量，论文中写成了左特征值} 论文中引理写错了，应该是左特征向量，论文中写成了左特征值
例子 1
存在一个 3 个 UGV，2 个 UAV 的系统。通信关系如图 1 所示。那么它的拉氏矩阵可以写成如下四部分的形式
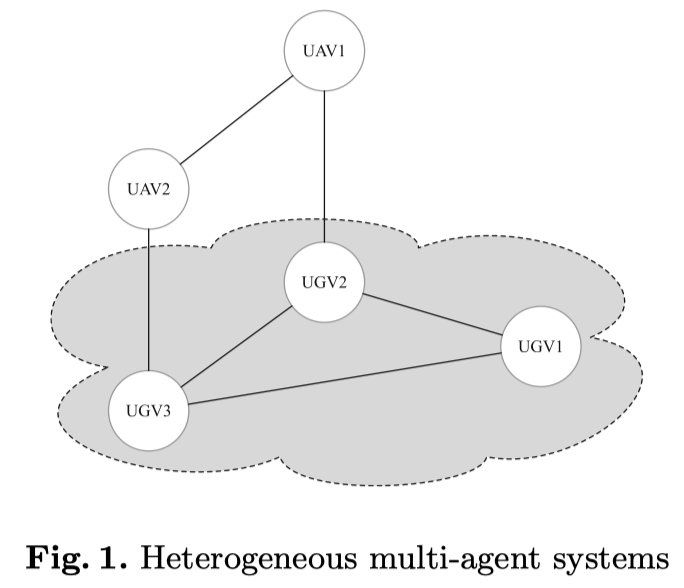
L
=
[
2
−
1
−
1
−
1
3
−
1
−
1
−
1
3
⏟
L
G
G
0
0
−
1
0
0
−
1
⏟
L
G
A
0
−
1
0
0
0
−
1
⏟
L
A
G
2
−
1
−
1
2
⏟
L
A
A
]
(3)
L= left[begin{matrix} underbrace{begin{matrix} 2 & -1 & -1 \ -1 & 3 & -1 \ -1 & -1 & 3 \ end{matrix}}_{L_{GG}} && underbrace{begin{matrix} 0 & 0 \ -1 & 0 \ 0 & -1 \ end{matrix}}_{L_{GA}} \\ underbrace{begin{matrix} 0 & -1 & 0 \ 0 & 0 & -1 \ end{matrix}}_{L_{AG}} && underbrace{begin{matrix} 2 & -1 \ -1 & 2 \ end{matrix}}_{L_{AA}} \ end{matrix}right] tag{3}
L=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡LGG
2−1−1−13−1−1−13LAG
00−100−1LGA
0−1000−1LAA
2−1−12⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤(3)
2.2 系统描述
二阶 UGV 动力学模型。
单个 UGV 的动力学模型为
p
˙
i
=
v
i
v
˙
i
=
u
i
(4)
begin{aligned} dot{p}_i =& v_i \ dot{v}_i =& u_i \ end{aligned} tag{4}
p˙i=v˙i=viui(4)
其中 p i = [ p i x , p i y ] T p_i = [p_i^x, p_i^y]^text{T} pi=[pix,piy]T 表示在 2-D 平面的运动， v i = [ v i x , v i y ] T v_i = [v_i^x, v_i^y]^text{T} vi=[vix,viy]T 表示 p i p_i pi 的速度， u i = [ u i x , u i y ] T u_i = [u_i^x, u_i^y]^text{T} ui=[uix,uiy]T 表示智能体 i i i 的输入。
针对
k
k
k 个 UGV 时，将（4）转换为状态空间形式
X
˙
G
=
A
G
⋅
X
G
+
B
G
⋅
U
G
(5)
begin{aligned} dot{X}_G = A_G cdot X_G + B_G cdot U_G end{aligned} tag{5}
X˙G=AG⋅XG+BG⋅UG(5)
其中
X
G
=
[
P
G
,
V
G
]
T
X_G = [P_G, V_G]^text{T}
XG=[PG,VG]T,
A
G
=
[
0
2
k
×
2
k
1
2
k
×
2
k
0
2
k
×
2
k
0
2
k
×
2
k
]
A_G = left[begin{matrix} 0_{2k times 2k} & 1_{2k times 2k} \ 0_{2k times 2k} & 0_{2k times 2k} \ end{matrix}right]
AG=[02k×2k02k×2k12k×2k02k×2k],
B
G
=
[
0
2
k
×
2
k
1
2
k
×
2
k
]
B_G = left[begin{matrix} 0_{2k times 2k} \ 1_{2k times 2k} \ end{matrix}right]
BG=[02k×2k12k×2k],
U
G
=
[
u
1
x
u
1
y
u
2
x
u
2
y
⋯
u
k
x
u
k
y
]
T
U_G = left[begin{matrix} u_1^x & u_1^y & u_2^x & u_2^y & cdots & u_k^x & u_k^y \ end{matrix}right]^text{T}
UG=[u1xu1yu2xu2y⋯ukxuky]T,
P
G
=
[
p
1
x
p
1
y
p
2
x
p
2
y
⋯
p
k
x
p
k
y
]
P_G = left[begin{matrix} p_1^x & p_1^y & p_2^x & p_2^y & cdots & p_k^x & p_k^y \ end{matrix}right]
PG=[p1xp1yp2xp2y⋯pkxpky],
V
G
=
[
v
1
x
v
1
y
v
2
x
v
2
y
⋯
v
k
x
v
k
y
]
V_G = left[begin{matrix} v_1^x & v_1^y & v_2^x & v_2^y & cdots & v_k^x & v_k^y \ end{matrix}right]
VG=[v1xv1yv2xv2y⋯vkxvky].
高阶 UAV 动力学模型。
参考 [4,7]，我们采用如下 UAV 的模型
x
¨
=
g
θ
y
¨
=
−
g
ϕ
z
¨
=
f
z
/
m
−
g
ϕ
¨
=
M
ϕ
/
I
x
θ
¨
=
M
θ
/
I
y
ψ
¨
=
M
ψ
/
I
z
(6)
begin{aligned} ddot{x} &= g theta \ ddot{y} &= -g phi \ ddot{z} &= f_z / m - g \ ddot{phi} &= M_phi / I_x \ ddot{theta} &= M_theta / I_y \ ddot{psi} &= M_psi / I_z \ end{aligned} tag{6}
x¨y¨z¨ϕ¨θ¨ψ¨=gθ=−gϕ=fz/m−g=Mϕ/Ix=Mθ/Iy=Mψ/Iz(6)
其中 g g g 是重力加速度。 x , y , z x,y,z x,y,z 是三轴位置。 ϕ , θ , ψ phi, theta, psi ϕ,θ,ψ 分别为无人机的滚转角、俯仰角、偏航角。 f z f_z fz 是在高度方向上的升力。 M ϕ , M θ , M ψ M_phi, M_theta, M_psi Mϕ,Mθ,Mψ 是机体坐标系中三轴方向上的力矩。 I x , I y , I z I_x, I_y, I_z Ix,Iy,Iz 分别是在机体坐标系中的惯性矩。
针对
l
l
l 个 UAVs，转化（6）为状态空间形式
X
˙
A
=
A
A
⋅
X
A
+
B
A
⋅
U
A
(7)
begin{aligned} dot{X}_A = A_A cdot X_A + B_A cdot U_A end{aligned} tag{7}
X˙A=AA⋅XA+BA⋅UA(7)
其中
X
A
=
[
P
A
,
V
A
,
Ω
A
,
Ω
˙
A
]
T
X_A = [P_A, V_A, Omega_A, dot{Omega}_A]^text{T}
XA=[PA,VA,ΩA,Ω˙A]T,
A
A
=
[
0
3
l
×
3
l
1
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
1
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
1
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
]
A_A = left[begin{matrix} 0_{3l times 3l} & 1_{3l times 3l} 0_{3l times 3l} & 0_{3l times 3l} \ 0_{3l times 3l} & 0_{3l times 3l} 1_{3l times 3l} & 0_{3l times 3l} \ 0_{3l times 3l} & 0_{3l times 3l} 0_{3l times 3l} & 1_{3l times 3l} \ 0_{3l times 3l} & 0_{3l times 3l} 0_{3l times 3l} & 0_{3l times 3l} \ end{matrix}right]
AA=⎣⎢⎢⎡03l×3l03l×3l03l×3l03l×3l13l×3l03l×3l03l×3l13l×3l03l×3l03l×3l03l×3l03l×3l03l×3l03l×3l13l×3l03l×3l⎦⎥⎥⎤,
B
A
=
[
0
3
l
×
3
l
0
3
l
×
3
l
0
3
l
×
3
l
1
3
l
×
3
l
]
B_A = left[begin{matrix} 0_{3l times 3l} \ 0_{3l times 3l} \ 0_{3l times 3l} \ 1_{3l times 3l} \ end{matrix}right]
BA=⎣⎢⎢⎡03l×3l03l×3l03l×3l13l×3l⎦⎥⎥⎤,
U
A
=
[
u
1
x
u
1
y
u
1
z
u
2
x
u
2
y
u
2
z
⋯
u
l
x
u
l
y
u
l
z
]
T
U_A = left[begin{matrix} u_1^x & u_1^y & u_1^z & u_2^x & u_2^y & u_2^z & cdots & u_l^x & u_l^y & u_l^z \ end{matrix}right]^text{T}
UA=[u1xu1yu1zu2xu2yu2z⋯ulxulyulz]T.
为了简化计算，我们假设 UAV 飞行在固定高度。也就是说，在 Z-轴方向上的控制输入为 0。于是
P
A
=
[
p
1
x
p
1
y
p
1
z
p
2
x
p
2
y
p
2
z
⋯
p
l
x
p
l
y
p
l
z
]
P_A = left[begin{matrix} p_1^x & p_1^y & p_1^z & p_2^x & p_2^y & p_2^z & cdots & p_l^x & p_l^y & p_l^z \ end{matrix}right]
PA=[p1xp1yp1zp2xp2yp2z⋯plxplyplz],
V
A
=
[
v
1
x
v
1
y
v
1
z
v
2
x
v
2
y
v
2
z
⋯
v
l
x
v
l
y
v
l
z
]
V_A = left[begin{matrix} v_1^x & v_1^y & v_1^z & v_2^x & v_2^y & v_2^z & cdots & v_l^x & v_l^y & v_l^z \ end{matrix}right]
VA=[v1xv1yv1zv2xv2yv2z⋯vlxvlyvlz],
Ω
A
=
[
g
θ
1
−
g
ϕ
1
0
g
θ
2
−
g
ϕ
2
0
⋯
g
θ
l
−
g
ϕ
l
0
]
Omega_A = left[begin{matrix} g theta_1 & -g phi_1 & 0 & g theta_2 & -g phi_2 & 0 & cdots & g theta_l & -g phi_l & 0 \ end{matrix}right]
ΩA=[gθ1−gϕ10gθ2−gϕ20⋯gθl−gϕl0],
Ω
˙
A
=
[
g
θ
˙
1
−
g
ϕ
1
˙
0
g
θ
˙
2
−
g
ϕ
˙
2
0
⋯
g
θ
˙
l
−
g
ϕ
˙
l
0
]
dot{Omega}_A = left[begin{matrix} g dot{theta}_1 & -g dot{phi_1} & 0 & g dot{theta}_2 & -g dot{phi}_2 & 0 & cdots & g dot{theta}_l & -g dot{phi}_l & 0 \ end{matrix}right]
Ω˙A=[gθ˙1−gϕ1˙0gθ˙2−gϕ˙20⋯gθ˙l−gϕ˙l0].
异构多智能体系统。
为了更方便地分析异构多智能体系统，我们将UGV模型（5）和UAV模型（7）整合为一个状态空间模型，以便清晰描述。结合前面提到的，异构多智能体系统的状态空间公式可以表示为
X
˙
=
A
⋅
X
+
B
⋅
U
(8)
begin{aligned} dot{X} = A cdot X + B cdot U end{aligned} tag{8}
X˙=A⋅X+B⋅U(8)
其中
X
=
[
X
G
T
,
X
A
T
]
T
X = [X_G^text{T}, X_A^text{T}]^text{T}
X=[XGT,XAT]T,
A
=
[
A
G
0
0
A
A
]
A = left[begin{matrix} A_G & 0 \ 0 & A_A \ end{matrix}right]
A=[AG00AA],
B
=
[
B
G
0
0
B
A
]
B = left[begin{matrix} B_G & 0 \ 0 & B_A \ end{matrix}right]
B=[BG00BA],
U
=
[
U
G
T
U
A
T
]
U = left[begin{matrix} U_G^text{T} & U_A^text{T} \ end{matrix}right]
U=[UGTUAT].
Remark 1
在本节中，我们首先描述了UGV和UAV的单智能体模型。其次，用状态空间方程来描述多个的UGV和UAV。最后，我们提出UGV和UAV的合作结构。
关于多智能体系统的一致性，我们提出以下两种类型：
Definition 1 （动态一致性）
当所有智能体的状态都满足以下条件时，系统就会达成动态一致性：
lim
t
→
∞
∥
p
i
(
t
)
−
p
j
(
t
)
∥
=
0
,
lim
t
→
∞
∥
v
i
(
t
)
−
v
j
(
t
)
∥
=
0
,
lim
t
→
∞
∥
ω
i
(
t
)
∥
=
0
,
lim
t
→
∞
∥
ω
˙
i
(
t
)
∥
=
0
,
i
,
j
=
1
,
2
,
⋯
,
n
(9)
begin{aligned} &lim_{t rightarrow infty} | p_i(t) - p_j(t) | = 0, \ &lim_{t rightarrow infty} | v_i(t) - v_j(t) | = 0, \ &lim_{t rightarrow infty} | omega_i(t) | = 0, \ &lim_{t rightarrow infty} | dot{omega}_i(t) | = 0, ~~~ i,j = 1,2,cdots,n \ end{aligned} tag{9}
t→∞lim∥pi(t)−pj(t)∥=0,t→∞lim∥vi(t)−vj(t)∥=0,t→∞lim∥ωi(t)∥=0,t→∞lim∥ω˙i(t)∥=0, i,j=1,2,⋯,n(9)
Definition 2 （静态一致性）
当所有智能体的状态都满足以下条件时，系统就会达成静态一致性：
lim
t
→
∞
∥
p
i
(
t
)
−
p
j
(
t
)
∥
=
0
,
lim
t
→
∞
∥
v
i
(
t
)
∥
=
0
,
lim
t
→
∞
∥
ω
i
(
t
)
∥
=
0
,
lim
t
→
∞
∥
ω
˙
i
(
t
)
∥
=
0
,
i
,
j
=
1
,
2
,
⋯
,
n
(10)
begin{aligned} &lim_{t rightarrow infty} | p_i(t) - p_j(t) | = 0, \ &lim_{t rightarrow infty} | v_i(t) | = 0, \ &lim_{t rightarrow infty} | omega_i(t) | = 0, \ &lim_{t rightarrow infty} | dot{omega}_i(t) | = 0, ~~~ i,j = 1,2,cdots,n \ end{aligned} tag{10}
t→∞lim∥pi(t)−pj(t)∥=0,t→∞lim∥vi(t)∥=0,t→∞lim∥ωi(t)∥=0,t→∞lim∥ω˙i(t)∥=0, i,j=1,2,⋯,n(10)
3 主要结果
3.1 一致性协议
针对上述的定义 1 和定义 2，我们提出下述两种类型一致性协议。
针对定义 1 的动态一致性协议分别为
（
UGV
）
u
i
=
α
∑
j
∈
N
i
a
i
j
(
P
j
−
P
i
)
+
β
∑
j
∈
N
i
a
i
j
(
V
j
−
V
i
)
,
i
=
1
,
2
,
⋯
,
k
.
（
UAV
）
u
i
=
α
∑
j
∈
N
i
a
i
j
(
P
j
−
P
i
)
+
β
∑
j
∈
N
i
a
i
j
(
V
j
−
V
i
)
−
γ
1
Ω
i
−
γ
2
Ω
˙
i
,
i
=
1
,
2
,
⋯
,
l
.
(11)
begin{aligned} （text{UGV}）u_i =& alpha sum_{j in N_i} a_{ij}(P_j - P_i) + beta sum_{j in N_i} a_{ij} (V_j - V_i), ~~~ i=1,2, cdots, k. \ （text{UAV}）u_i =& alpha sum_{j in N_i} a_{ij}(P_j - P_i) + beta sum_{j in N_i} a_{ij} (V_j - V_i) - gamma_1 Omega_i - gamma_2 dot{Omega}_i, ~~~ i=1,2, cdots, l. \ end{aligned} tag{11}
（UGV）ui=（UAV）ui=αj∈Ni∑aij(Pj−Pi)+βj∈Ni∑aij(Vj−Vi), i=1,2,⋯,k.αj∈Ni∑aij(Pj−Pi)+βj∈Ni∑aij(Vj−Vi)−γ1Ωi−γ2Ω˙i, i=1,2,⋯,l.(11)
其中 α > 0 , β > 0 , γ 1 > 0 , γ 2 > 0 alpha > 0, beta > 0, gamma_1 > 0, gamma_2 > 0 α>0,β>0,γ1>0,γ2>0 是控制因子。
结合拉氏矩阵（2），一致性协议可以表示为
U
=
−
L
d
⋅
X
(12)
U = - L_d cdot X tag{12}
U=−Ld⋅X(12)
其中
L
d
=
[
α
L
G
G
⊗
I
2
β
L
G
G
⊗
I
2
α
L
G
A
⊗
T
1
β
L
G
A
⊗
T
1
0
0
α
L
A
G
⊗
T
2
β
L
A
G
⊗
T
2
α
L
A
A
⊗
I
3
β
L
A
A
⊗
I
3
γ
1
I
l
⊗
I
3
γ
2
I
l
⊗
I
3
]
(13)
L_d = left[begin{matrix} alpha L_{GG} otimes I_2 & beta L_{GG} otimes I_2 & alpha L_{GA} otimes T_1 & beta L_{GA} otimes T_1 & 0 & 0 \ alpha L_{AG} otimes T_2 & beta L_{AG} otimes T_2 & alpha L_{AA} otimes I_3 & beta L_{AA} otimes I_3 & gamma_1 I_l otimes I_3 & gamma_2 I_l otimes I_3 \ end{matrix}right] tag{13}
Ld=[αLGG⊗I2αLAG⊗T2βLGG⊗I2βLAG⊗T2αLGA⊗T1αLAA⊗I3βLGA⊗T1βLAA⊗I30γ1Il⊗I30γ2Il⊗I3](13)
I I I 是单位矩阵， ⊗ otimes ⊗ 表示克罗尼克积， T 1 = [ 1 0 0 0 1 0 ] , T 2 = [ 1 0 0 1 0 0 ] T_1 = left[begin{matrix} 1 & 0 & 0 \ 0 & 1 & 0end{matrix}right], T_2 = left[begin{matrix} 1 & 0 \ 0 & 1 \ 0 & 0 \ end{matrix}right] T1=[100100],T2=⎣⎡100010⎦⎤。
针对定义 2 的静态一致性协议分别为
（
UGV
）
u
i
=
α
∑
j
∈
N
i
a
i
j
(
P
j
−
P
i
)
−
β
V
i
,
i
=
1
,
2
,
⋯
,
k
.
（
UAV
）
u
i
=
α
∑
j
∈
N
i
a
i
j
(
P
j
−
P
i
)
−
β
V
i
−
γ
1
Ω
i
−
γ
2
Ω
˙
i
,
i
=
1
,
2
,
⋯
,
l
.
(14)
begin{aligned} （text{UGV}）u_i =& alpha sum_{j in N_i} a_{ij}(P_j - P_i) - beta V_i, ~~~ i=1,2, cdots, k. \ （text{UAV}）u_i =& alpha sum_{j in N_i} a_{ij}(P_j - P_i) - beta V_i - gamma_1 Omega_i - gamma_2 dot{Omega}_i, ~~~ i=1,2, cdots, l. \ end{aligned} tag{14}
（UGV）ui=（UAV）ui=αj∈Ni∑aij(Pj−Pi)−βVi, i=1,2,⋯,k.αj∈Ni∑aij(Pj−Pi)−βVi−γ1Ωi−γ2Ω˙i, i=1,2,⋯,l.(14)
矩阵形式为
U
=
−
L
s
⋅
X
(15)
U = - L_s cdot X tag{15}
U=−Ls⋅X(15)
其中
L
s
=
[
α
L
G
G
⊗
I
2
β
L
k
⊗
I
2
α
L
G
A
⊗
T
1
0
0
0
α
L
A
G
⊗
T
2
0
α
L
A
A
⊗
I
3
β
L
l
⊗
I
3
γ
1
I
l
⊗
I
3
γ
2
I
l
⊗
I
3
]
(16)
L_s = left[begin{matrix} alpha L_{GG} otimes I_2 & beta L_{k} otimes I_2 & alpha L_{GA} otimes T_1 & 0 & 0 & 0 \ alpha L_{AG} otimes T_2 & 0 & alpha L_{AA} otimes I_3 & beta L_{l} otimes I_3 & gamma_1 I_l otimes I_3 & gamma_2 I_l otimes I_3 \ end{matrix}right] tag{16}
Ls=[αLGG⊗I2αLAG⊗T2βLk⊗I20αLGA⊗T1αLAA⊗I30βLl⊗I30γ1Il⊗I30γ2Il⊗I3](16)
3.2 稳定性分析
定理 1
假设 G = ( V , E , A ) G = (V,E,A) G=(V,E,A) 是连通无向图。异构混合阶系统（8）使用协议（11）且满足如下条件时，系统能达到动态一致。
α > 0 , β > 0 , γ 1 > 0 , γ 2 > 0 , β > > α , and γ 1 , γ 2 > β > > α , β γ 1 γ 2 > β 2 + γ 2 2 α begin{aligned} & alpha > 0, ~~~beta>0, ~~~gamma_1 > 0, ~~~gamma_2 > 0, \ & beta >> alpha, ~text{and}~ gamma_1, gamma_2 > beta >> alpha, \ & beta gamma_1 gamma_2 > beta^2 + gamma_2^2 alpha end{aligned} α>0, β>0, γ1>0, γ2>0,β>>α, and γ1,γ2>β>>α,βγ1γ2>β2+γ22α
证明
将（12）代入（8）
X
˙
=
Γ
d
⋅
X
(17)
dot{X} = Gamma_d cdot X tag{17}
X˙=Γd⋅X(17)
其中
Γ
d
=
[
0
1
0
0
0
0
α
L
G
G
⊗
I
2
β
L
G
G
⊗
I
2
α
L
G
A
⊗
T
1
β
L
G
A
⊗
T
1
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
α
L
A
G
⊗
T
2
β
L
A
G
⊗
T
2
α
L
A
A
⊗
I
3
β
L
A
A
⊗
I
3
γ
1
I
l
⊗
I
3
γ
2
I
l
⊗
I
3
]
Gamma_d = left[begin{matrix} 0 & 1 & 0 & 0 & 0 & 0 \ alpha L_{GG} otimes I_2 & beta L_{GG} otimes I_2 & alpha L_{GA} otimes T_1 & beta L_{GA} otimes T_1 & 0 & 0 \ 0 & 0 & 0 & 1 & 0 & 0 \ 0 & 0 & 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 0 & 0 & 1 \ alpha L_{AG} otimes T_2 & beta L_{AG} otimes T_2 & alpha L_{AA} otimes I_3 & beta L_{AA} otimes I_3 & gamma_1 I_l otimes I_3 & gamma_2 I_l otimes I_3 \ end{matrix}right]
Γd=⎣⎢⎢⎢⎢⎢⎢⎡0αLGG⊗I2000αLAG⊗T21βLGG⊗I2000βLAG⊗T20αLGA⊗T1000αLAA⊗I30βLGA⊗T1100βLAA⊗I300010γ1Il⊗I300001γ2Il⊗I3⎦⎥⎥⎥⎥⎥⎥⎤
根据线性系统稳定性定理。我们需要选择参数 α , β , γ 1 , γ 2 alpha, beta, gamma_1, gamma_2 α,β,γ1,γ2 使 Γ d Gamma_d Γd 有一个零特征值，其他特征值均有负实部。参数 α , β alpha, beta α,β 需要满足 UGV 一致性的稳定。参数 γ 1 , γ 2 gamma_1, gamma_2 γ1,γ2 需要满足 UAV 一致性的稳定性。更多细节可参考文献 [4]。
选定参数之后，
Γ
d
Gamma_d
Γd 可以转换为一个约当标准型 [1]：
Γ
d
=
P
J
P
−
1
Gamma_d = P J P^{-1}
Γd=PJP−1
令 v 1 T v_1^text{T} v1T 是 P − 1 P^{-1} P−1 的第一行，
4 仿真
我们对上述两种协议进行了数值模拟。假设一个由 3 个 UGV 和 2 个 UAV 组成的异构多智能体系统，其通信关系如图 1 所示。初始状态请参考原论文。
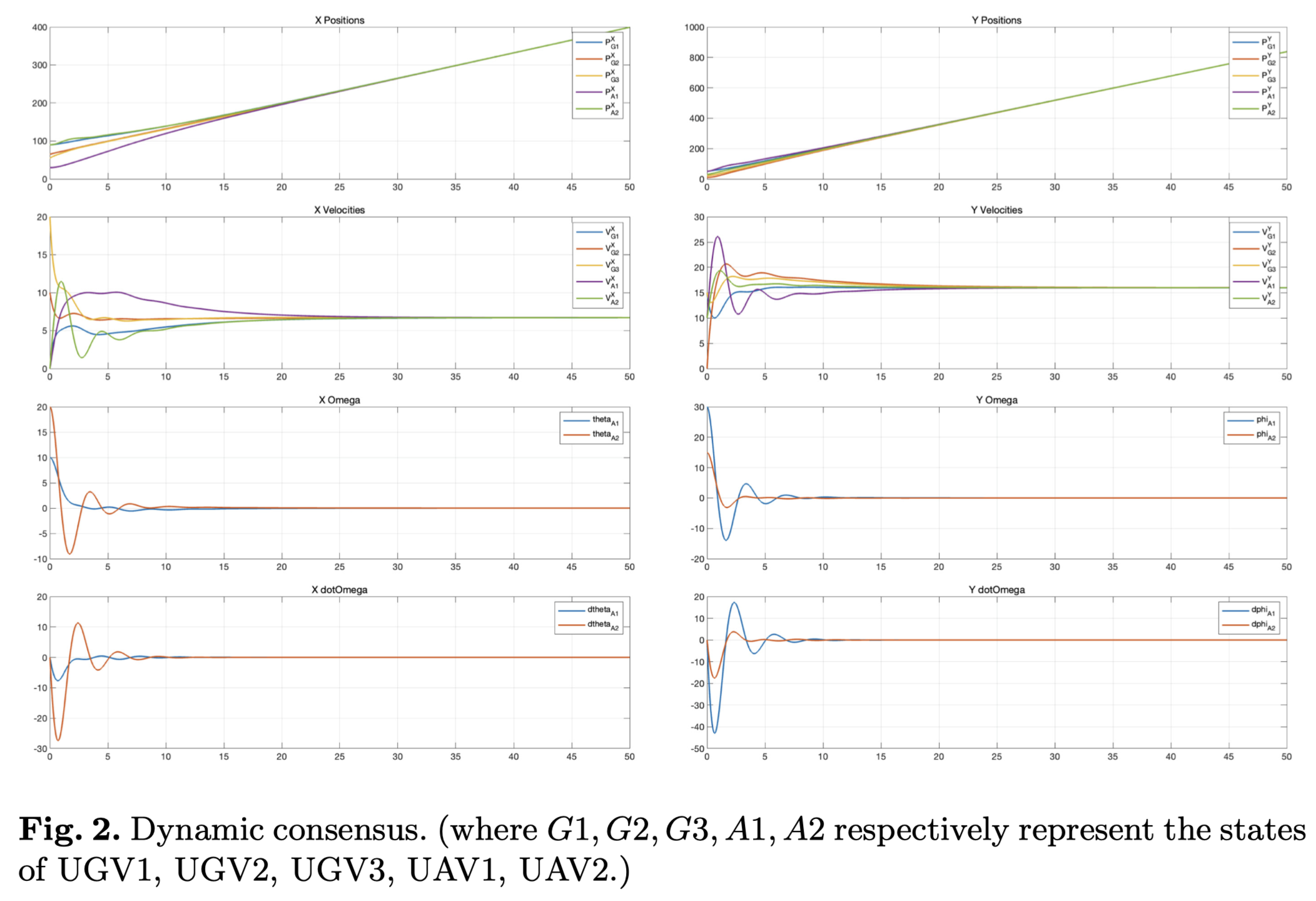
图 2 显示了系统在控制法则（11）下达到动态一致性。我们可以看到，当时间趋于无穷时，系统的速度是一致的。由于速度是一致而不是0，所以位置处于不断增加的状态。在系统达到动态一致后，位置增加的速度与一致后的速度相等。
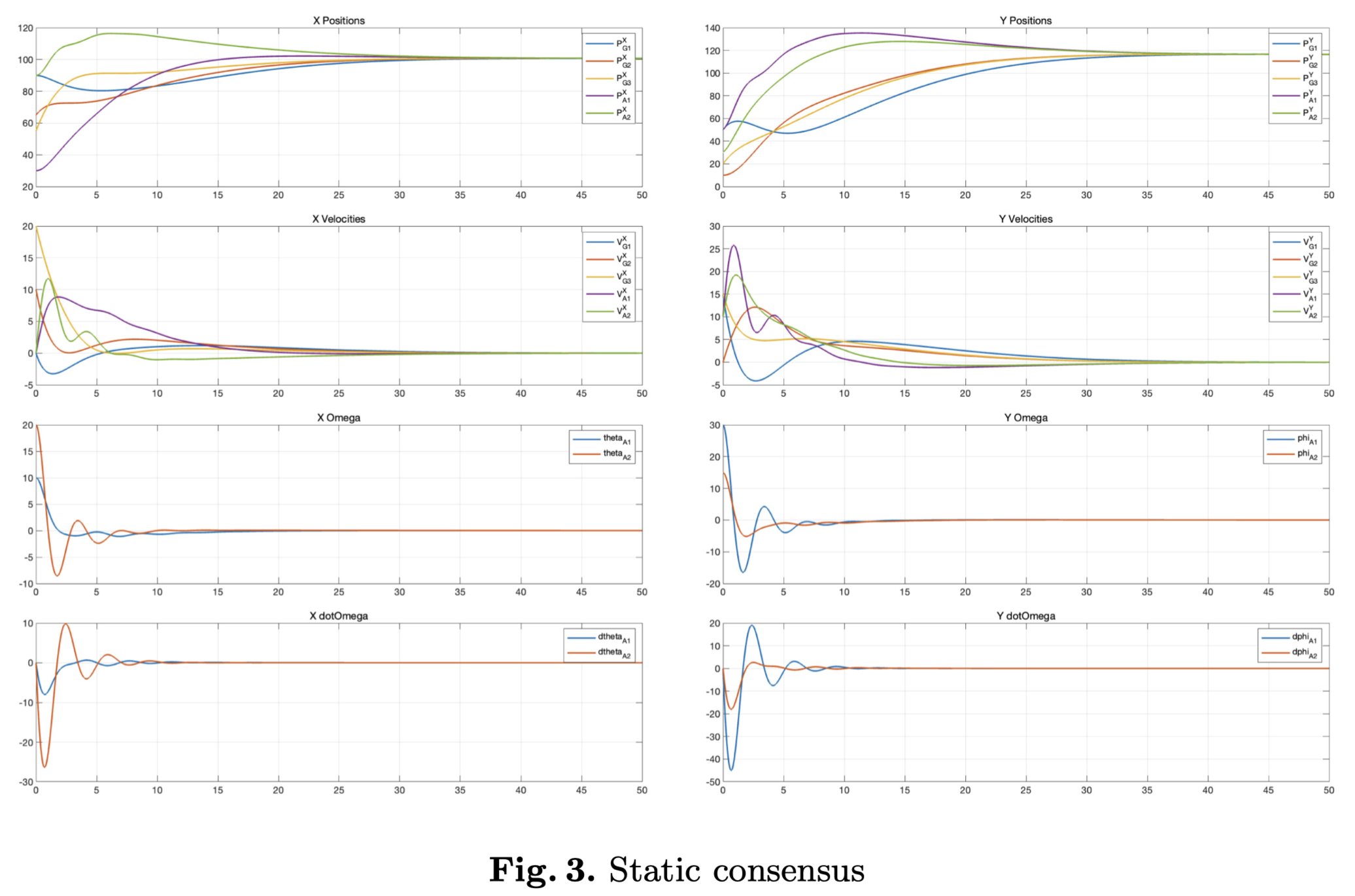
当使用静态一致性协议（14）时，系统的状态如图 3 所示。静态一致性的定义是位置达到一致，速度变为零。因此，当时间趋于无穷时，我们可以看到系统的速度变为0，而位置保持不变。
5 结论
本文以UGV为例，分析了二阶智能体的动力学模型；以UAV为例，分析了高阶智能体的动力学模型。通过Kronecker乘积，将两种不同阶数的智能体组合成一个混合阶异构多智能体系统。混合阶智能体的数量可以是任意数量。针对异构多智能体系统提出了两种共识协议，包括动态一致性和静态一致性。分析了一致性协议融合后系统的稳定性。该协议通过数值模拟进行了验证。
至于未来的工作，我们打算致力于研究异构多智能体系统合作架构下的异常检测和识别问题。当然，还将增加无人机在高度方向的控制，这将扩大该系统的空中工作范围。
程序代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158% UGV/UAV 异构控制一致性控制 % Author: Zhao-Jichao % Date: 2021-05-14 clear clc %% Laplacian Matrix L = [2 -1 -1 0 0 -1 3 -1 -1 0 -1 -1 3 0 -1 0 -1 0 2 -1 0 0 -1 -1 2]; %% Initial States % PositionX, PositionY, VeloctiyX, VelocityY (4) % UGV1 = [90, 50, 10, 10]'; % UGV2 = [65, 10, 10, 10]'; % UGV3 = [55, 20, 10, 10]'; % PositionX, PositionY, PositionZ, VeloctiyX, VelocityY, VelocityZ, % Pitch, Phi, Psi, dPitch, dPhi, dPsi (12) % UAV4 = [25, 10, 10, 10, 10, 00, 10, 10, 00, 10, 10, 00]'; % UAV5 = [10, 30, 10, 10, 10, 00, 10, 10, 00, 10, 10, 00]'; % X0 = [UGV1; UGV2; UGV3; UAV4; UAV5]; P1X(1,1) = 90; P1Y(1,1) = 50; V1X(1,1) = 0; V1Y(1,1) = 15; P2X(1,1) = 65; P2Y(1,1) = 10; V2X(1,1) = 10; V2Y(1,1) = 0; P3X(1,1) = 55; P3Y(1,1) = 20; V3X(1,1) = 20; V3Y(1,1) = 15; P4X(1,1) = 30; P4Y(1,1) = 50; P4Z(1,1) = 50; V4X(1,1) = 00; V4Y(1,1) = 10; V4Z(1,1) = 0; gtheta4(1,1) = 10; gphi4(1,1) = 30; gpsi4(1,1) = 0; gdtheta4(1,1) = 00; gdphi4(1,1) = 00; gdpsi4(1,1) = 0; P5X(1,1) = 90; P5Y(1,1) = 30; P5Z(1,1) = 50; V5X(1,1) = 00; V5Y(1,1) = 10; V5Z(1,1) = 0; gtheta5(1,1) = 20; gphi5(1,1) = 15; gpsi5(1,1) = 00; gdtheta5(1,1) = 00; gdphi5(1,1) = 00; gdpsi5(1,1) = 00; % Time parameters tBegin = 0; tFinal = 50; dT = 0.01; times = (tFinal-tBegin)/dT; time(1,1) = 0; %% Calculate r1 = 0.1; r2 = 0.8; r3 = 4.0; r4 = 1.5; global protocol protocol = 1; % (1:Dynamic/2:Static) for i=1:times time(i+1,1) = time(i,1) + dT; if protocol == 1 u1x = r1*( (P2X(i,:)-P1X(i,:))+(P3X(i,:)-P1X(i,:)) ) + r2*( (V2X(i,:)-V1X(i,:))+(V3X(i,:)-V1X(i,:)) ); u2x = r1*( (P1X(i,:)-P2X(i,:))+(P3X(i,:)-P2X(i,:)+(P4X(i,:)-P2X(i,:))) ) + r2*( (V1X(i,:)-V2X(i,:))+(V3X(i,:)-V2X(i,:))+(V4X(i,:)-V2X(i,:)) ); u3x = r1*( (P1X(i,:)-P3X(i,:))+(P2X(i,:)-P3X(i,:)+(P5X(i,:)-P3X(i,:))) ) + r2*( (V1X(i,:)-V3X(i,:))+(V2X(i,:)-V3X(i,:))+(V5X(i,:)-V3X(i,:)) ); u4x = r1*( (P2X(i,:)-P4X(i,:))+(P5X(i,:)-P4X(i,:)) ) + r2*( (V2X(i,:)-V4X(i,:))+(V5X(i,:)-V4X(i,:)) ) + r3*( -gtheta4(i,:)) + r4*( -gdtheta4(i,:)); u5x = r1*( (P3X(i,:)-P5X(i,:))+(P4X(i,:)-P5X(i,:)) ) + r2*( (V3X(i,:)-V5X(i,:))+(V4X(i,:)-V5X(i,:)) ) + r3*( -gtheta5(i,:)) + r4*( -gdtheta5(i,:)); u1y = r1*( (P2Y(i,:)-P1Y(i,:))+(P3Y(i,:)-P1Y(i,:)) ) + r2*( (V2Y(i,:)-V1Y(i,:))+(V3Y(i,:)-V1Y(i,:)) ); u2y = r1*( (P1Y(i,:)-P2Y(i,:))+(P3Y(i,:)-P2Y(i,:)+(P4Y(i,:)-P2Y(i,:))) ) + r2*( (V1Y(i,:)-V2Y(i,:))+(V3Y(i,:)-V2Y(i,:))+(V4Y(i,:)-V2Y(i,:)) ); u3y = r1*( (P1Y(i,:)-P3Y(i,:))+(P2Y(i,:)-P3Y(i,:)+(P5Y(i,:)-P3Y(i,:))) ) + r2*( (V1Y(i,:)-V3Y(i,:))+(V2Y(i,:)-V3Y(i,:))+(V5Y(i,:)-V3Y(i,:)) ); u4y = r1*( (P2Y(i,:)-P4Y(i,:))+(P5Y(i,:)-P4Y(i,:)) ) + r2*( (V2Y(i,:)-V4Y(i,:))+(V5Y(i,:)-V4Y(i,:)) ) + r3*( -gphi4(i,:)) + r4*( -gdphi4(i,:)); u5y = r1*( (P3Y(i,:)-P5Y(i,:))+(P4Y(i,:)-P5Y(i,:)) ) + r2*( (V3Y(i,:)-V5Y(i,:))+(V4Y(i,:)-V5Y(i,:)) ) + r3*( -gphi5(i,:)) + r4*( -gdphi5(i,:)); end if protocol == 2 u1x = r1*( (P2X(i,:)-P1X(i,:))+(P3X(i,:)-P1X(i,:)) ) + r2*( -V1X(i,:) ); u2x = r1*( (P1X(i,:)-P2X(i,:))+(P3X(i,:)-P2X(i,:)+(P4X(i,:)-P2X(i,:))) ) + r2*( -V2X(i,:) ); u3x = r1*( (P1X(i,:)-P3X(i,:))+(P2X(i,:)-P3X(i,:)+(P5X(i,:)-P3X(i,:))) ) + r2*( -V3X(i,:) ); u4x = r1*( (P2X(i,:)-P4X(i,:))+(P5X(i,:)-P4X(i,:)) ) + r2*( (V2X(i,:)-V4X(i,:))+(V5X(i,:)-V4X(i,:)) ) + r3*( -gtheta4(i,:)) + r4*( -gdtheta4(i,:)); u5x = r1*( (P3X(i,:)-P5X(i,:))+(P4X(i,:)-P5X(i,:)) ) + r2*( (V3X(i,:)-V5X(i,:))+(V4X(i,:)-V5X(i,:)) ) + r3*( -gtheta5(i,:)) + r4*( -gdtheta5(i,:)); u1y = r1*( (P2Y(i,:)-P1Y(i,:))+(P3Y(i,:)-P1Y(i,:)) ) + r2*( -V1Y(i,:) ); u2y = r1*( (P1Y(i,:)-P2Y(i,:))+(P3Y(i,:)-P2Y(i,:)+(P4Y(i,:)-P2Y(i,:))) ) + r2*( -V2Y(i,:) ); u3y = r1*( (P1Y(i,:)-P3Y(i,:))+(P2Y(i,:)-P3Y(i,:)+(P5Y(i,:)-P3Y(i,:))) ) + r2*( -V3Y(i,:) ); u4y = r1*( (P2Y(i,:)-P4Y(i,:))+(P5Y(i,:)-P4Y(i,:)) ) + r2*( (V2Y(i,:)-V4Y(i,:))+(V5Y(i,:)-V4Y(i,:)) ) + r3*( -gphi4(i,:)) + r4*( -gdphi4(i,:)); u5y = r1*( (P3Y(i,:)-P5Y(i,:))+(P4Y(i,:)-P5Y(i,:)) ) + r2*( (V3Y(i,:)-V5Y(i,:))+(V4Y(i,:)-V5Y(i,:)) ) + r3*( -gphi5(i,:)) + r4*( -gdphi5(i,:)); end V1X(i+1,1) = V1X(i,1)+dT*u1x; P1X(i+1,1) = P1X(i,1)+dT*V1X(i+1,1); V2X(i+1,1) = V2X(i,1)+dT*u2x; P2X(i+1,1) = P2X(i,1)+dT*V2X(i+1,1); V3X(i+1,1) = V3X(i,1)+dT*u3x; P3X(i+1,1) = P3X(i,1)+dT*V3X(i+1,1); gdtheta4(i+1,1) = gdtheta4(i,1)+dT*u4x; gtheta4(i+1,1) = gtheta4(i,1)+dT*gdtheta4(i+1,1); V4X(i+1,1) = V4X(i,1)+dT*gtheta4(i+1,1); P4X(i+1,1) = P4X(i,1)+dT*V4X(i+1,1); gdtheta5(i+1,1) = gdtheta5(i,1)+dT*u5x; gtheta5(i+1,1) = gtheta5(i,1)+dT*gdtheta5(i+1,1); V5X(i+1,1) = V5X(i,1)+dT*gtheta5(i+1,1); P5X(i+1,1) = P5X(i,1)+dT*V5X(i+1,1); V1Y(i+1,1) = V1Y(i,1)+dT*u1y; P1Y(i+1,1) = P1Y(i,1)+dT*V1Y(i+1,1); V2Y(i+1,1) = V2Y(i,1)+dT*u2y; P2Y(i+1,1) = P2Y(i,1)+dT*V2Y(i+1,1); V3Y(i+1,1) = V3Y(i,1)+dT*u3y; P3Y(i+1,1) = P3Y(i,1)+dT*V3Y(i+1,1); gdphi4(i+1,1) = gdphi4(i,1)+dT*u4y; gphi4(i+1,1) = gphi4(i,1)+dT*gdphi4(i+1,1); V4Y(i+1,1) = V4Y(i,1)+dT*gphi4(i+1,1); P4Y(i+1,1) = P4Y(i,1)+dT*V4Y(i+1,1); gdphi5(i+1,1) = gdphi5(i,1)+dT*u5y; gphi5(i+1,1) = gphi5(i,1)+dT*gdphi5(i+1,1); V5Y(i+1,1) = V5Y(i,1)+dT*gphi5(i+1,1); P5Y(i+1,1) = P5Y(i,1)+dT*V5Y(i+1,1); end %% Draw graphs subplot(4,2,1, 'Position',[0.02 0.775 0.45 0.20]) plot(time,P1X, time,P2X, time,P3X, time,P4X, time,P5X, 'linewidth',1.5); legend('P^X_{G1}','P^X_{G2}','P^X_{G3}','P^X_{A1}','P^X_{A2}'); grid on title("X Positions") subplot(4,2,3, 'Position',[0.02 0.525 0.45 0.20]) plot(time,V1X, time,V2X, time,V3X, time,V4X, time,V5X, 'linewidth',1.5); legend('V^X_{G1}','V^X_{G2}','V^X_{G3}','V^X_{A1}','V^X_{A2}'); grid on title("X Velocities") subplot(4,2,5, 'Position',[0.02 0.275 0.45 0.20]) plot(time,gtheta4, time,gtheta5, 'linewidth',1.5); legend('theta_{A1}','theta_{A2}'); grid on title("X Omega") subplot(4,2,7, 'Position',[0.02 0.025 0.45 0.20]) plot(time,gdtheta4, time,gdtheta5, 'linewidth',1.5); legend('dtheta_{A1}','dtheta_{A2}'); grid on title("X dotOmega") subplot(4,2,2, 'Position',[0.53 0.775 0.45 0.20]) plot(time,P1Y, time,P2Y, time,P3Y, time,P4Y, time,P5Y, 'linewidth',1.5); legend('P^Y_{G1}','P^Y_{G2}','P^Y_{G3}','P^Y_{A1}','P^Y_{A2}'); grid on title("Y Positions") subplot(4,2,4, 'Position',[0.53 0.525 0.45 0.20]) plot(time,V1Y, time,V2Y, time,V3Y, time,V4Y, time,V5Y, 'linewidth',1.5); legend('V^Y_{G1}','V^Y_{G2}','V^Y_{G3}','V^Y_{A1}','V^Y_{A2}'); grid on title("Y Velocities") subplot(4,2,6, 'Position',[0.53 0.275 0.45 0.20]) plot(time,gphi4, time,gphi5, 'linewidth',1.5); legend('phi_{A1}','phi_{A2}'); grid on title("Y Omega") subplot(4,2,8, 'Position',[0.53 0.025 0.45 0.20]) plot(time,gdphi4, time,gdphi5, 'linewidth',1.5); legend('dphi_{A1}','dphi_{A2}'); grid on title("Y dotOmega")
最后
以上就是自信信封最近收集整理的关于【Paper】2021_使用UGV和UAV的异构混合阶多智能体系统一致性摘要1 介绍2 预备知识3 主要结果4 仿真5 结论程序代码的全部内容，更多相关【Paper】2021_使用UGV和UAV的异构混合阶多智能体系统一致性摘要1内容请搜索靠谱客的其他文章。
发表评论 取消回复