MATLAB混沌非线性,一个非线性系统的混沌现象分析及数值仿真

1. 引言

对非线性系统的探索和研究已持续一个多世纪的时间，但仍然方兴未艾。20世纪70年代初，科学家们利用计算机和非线性数学，发现了非线性系统中的混沌行为，这一发现极大地激起了人们对复杂问题探索的热情，对混沌的研究热潮也开始了。混沌现象的研究对现代科学的影响是广泛的，几乎涉及到了任何领域。

1963年，气象学家E.N. Lorenz在数值实验中发现了混沌现象，提出了Lorenz系统 [1]，自此，不管是国际上还是国内，人们不断地提出和构建新的混沌系统。很多的学术专家都曾展示了自己的研究成果，在国内有影响力的像Chen-系统 [2] [3]，Lv-系统 [4] 等等，在2004年，刘崇新教授等人又提出了Liu-系统 [5]。Liu-混沌系统属于广义Lorenz系统，Chen-系统与Lorenz系统互为对偶系统，而Lv-系统在Lorenz系统和Chen系统之间架起了桥梁，四者之间的联系十分紧密。本文在Liu-系统的基础上，研究了一个新的非线性系统 [6]，对其动力学行为进行了数值仿真，因而初步分析了其混沌行为 [7] [8] [9]。

2. 数学模型

2.1. 系统描述

根据文献 [6] 所提到的一类新的混沌系统：

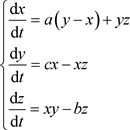(1)

其中状态变量

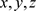均为时间t的函数，

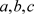为控制参数。

2.2. 对称性与不变性

对于系统(1)，通过变化

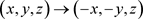对系统(1)进行处理，发现系统的控制参数

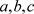不发生变动。对应的非线性系统(1)也保持它的原有属性，而且仍然以z轴为对称轴。系统(1)具有对称性和不变性。

2.3. 系统耗散性与吸引子不变性

对于系统(1)，作如下处理：

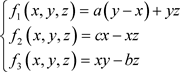(2)

则系统(1)的散度为：

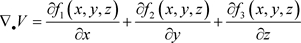(3)

当

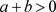时，系统(1)是耗散的，故存在吸引子，即

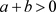是吸引子存在的条件。

2.4. 平衡点及局部稳定性

对于系统(1)中的各式，令其方程右边等于0，可以解得系统(1)的三个平衡点 [10]，分别为：

，

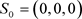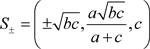
其中

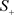和

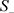对称的落在 轴的两侧，对于

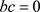，系统(1)有唯一的平衡点

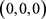。下面讨论各平衡点的稳定性。

在平衡点

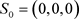处通过线性变换处理后，得到Jacobian矩阵为：

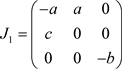
其对应的特征方程为：

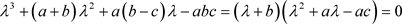(4)

解得上述Jacobian矩阵的三个特征值分别为：

,

,

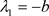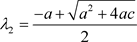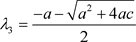
当

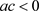时，

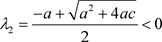，故系统存在三个负实根，此时平衡点

稳定。为了直观地判

断平衡点稳定与否，我们不妨设

，

，

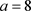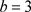，此时三个特征值分别为−3，6.95，−14.95，存在一个大于0的特征值，由Routh-Hurwitz原理可知，平衡点

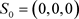是不稳定的。

对于平衡点

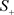和

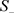，由于系统(1)通过变化

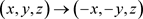后，系统的控制参数

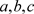不发生变动。对应的非线性系统(1)也保持它的原有属性，而且P+和P−也关于 轴对称，所以二者性质相同，这里不妨只分析

。

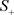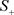对应的Jacobian矩阵为：

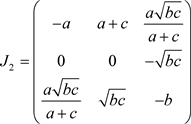
其特征方程为：

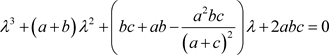(5)

根据Routh-Hurwitz原理以及参数

的取值范围，可知该特征方程仅有实部为负的根，故

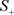为不稳定的平衡点，同理，

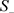也为不稳定的平衡点。

3. 数值仿真

本节对系统(1)的动力学行为进行数值仿真。当固定两个系统参数时，随着参数a的增大，系统的动力学行为发生了一系列的变化。采用龙格–库塔方法编写MATLAB程序，画出仿真图，并揭示系统(1)的混沌学行为 [11]。

当固定参数

，

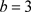时，图1和图2分别给出了

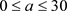时的分岔图与最大Lyapunov指数，图3为当

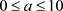时局部放大的分岔图，图4和图5分别为

，

，

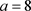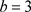时的吸引子图和庞家莱截面图，图6为

，

，

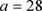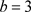时的吸引子图。

系统经过一系列复杂演变过程，经Hopf分岔到达混沌态，当

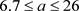时，系统彻底发生混沌，当

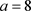时，混沌现象已经出现，当

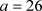时，混沌结束，系统进入周期轨道。

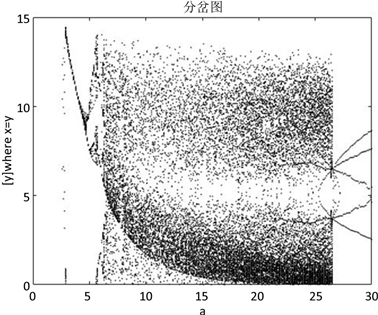
Figure 1. Bifurcation diagram when 0 ≤ a ≤ 30, b = 3, c = 13

图1. 0 ≤ a ≤ 30，b = 3，c = 13时的分岔图

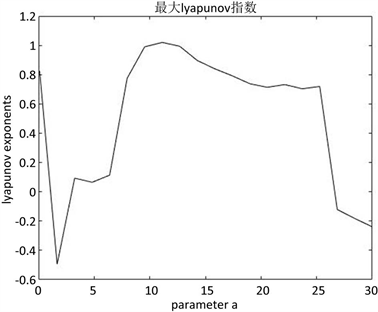
Figure 2. Graph of maximum Lyapunov index when 0 ≤ a ≤ 30, b = 3, c = 13

图2. 0 ≤ a ≤ 30，b = 3，c = 13时的最大Lyapunov指数图

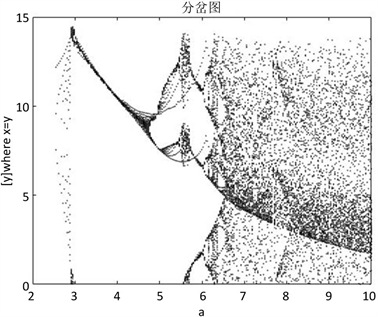
Figure 3. Bifurcation diagram when 0 ≤ a ≤ 10, b = 3, c = 13

图3. 0 ≤ a ≤ 10，b = 3，c = 13时的分岔图

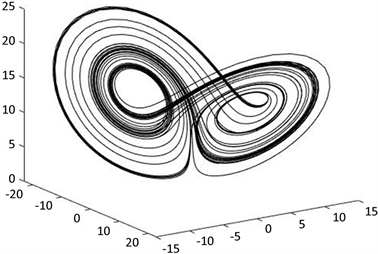
Figure 4. Attractor graph when a = 8, b = 3, c = 13

图4. a = 8，b = 3，c = 13时的吸引子图

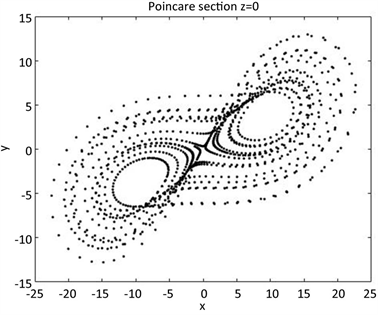
Figure 5. Panjialai Section when a = 8, b = 3, c = 13

图5. a = 8，b = 3，c = 13时的庞家莱截面图

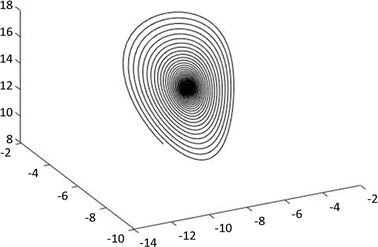
Figure 6. Attractor graph when a = 28, b = 3, c = 13

图6. a = 28，b = 3，c = 13时的吸引子图

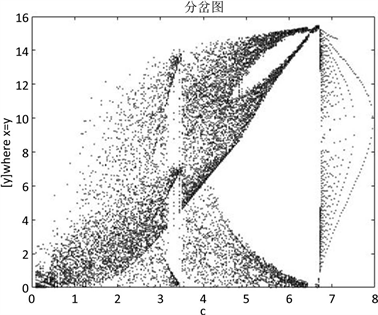
Figure 7. Bifurcation diagram when 0 ≤ b ≤ 10, b = 3, c = 13

图7. 0 ≤ b ≤ 10，b = 3，c = 13时的分岔图

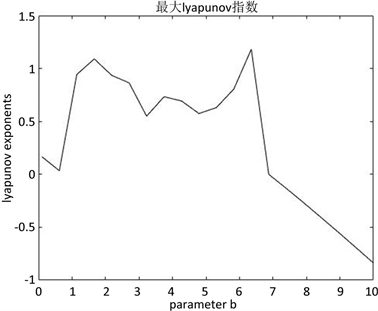
Figure 8. Graph of maximum Lyapunov index when 0 ≤ b ≤ 10, b = 3, c = 13

图8. 0 ≤ b ≤ 10，b = 3，c = 13时的最大Lyapunov指数图

当固定参数

，

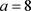时，图7和图8分别给出了

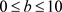时的分岔图和最大Lyapunov指数图。当

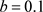时混沌出现，当

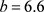时混沌逐渐消失，其中有一个较为明显的周期窗口。

当固定参数

，

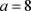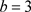时，图9和图10分别给出当

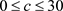时的分岔图和最大Lyapunov指数图。

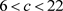时，系统处于混沌状态，其中存在一个明显的周期窗口。

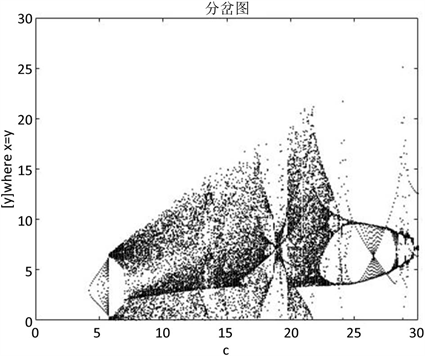
Figure 9. Bifurcation diagram when a = 8, b = 3, 0 ≤ c ≤ 30

图9. a = 8，b = 3，0 ≤ c ≤ 30时的分岔图

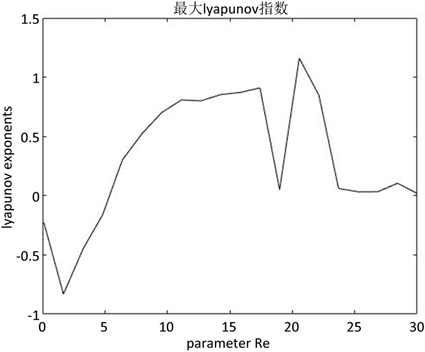
Figure 10. Graph of maximum Lyapunov index when a = 8, b = 3, 0 ≤ c ≤ 30

图10. a = 8，b = 3，0 ≤ c ≤ 30时的最大Lyapunov指数图

综合以上三个系统参数使系统发生混沌的范围，不妨取

，

，

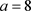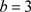进行数值仿真。图11、图12和图13分别为该组参数下的返回映射、时间序列和功率谱，从中可以看出此时系统正处于混沌状态下。

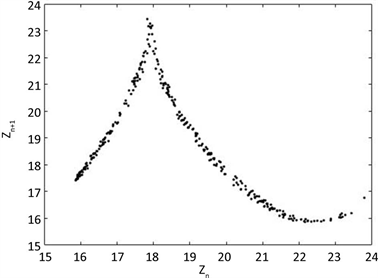
Figure 11. Return map when a = 8, b = 3, c = 13

图11. a = 8，b = 3，c = 13时的返回映射

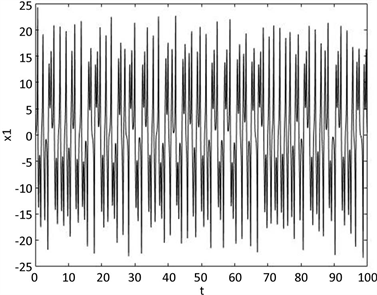
Figure 12. Time series when a = 8, b = 3, c = 13

图12. a = 8，b = 3，c = 13时的时间序列

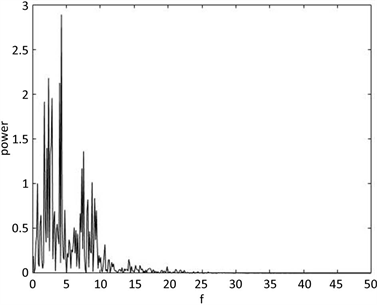
Figure 13. Power Spectrum when a = 8, b = 3, c = 13

图13. a = 8，b = 3，c = 13时的功率谱

4. 结论

本文首先对所研究的内容研究现状及近期发展进行简介；其次，说明系统的对称性与不变性，讨论系统的耗散性与吸引子的存在性，计算平衡点及证明其局部稳定性，说明系统确实存在混沌；最后对系统的三个参数

分别进行数值仿真，确定混沌产生的区间，并选取一组参数值：

，

，

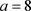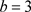，仿真出吸引子图、庞家莱映射图、时间序列、返回映射和功率谱，充分证明在此参数值下，系统正在发生混沌。