智能车跟随圆弧路径原理
1. 圆弧点生成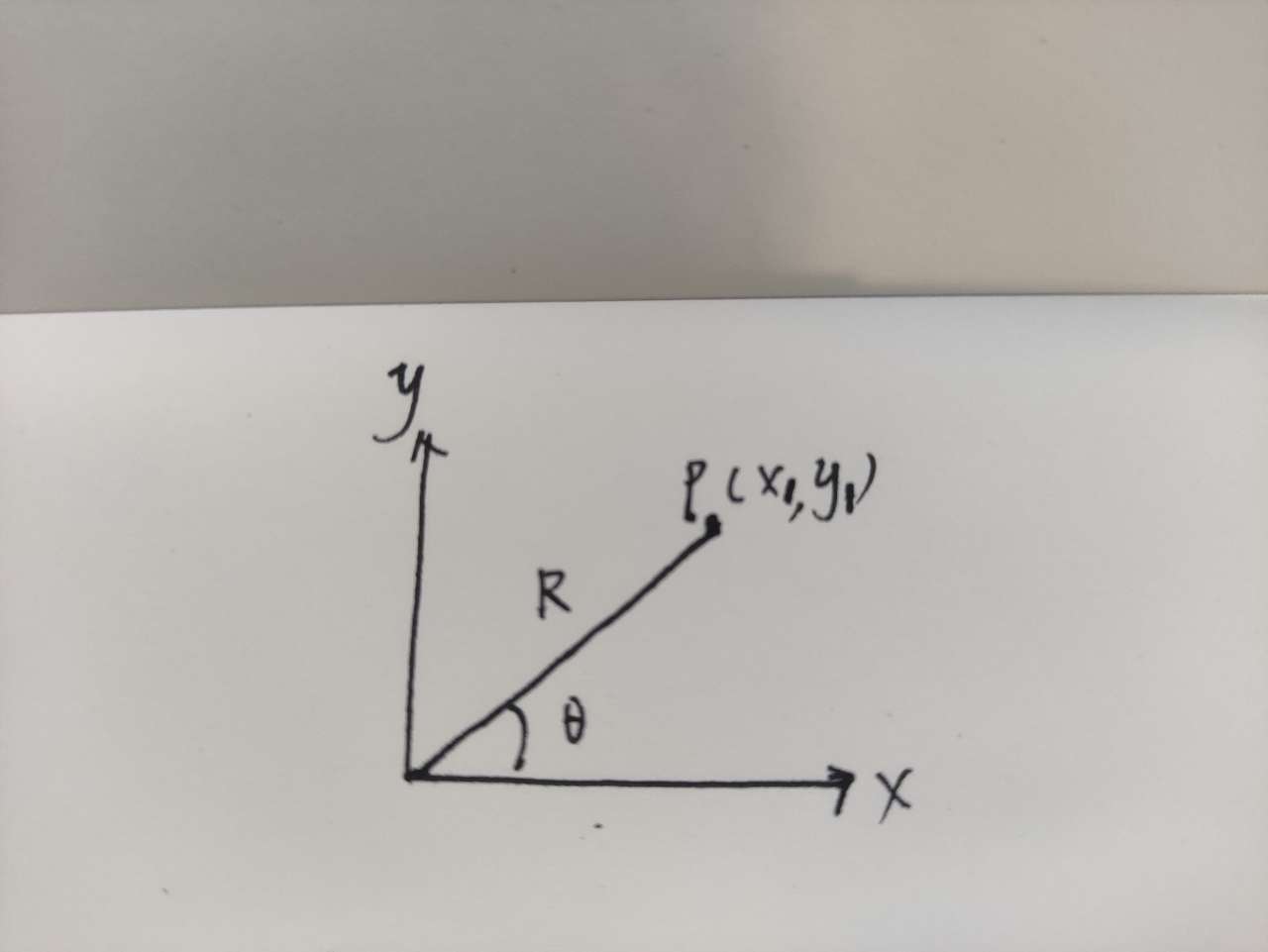
2. 圆弧点的公式
x
=
R
c
o
s
θ
y
=
R
s
i
n
θ
(1)
begin{aligned} x = Rcostheta \ y = Rsintheta tag{1} end{aligned}
x=Rcosθy=Rsinθ(1)
通过对点的求导,可以得到点在世界坐标系下的速度关系
x
˙
=
−
R
s
i
n
θ
θ
˙
y
˙
=
R
c
o
s
θ
θ
˙
(2)
begin{aligned} dot x &= -Rsinthetadottheta \ dot y &= Rcosthetadottheta \ tag{2} end{aligned}
x˙y˙=−Rsinθθ˙=Rcosθθ˙(2)
通过**公式(1)(2)**得到每个时刻小车在
X
,
Y
X, Y
X,Y轴的速度值,将速度传给麦克纳姆轮的运动学模型即可进
行圆弧运动,小车的角速度为
0
0
0。 本文麦克纳姆轮小车车头朝向跟机器人坐标系Y轴方向一致
思路流程
得
到
圆
弧
的
点
的
坐
标
→
求
导
→
得
到
每
个
点
的
瞬
时
速
度
关
系
(
x
˙
,
y
˙
,
0
)
→
麦
克
纳
姆
轮
运
动
学
模
型
→
四
个
电
机
得到圆弧的点的坐标rightarrow求导rightarrow得到每个点的瞬时速度关系(dot x, dot y, 0)rightarrow麦克纳姆轮运动学模型rightarrow四个电机
得到圆弧的点的坐标→求导→得到每个点的瞬时速度关系(x˙,y˙,0)→麦克纳姆轮运动学模型→四个电机
通过上述流程得到,麦克纳姆轮成功走出圆的轨迹,但是车头方向是固定不变的。
接着,如何让小车走圆轨迹的时候,小车的车头跟圆的速度切线方向一致 或者 小车车头一直指向世界坐标系的原点(即圆弧的圆心) 呢
3. 圆弧路径跟随进阶
3.1 小车车头与圆的速度切线方向一致
此时的麦克纳姆轮小车可以简化成为两轮差速小车模型,有关两轮差速小车走圆的资料挺多的。也可以借鉴一下阿克曼构型的纯追踪算法如何跟踪圆弧轨迹。
接下来本文用另一种思路去解释,需要用到旋转变换的思想。 当然可以自己尝试对圆进行运动学分析,得到结果也会一样。
x
′
,
y
′
表
示
的
是
机
器
人
坐
标
系
,
x
,
y
表
示
的
是
世
界
坐
标
系
。
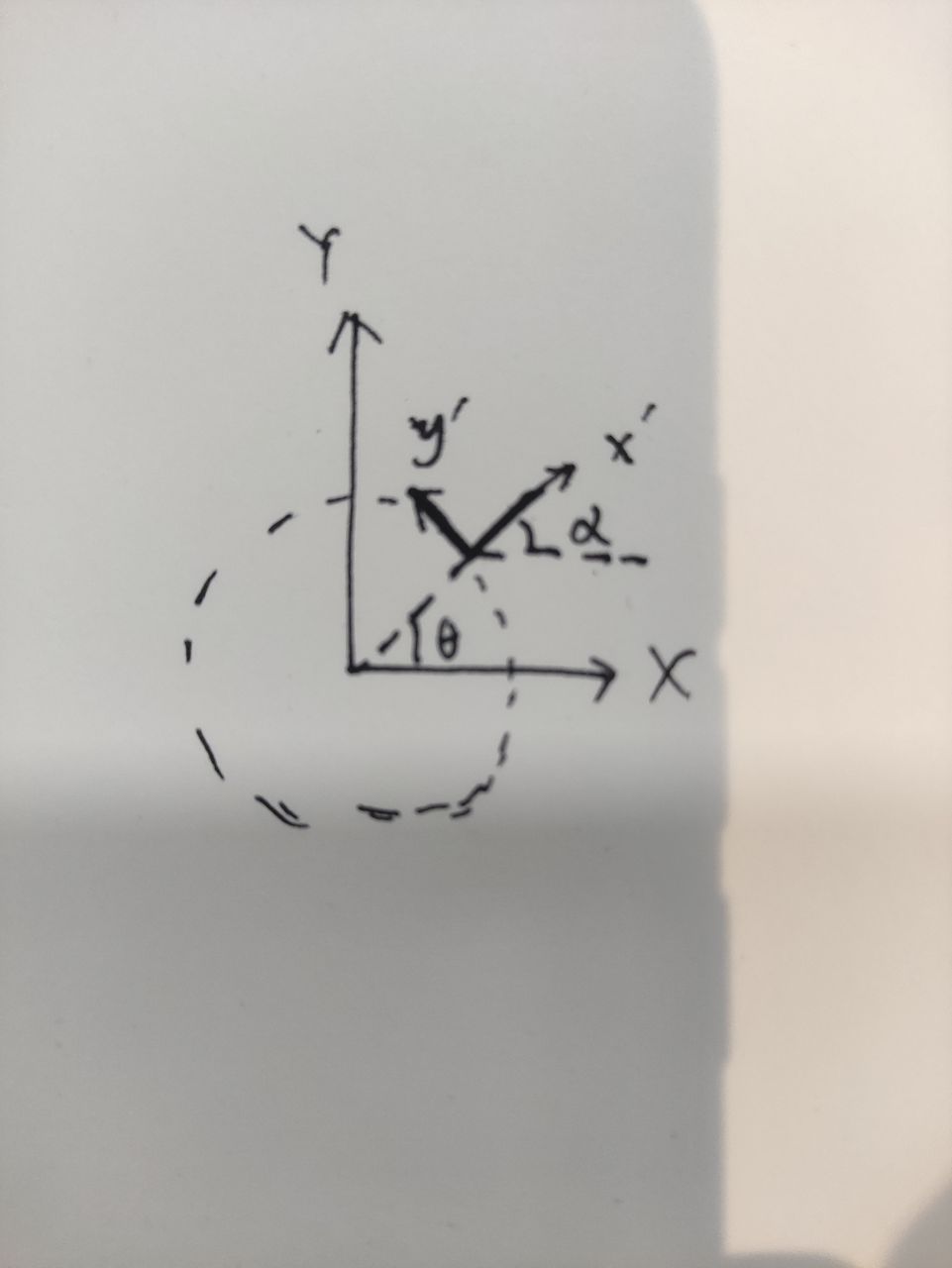
x^{'}, y^{'}表示的是机器人坐标系, x, y 表示的是世界坐标系。
x′,y′表示的是机器人坐标系,x,y表示的是世界坐标系。
当机器人车头方向与速度方向一致的时候
α
=
θ
alpha = theta
α=θ
第一种情况,因为机器人车头朝向是固定不变的,且机器人的坐标系方向与世界坐标系方向一致,因此瞬时速度在世界坐标系和机器人坐标系中都是一致(大小,方向)的。
当前情况,由于机器人坐标系与世界坐标系是存在角度
α
alpha
α,我们得到的公式(2)是世界坐标系下的瞬时速度,需要转换到机器人坐标系中,存在旋转矩阵
R
r
w
R_{rw}
Rrw.
w
是
世
界
坐
标
系
(
W
o
r
l
d
C
o
o
r
d
i
n
a
t
e
)
,
r
是
机
器
人
坐
标
系
(
R
o
b
o
t
C
o
o
r
d
i
n
a
t
e
)
w是世界坐标系(World Coordinate),r是机器人坐标系(Robot Coordinate)
w是世界坐标系(WorldCoordinate),r是机器人坐标系(RobotCoordinate).
通过旋转矩阵我们得知
R
a
b
∗
R
b
a
=
I
R
b
a
=
R
a
b
−
1
=
R
a
b
⊺
R_{ab} * R_{ba} = I \ R_{ba} = R^{-1}_{ab} = {R_{ab}}^intercal
Rab∗Rba=IRba=Rab−1=Rab⊺
R
a
b
=
[
c
o
s
α
−
s
i
n
α
s
i
n
α
c
o
s
α
]
R_{ab} =left[ begin{matrix} cosalpha & -sinalpha \ sinalpha & cosalpha \ end{matrix} right]
Rab=[cosαsinα−sinαcosα]
因此
R
r
w
=
[
c
o
s
α
s
i
n
α
−
s
i
n
α
c
o
s
α
]
R_{rw} =left[ begin{matrix} cosalpha & sinalpha \ -sinalpha & cosalpha \ end{matrix} right]
Rrw=[cosα−sinαsinαcosα]
把世界坐标系的瞬时速度通过旋转变换到机器人坐标系下,即可得到机器人需要运行的速度
(
x
˙
r
,
y
˙
r
,
θ
˙
r
)
(dot x_r, dot y_r, dot theta_r)
(x˙r,y˙r,θ˙r)
V
r
=
R
r
w
V
w
[
x
˙
r
y
˙
r
]
=
[
c
o
s
α
s
i
n
α
−
s
i
n
α
c
o
s
α
]
∗
[
x
˙
y
˙
]
V_r = R_{rw}V_w \ left[ begin{matrix} dot x_r \ dot y_r \ end{matrix} right] = left[ begin{matrix} cosalpha & sinalpha \ -sinalpha & cosalpha \ end{matrix} right] * left[ begin{matrix} dot x \ dot y \ end{matrix} right]
Vr=RrwVw[x˙ry˙r]=[cosα−sinαsinαcosα]∗[x˙y˙]
因为小车要走圆弧,因此角速度跟世界坐标系下的角速度一致,最后通过整理得到:
x
˙
r
=
−
R
s
i
n
(
θ
−
α
)
θ
˙
y
˙
r
=
R
c
o
s
(
θ
−
α
)
θ
˙
θ
˙
r
=
θ
˙
begin{aligned} dot x_r &= -Rsin(theta -alpha)dot theta\ dot y_r &= Rcos(theta-alpha)dot theta\ dot theta_r &= dottheta end{aligned}
x˙ry˙rθ˙r=−Rsin(θ−α)θ˙=Rcos(θ−α)θ˙=θ˙
最后将速度
(
x
˙
r
,
y
˙
r
,
θ
˙
r
)
(dot x_r,dot y_r,dot theta_r )
(x˙r,y˙r,θ˙r)传递到麦卡纳姆轮运动学模型中,即可完成车头跟速度切向方向一致的绕圆弧运动。
同理,对于小车车头一直指向世界坐标系的原点(即圆弧的圆心)也是旋转变换。
因
此
当
α
和
θ
角
度
关
系
的
不
同
,
小
车
绕
圆
弧
运
动
也
不
一
样
,
如
下
图
所
示
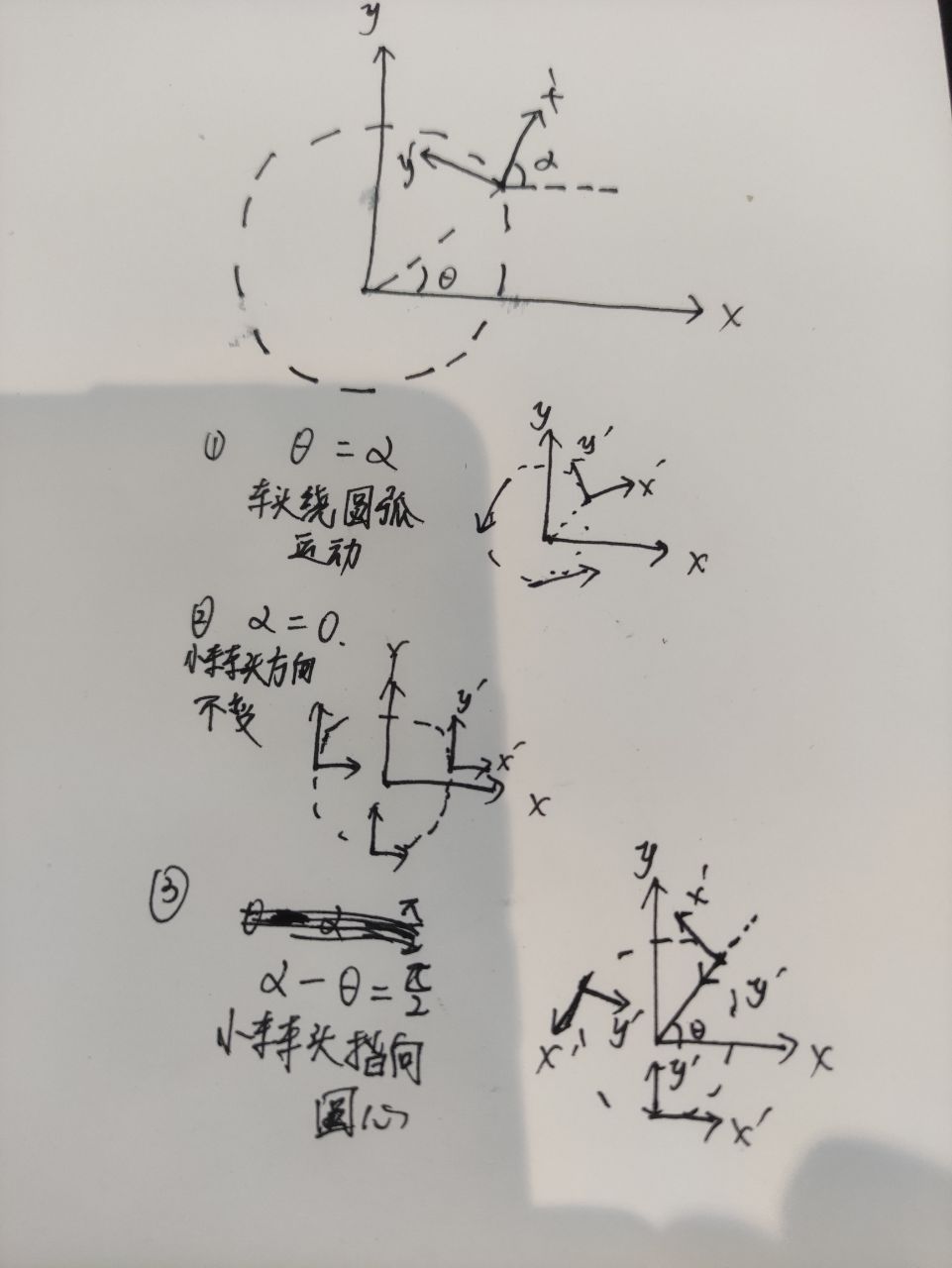
因此当alpha和theta角度关系的不同,小车绕圆弧运动也不一样,如下图所示
因此当α和θ角度关系的不同,小车绕圆弧运动也不一样,如下图所示
4. 个人思考与反思
1.在得到机器人走圆弧轨迹的方程后,如何让机器人进行一定时间内的速度规划?也就是轨迹规划,如三次、五次、梯形、S型规划,可以在评论区留言,后续会更新轨迹规划章节。
最后
以上就是风趣鸵鸟最近收集整理的关于智能车跟随圆弧路径原理的全部内容,更多相关智能车跟随圆弧路径原理内容请搜索靠谱客的其他文章。








发表评论 取消回复