简介
Ziegler—Nichols(Z—N)的PID整定方法在工程快速 计算方面具有很大的影响力,它的频率响应方法是通 过PID控制器的临界振荡试验获得被控对象重要的临界频率响应特性,并根据经验给出相应的PID参数经 验公式。Z—N整定方法的优点在于在计算过程中不需要另外建立任何对象控制模型,简单实用,所以目前该 方法在自动控制领域中仍被广泛采用。
Z-N调谐表
齐格勒-尼科尔斯规则是第一个提供一个的实用方法来调整PID控制器。根据该规则,一个PID控制器的调谐方法是首先将其设置为纯P模式,然后调整增益,使控制系统处于连续振荡状态。相应的增益被称为终极增益(Ku),振荡周期为振荡周期被称为终极周期(Pu)。然后,PID控制器的参数由Ku和Pu决定,使用的Ziegler-Nichols调谐表

代码原理
确定最终增益和周期Ziegler-Nichols调谐方法的关键步骤是确定的极限增益和周期。然而,通过实验来确定最终的增益和周期是很费时间的。由于连续振荡模式与临界稳定条件相对应,对于线性系统。这样的条件可以很容易地通过稳定性余量来确定。 其他工具,如Routh准则和Evans根基位置,不能直接处理延时问题。 让系统在分频器频率Wcg时有增益余量Gm。这相当于与一个单位增益控制器连接。因此,如果控制器的增益增加Gm,那么系统将在的频率Wcg振荡。
H为minreal函数用来消除控制系统中的零极点因子,具体使用方法大家可以参数这篇博客
matlab-自控原理 minreal 消除相同的零极点因子
margin函数用于求取系统传递函数的幅值裕度、相位裕度、截止频率,具体使用方法大家可参考
matlab-自控原理 margim求取函数幅值、相位裕度以及截止频率
具体代码
% ❥(^_-)Missing Alun every moment ❤
clear all;
clc;
T=100;
dt=3;
G=tf([4 5] ,[1 310 2]);
G.InputDelay=dt;
[k,ku,pu]=znpidtuning(G,3);
step(feedback(ss(G*ku),10),5*pu)
C=k.kc*(1+tf(1,[k.ti 0]));
H=minreal(feedback(ss(G*C),1));
step(10*H)
kc=0.2*T/(1*dt);
ti=3.33*dt;
C1=kc*(1+tf(1,[ti 0]));
H1=minreal(feedback(ss(G*C1),1));
hold
step(10*H1)
grid
legend('stability margin approach','process reaction curve appraoch')
function [k,ku,pu]=znpidtuning(g,ctype)
%k:结构化控制器参数
% ku:最终增益
% pu:最终期限
%输入检查
error(nargchk(1,2,nargin));
if ~isa(g,'lti')
error('The plant model is not a LTI object.')
end
%判断类型
if nargin<2
ctype=2;
end
[Gm,Pm,Wcg]=margin(g);
% gm——赋值裕度
% pm——相位裕度
% wcg——赋值穿越频率(截止频率)
% wcp——相位穿越频率
% G——传递函数
% 如果我们增加Gm的增益,系统就会非常稳定。因此的最终增益,以分贝为单位,等于增益幅度,即:
ku=Gm;
pu=2*pi/Wcg;
switch ctype
case 1 % P-controller
k.kc=ku/2;
case 2 % PI-controller
k.kc=ku/2.2;
k.ti=pu/1.2;
case 3 % PID-controller
k.kc=ku/1.7;
k.ti=pu/2;
k.td=pu/8;
end
测试结果
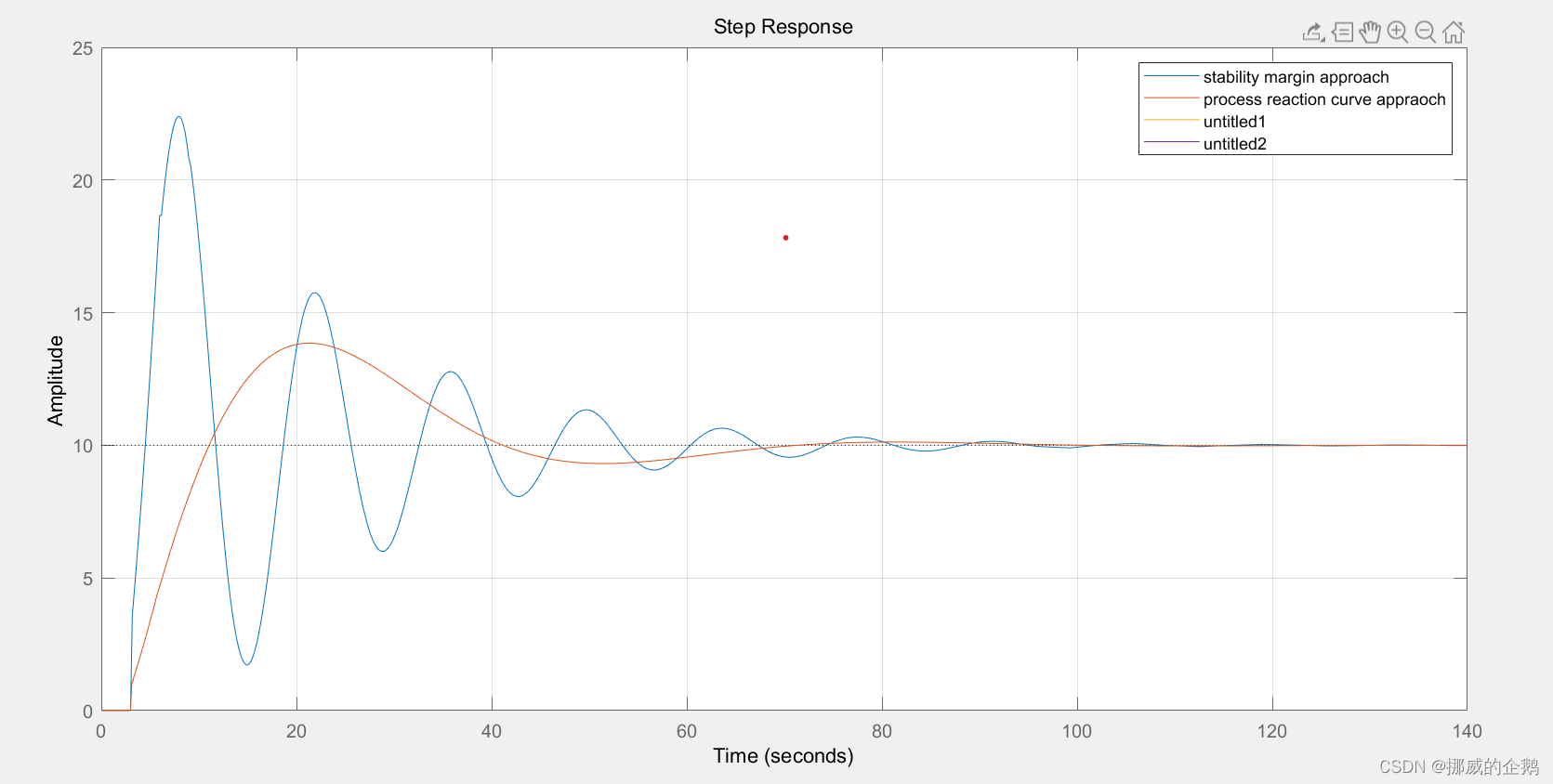
备注
大家可以根据自己的实际需要对传递函数参数进行修改,实测在常见一阶和二阶系统中都可以得到相对较好的结果 。Z-N法适合用于对系统PID参数进行初步估计,实际中要想得到较好的控制效果,还需对参数进行细调。
参考文献
[1].杨智,陈志堂,范正平,等. 基于改进粒子群优化算法的PID控制器整定[J]. 控制理论与应用,2010,27(10):1345-1352.
[2].郑艳秋,张英,尤恺,等. 基于相角裕度的PID控制器自整定改进算法的研究[J]. 核动力工程,2020,41(z2):108-113. DOI:10.13832/j.jnpe.2020.S2.0108.
最后
以上就是专一芒果最近收集整理的关于基于Matlab编辑器Z-N法整定PID参数Z-N调谐表代码原理具体代码测试结果备注参考文献的全部内容,更多相关基于Matlab编辑器Z-N法整定PID参数Z-N调谐表代码原理具体代码测试结果备注参考文献内容请搜索靠谱客的其他文章。







![[MATLAB调试笔记]Update magnetic field in one step](https://www.shuijiaxian.com/files_image/reation/bcimg12.png)
发表评论 取消回复