【MATLAB图像融合】[11]小波变换在图像融合的简单应用

简述

       如果将图像理解为信号，那么图像就可以有时域和频域。小波变换的目的就是将图像从时域变换到频域，变换之后的图像具备某些鲜明的特点可以用于图像融合。这就是小波变换最简单的运用原理。

小波分解和小波重构

function wave=wtfusion(x1,x2,N,2name)
x1=double(x1);x2=double(x2);
[C1,S1]=wavedec2(x1,N,2name);
%wname即是小波基的名称。
[C2,S2]=wavedec2(x2,N,wname);
A1=appcoef2(C1,S1,wname,N);
%提取出小波分解的低频分量。
A2=appcoef2(C2,S2,wname,N);
A=0.5*A1+0.5*A2;
%融合低频分量。
a=reshape(A,1,S1(1,1)*S1(1,2));
%将A转换成行向量
C=a;
for i=N:-1:1
%循环从第N层到第1层
[H1,V1,D1]=detcoef2('all',C1,S1,i);
%提取出小波分解的各层细节分量
[H2,V2,D2]=detcoef2('all',C2,S2,i);
H=0.5*H1+0.5*H2;
%融合高频分量。
D=0.5*D1+0.5*D2;
V=0.5*V1+0.5*V2;
h=reshape(H,1,S1(N+2-i,1)*S1(N+2-i,2));%分别将融合后的细节分量转成行向量，并存入行向量C中
v=reshape(V,1,S1(N+2-i,1)*S1(N+2-i,2));
d=reshape(D,1,S1(N+2-i,1)*S1(N+2-i,2));
C=[C,h,v,d];
end
S=S1;
wave=waverec2(C,S,wname);
%重构原图像
end

运行结果：

结论
主函数调用部分省略，想要获得更好的融合效果需要自行设计高低频的融合规则，比较常规的：低频可以采用梯度阈值法，高频可以采用相似度法结合区域能量/采用块状的融合也可行。
这种04年被广泛研究的老方法，信息熵的提升会比较大，但是交叉熵，互信息的指标会比较低。原因还是在于一是源图像的利用度太低，没有挖掘像素之间，区块之间的关联，二是分解方法（小波分解）性能上落后于如今的新的尺度分解方法。
当然。对于小波的方法，我们还可以这样应用：

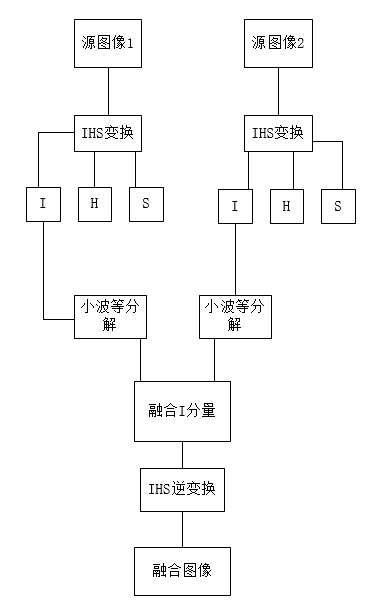
或者这样应用：

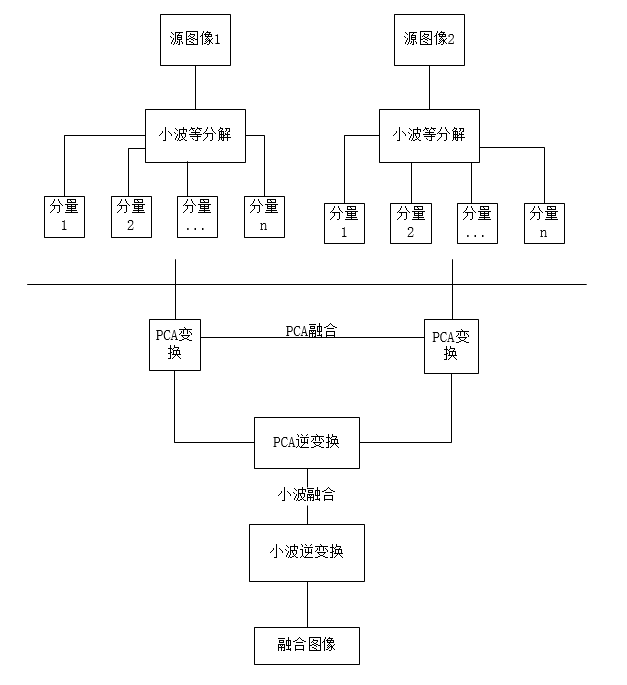
最后

以上就是雪白鞋垫为你收集整理的【MATLAB图像融合】[11]小波变换在图像融合的简单应用的全部内容，希望文章能够帮你解决【MATLAB图像融合】[11]小波变换在图像融合的简单应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。