1.LDPC译码的背景及内容
LDPC译码分为硬判决译码和软判决译码。
硬判决译码又称代数译码,主要代表是比特翻转(BF)译码算法,它的实现比较简单,但是译码性能很差。硬判决译码的基本假设是当校验方程不成立时,说明此时必定有比特位发生了错误,而所有可能发生错误的比特中不满足检验方程个数最多的比特发生错误的概率最大。在每次迭代时翻转发生错误概率最大的比特并用更新之后的码字重新进行译码。
软判决译码是一种基于概率论的译码算法,通常需要与迭代译码进行结合,才能体现成译码性能的优势,基本算法是置信传播(BP)译码算法,它的实现比代数译码方法的复杂度高很多,但译码性能非常好。
为了解决BP译码算法实现困难问题,在学术界牵起了优化算法的浪潮,对数域置信传播译码(LLR BP)算法、最小和(Min-Sum)译码算法、Normalized Min-Sum译码算法、Offset Min-Sum译码算法等相继涌现。
在迭代译码的过程中,信息调度方式分为两种:泛滥式调度和分层式调度。泛滥式调度的特点在于每一次译码迭代过程中,首先计算从变量节点到校验节点的所有软信息,然后计算从校验节点到变量节点的所有软信息。分层调度的特点是在计算每层软信息时,更新此次迭代中的相关的节点信息,用于下一层的软信息计算。
LDPC译码结构的设计方面主要分为三种:全并行译码结果、行并行译码结构、块并行译码结构。泛滥式的调度比较适合全并行结构,但是译码器的硬件复杂度始终是一个技术瓶颈。分层式的调度适合行并行和块并行结构,可以减少译码所需的迭代次数。
2.LDPC码设计
LDPC码是一种分组码,其校验矩阵只含有很少量非零元素(稀疏矩阵)。
码的设计是以设计一个校验矩阵开始的,然后才通过它确定一个生成矩阵进行后续编码。而LDPC的编码就是本文所要讨论的主体内容。对于LDPC码而言,校验矩阵的选取十分关键,不仅影响LDPC码的纠错性能力,也影响LDPC编译码的复杂度及硬件实现的复杂度。准循环LDPC码(Quasi-Cycle,QC-LDPC)是LDPC码中重要的一类,是指一个码字以右移或左移固定位数的符号位得到的仍是一个码字。QC-LDPC码的校验矩阵是由循环子矩阵的阵列组成,相对于其他类型的LDPC码,在编码和解码的硬件实现上具有许多优点。
置信传播(BP)译码算法,置信传播算法是基于Tanner图的迭代译码算法。在迭代过程中,可靠性消息,即“消息”通过Tanner图上的边在变量节点和校验节点中来回传递,经多次迭代后趋于稳定值,然后据此进行最佳判决,BP译码算法有着非常好的译码性能。
校验矩阵:
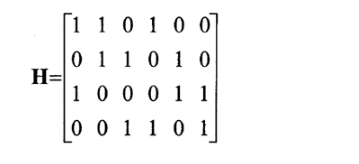
对应Tanner 图:
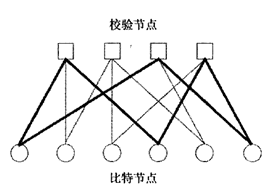
n个码字比特顶点(称为比特节点),分别与校验矩阵的各列相对应;
m个校验方程顶点(称为校验节点),分别与校验矩阵的各行对应。
循环以这群顶点中的一个同时作为起点和终点,且只经过每个顶点一次。循环的长度定义为它所包含的连线的数量,而图形的围长,也可叫做图形的尺寸,定义为图中最小的循环长度。上图围长为6。
2.1置信传播算法
置信传播算法(Belief Propagation)译码算法是消息传递(Message Passing)算法在LDPC译码中的运用。消息传递算法是一个算法类,最初运用于人工智能领域,人们将其运用到LDPC码的译码算法中,提出来LDPC码的置信传播算法。置信传播算法是基于Tanner图的迭代译码算法。在迭代过程中,可靠性消息,即“消息”通过Tanner图上的边在变量节点和校验节点中来回传递,经过多次迭代后区域稳定值,然后据此进行最佳判决。
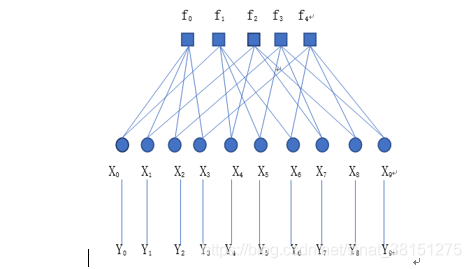
置信传播译码算法的基本流程如下:
在迭代前,译码器接收到信道传送过来的实值序列y = (y1,y2,…,yn),所有变量节点接收到对应的接收值yi。
第一次迭代:每个变量节点给所有与之相邻的校验节点传送一个可靠消息,这个可靠消息就是信道传送过来的值;每个校验节点接收到变量节点传送过来的可靠消息之后,进行处理,然后返回一个新的可靠消息信息给与之相邻的变量节点,这样就完成第一次迭代;此时可以进行判决,如果满足校验方程,则不需要再迭代,直接输出判决结果,否则进行第二次迭代。
第二次迭代:每个变量节点处理第一次迭代完成时校验节点传送过来的可靠消息,处理完成后新的消息发送给校验节点,同理,校验节点处理完后返回给变量节点,这样就完成了第二次迭代。完成后同样进行判决,如果满足校验方程则结束译码,否则如此反复多次迭代,每次都进行判决,直到达到设定的最大迭代次数,译码失败。在每次迭代过程中,无论是变量节点传送给校验节点的信息或者校验节点传送给变量节点的信息,都不应该包括前次迭代中接收方发送给发送方的信息,这样是为了保证发送的信息与接受节点已得到的信息相互对立。
译码结束:
如果或者达到最大译码迭代次数时,译码停止。
2.2对数域置信传播算法
置信传播算法中包含大量乘法运算,乘法运算结果稳定性比较差,波动性高,且复杂度高,运算时间较长,因而出现了对数域置信传播算法,将概率消息用对数似然比进行表示,概率域的乘法转换成对数域的加法。
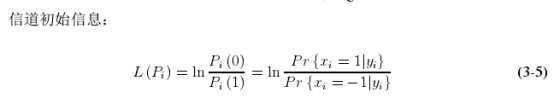

根据以上,LLR BP译码算法的迭代译码步骤如下:
(主要是根据3-9对数域、概率域之间的转换)


以上可知,LLR BP相较于BP译码算法在保证译码性能的同时也大大减少了运算的复杂度。
2.3最小和译码算法
最小和译码(MS,Min-Sum)算法是以LLR BP算法译码为基础,对校验节点信息更新的表达式进行的简化,其余步骤均与LLR BP译码算法一致。
Tanh函数:
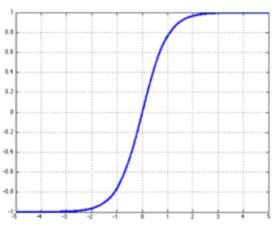
由上图,可以知道tanh的一些特点。tanh函数是奇函数,定义域内单调增加,值域在(-1,1)之间。


比较LLR BP译码算法和Min-Sum译码算法的校验节点信息更新过程,可以看到他们的主要区别在于LLR BP译码算法中的tanh(.)运算和加法运算在Min-Sum译码算法中被最小值和运算符号进行替换,MS译码简化了LLR BP译码算法,降低了译码算法的复杂度。
2.4改进的最小和译码算法
Min-Sum算法的简化方案不是精确计算而是近似方案,因而计算出的校验节点信息值和原始的实际值会存在误差,即过大估计问题。这将会导致译码过程的收敛速度减慢,译码性能也会有所损失。因此,研究人员提出了两种有效的方案:Normalized Min-Sum算法和Offset Min-Sum算法。
(1)Normalized Min-Sum算法
算法主要思想是在MS算法计算校验节点信息更新的步骤中对计算结果乘一个修正因子进行调整,缩小两者之间的差距。

(2) Offset Min-Sum算法
算法主要思想是在MS算法计算校验节点更新信息的步骤中对计算结果减一个修正因子进行误差补偿。

这两种改进方案复杂度差不多,但在译码性能方面远超MS译码算法,具有比较接近LLR BP译码算法的性能。
最后
以上就是开放小伙最近收集整理的关于LDPC译码原理1.LDPC译码的背景及内容2.LDPC码设计的全部内容,更多相关LDPC译码原理1.LDPC译码内容请搜索靠谱客的其他文章。








发表评论 取消回复