一、Simulink仿真基础

1、Simulink的启动

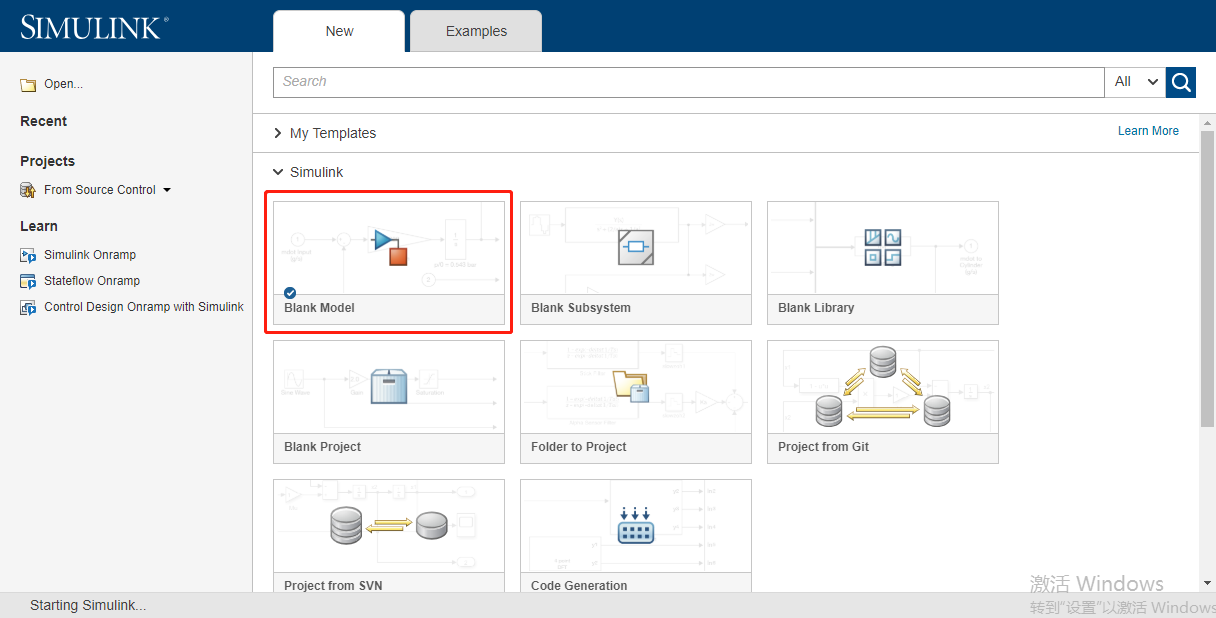
2、系统仿真模型的创建

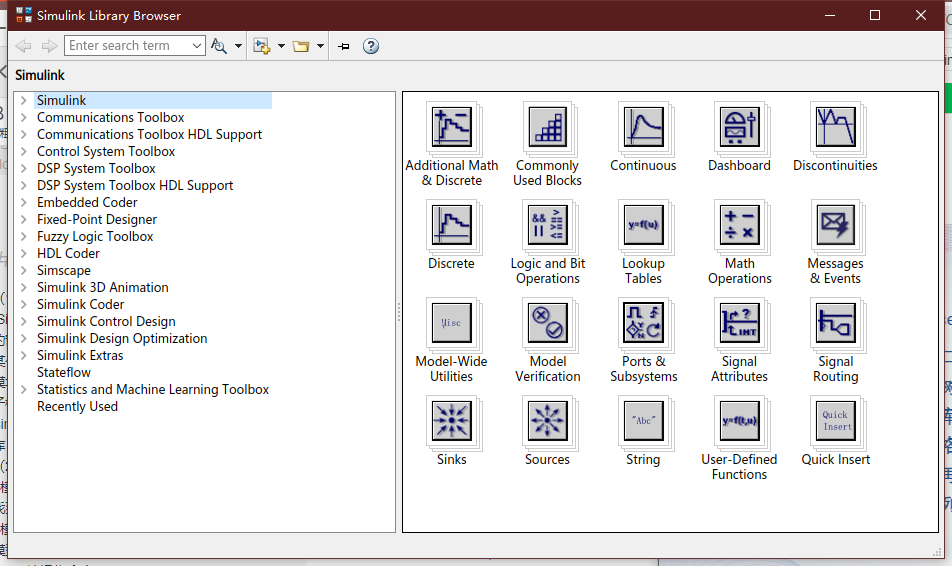
（1）Simulink Library Browser窗口
“Simulink模块库浏览器”窗口包含两个窗格，左侧的窗格以树状列表的形式列出所有模块库。单机某个模块库，即在右侧窗格中列出该模块库的子模块库；再双击其中的子模块库图标，即列出该子模块库的所有模块。
Simulink模块库大体分两类，一类是基本模块库，即Simulink模块库；另一类是专业模块库。

（2）Simulink模块的操作

• 模块的添加：首先在Simulink模块库浏览器窗口找到该模块，然后用鼠标拖拽。
• 模块的删除或幅值；选中模块按删除键。或者在模型编辑窗口选择Edit菜单项中的Cut、Copy、Paste等操作命令。
• 两个模块的连接：鼠标操作。
• 连线的分支：Ctrl+鼠标右键

（3）模块参数的设置

• 双击要设置的模块
• 选择要设置的模块，再选择Diagram——Block Parameters命令
• 右击要设置的模块，从快捷菜单中选择Block Parameters命令

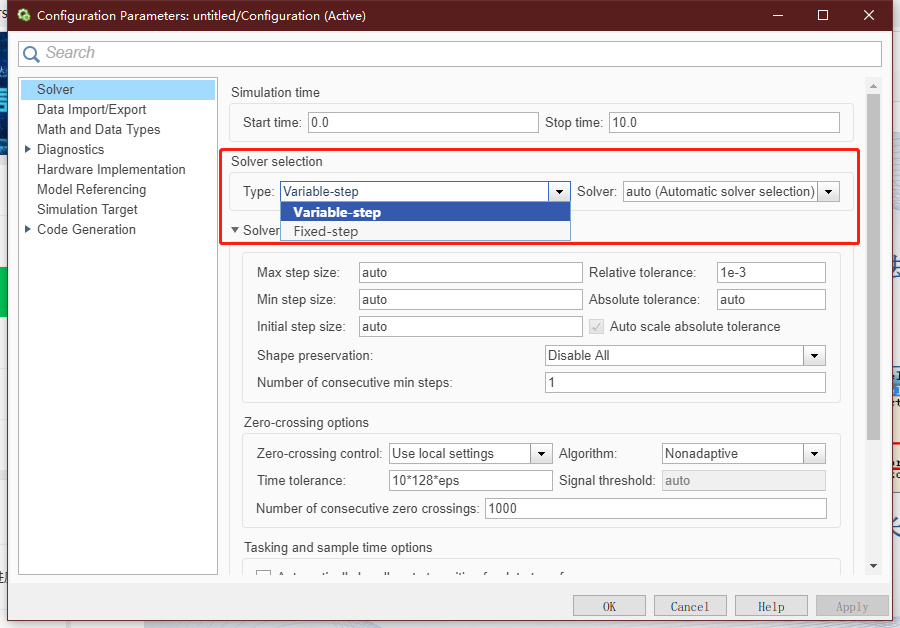
3、仿真参数的设置

• 选择Simulation——Model Configuration Parameters命令。
• 或者单击工具栏中的Model Configuration Parameters命令。

在仿真参数设置对话框中，仿真参数分为7类。仿真算法的选择首先要设定算法类别：固定步长或变步长算法，再选择具体算法。不同的模型选择不同的算法，比如刚性模型问题选择变步长算法。
设置完仿真参数之后，点击Run命令，便可以启动对模型的仿真。

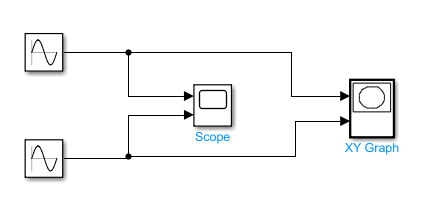
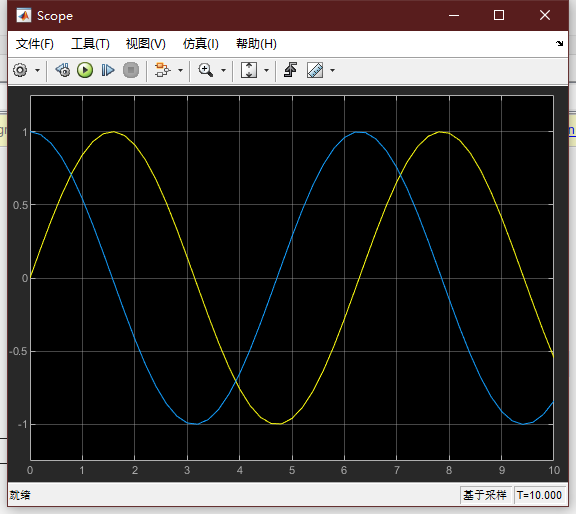
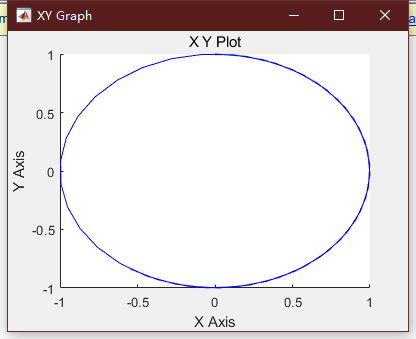
例子：利用Simulink仿真，分别显示曲线y=sint和y=cost，同时显示sint对cost的变化曲线。
解：正弦信号，由信号源模块库（Source）中正弦信号模块提供。余弦信号还是由正弦信号模块提供，只是相角设为pi/2。

二、子系统的创建与封装

1、子系统的创建

• 通过Subsystem模块建立子系统
• 将已有的模块转换为子系统

两者的区别是：前者先建立子系统，再为其添加功能模块；后者先选择模块，再建立系统。

例子：创建y=kx+b的子系统
（1）通过Subsystem模块建立子系统

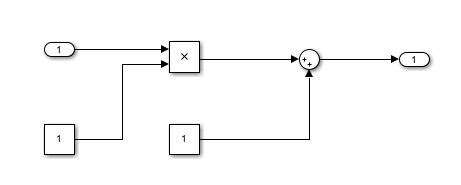
• 双击子系统模块打开子系统编辑窗口，窗口中已经自动添加了相互连接的一个输入模块和输出模块，表示子系统的输入端口和输出端口。将要组合的模块插入到输入模块和输出模块中间，这里需要要k和b两个常熟模块，一个乘法模块和一个加法模块，将这些模块重新连接起来，一个子系统就建好了。
  
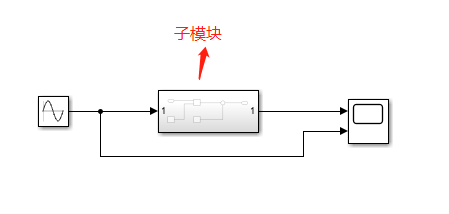
• 启动仿真后查看示波器的曲线，其中蓝色曲线是正弦曲线，黄色曲线是经过y=kx+b变换之后的曲线，这里在MATLAB命令行窗口事先给k赋给3，b赋给2，即黄色曲线代表y=3sint+2。
  
  

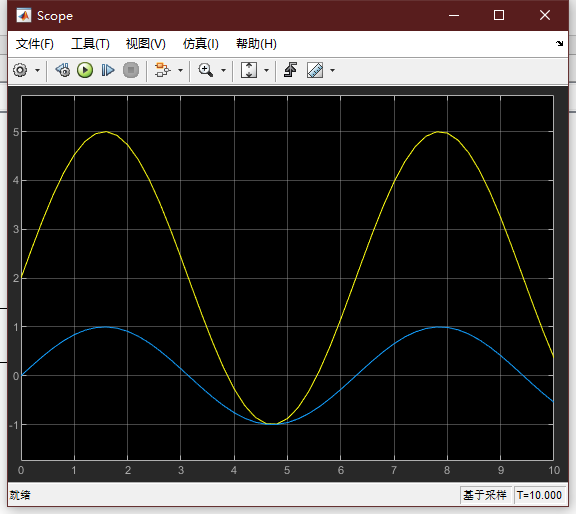
（2）通过已有的模块建立子系统

• 选择建立的系统模型中的所有模块，在模型编辑窗口选择Diagram菜单项中的相关命令（Diagram→Subsystem&Model Reference→Create Subsystem from Selection命令），或者按Ctrl+G组合键建立子系统，所选模块将一个子系统模块取代，如果想要查看子系统的内部结构可以双击子系统模块。

2、子系统的封装

（1）
先选中所要封装的子系统，再在模型编辑窗口选择COMPONENT菜单项中的Create Mask命令，或按Ctrl+M组合键，这时将出现封装编辑器（Mask Editor）对话框。

第一个选项卡用于设置被封装模块的图标；第二个选项卡用来设置子系统参数设置对话框；第三个选项卡用于设置初始化命令；第四个选项卡用于定义封装模块的类型、描述和帮助文本。

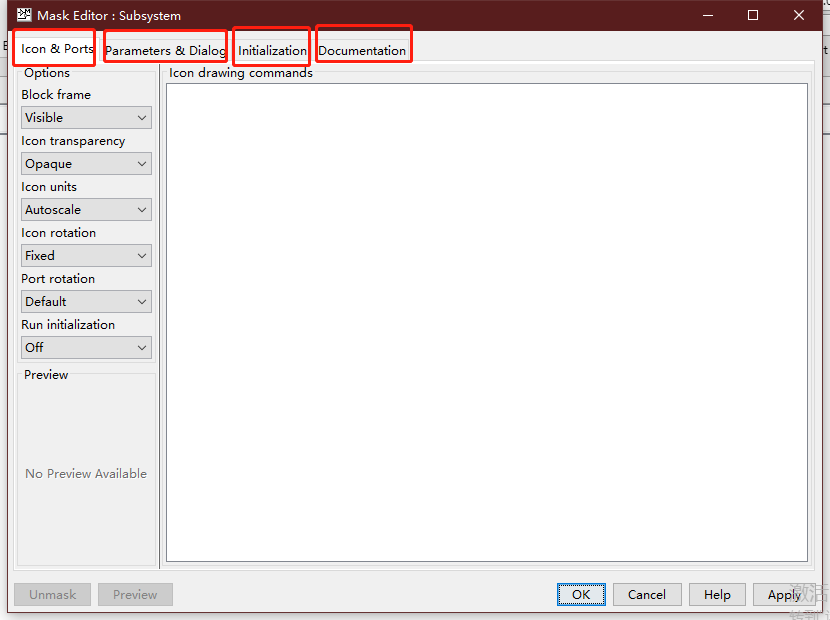
第二个选项卡由3部分组成，左侧为控件工具箱（Controls），中间区域显示对话框中的控件，右侧区域用于显示和修改控件的属性。

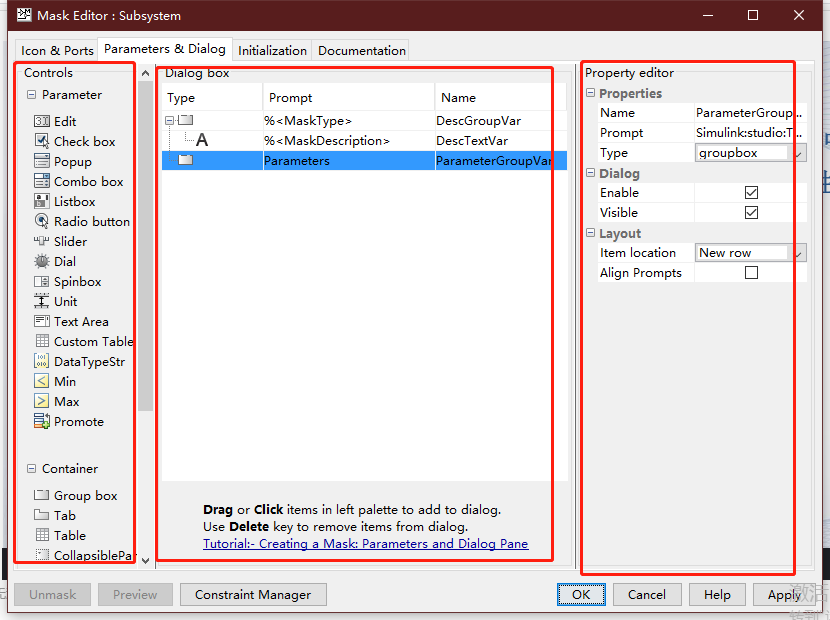
（2）以y=kx+b子系统为例，说明子系统参数设置对话框的设置方法
在第二个选项卡的左侧控件工具箱中，连续2次单机Edit按钮，为子系统的2个变量准备输入位置。在中间区域分别输入该控件的提示信息和控件名，最后单击ok确认设置。

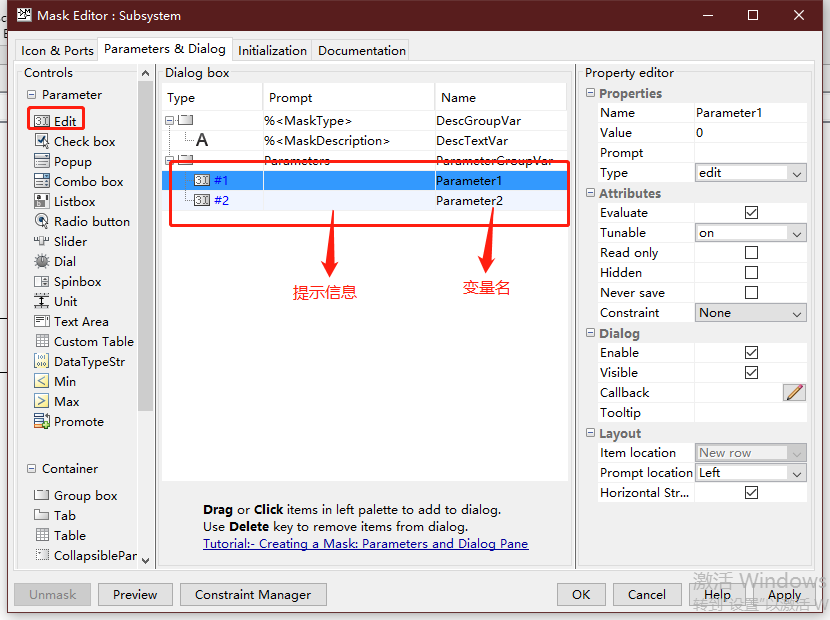
子系统参数设置对话框设置完成后，双击子系统图标将出现其参数对话框。例如，双击仿真模型中的y=kx+b子系统图标，则弹出如果所示的参数对话框，允许用户输入参数k和b

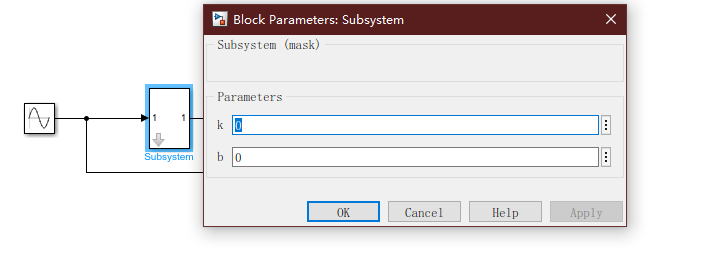
3、子系统的条件执行

s受控制信号的子系统称为条件执行子系统。在条件执行子系统中，输出信号取决于输入信号和控制信号。

条件执行子系统：

• 使能子系统
• 触发子系统
• 使能加触发子系统

（1）使能子系统
使能子系统表示控制信号由负变正时子系统开始执行，直到控制信号再次变为负时结束。控制信号可以是标量也可以是向量。如果是标量，则当标量的值大于0时子系统开始执行。如果是向量，在向量中任何一个元素大于0，子系统将执行。
使能子系统外观上有一个“使能”控制信号输入端口。“使能”是指当且仅当“使能”输入信号为正时，该模块才接收输入端的信号。可直接选择使能子系统模块来建立使能子系统，双击使能子系统模块，打开其内部结构窗口。也可以展开已有子系统，添加端口与子系统（Ports&Subsystems）模块库中的使能模块（Enable），将该子系统转换为使能子系统。

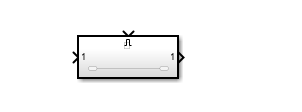
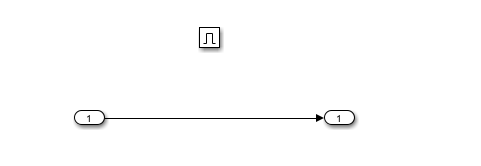
例1：利用使能子系统构成一个正弦半波整流器

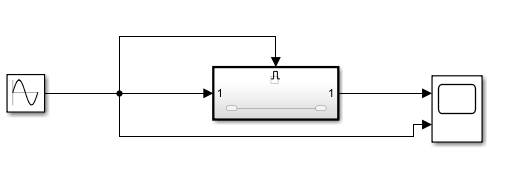
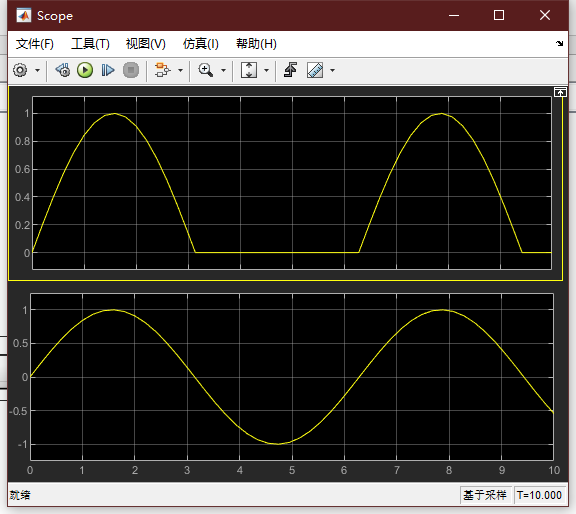
（2）触发子系统
触发子系统是指当触发事件发生时开始执行子系统。
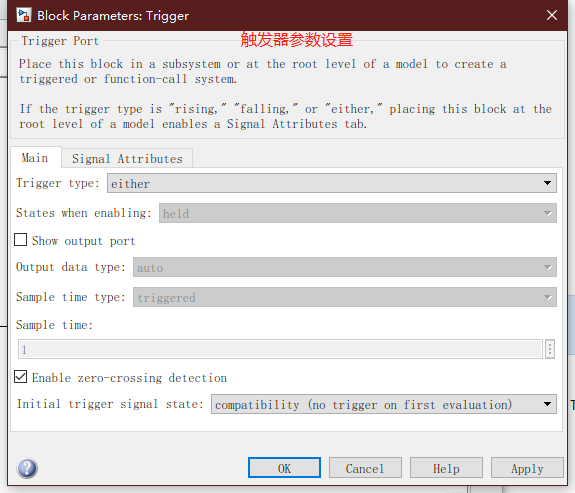
与使能子系统类似，触发子系统的建立可以直接选择Triggered Subsystem模块，或者展开已有子系统，添加Ports&Subsystem模块中的Trigger模块，将该子系统转换为触发子系统。

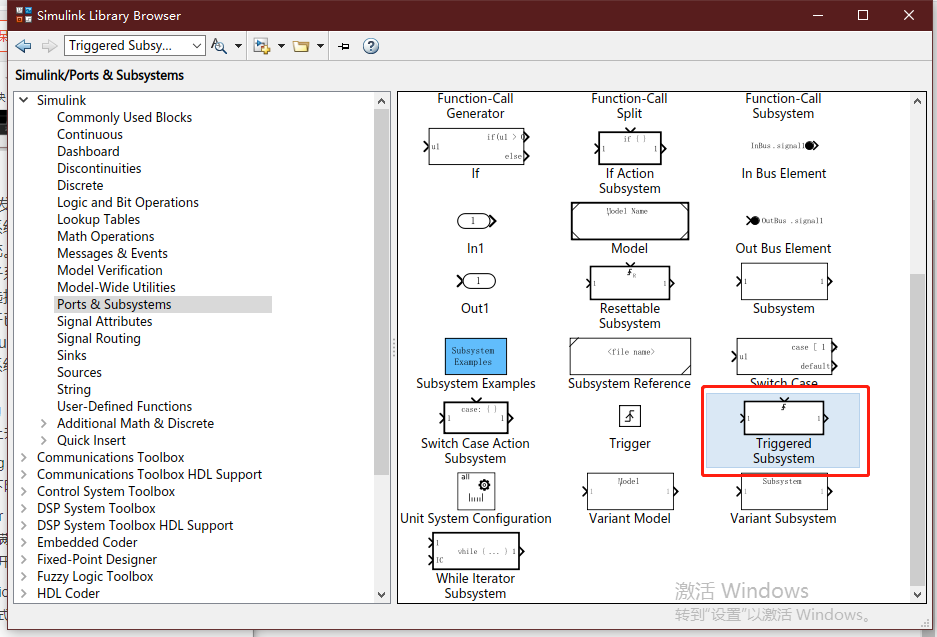
• rising（上调沿触发）：控制信号从负值或0上升到正值时子系统开始执行。
• falling（下跳沿触发）：控制信号从正值或0下降到负值时子系统开始执行。
• either（上跳沿或下跳沿触发）：当控制信号满足上跳沿或下跳沿触发条件时，子系统开始执行。
• function-call（函数调用触发）：这种触发方式必须与S函数配合使用。
  

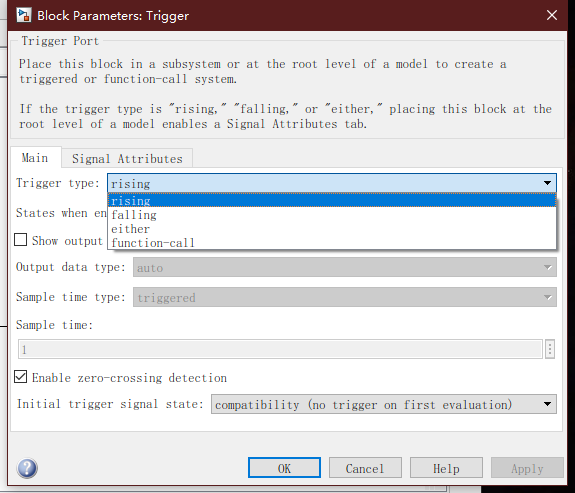
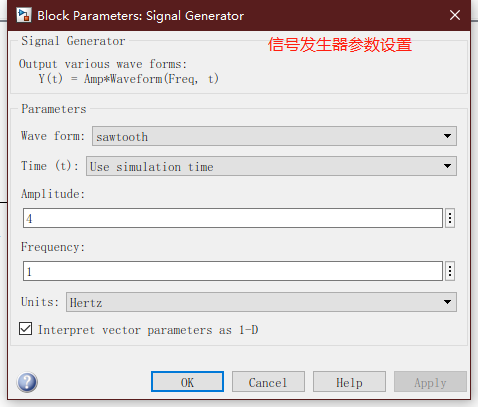
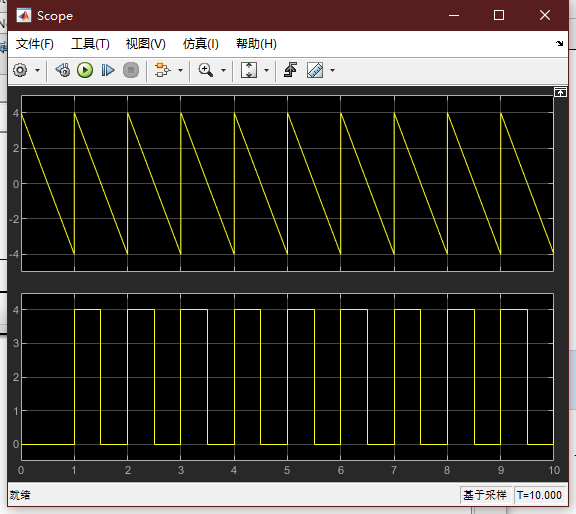
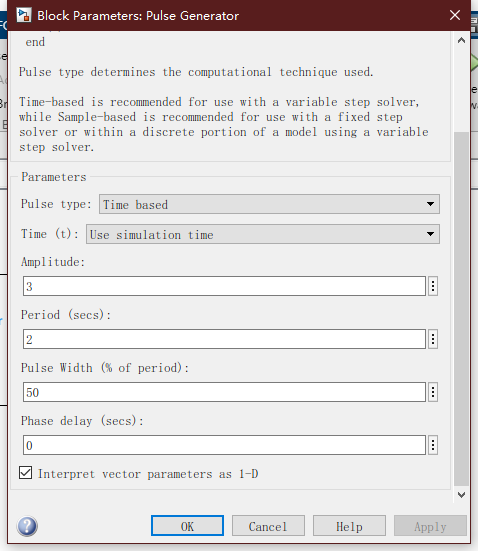
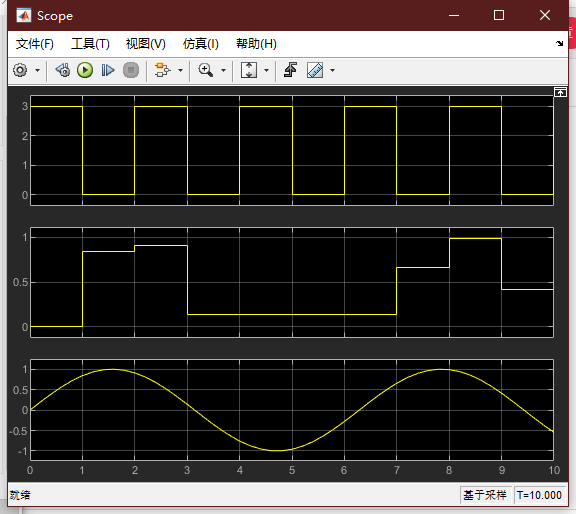
例2：利用触发子系统将一锯齿波转换成方波。

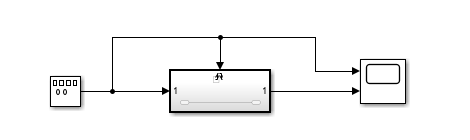
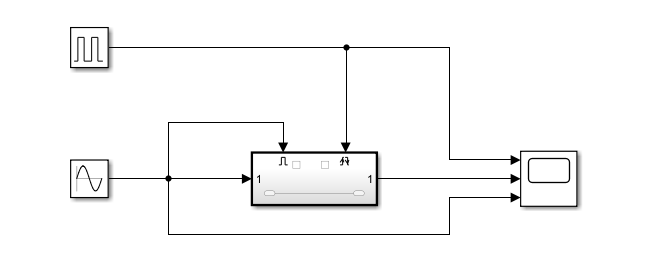
（3）使能加触发子系统
所谓使能加触发子系统就是当使能控制信号和触发控制信号共同作用时执行子系统。

三、S函数的设计与应用

1、S函数

• S函数是系统函数（System Function）的简称，是指采用一种程序设计语言描述的一个功能模块。
• 用户可以采用MATLAB 语言，也可以采用C、C++或FORTRAN等语言来编写S函数。
• S函数有自己特定的语法构成规则，可以用来描述并实现连续系统、离散系统以及复合系统。
• S函数能够接收来自Simulink求解算法的相关信息，并对求解算法发出的命令做出适当的响应，这种交互作用类似于Simulink系统模块与求解算法的相互作用。

2、用MATLAB语言编写S函数

edit sfuntmpl.m

模板文件sfuntmpl.m包括：1个主函数，6个子函数。
（1）主函数
引导句为：function[sys,x0,str,ts]=fname(t,x,u,flag)

• fname是S函数的函数名。
• 输入形参t,x,u,flag分别为其仿真时间、状态向量、输入向量和子函数调用标志。
• 输出形参sys代表一种返回参数；x0是初始状态值；对于M文件S函数，str将被置为一个空阵；ts是一个两列矩阵。

（2）子函数
S函数有6个子函数，这些子函数的前缀为mdl，由flag的值来控制在仿真的各阶段调用S函数的哪一个子函数。

• flag取0：调用初始化子函数mdlInitializeSizes。
• flag取1：调用子函数mdlDerivatives实现连续状态的更新。
• flag取2：调用子函数mdlUpdate实现离散状态的更新。
• flag取3：调用输出子函数mdlOutputs。

3、S函数的应用

采用S函数实现y=kx+b
（1）定义S函数
①主函数

function [sys,x0,str,ts] = timekb(t,x,u,flag,k,b)
switch flag
  case 0
    [sys,x0,str,ts]=mdlInitializeSizes;%初始化
  case 3
    sys=mdlOutputs(t,x,u,k,b);%计算输出量
  case {1,2,4,9}
    sys=[];
  otherwise
   error(num2str(flag))%出错处理

end

②初始化子函数

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 0;%无连续状态
sizes.NumDiscStates  = 0;%无离散状态
sizes.NumOutputs     = 1;%有一个输出量
sizes.NumInputs      = 1;%有一个输入信号
sizes.DirFeedthrough = 1;%输出量中含有输入量
sizes.NumSampleTimes = 1;%单个采样周期
sys = simsizes(sizes);%给其他返回参数赋值
x0  = [];%设置初始状态为零状态
str = [];%将str变量设置为空字符串
ts  = [-1 0];%假定继承输入信号的采样周期

③ 输出子函数

function sys=mdlOutputs(t,x,u,k,b)
sys =k*u+b;

（2）在Simulink模型中使用S函数
向模型编辑窗口中添加S函数模块、Sine Wave模块和Scope模块。

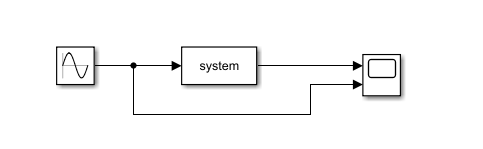
双击system模块，编辑参数
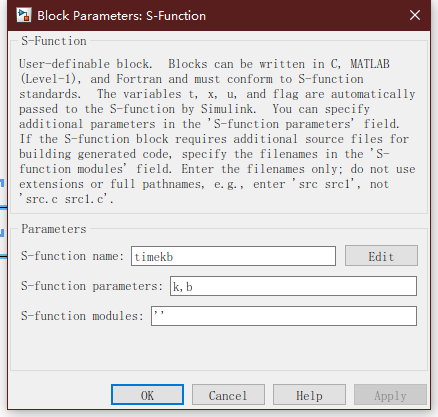在模型编辑窗口选择S函数模块，打开封装编辑器

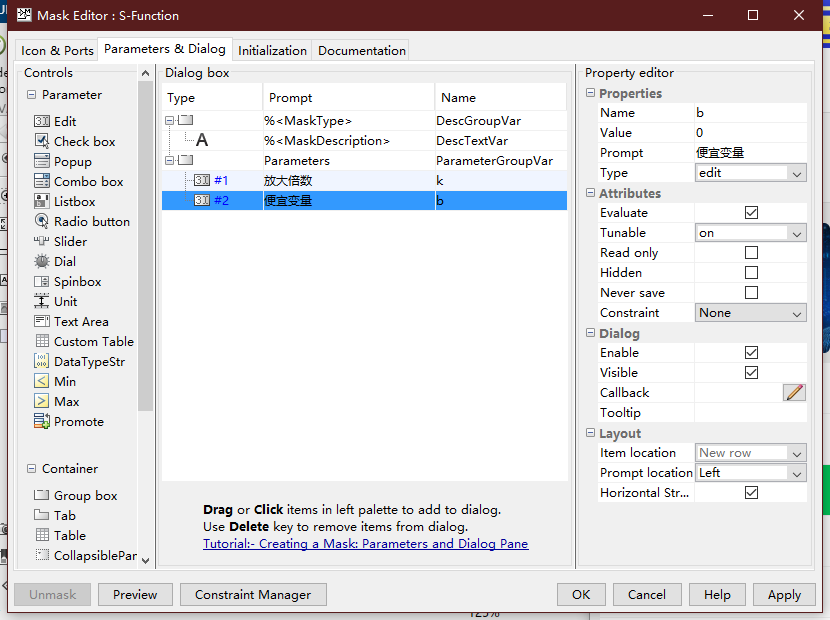
S函数封装后，双击打开参数对话框

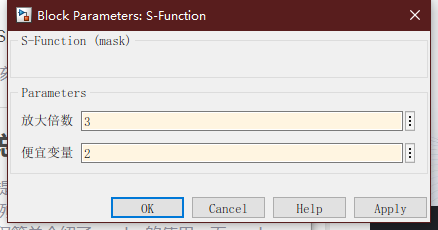
Run运行结果

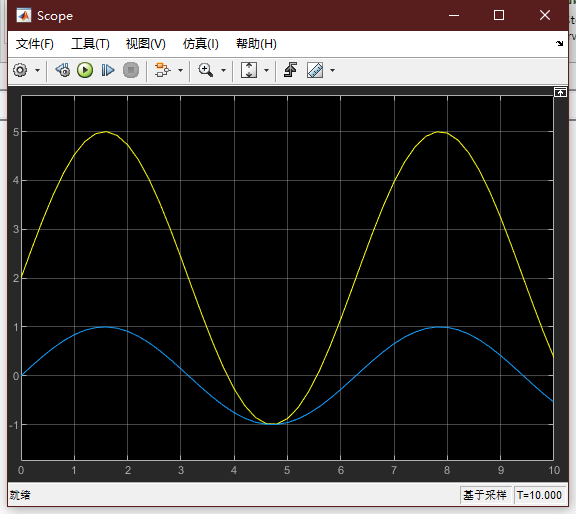
四、Simulink仿真应用举例

• 建立蹦极跳系统的Simulink仿真模型
• 分析蹦极跳系统的安全性，包括：
  – 当弹力绳弹性系数一定时，求蹦极者的安全体重。
  – 当蹦极者体重一定时，求弹力绳的最小弹性系数。

1、蹦极跳系统的Simulink仿真模型

（1）系统分析

（2）仿真模型
$(mg+b(y)-a_1{y}^{\prime }-a_2{y}^{\prime }|y^{\prime }|)\ast (\frac{1}{m})=y^{\prime \prime }$

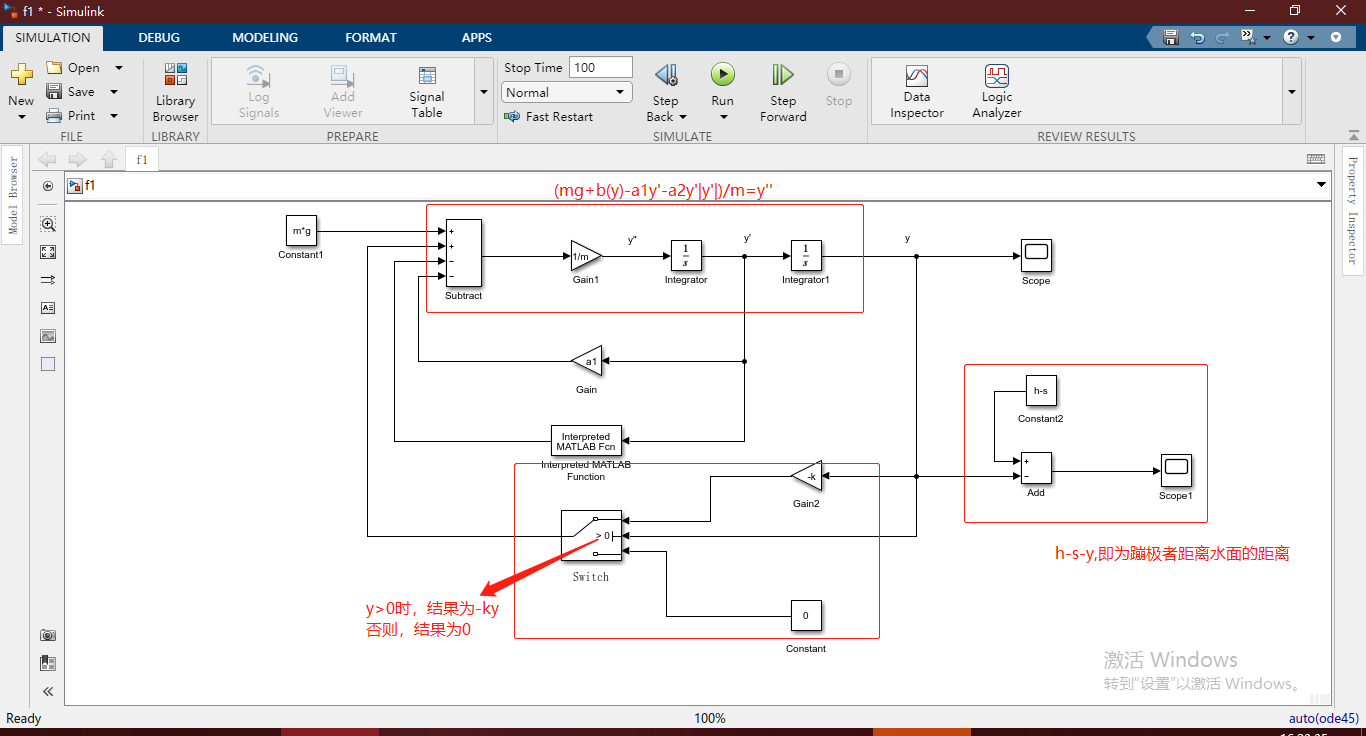
（3）仿真结果分析
分别设置两个积分模块的初始值

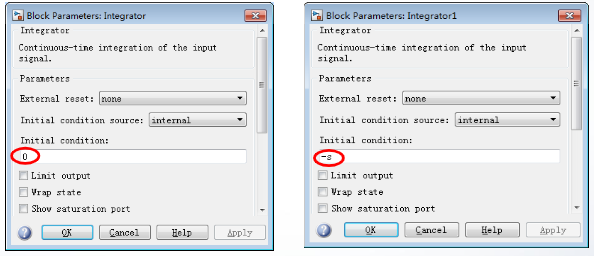
在MATLAB命令行窗口输入参数值

m=75;g=9.8;k=20;a1=1;a2=1;h=100;s=40;

时间设置为100，开始运行


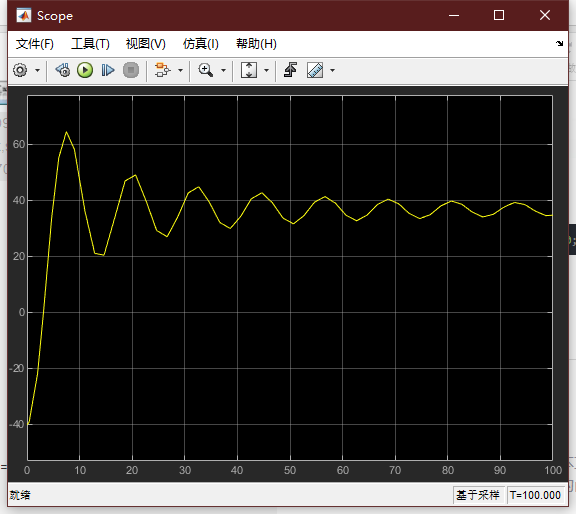
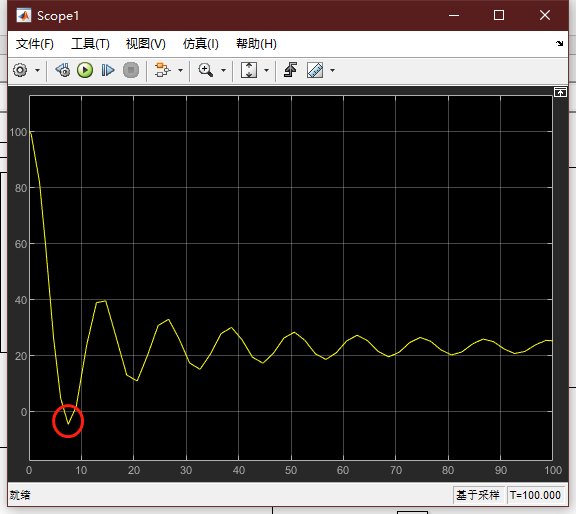
可见，此时蹦极者距离水面的距离存在小于0，说明这种状态下不安全。将m改为65，其他不变，查看此时曲线：

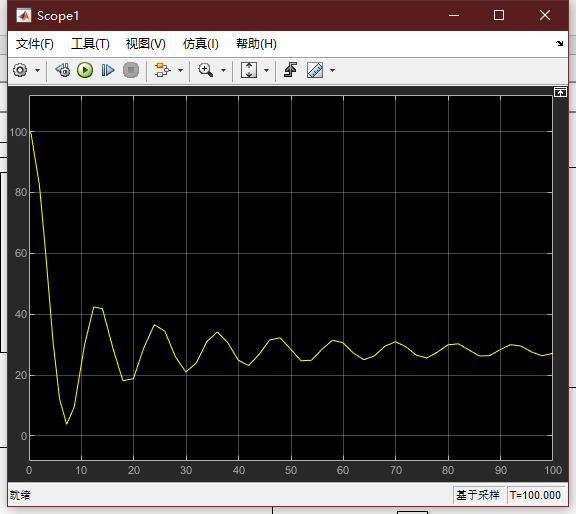
此时是安全的。所以，在其它系统参数确定的情况下，对蹦极者的体重是有要求的。

2、分析蹦极跳系统的安全性

– 当弹力绳弹性系数一定时，求蹦极者的安全体重。
– 当蹦极者体重一定时，求弹力绳的最小弹性系数。
（1）假设人与水面的最小距离是1.5m，系统其他参数不变，求蹦极者的安全体重。
在MATLAB 输入

for m=100:-0.5:20
    set_param('f1','ReturnWorkspaceOutputs','off');
    [t,x,y_w]=sim('f1',0:0.01:100);%f1是Simulink模型的文件名，t是仿真时间向量，x是状态矩阵，y_w是对应Out模块的输出矩阵
    if min(y_w)>1.5
        break;
    end
end
disp(['最大安全体重是',num2str(m)])
dis=min(y_w);
disp(['最小的安全距离是',num2str(dis)])
plot(t,y_w)
grid on

结果是
最大安全体重是67.5
最小的安全距离是1.6803

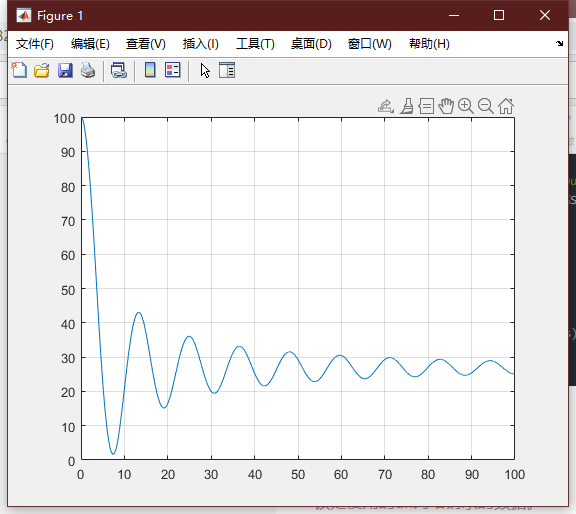
（2）假设人与水面的最小距离是1.5m，求蹦极者的体重是65kg，系统其他参数不变，求最小弹性系数。
代码

m=65; 
for k=10:0.1:50
    set_param('f1','ReturnWorkspaceOutputs','off');
    [t,x,y_w]=sim('f1',0:0.01:100);
    if min(y_w)>1.5
        break;
    end 
end
disp(['最小弹性系数k是',num2str(k)])
dis=min(y_w);
disp(['最小的安全距离是',num2str(dis)])
plot(t,y_w)
grid on

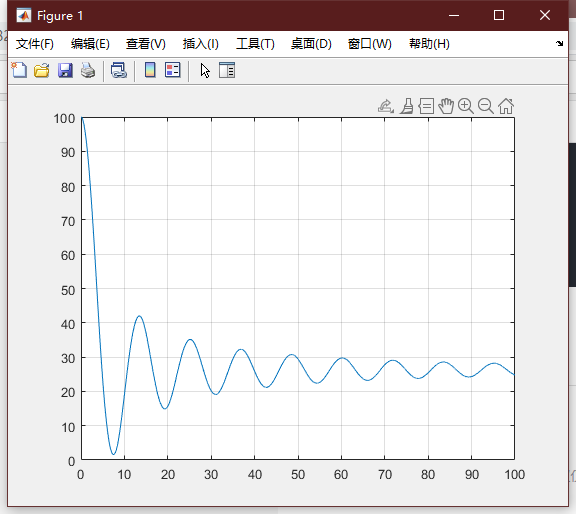
运行结果
最小弹性系数k是18.9
最小的安全距离是1.5521

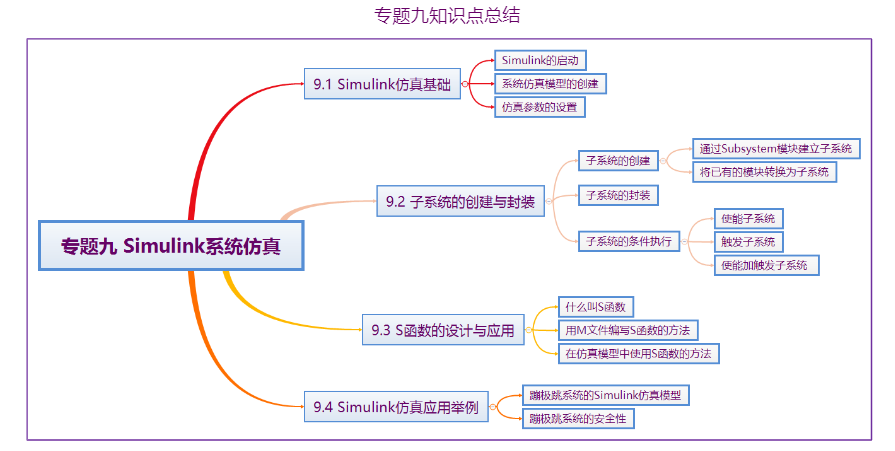
总结

最后

以上就是野性月光为你收集整理的专题九Simulink仿真基础一、Simulink仿真基础二、子系统的创建与封装三、S函数的设计与应用四、Simulink仿真应用举例总结的全部内容，希望文章能够帮你解决专题九Simulink仿真基础一、Simulink仿真基础二、子系统的创建与封装三、S函数的设计与应用四、Simulink仿真应用举例总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。