控制教程 —— 介绍篇：8.基于Simulink为火车系统建模

在Simulink中，对物理系统的数学模型进行建模和仿真是非常简单的。模型在Simulink中是以图形框图的方式表示，用户可以在提供的模型库中找到各种模块。使用Simulink进行动态系统分析的主要优点之一，它使我们能够快速分析复杂系统的响应，而这些系统可能很难分析。Simulink能够从数学上近似解决我们无法或难以手动解决的数学模型。
通常，可以从物理定律中得出关于给定系统的数学方程，它是Simulink建模的基础。本次教程中，我们将演示如何导出数学模型，然后在Simulink中实现该模型。

火车系统

在这个示例中，我们将考虑由引擎和车厢组成的玩具火车。假设火车仅在一个维度上(沿着轨道)行驶，我们希望对火车进行控制，使其平稳的启动和停止，并在稳定状态下具有最小的误差来跟踪给定速度。
火车头和车厢的质量分别用 $M_1$ 和 $M_2$ 表示。此外，火车头和车厢通过具有刚度 $k$ 的联轴器连接。换句话说，将联轴器可以等效成弹簧常数为 $k$ 的弹簧来建模。 $F$ 表示火车头的牵引力，而 $\mu$ 表示滚动摩擦系统。

受力分析和牛顿第二定律

推导控制物理系统的数学方程式的第一步就是绘制系统的受力图，以下是针对我们的火车系统的分析：

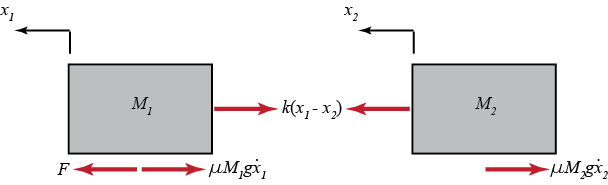
根据牛顿第二定律，我们知道作用在物体上的合力等于物理质量及其加速度的乘积。在这种情况下，水平方向上作用在火车头 $M_1$ 上的力由牵引力，弹力，摩擦力组成，作用在车厢 $M_2$ 上的力由弹力和摩擦力组成。在垂直方向上，重力和地面施加的法向力 (N=mg)平衡。因此，在最值方向上没有加速度。
我们将弹簧建模为弹力与形变成线性比例的关系。即 $k(x_1-x_2)$，其中 $x_1$ 和 $x_2$ 分别是火车头和车厢的位移。这里假设当 $x_1$ 和 $x_2$ 等于零时，弹簧没有形变。将摩擦力建模成与速度和法向力(等于重力)的乘积成线性比例的关系。
根据上述受力分析，在水平方向上应用牛顿第二定律可以得出以下列车系统控制方程：
$$\Sigma F_1=F-k(x_1-x_2)-\mu M_{1}g{\dot{x}}_1=M_1{\ddot{x}}_1$$$$\Sigma F_2=k(x_1-x_2)-\mu M_{2}g{\dot{x}}_2=M_2{\ddot{x}}_2$$

构建Simulink模型

我们将构建两个模型(每个质量一个)，通过表达式 $\Sigma F=ma$ 或 $a=(\Sigma F)/m$。首先，打开Simulink并新建一个模型窗口，然后将两个求和模块(Math Operations库)拖到窗口中，并将它们放置在合适的位置，如下所示：

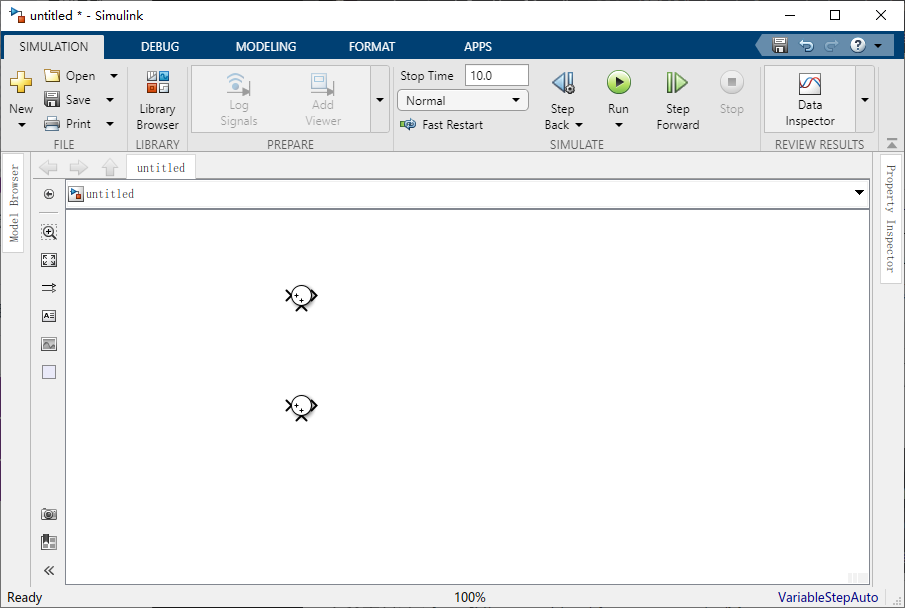
这些 sum模块中每个模块的输出表示作用在每个质量上的力之和。将每个输出信号乘以 $1/M$ 将得到每个质量块相应的加速度，现在，将两个 “Gain” 模块(Math Operations库)拖到窗口中，并在其中一个 “Sum” 模块的输出处添加标签 “Sum_F1” 和 “Sum_F2”，模型看起来会更加清晰，通过双击两条信号线并输入所需要的标签来完成这个操作。

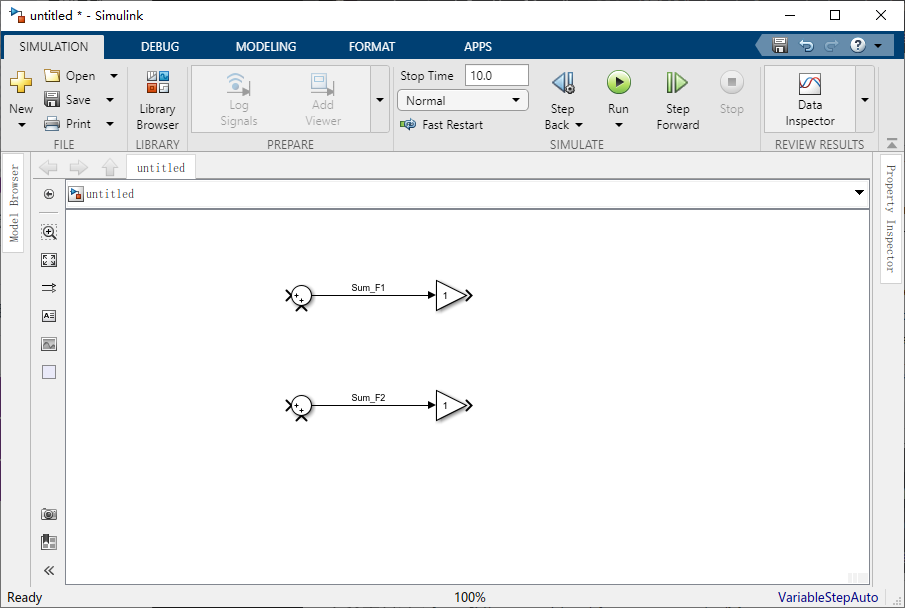
将这些增益模块默认的 K 更改为对应的质量块 $1/M$ ，我们在MATLAB工作区中定义变量 M1 和 M2。因此我们只需要在每个增益模块中输入相应的变量名称即可。双击上方的增益模块，然后再 “Gain” 字段中输入 “1/M1” 和 “1/M2”。
你会注意到修改后，“Gain” 有一层红色，这是没有定义 M1 和 M2。后续赋值后这个就会消失。

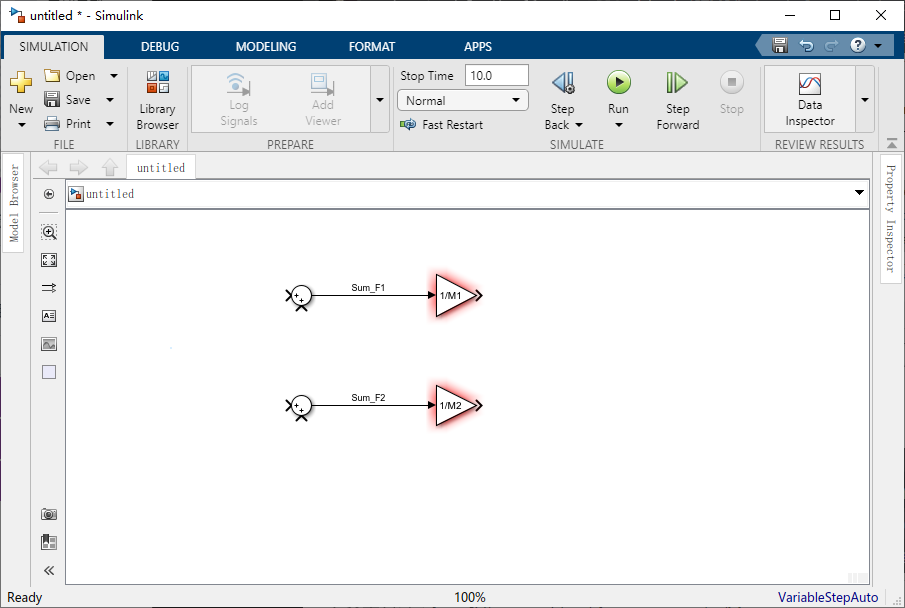
这个“Gain”模块输出的是每个物体(火车头和车厢)的加速度，我们上面推导的控制方程式取决于物体的速度和位移。由于可以通过积分加速度来获得速度，而我们再积分速度来获得位置，因此我们可以使用积分器模块来生成这些信号。从 Continuous库中将拖动四个Integrator模块到窗口中。

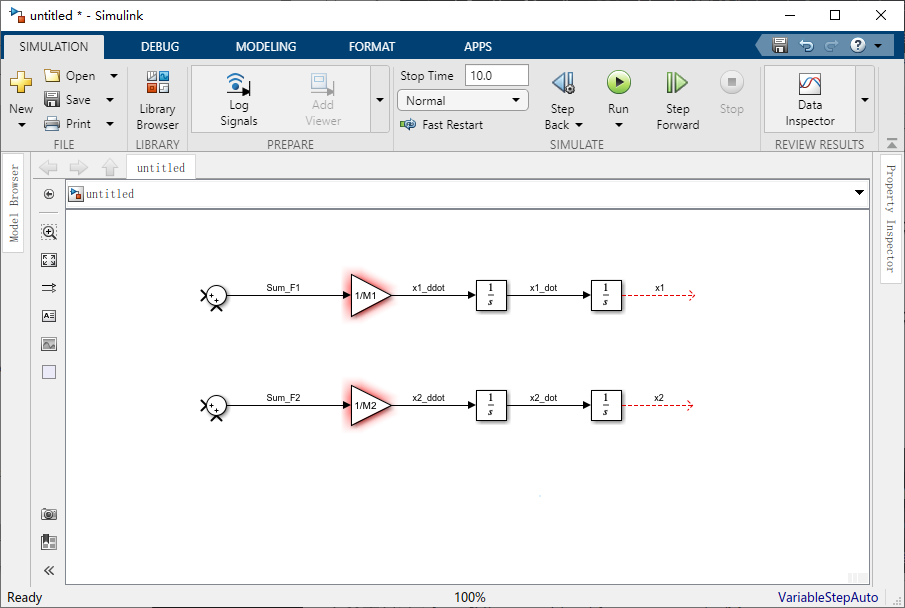
现在，将两个 Scope 从Sinks库中拖动到窗口中，并连接到这些积分器的输出，将它们分别标记为 “x1” 和 “x2”。

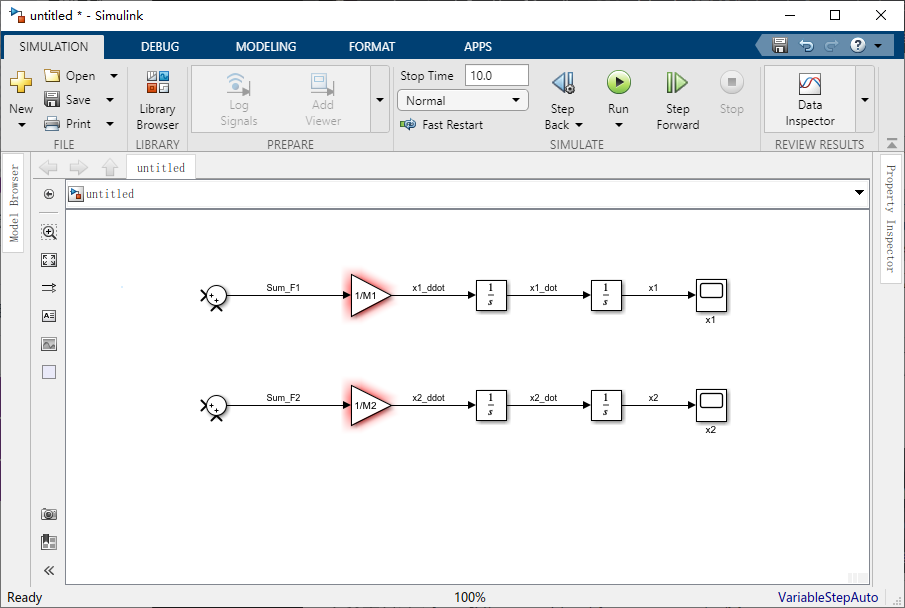
现在我们准备添加每个物体上的作用力。首先，我们需要调整每个 “Sum” 模块上的输入来表示作用力的个数。由于总共有三个作用在火车头上的力，双击相应的 “Sum” 模块并将 “List of signs” 字段更改为 “|+++”。符号 “|” 用作隔离。只有两个力作用在车厢上，因此我们不用考虑 “M2” 的 “Sum” 模块。

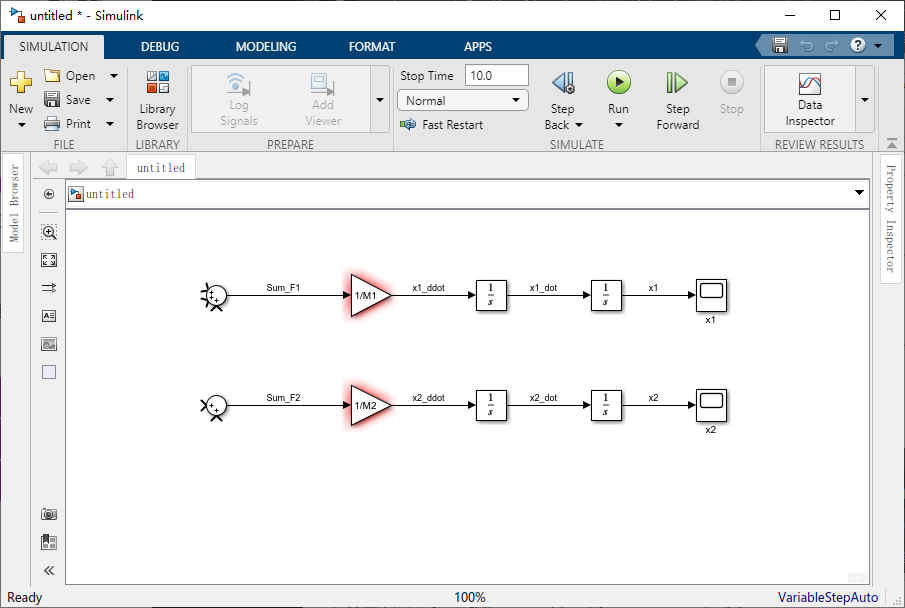
作用在火车头上的第一个力就是牵引力 $F$ 。 从 Sources库中拖动一个 Signal Generator模块到窗口中，并将其连接到相应的 Sum模块的最上面输入，该信号标记为 “F”。

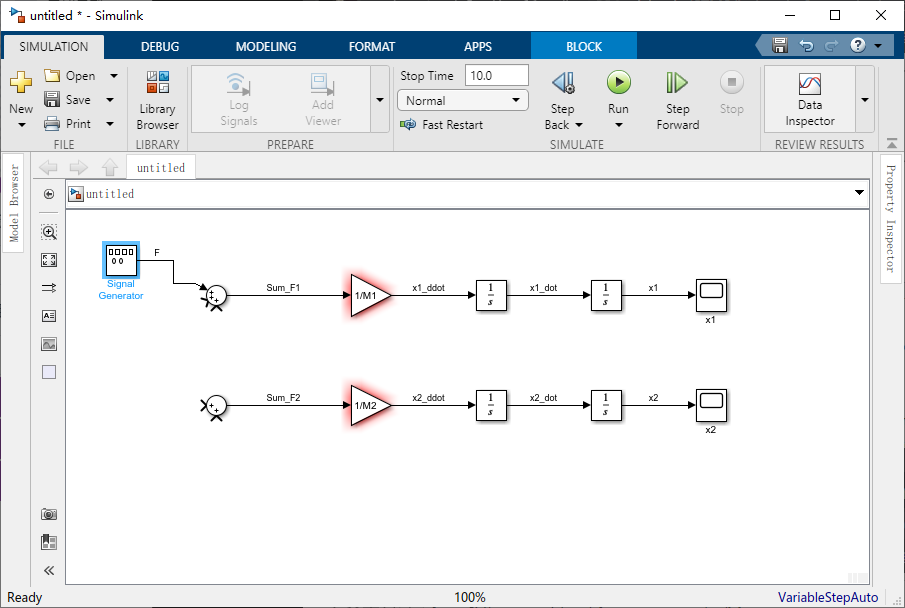
作用在火车头上的下一个力是摩擦力，回想一下，摩擦力的建模如下：
$$F_{rr,1}=\mu g{M}_1{\dot{x}}_1$$
为了产生这个力，我们可以提取速度信号并乘以适当的增益。将一个增益模块拖到窗口中，并拉出 “x1_dot” 信号，并将其连接到该新的增益模块的输入，将增益模块的输出连接到 “Sum” 的第二个输入。双击新的 “Gain” 输入 mu*g*M1。由于摩擦力是负，所以将 “Sum”的符号改成 “|±+”。并将新的 “Gain” 输出标记成 “Frr1” 。

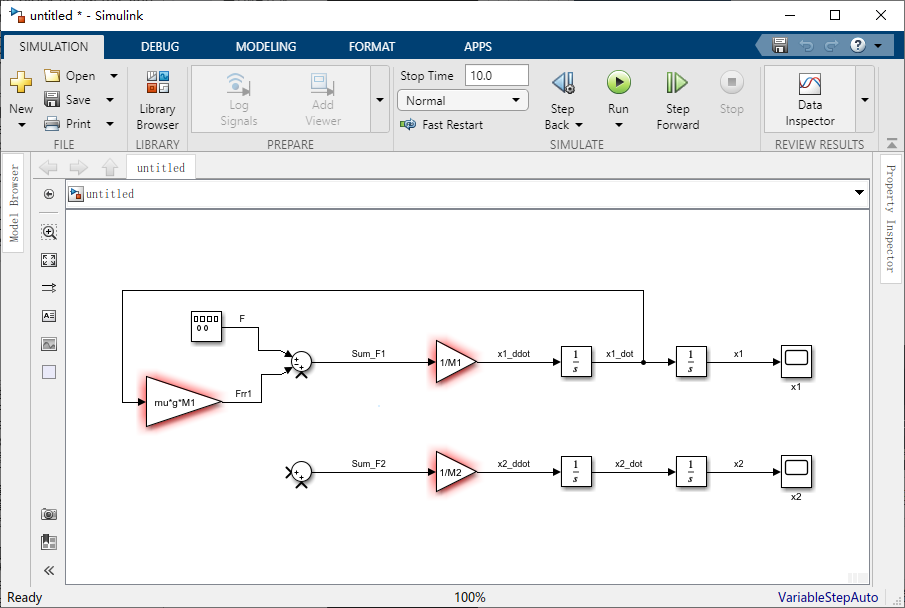
作用在火车头上的最后一个力是弹力，回想一下，弹力的建模为
$$F_s=k(x_1-x_2)$$
因此，我们需要生成信号 $x_1-x_2$ ，然后可以将其乘以增益 $k$ 来创建弹力。将减法模块(或求和模块或加法模块)拖到窗口中，为了更改该模块的方向，可以右击该模块，然后从出现的菜单Rotate & Flip > Flip block或者选中该模块，使用快捷键Ctrl-I。现在，将 “x2” 的信号连接到减法模块的负输入，同样，将 “x1” 的信号连接到减法模块的正输入。

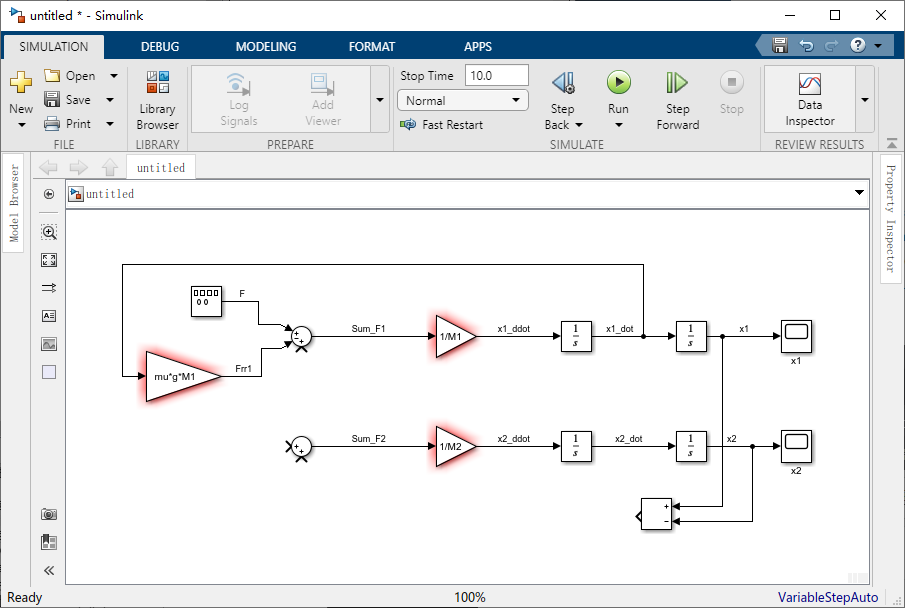
现在，我们将这个差值乘以弹簧常数以产生弹力。将一个增益模块拖到窗口中，将增益模块的值改为 “k” ，并将减法模块的输出连到增益模块的输入。然后将增益模块的输出连接到火车头的求和模块的第三个输入，并标记信号 “Fs” ，由于弹簧力沿负方向作用在火车头上，因此有必要将 “Sum” 模块的符号改成 “|±-” 。

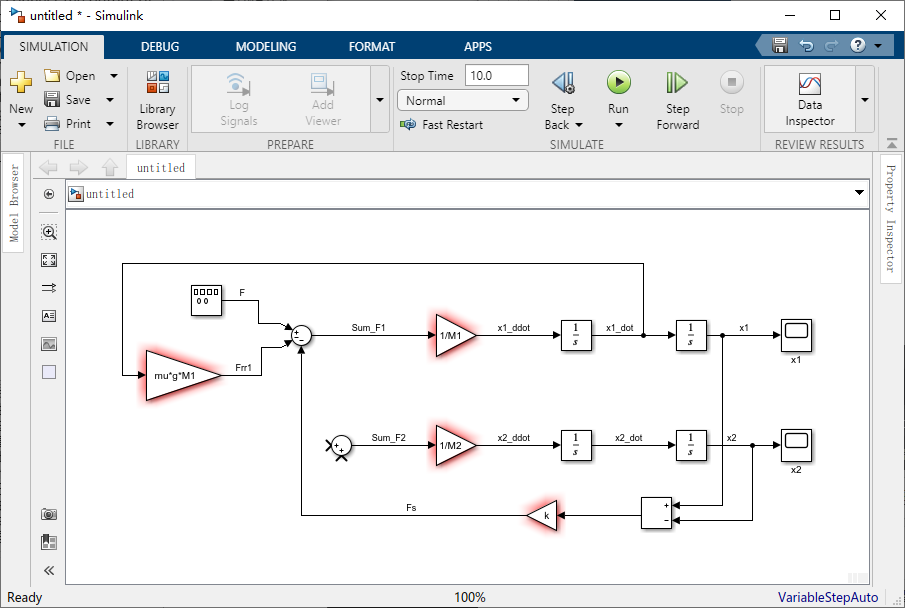
现在，我们可以对车厢施加作用里，对于第一个力，我们将使用刚产生的弹簧力。只是沿正方向施加到车厢上，只需将弹力 “Fs” 连接到车厢的 “Sum” 模块的第一个输入上。

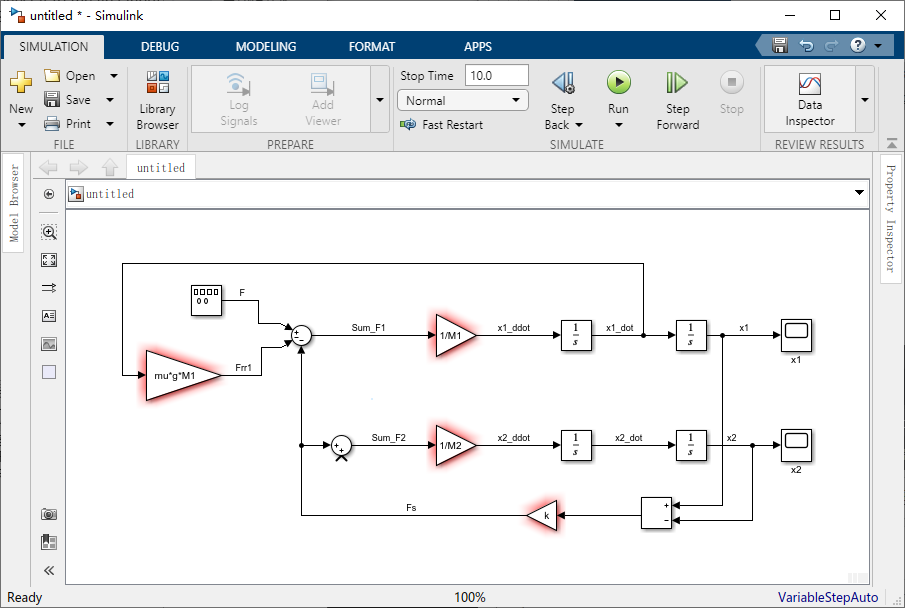
施加到车厢上的第二个力是摩擦力，该力的产生与火车头类似，注意符号为负。

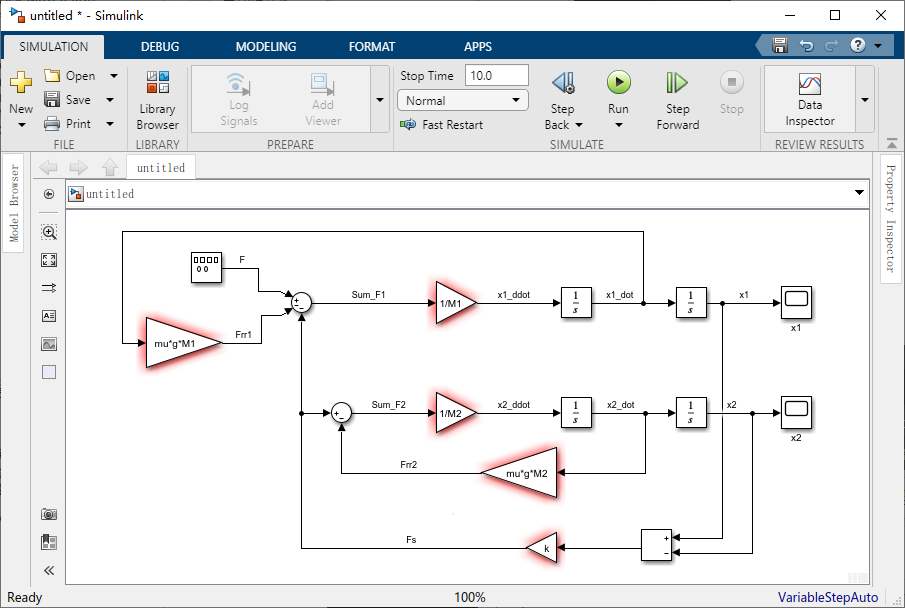
到此建模完成，我们只需要提供适当的输入并选择感兴趣的输出即可。系统的输入信号是火车头产生的力 $F$ 。在Simulink模型中，我们已经将 $F$ 定义为信号发生器模块的输出。我们将观察并最终尝试控制火车头的速度。从Sinks库向窗口中拖动一个 Scope。在 “x1_dot” 信号引出以根线，然后连接到Scope上，并标记为 x1_dot。

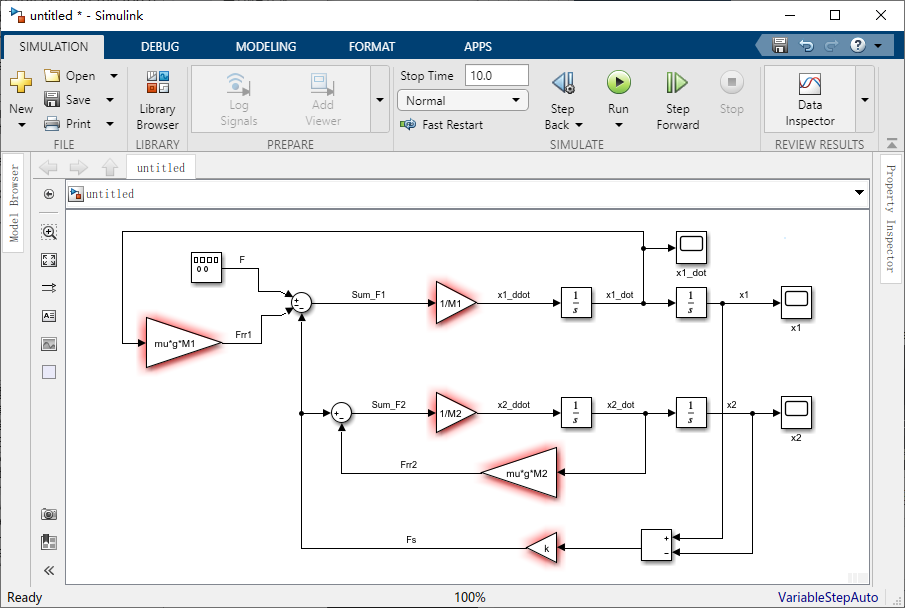
现在，模型已经完成，可以选择保存。

仿真模型

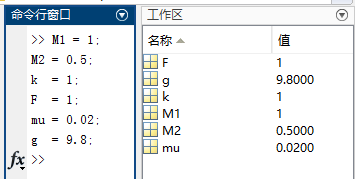
在仿真模型之前，我们需要对模型中使用的每个变量分配数值，对于火车系统，我们选择如下：

• $M_1$ = 1 kg
• $M_2$ = 0.5 kg
• $k$ = 1 N/m
• $F$ = 1 N
• $\mu$ = 0.02 s/m
• $g$ = 9.8 m/s^2

M1 = 1;
M2 = 0.5;
k  = 1;
F  = 1;
mu = 0.02;
g  = 9.8;

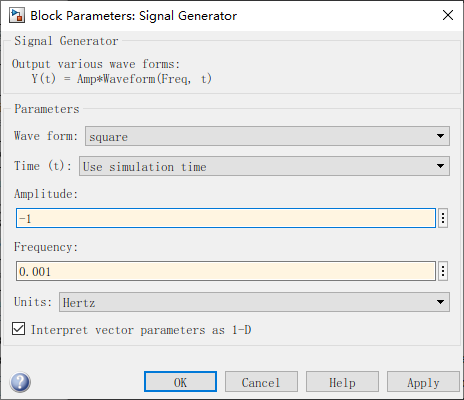
现在，我们需要为火车头提供适当的输入，双击信号发生器(输入“F”)。从“Wave form”中选择“square”，然后将“Frequency” 设置为 “0.001”，将单位设置为“Hertz”，另外还需要将 “Amplitude” 设置为 -1，注意设置为 -1 表示 方波先是正，后是负。


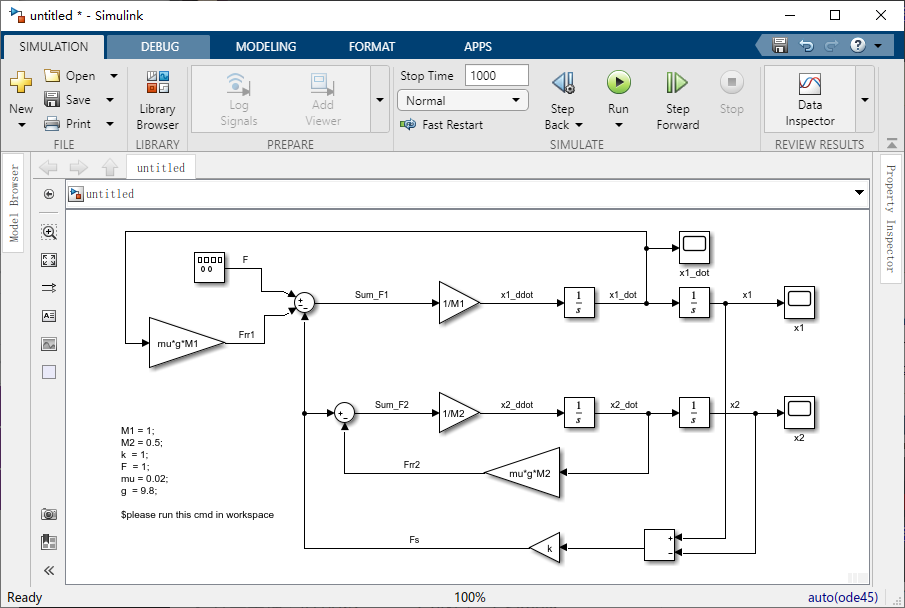
仿真运行之前的最后一个步骤选择适当的仿真时间。要查看 0.001 Hz 方波的一个周期。我们要进行 1000s 的仿真。从模型窗口的顶部将 Stop Time 设置为 1000。
现在，运行仿真，并打开 “x1_dot” ，可以看出速度先为正后为负。

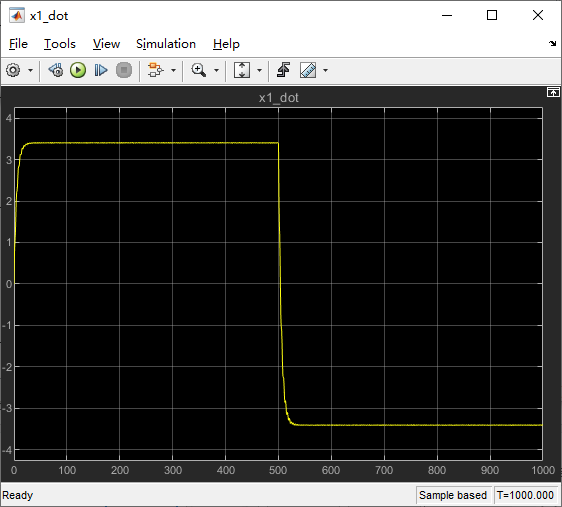
在该教程中，我们从第一部分对火车系统进行了数学建模，然后再Simulink中搭建了模型框图，现在可以用Simscape替代Simulink进行物理建模，Simscape是Simulink新增的一个工具箱，它使用户可以直接用物理的模块(例如惯性，关节，电阻器或者电感器)来对系统进行建模。使用Simuscape可使用户仿真物理系统而无需导出控制数学方程式。
下一个教程，我们将为火车系统设计控制器。

最后

以上就是认真秀发为你收集整理的控制教程 —— 介绍篇：8.基于Simulink为火车系统建模的全部内容，希望文章能够帮你解决控制教程 —— 介绍篇：8.基于Simulink为火车系统建模所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。