NR LDPC专题-01- 线性码简介

112 阅读 0 评论 74 点赞

我是靠谱客的博主感动草莓，最近开发中收集的这篇文章主要介绍NR LDPC专题-01- 线性码简介，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言：

这篇主要讲一下相关的背景知识：

LDPC是Low Density Parity Check Code英文缩写，意思是低密度奇偶校验码，最早在20世纪60年代由Gallager在他的博士论文中提出。

LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出，但限于当时的技术条件，缺乏可行的译码算法，此后的35年间基本上被人们忽略，其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示，即后来所称的Tanner图。1993年Berrou等人发现了Turbo码，在此基础上，1995年前后MacKay和Neal等人对LDPC码重新进行了研究，提出了可行的译码算法，从而进一步发现了LDPC码所具有的良好性能，迅速引起强烈反响和极大关注。经过十几年来的研究和发展，研究人员在各方面都取得了突破性的进展，LDPC码的相关技术也日趋成熟，甚至已经开始有了商业化的应用成果，并进入了无线通信等相关领域的标准。

LDPC码是通过校验矩阵定义的一类线性码，为使译码可行，在码长较长时需要校验矩阵满足“稀疏性”，即校验矩阵中1的密度比较低，也就是要求校验矩阵中1的个数远小于0的个数，并且码长越长，密度就要越低。

这里主要讲解一下相关的背景知识

线性码编码器
矩阵描述
例子 examples
最小距离 minimum Distance
最小距离和线性编码器关系 minimum Distance - Linear codes

一线性码编码器

basic of linear code

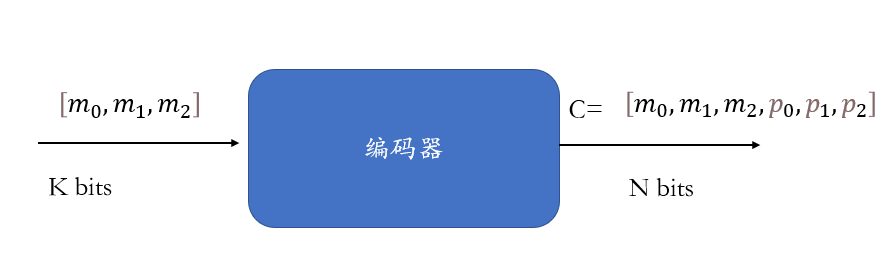
发送的消息：

一个长度为k的向量m

编码成一个codeword：

是一个长度为n 的向量 :

其中：k个为向量m, n-k个为奇偶校验位 P。

如上(6,3)code 模型: 其中奇偶校验位为

$left{begin{matrix} p_0=(m_0+m_1)mod 2\ p_1=(m_1+m_2)mod 2 \ p_2=(m_2+m_0)mod 2 end{matrix}right.$

注意这里面跟线性代数的区别，加法代表XOR，模二加法

二矩阵描述

2.1 生成矩阵（codeword generator matrix）

G=[I,P]

c= mG

I: 是单位矩阵， P为奇偶校验矩阵（实现XOR运算）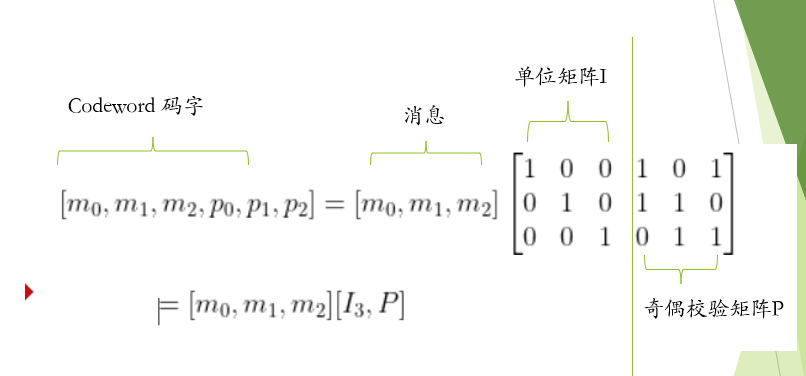

是一个单位矩阵和一个奇偶校验矩阵组成的矩阵

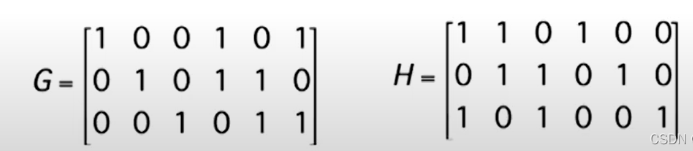
2.2 奇偶校验矩阵（parity-check matrix）

$hc^t=0$

LDPC码主要思想就这个

如下：

$begin{bmatrix} 1 & 1 & 0 &1 &0 &0 \ 0& 1 & 1 & 0 & 1 &0 \ 1& 0 & 1 &0 &0 &1 end{bmatrix}begin{bmatrix} m_0\ m_1\ m_2\ p_0\ p_1\ p_2 end{bmatrix}=begin{bmatrix} 0\ 0 \ 0 end{bmatrix}$

$[p^ti_3]c^t=0$

$h=p^t,i_3$

上面展开就是

$left{begin{matrix} m_0+m_1+p_0=0\ m_1+m_2+p_1=0 \ m_2+m_0+p_2=0 end{matrix}right.$

三例子

3.1 repetition code(3,1)

k=1,n=3,奇偶校验位两位

repetition code ={000,111}

里面有2个codeword:

$g=begin{bmatrix} 1 & 1 & 1 end{bmatrix}$

codewords:

$[000]=mg=[0]g$

$[111]=mg=[1]g$

$h=begin{bmatrix} 1 & 0 &1 \ 0 & 1 & 1 end{bmatrix}$

$=[p^t,i]$

$hc^t=0$