计算机网络系列内容的学习目录$\to$谢希仁计算机网络学习系列内容汇总。

4. 编码与调制

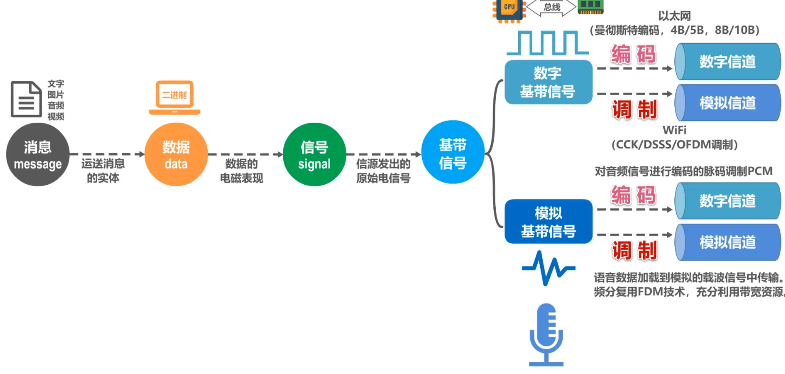
  在计算机网络中，计算机需要处理和传输用户的文字、图片、音频和视频，它们可以统称为消息。
  数据是运送消息的实体，我们比较熟悉的是十进制数据，而计算机只能处理二进制数据（即比特0和比特1）。
  计算机中的网卡将比特0和比特1变换成相应的电信号发送到网线，也就是说，信号是数据的电磁表现。
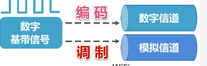
  由信源发出的原始电信号称为基带信号，基带信号可分为两类：一类是数字基带信号，例如，计算机内部CPU与内存之间传输的信号；另一类是模拟基带信号，例如，麦克风收到声音后产生的音频信号。信号需要在信道中进行传输，信道可分为数字信道和模拟信道两种。
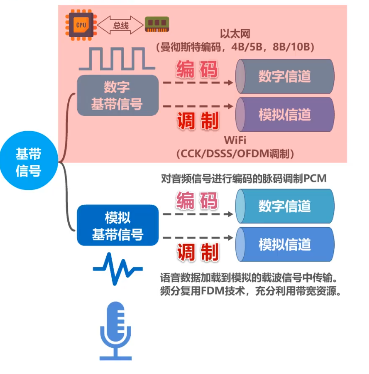
  在不改变信号性质的前提下，仅对数字基带信号的波形进行变换，称为编码。编码后产生的信号仍为数字信号，可以在数字信道中传输。例如，以太网使用曼彻斯特编码、4B/5B、8B/10B等编码，把数字基带信号的频率范围搬移到较高的频段，并转化为模拟信号，称为调制。调制后产生的信号是模拟信号，可以在模拟信道中传输。例如，WiFi使用补码键控、直接序列扩频、正交频分复用等调制方法。
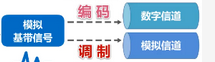
  对于模拟基带信号的处理，也有编码和调制两种方法。对模拟基带信号进行编码的典型应用是对音频信号进行编码的脉码调制PCM，也就是将模拟音频信号通过采样、量化、编码三个步骤进行数字化。对模拟基带信号进行调制的典型应用是将语音数据加载到模拟的载波信号中传输，例如传统的电话；另一个是频分复用技术，可以充分利用带宽资源。

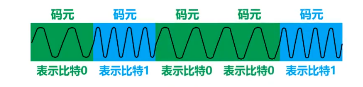
  码元： 在使用时间域的波形表示数字信号时，代表不同离散数值的基本波形。

  传输媒体与信道的关系： 严格来说，传输媒体与信道不能直接划等号。对于单工传输，传输媒体中只包含一个信道，要么是发送信道，要么是接受信道。

  对于半双工和全双工传输，传输媒体中要包含两个信道，一个是发送信道，另一个是接受信道。

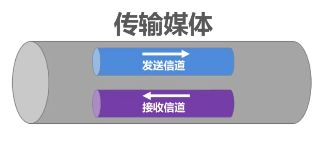
  如果使用信道复用技术。一条传输媒体还可以包含多个信道。
  在计算机网络中，常见的是将数字基带信号通过编码或调制的方法在相应通道进行传输。

4.1 常用编码

  几种常用编码： 不归零编码、归零编码、曼彻斯特编码、差分曼彻斯特编码。

• 不归零编码
    所谓“不归零”，是指在整个码元时间内，电平不会出现零电平。
   
   
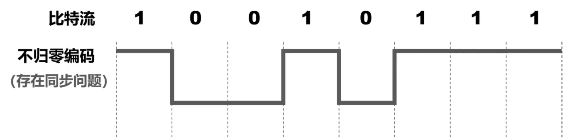
    问题： 接收端如何判断几个码元？
   
   
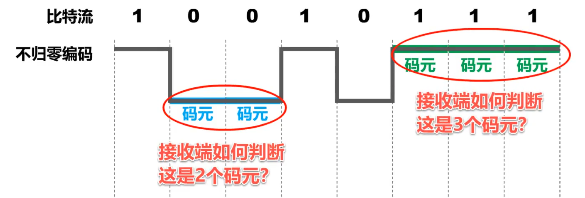
    需要额外一根传输线来传输时钟信号，使发送方和接收方同步。
    对于计算机网络，宁愿利用这根传输线传输数据信号，而不是传输时钟信号！

• 归零编码
   
   
    每个码元传输结束后信号都要“归零”，所以接收方只要在信号归零后进行采样即可，不需要单独的时钟信号。
    实际上，归零编码相当于把时钟信号用“归零”方式编码在了数据之内，这称为“自同步”信号。
    但是，归零编码中大部分的数据带宽，都用来传输“归零”而浪费掉了。

• 曼彻斯特编码
   
   
    在每个码元时间的中间时刻，信号都会发生跳变。码元中间时刻的跳变既表示时钟，又表示数据。

• 差分曼彻斯特编码
   
   
    在每个码元时间的中间时刻，信号都会发生跳变。与曼彻斯特编码不同，跳变仅表示时钟，用码元开始处电平是否发生变化表示数据。

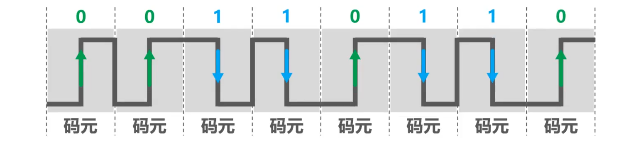
  例： 若下图为10BaseT网卡接收到的信号波形，则该网卡收到的比特串是( A )

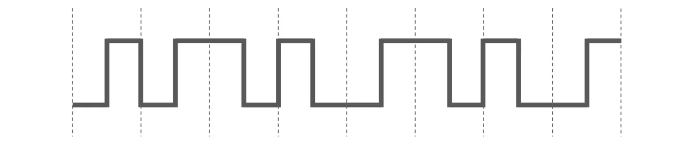
     A. 0011 0110  B. 1010 1101  C. 0101 0010  D. 1100 0101
    分析： 1. 10BaseT以太网使用的是曼彻斯特编码；
        2. 每个码元在中间时刻跳变，按此特点找出每个码元；
        3. 正跳变表示1还是0，负跳变表示0还是1，可自行假设。
        假设正跳变表示1，负跳变表示0，该网卡收到的比特串如下图所示，没有正确答案。

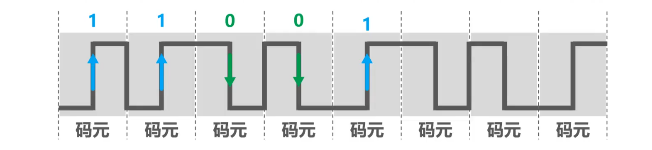
        假设正跳变表示0，负跳变表示1，该网卡收到的比特串如下图所示，为 0011 0110。

4.2 基本调制方法

  下图是待传输的数字基带信号，也就是来自信源的原始数字信号。我们要使用模拟信道来传输，因此需要将数字基带信号通过调制方法调制成可以在模拟信道中传输的模拟信号。

  下图是调幅所产生的模拟信号。无载波输出表示比特0，有载波输出表示比特1。

  下图是调频所产生的模拟信号。频率f1的波形表示比特0，频率f2的波形表示比特1。

  下图是调相所产生的模拟信号。初相位0度的波形表示比特0，初相位180度的波形表示比特1。

  使用基本调制方法，1个码元只能包含1个比特信息。如何能使1个码元包含更多的比特呢?
  可以采用混合调制的方法。

4.3 混合调制

  因为频率和相位是相关的，即频率是相位随时间的变化率。所以一次只能调制频率和相位两个中的一个。
  通常情况下，相位和振幅可以结合起来一起调制，称为正交振幅调制 QAM。

  混合调制举例——正交振幅调制QAM
  QAM-16：12种相位
       每种相位有1或2种振幅可选
       可以调制出16种码元(波形)，每种码元可以对应表示4个比特
       码元与4个比特的对应关系采用格雷码，任意两个相邻码元只有1个比特不同。

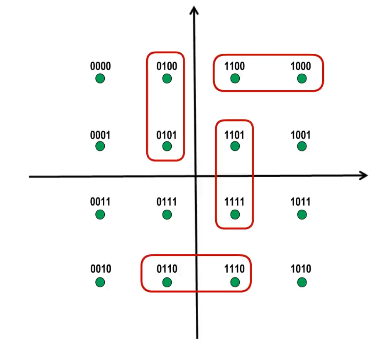
  码元是指在使用时间域的波形表示数字信号时，代表不同离散数值的基本波形。简单来说，码元就是一段调制好的基本波形，可以表示比特信息。

4.4 课后练习

  1. 数字基带信号通过( D )后可在模拟信道进行传输
    A. 编码  B. 解调   C. 滤波   D. 调制
   分析： 把数字基带信号的频率范围搬移到较高的频段，并转化为模拟信号，称为调制。数字基带信号通过调制后可在模拟信道进行传输。

  2. 模拟基带信号通过( A )后可在数字信道进行传输
    A. 编码  B. 解调   C. 滤波   D. 调制
   分析： 模拟基带信号通过编码后可在数字信道进行传输。

  3. 不含同步信息的编码是( A )
    I. 不归零编码   II. 曼彻斯特编码   III. 差分曼彻斯特编码
    A. 仅I  B. 仅II   C. 仅II、III   D. I、II、III
   分析： 非归零码是最简单的一种编码方法，它用低电平表示0，高电平表示1；或者反过来。由于每个码元之间并没有间隔标志，因此它不包含同步信息。
       曼彻斯特编码和差分曼彻斯特编码都是将每个码元分成两个相等的时间间隔，将每个码元的中间跳变作为收发双方的同步信号，所以无需额外的同步信号，实际应用得较多，但它们所占的频带宽度是原始的基带宽度的2倍。

  4. 下图所示为某比特串的曼彻斯特编码信号波形，则该比特串为( A )
    A. 0011 0110  B. 1010 1101   C. 0101 0010   D. 1100 0101
   分析： 假设正跳变表示0，负跳变表示1，该网卡收到的比特串如下图所示，为 0011 0110。

  5. 若某通信链路的数据传输率为4800b/s，采用8相位调制，则该链路的波特率是( C )
    A. 600Baud  B. 1200Baud   C. 1600Baud   D. 3200Baud
   分析： 已知采用8个相位，即可以表示8种状态，所以一个码元可以携带 2bit （2${}^3$=8）的信息。根据比特率（或者称为数据传输速率）和波特率的关系，假设每个码元可以携带n位信息，则比特率=n×波特率，由题意可知，比特率为4800bit/s，且n=3，所以波特率为1600Baud。

  6. 采用8种相位，每种相位各有2种幅度的QAM调制方法，在1200Baud的信号传输速率下能达到的数据传输率为( C )
    A. 2400b/s  B. 3600b/s   C. 4800b/s   D. 9600b/s
   分析： 已知N=8，采用QAM调制方法，每种相位各有2种幅度，可以得到8 $\ast$ 2=16状态。根据数据传输速率与调制速率的的关系：S=B $\ast$ log2(N)=1200 $\ast$ log2(16) =1200 $\ast$ 4=4800b/s。

5. 信道的极限容量

  下图所示是一个数字信号，当它通过实际的信道后，波形会产生失真。当失真不严重时，在输出端还可根据已失真的波形还原出发送的码元。但当失真严重时，在输出端就很难判断这个信号在什么时候是1和在什么时候是0，信号波形失去了码元之间的清晰界限，这种现象叫做码间串扰。

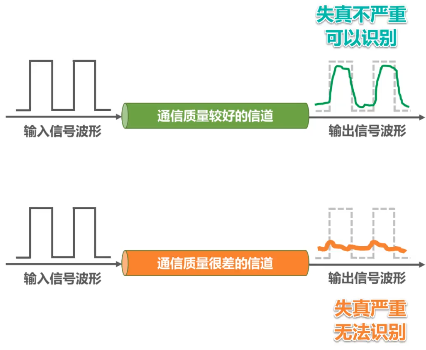
  产生失真的原因主要有： 1. 码元传输速率；
              2. 信号传输距离；
              3. 噪声干扰；
              4. 传输媒体质量。

5.1 奈氏准则

  奈氏准则： 在假定的理想条件下，为了避免码间串扰，码元传输速率是有上限的。
        理想低通信道的最高码元传输速率 = 2W Baud = 2W码元/秒。
        理想带通信道的最高码元传输速率 = W Baud = W码元/秒。
        其中，W为信道带宽(单位为Hz)；Baud为波特，即码元/秒。

  $\star$ 码元传输速率又称为波特率、调制速率、波形速率或符号速率。它与比特率有一定关系：
   $\diamond$ 当1个码元只携带1比特的信息量时，则波特率（码元/秒)与比特率（比特/秒)在数值上是相等的；
   $\diamond$ 当1个码元携带n比特的信息量时，则波特率转换成比特率时，数值要乘以n。
  $\star$ 要提高信息传输速率（比特率)，就必须设法使每一个码元能携带更多个比特的信息量，这需要采用多元制。
   $\diamond$ 之间的调幅、调频、调相三种基本调制方法，均属于二元调制，只能产生两种不同的码元，也就是两种不同的基本波形，因此每个码元只能携带1比特的信息量。而混合调制属于多元调制，例如QAM16可以调制出16种不同的码元，因此每个码元可以携带4比特的信息量。
  $\star$ 实际的信道所能传输的最高码元速率，要明显低于奈氏准则给出的这个上限数值。（这是因为奈氏准则是在假定的理想条件下推导出来的，不考虑其他因素，例如传输距离、噪声干扰、传输媒体质量等。）

  思考： 只要采用更好的调制方法，让码元可以携带更多的比特，岂不是可以无限制地提高信息的传输速率?
  答案是否定的。因为信道的极限信息传输速率还要受限于实际的信号在信道中传输时的信噪比。

5.2 香农公式

  香农公式： 带宽受限且有高斯白噪声干扰的信道的极限信息传输速率。
$$c=W\times lo{g}_2(1+\frac{S}{N})$$  其中， C为信道的极限信息传输速率(单位：b/s)；
      W为信道带宽（单位：Hz)；
      S为信道内所传信号的平均功率；
      N为信道内的高斯噪声功率；
      S/N为信噪比，使用分贝(dB)作为度量单位，
        信噪比(dB) = $10\times lo{g}_{10}(\frac{S}{N})$(dB)。

  $\star$ 信道带宽或信道中信噪比越大，信息的极限传输速率越高。
  $\star$ 在实际信道上能够达到的信息传输速率要比该公式的极限传输速率低不少。这是因为在实际信道中，信号还要受到其他一些损伤，如各种脉冲干扰、信号在传输中的衰减和失真等，这些因素在香农公式中并未考虑。

5.3 奈氏准则和香农公式的意义

  1. 在信道带宽一定的情况下，根据奈氏准则和香农公式，要想提高信息的传输速率就必须采用多元制(更好的调制方法)和努力提高信道中的信噪比。
  2. 自从香农公式发表后，各种新的信号处理和调制方法就不断出现，其目的都是为了尽可能地接近香农公式给出的传输速率极限。

  例1： 下列因素中，不会影响信道数据传输速率的是( D )
      A. 信噪比  B. 频率带宽  C. f调制速度  D. 信号传播速度
     分析： 从香农公式可知，信噪比、频率带宽都会影响信道数据传输速率。从奈氏准则可知，调制速度（即码元传输速度）、码元所携带的比特数量都会影响信道数据传输速率。而信号的传播速度不影响信道数据传输速率。

  例2： 在无噪声情况下，若某通信链路的带宽为3kHz，采用4个相位，每个相位具有4种振幅的QAM调制技术，则该通信链路的最大数据传输速率是( B )
      A. 12 kbps  B. 24 kbps  C. 48 kbps  D. 96 kbps
     分析： (1) 根据奈氏准则可知，该通信链路的最高码元传输速率 = 2 $\times$ 3k = 6k(Baud) = 6k(码元/秒)；
         (2) 采用4个相位，每个相位4种振幅的QAM调制技术，可以调制出4 $\times$ 4 = 16个不同的基本波形（码元)；
            采用二进制对这16个不同的码元进行编码，需要使用4个比特($lo{g}_{2}16$ = 4)。换句话说，每个码元可以携带的信息量为4比特；
         综合(1)和(2)可知，该通信链路的最大数据传输速率 = 6k(码元/秒) $\times$ 4(比特/码元) = 24k(比特/秒) = 24 kbps。

  例3： 若某通信链路的数据传输速率为2400bps，采用4相位调制，则该链路的波特率是( B )
      A. 600波特  B. 1200波特  C. 4800波特  D.9600波特
     分析： (1) 采用4相位调制，可以调制出4种相位不同的基本波形（码元)。采用二进制对这4个不同的码元进行编码，
需要使用2个比特($lo{g}_{2}4$ = 2)。换句话说，每个码元可以携带的信息量为2比特；
         (2) 数据传输速率 = 波特率(码元传输速率)$\times$每个码元所携带的信息量
            2400(比特/秒) = 波特率 $\times$ 2 (比特/码元)
            解得：波特率 = 1200(码元/秒) = 1200(Baud) =1200(波特)。

  例4： 若连接R2和R3链路的频率带宽为8kHz，信噪比为30dB，该链路实际数据传输速率约为理论最大数据传输速率的50%，则该链路的实际数据传输速率约是( C )
      A. 8 kbps  B. 20 kbps  C. 40 kbps  D. 80 kbps
     分析： 理论最大数据传输速率 $c=8k\times lo{g}_2(1+\frac{S}{N})$
         $30(dB)=10\times lo{g}_{10}(\frac{S}{N})(dB)$ 解得$\frac{S}{N}$ = 1000 代入上式
         $c=8k\times lo{g}_2(1+1000)\approx 80kbps$
         该链路的实际数据传输速率 $c\times 50$% $=40kbps$。

  例5： 若信道在无噪声情况下的极限数据传输速率不小于信噪比为30dB条件下的极限数据传输速率，则信号状态数至少是( D ）
      A. 4  B. 8  C. 16  D. 32
     分析： 设信号状态数（即可调制出的不同基本波形或码元数量)为X
         则每个码元可携带的比特数量为$lo{g}_{2}X$
         信道在无噪声情况下的极限数据传输速率(用奈氏准则计算) = 2W(码元/秒)= 2W $lo{g}_{2}X$(比特/秒)
         30dB信噪比条件下的极限数据传输速率(用香农公式计算) = W $lo{g}_2(1+1000)$(比特/秒)
         根据题意列出不等式：2W $lo{g}_{2}X$ > W $lo{g}_2(1+1000)$ 解得x ≥ 32

5.4 课后练习

  1. 影响信道最大传输速率的因素主要有( A ）
    A. 信道带宽和信噪比  B. 码元传输速率和噪声功率  C. 频率特性和带宽   D. 发送功率和噪声功率
   分析： 从香农公式可知，信噪比、频率带宽都会影响信道数据传输速率。从奈氏准则可知，调制速度（即码元传输速度）、码元所携带的比特数量都会影响信道数据传输速率。

  2. 在无噪声情况下，若某通信链路的带宽为4kHz，采用8个相位的调制技术，则该通信链路的最大数据传输速率是( B ）
    A. 12kbps  B. 24kbps率  C. 48kbps   D. 96kbps
   分析： (1) 根据奈氏准则可知，该通信链路的最高码元传输速率 = 2 $\times$ 4k = 8k(Baud) = 8k(码元/秒)；
       (2) 采用8个相位的调制技术，可以调制出8个不同的基本波形（码元)；
          采用二进制对这8个不同的码元进行编码，需要使用3个比特($lo{g}_{2}8$ = 3)。换句话说，每个码元可以携带的信息量为3比特；
       综合(1)和(2)可知，该通信链路的最大数据传输速率 = 8k(码元/秒) $\times$ 3(比特/码元) = 24k(比特/秒) = 24 kbps。

  3. 若链路的频率带宽为4kHz，信噪比为30dB，则该链路的理论最大数据传输速率是( A ）
    A. 40kbps  B. 80kbps率  C. 120kbps   D. 160kbps
   分析： 理论最大数据传输速率 $c=4k\times lo{g}_2(1+\frac{S}{N})$
       $30(dB)=10\times lo{g}_{10}(\frac{S}{N})(dB)$ 解得$\frac{S}{N}$ = 1000 代入上式
       $c=4k\times lo{g}_2(1+1000)\approx 40kbps$。

最后

以上就是无奈冰棍为你收集整理的计算机网络（二）—— 物理层（4、5）：编码与调制、信道的极限容量4. 编码与调制5. 信道的极限容量的全部内容，希望文章能够帮你解决计算机网络（二）—— 物理层（4、5）：编码与调制、信道的极限容量4. 编码与调制5. 信道的极限容量所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。