文章目录
- 0.什么是机器学习
- 1.线性回归
- 1.1最小二乘
- 1.2梯度下降
- 1.3梯度下降法-一元线性回归
0.什么是机器学习
机器学习(machine learning)是目前信息技术中最激动人心的方向之一,通过学习机器学习我们可以深入了解人类的本质(复读机??)——人类学习的过程,可以在一定程度上帮助我们了解学习的机制,提升我们日常工作的效率.
机器学习的本质是通过不断学习大量知识求解一个具体问题,而这个大量的知识我们称之为训练集,再通过验证集进行评估学习(模型)的好坏,这类似于我们学习数学一样,在考试前疯狂的做题目进行训练,再通过考试验证自己是否掌握了这些知识。
1.线性回归
以房价数据为例
| size | price |
|---|---|
| 100 | 100000 |
| 200 | 240000 |
| 300 | 300000 |
影响房价的因素我们称之为特征(feature)
而房价我们称之为标签(target)
简化的房价求解方程如下:
f
(
x
)
=
θ
0
+
θ
1
∗
x
f(x) = theta_0+theta_1*x
f(x)=θ0+θ1∗x
代价函数(cost function)又称损失函数,用于评价模型的好坏,用于计算feature
常见的代价函数有最小二乘
1.1最小二乘
真实值y,误差值
h
θ
(
x
)
h_theta(x)
hθ(x),则误差为
(
y
−
h
θ
(
x
)
)
2
(y-h_theta(x))^2
(y−hθ(x))2
Γ
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
y
i
−
h
θ
(
x
i
)
)
2
Gamma(theta_0,theta_1) = frac{1}{2m}sum_{i=1}^{m}(y^i-h_theta(x^i))^2
Γ(θ0,θ1)=2m1i=1∑m(yi−hθ(xi))2
使该函数最小
相关系数
我们使用相关系数去衡量线性相关性的强弱
r
x
y
=
∑
(
x
i
−
x
ˉ
)
(
y
i
−
y
ˉ
)
∑
(
x
i
−
x
ˉ
)
2
∑
(
y
i
−
y
ˉ
)
2
r_{xy}= frac{sum(x_i-bar{x})(y_i-bar{y})}{sqrt{sum(x_i-bar{x})^2sum(y_i-bar{y})^2}}
rxy=∑(xi−xˉ)2∑(yi−yˉ)2∑(xi−xˉ)(yi−yˉ)
x
ˉ
bar{x}
xˉ代表所有x的平均值
相关系数越接近1表示这些样本点越接近线性的关系
决定系数
总平方和(SST):
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
sum_{i=1}^{n}(y_i-bar{y})^2
∑i=1n(yi−yˉ)2
回归平方和(SSR):
∑
i
=
1
n
(
y
^
−
y
ˉ
)
2
sum_{i=1}^{n}(widehat{y}-bar{y})^2
∑i=1n(y
−yˉ)2
残差平方和(SSE):
∑
i
=
1
n
(
y
i
−
y
^
)
2
sum_{i=1}^{n}(y_i-widehat{y})^2
∑i=1n(yi−y
)2
三者关系:SST=SSR+SSE
决定系数:
R
2
=
S
S
R
S
S
T
=
1
−
S
S
E
S
S
T
R^2=frac{SSR}{SST}=1-frac{SSE}{SST}
R2=SSTSSR=1−SSTSSE
决定系数越接近1表示变量之间越接近线性的关系
1.2梯度下降
梯度下降算法用于优化代价函数,使得代价函数不断减小达到最小值
Have some function
Γ
(
θ
0
,
θ
1
)
Gamma(theta_0,theta_1)
Γ(θ0,θ1)
What
min
θ
0
,
θ
1
Γ
(
θ
0
,
θ
1
)
min_{theta_0,theta_1}Gamma(theta_0,theta_1)
minθ0,θ1Γ(θ0,θ1)
- 初始化 θ 0 , θ 1 theta_0,theta_1 θ0,θ1
- 不断改变
θ
0
,
θ
1
theta_0,theta_1
θ0,θ1,直到
Γ
(
θ
0
,
θ
1
)
Gamma(theta_0,theta_1)
Γ(θ0,θ1)到达全局最小或者局部最小
θ j : = θ j − α ∂ ∂ θ j Γ ( θ 0 , θ 1 ) ( f o r j = 0 1 a n d 1 j = 1 ) theta_j:=theta_j-alpha frac{partial }{partial theta_j}Gamma(theta_0,theta_1)(for j=0 hphantom{1} and hphantom{1} j=1) θj:=θj−α∂θj∂Γ(θ0,θ1)(forj=01and1j=1)
α alpha α为学习率
偏导讲解
1.3梯度下降法-一元线性回归
波士顿房价预测
import numpy as np
import matplotlib.pyplot as plt
#数据载入
data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()
# 学习率
a = 0.001
# 截距
b = 0
# 斜率
feature = 0
# 最大迭代次数
MAX_ITER = 100
# 最小误差
MIN_ERROR = 0.01
# 最小二乘
def min_plus(b,feature,x_data,y_data):
total_sum = 0
count = len(x_data)
for i in range(count):
total_sum = (y_data[i]-(b+feature*x_data[i]))**2
return 1/(2*count)*total_sum
# 梯度下降
def gradient_descent(b,feature,x_data,y_data,a=0.0001,MAX_ITER = 100,MIN_ERROR = 0.01):
count = len(x_data)
for c in range(MAX_ITER):
b_grad = 0
c_grad = 0
for i in range(count):
b_grad += (b+feature*x_data[i]-y_data[i])/count
c_grad += x_data[i]*(b+feature*x_data[i]-y_data[i])/count
b = b-a*b_grad
feature = feature-a*c_grad
return b,feature
print("Starting b = {0}, k = {1}, error = {2}".format(b,feature, min_plus(b, feature, x_data, y_data)))
print("Running...")
b, feature = gradient_descent(b, feature,x_data, y_data)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(100, b, feature,min_plus(b, feature, x_data, y_data)))
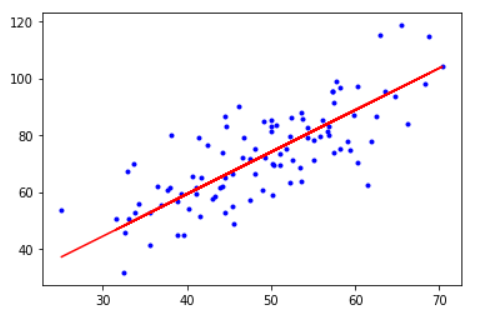
# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, feature*x_data + b, 'r')
plt.show()
Starting b = 0, k = 0, error = 14.286861304383226
Running...
After 100 iterations b = 0.032071915131595685, k = 1.4788617416703924, error = 1.3220628355160366
最后
以上就是着急镜子最近收集整理的关于机器学习——Day1的全部内容,更多相关机器学习——Day1内容请搜索靠谱客的其他文章。








发表评论 取消回复