PCA(主成分分析)通过对原始数据特征的线性组合,在尽可能保留样本之间差异性(样本方差)的情况下,形成新的特征,是最常见的数据降维手段。
t-SNE(t-distributed stochastic neighbor embedding)是一种非线性的数据降维方法,它将数据点之间的空间距离转化为相似度的概率分布(高维空间中使用高斯分布,低维空间中使用t-分布),通过最小化高维空间和低维空间概率分布的KL散度,获得数据在低维空间中的近似。通常用于高维数据的可视化。
本文分别使用t-SNE和PCA对mnist图像数据进行降维处理,再对降维后的数据进行KMeans聚类,对比其降维效果的差异。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
data, labels = load_digits(return_X_y=True)
# 加载mnist数据
(n_samples, n_features), n_digits = data.shape, np.unique(labels).size
fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6))
for idx, ax in enumerate(axs.ravel()):
ax.imshow(data[idx].reshape((8, 8)), cmap=plt.cm.binary)
ax.axis("off")
_ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16)
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler, MinMaxScaler
n_components = 2
random_state = 0
def plot_data(X, title):
'''在二维图像绘制降维后的数据
'''
fig, ax = plt.subplots()
X = MinMaxScaler().fit_transform(X)
for digit in np.unique(labels):
ax.scatter(
*X[labels == digit].T,
marker=f"${digit}$",
s=60,
color=plt.cm.Paired(digit)
)
data = StandardScaler().fit_transform(data)
# 分别使用tsne和pca进行数据降维,并将降维后的数据在散点图上显示。
pca_data = PCA(
n_components=n_components,
random_state=random_state
).fit_transform(data)
plot_data(pca_data, "PCA")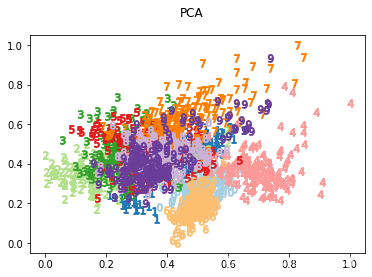
不同数字的数据点在图上显示为不同颜色,可以看到不同数字的区域在一定程度上分离开,但是仍然存在混合比较严重的区域。说明经过PCA保留的二维特征并不能很好地将所有数字区分开来。
tsne_data = TSNE(
n_components=n_components,
random_state=random_state,
n_jobs=2
).fit_transform(data)
plot_data(tsne_data, "t-SNE")
可以看到经t-SNE降维后的数据,实现非常好的分离。这也是为何t-SNE会成为多维数据可视化的首选。那么经过降维的数据在聚类时的表现如何呢?
# 使用KMeans对降维后的数据进行聚类,并使用数据的真实标签对聚类结果进行评估。降维前的数据作为参照。
from sklearn import metrics
datasets = {"no processing": data, "2-component pca": pca_data, "2-component tsne": tsne_data}
print(62 * "_")
print("datattthomotcompltv_meastARItAMI")
for name, d in datasets.items():
kmeans = KMeans(
n_clusters=n_digits,
init="k-means++",
n_init=4,
random_state=random_state
)
kmeans.fit(d)
clustering_metrics = [
metrics.homogeneity_score,
metrics.completeness_score,
metrics.v_measure_score,
metrics.adjusted_rand_score,
metrics.adjusted_mutual_info_score
]
results = [name]
results += [m(labels, kmeans.labels_) for m in clustering_metrics]
formatter_result = (
"{:18s}t{:.3f}t{:.3f}t{:.3f}t{:.3f}t{:.3f}"
)
print(formatter_result.format(*results))
print(62 * "_")结果如下:
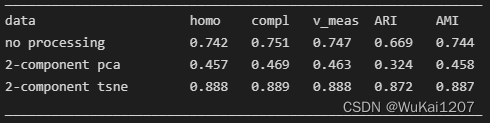
可以看到,经过PCA处理保留两个主成分的数据,聚类的结果比原始数据要差,有点意外的是,经过t-SNE处理后的降维数据,聚类结果不仅优于PCA,也优于原始数据。
考虑到二维数据表示可能并非PCA的擅场,如果增加保留的主成分,PCA理论上应该表现更好,所以在2~9范围内改变降维后的维数,用降维后的数据进行KMeans聚类,并使用Adjusted rand score评估聚类结果。
n_range = np.arange(start=2, stop=10, step=1)
ari_tsne = []
ari_pca = []
for n in n_range:
tsne_data = TSNE(
n_components=n,
random_state=random_state,
n_jobs=2,
method="exact"
# 计算梯度的方法需要设置为exact,因为默认的barnes_hut方法不支持3个以上的n_components
).fit_transform(data)
kmeans = KMeans(
n_clusters=n_digits,
init="k-means++",
n_init=4,
random_state=random_state
).fit(tsne_data)
ari_tsne.append(metrics.adjusted_rand_score(labels, kmeans.labels_))
pca_data = PCA(
n_components=n,
random_state=random_state,
).fit_transform(data)
kmeans = KMeans(
n_clusters=n_digits,
init="k-means++",
n_init=4,
random_state=random_state
).fit(pca_data)
ari_pca.append(metrics.adjusted_rand_score(labels, kmeans.labels_))
plt.plot(n_range, ari_pca, label="PCA")
plt.plot(n_range, ari_tsne, label="t-SNE")
plt.ylabel("ARI")
plt.xlabel("n_components")
plt.title("PCA vs t-SNE in clustering")
plt.legend()
plt.show()结果如下,
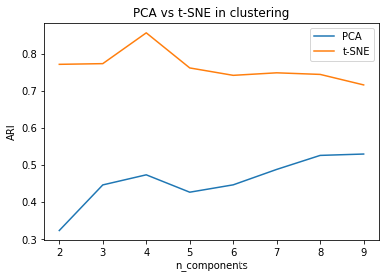
可见,随着保留的主成分增加,PCA的表现确实有所提升,而t-SNE甚至略有下降。而且相比PCA,t-SNE的计算速度极慢,且结果有一定随机性。综合来看,t-SNE非常适合用于数据降维到2维、3维,进行可视化,对于某些无监督学习问题,可以作为一种数据预处理的手段,有时能起到意料之外的效果。
最后
以上就是淡定篮球最近收集整理的关于t-SNE和PCA进行数据降维和聚类的比较的全部内容,更多相关t-SNE和PCA进行数据降维和聚类内容请搜索靠谱客的其他文章。








发表评论 取消回复