目录
1、概述
1.1、信道模型
1.2、调制信道模型
1.3、信道参数和影响因素
2、不考虑空间特性的信道模型(全向天线)
2.1、信道的基本特质
2.1.1、多经
2.1.2、多普勒频移(Doppler Shift)
2.2.3、衰落计算实列(基于射线追踪的)
2.2.4、平坦衰落信道(基于随机信道分布函数的)
2.2、传播预测模型
2.2.1、Hata模型
2.2.2、IMT-2000室内路径损耗模型
2.2.3、其他路径损耗模型
2.3、信道冲激响应
2.3.1、IMT-2000信道模型
2.3.2、多普勒功率谱
2.3.3、多径时延主要参数
2.4、信道响应理论模型
2.4.1、冲激响应
2.4.2、扩展函数和时变传输函数
2.4.3、随机模型(冲激响应的相关函数)
2.4.4、相干时间和相干带宽
3、考虑空间特性的信道模型(方向性天线)
3.1、有到达角的信道模型
3.2、平均AOA和角度扩展
3.3、同性质信道(Homogeneous Channels)
4、信道仿真模型
4.1、宏小区基站
4.2、Lee模型
4.3、典型城市仿真模型
4.4、恶劣城市仿真模型
1、概述
1.1、信道模型
信道是以媒质为基础的信号通道。
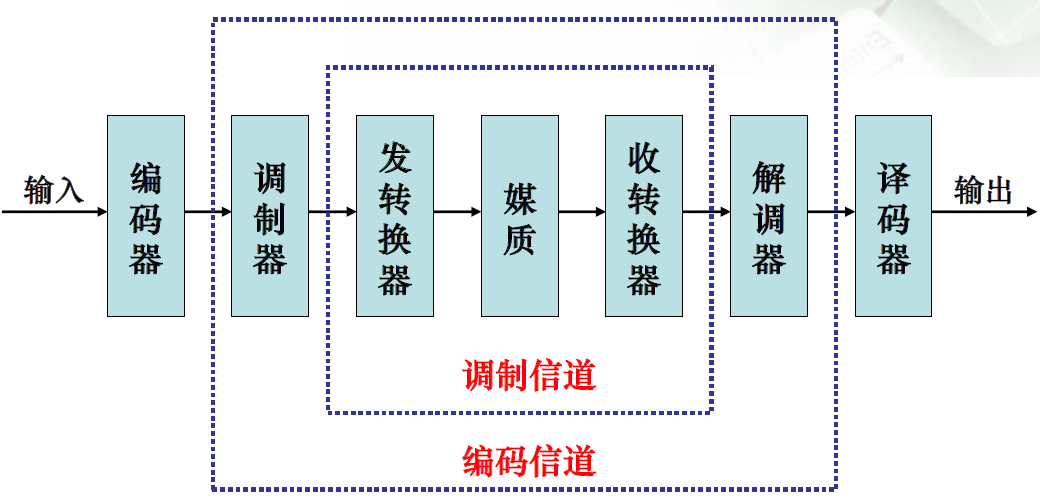
编码译码器间即为编码信道,调制解调器间即为调制信道。
1.2、调制信道模型
解调器接收信号可以看成输入为调制器的线性时变网络的输出和加性白噪声的和信号,即
,

其中,f[ ]反映了信道特征,由于是线性信道,有
,
c(t)为信道单位冲激响应。
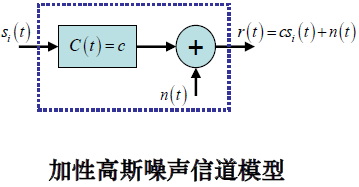
a) 加性高斯噪声信道模型(信道冲激函数是常数)
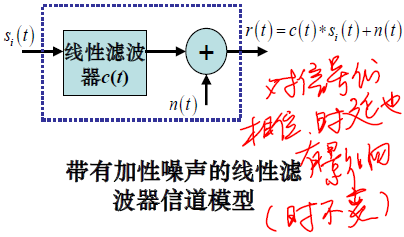
b) 带有加性噪声的线性滤波器信道(信道冲激函数不随时间变化)
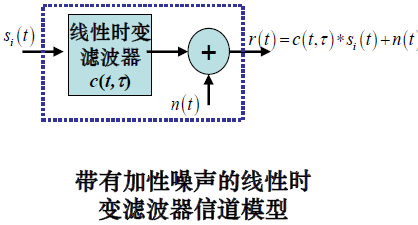
c) 带有加性噪声的线性时变滤波器信道(信道冲激函数随时间变化)
1.3、信道参数和影响因素
a) 弥散损耗(自由空间损耗):随传播距离产生的损耗。
b) 阴影效应(Shadow Fading):受地形、建筑物遮蔽产生,与传播距离无关。
c) 电平快衰落和时延拓展(多径效应产生):多径信号的幅度、相位和到达时间不同,相互叠加产生。
d) 随机调频(多普勒频移产生):快速移动导致的多普勒频移产生随机调频。
2、不考虑空间特性的信道模型(全向天线)
2.1、信道的基本特质
2.1.1、多经
多径产生原因:移动通信采用300M~10GHz频段(军事采用30~30MHz,也有毫米波),波长10m,比大型遮挡物要小得多,所以电磁波主要以直射、反射、散射、绕射(衍射)为主,接收信号因此包含多个路径的发射信息,从而产生多径。
- LOS:直射波:功率上明显大于其他(如果接收到);
- NLOS:反射(Reflect,障碍物尺寸大于
)和绕射(Diffract,障碍物尺寸小于
):都是大物体的影响;
- 散射(Scattering):信号遇到凹凸不平的表面。
多径后果——快衰落:不同路径信号大体相互独立且随机,因此接收信号可能是同相叠加增强也可能是反相相消减弱,随着距离的变化也会产生这种情况,导致了接收信号在时域和空域急剧变化,这种变化被称为快衰落。
2.1.2、多普勒频移(Doppler Shift)
发射台或接收台和/或信道中其他物体运动造成。
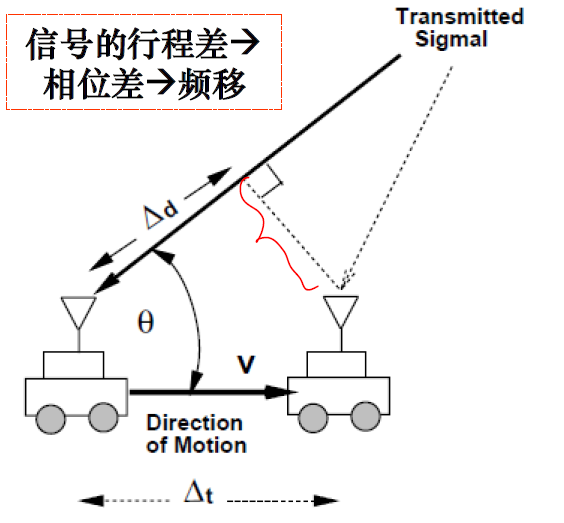
.
2.2.3、衰落计算实列(基于射线追踪的)
a) 功率推导
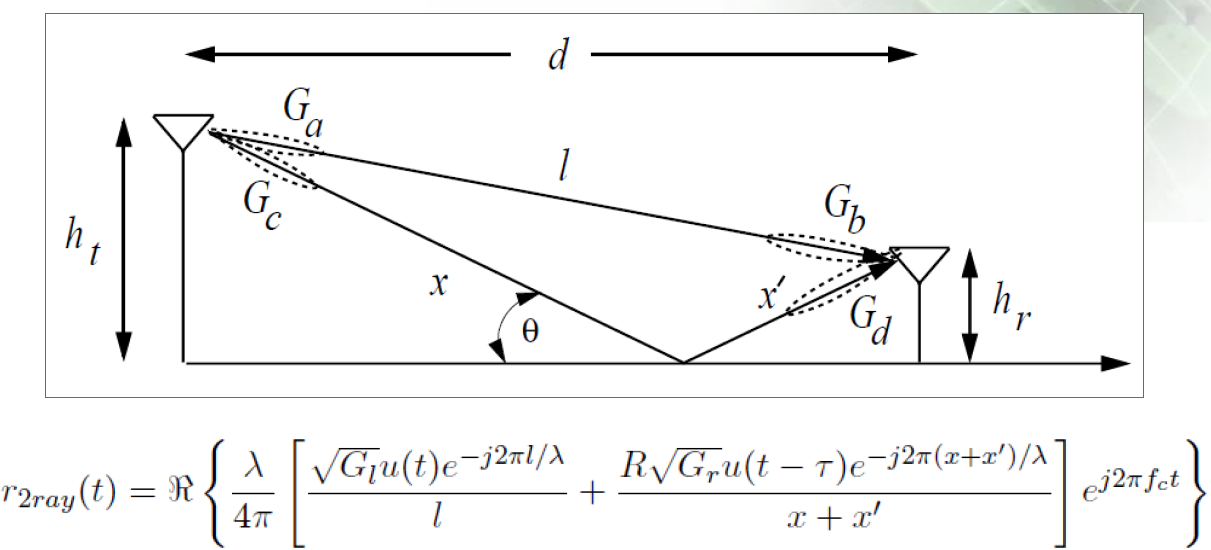 ,
,
其中,是直视路径天线增益,
是反射路径天线增益,
是反射波对直射波的时延,R是地面反射系数,忽略反射面的损耗。
如果发射信号相对时延扩展是窄带的(,即
),接收信号功率为:
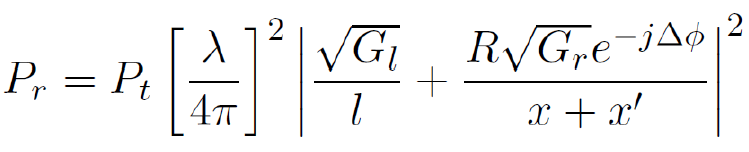 ,
,
其中,相位差
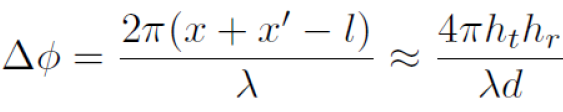 .
.
进一步地,如果有,
,
(没有吸收),则有接收功率
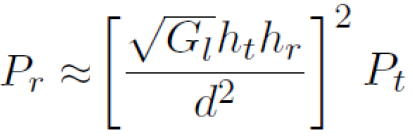 .
.
b) 仿真结果
设定参数如下,可以得到宏小区的接收信号功率和距离的仿真结果:
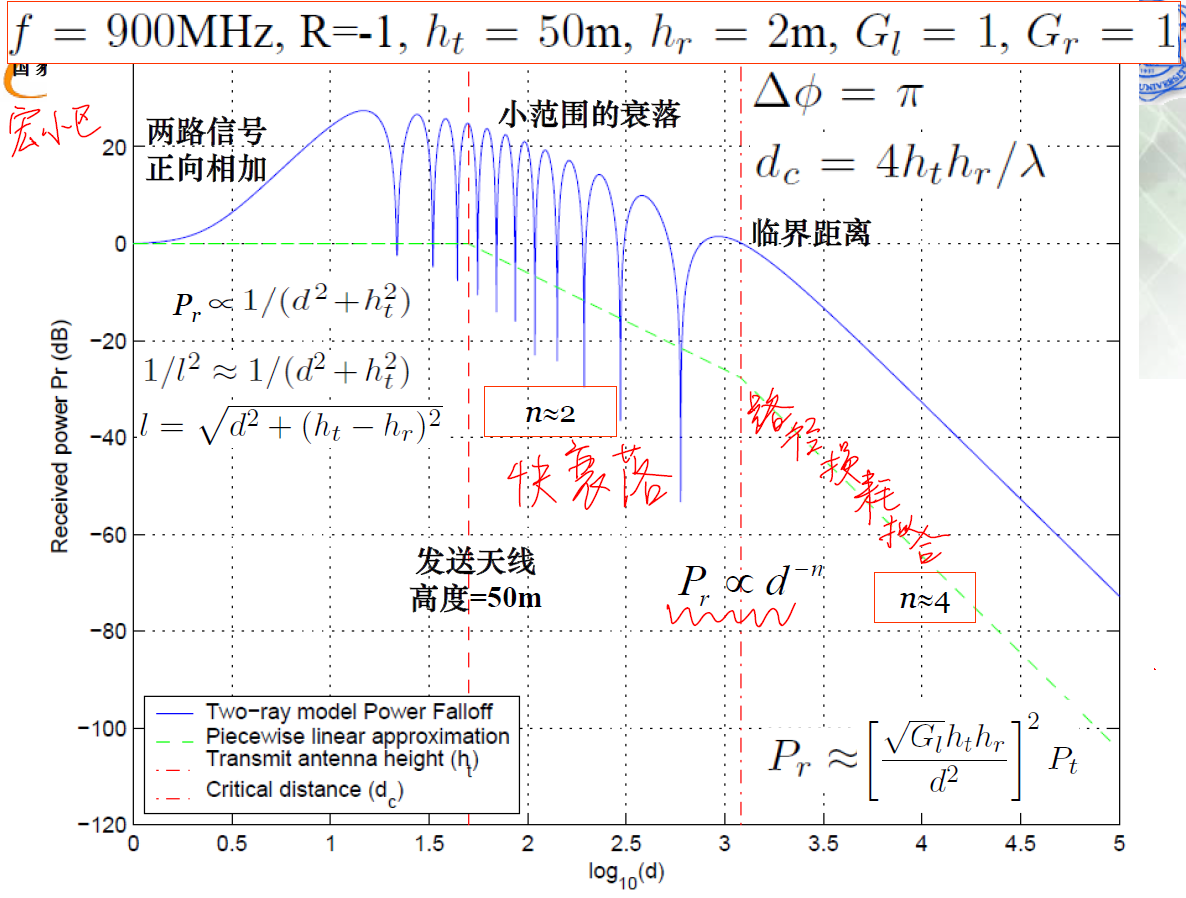
c) 典型小区半径设置
一般而言,为市区微小区典型小区半径,小区内功率衰落服从
规律,小区间干扰信号功率衰落则服从
;
为室内系统典型小区半径,但是由于穿墙损耗和多楼层穿地面/天花板损耗,实际的半径会明显小。
2.2.4、平坦衰落信道(基于随机信道分布函数的)
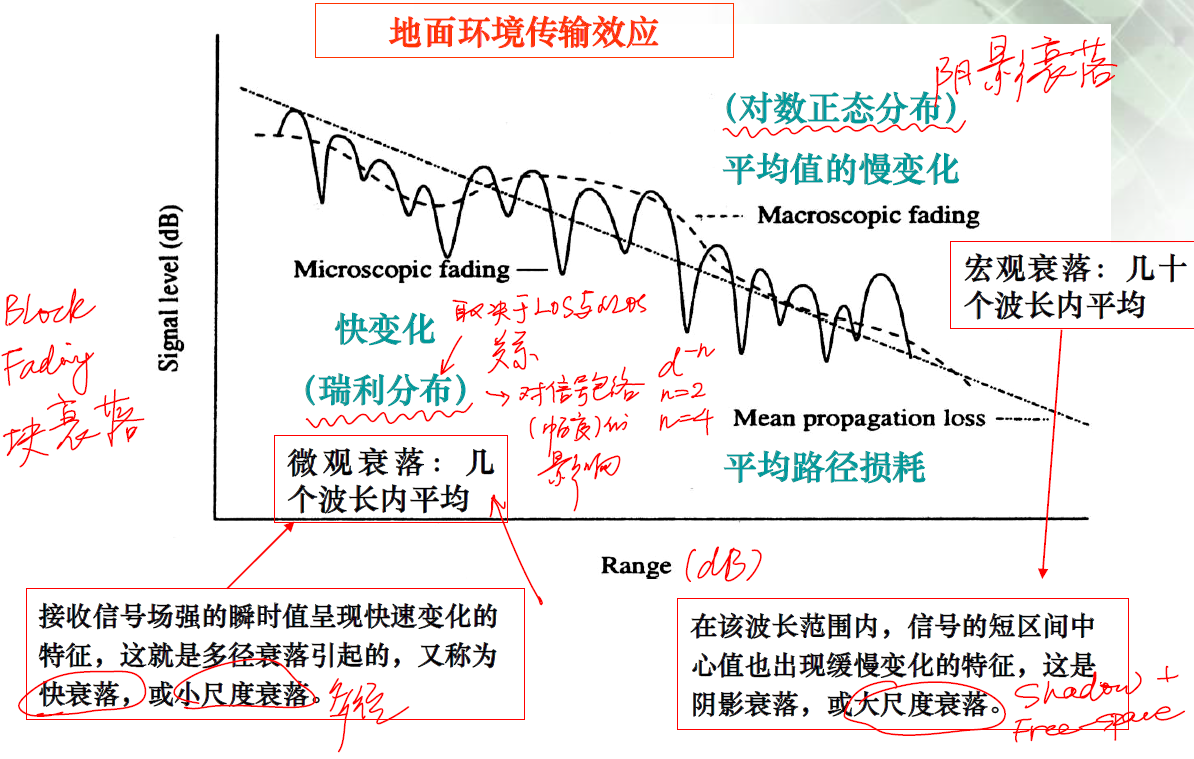
一、小尺度衰落
平坦衰落信道:无频率选择性,一段时间内分布不变的信道。
,
其中,为时变的衰落,其可以服从以下分布:
a) 当存在大量统计独立散射体且没有一个散射体占主导,服从瑞利(Rayleigh)分布:
,
它的包络幅度服从高斯分布,相位均匀分布,功率分布。
b) 当一个散射体占主导(通常视为LOS分量),服从莱斯(Rice)分布:
,
其中,A是主导地位信号幅度,是第一类零阶贝塞尔函数,
是莱斯参数。
c) 实际测量结果(更具一般性):
,
当m=1,瑞利分布;当,莱斯分布。
以上瑞利衰落和莱斯衰落被称为小尺度衰落,描述的是大约10波长内的幅度变化。
二、大尺度衰落
大尺度上,平均幅度F服从对数正态分布:
,
其中,是信号功率,
,
是ln(F)的均值和方差,其均值主要由基站和移动台之间的路径损耗决定,方差通常在4~8 dB.
2.2、传播预测模型
路径损耗预测问题(又称为信号中值预测):在给定条件(发射机天线高度、位置、工作频率、接收天线高度、收发距离、天线方向图)时,计算接收信号的场强或信号中值。
2.2.1、Hata模型
关于平均路径损耗的经验公式,适用于150M~1500MHz. Hata模型将城市地区损耗作为标准,并给出了其他地区的矫正公式。城市地区公式如下:
,
其中,是载波频率,
是发射端(基站)高度(30~200m),
是收端(移动台)高度(1m~10m),d是收发水平距离(1km~20km,宏小区),
是移动台天线矫正函数,是覆盖面积的函数。
可以看作是之前的路径损耗因子
.
对于中小城市,移动台修正因子为:
,
对于大城市,建筑物的平均高度超过15m(影响到信号的绕射),修正因子为:
2.2.2、IMT-2000室内路径损耗模型
室内办公室测试环境下的路径损耗模型:
,
R为收发距离,n为楼层间隔层数。表示路径损耗因子约为3. L在任何情况下都不应该比自由空间损耗小,可以期望 12dB 的对数正态阴影衰落标准偏差。(?)
2.2.3、其他路径损耗模型
不想看了
METIS信道模型
a) Map-based model(简化的射线追踪)
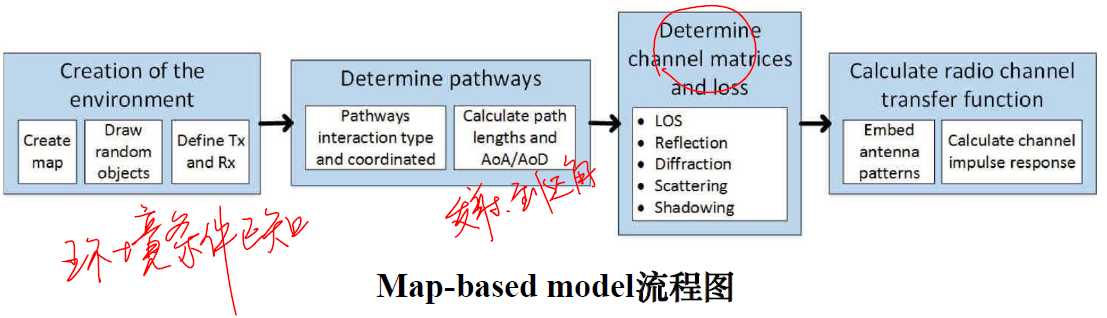
b) Geometry-based stochastic model(信道参数随机产生)
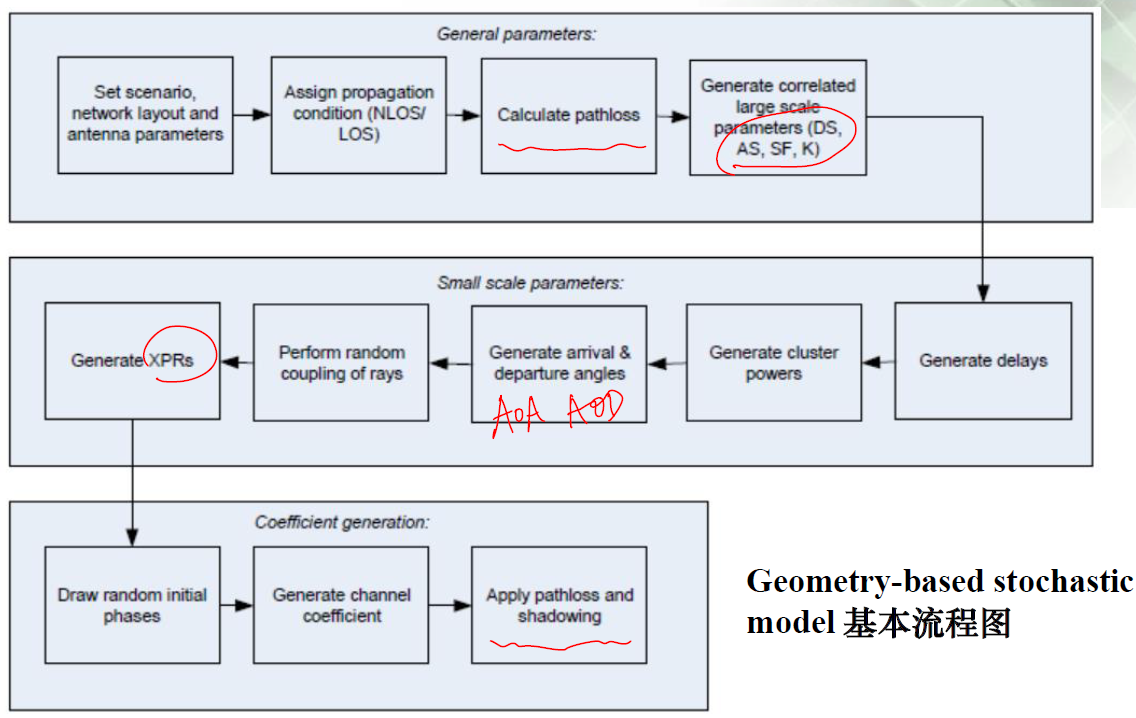
2.3、信道冲激响应

2.3.1、IMT-2000信道模型
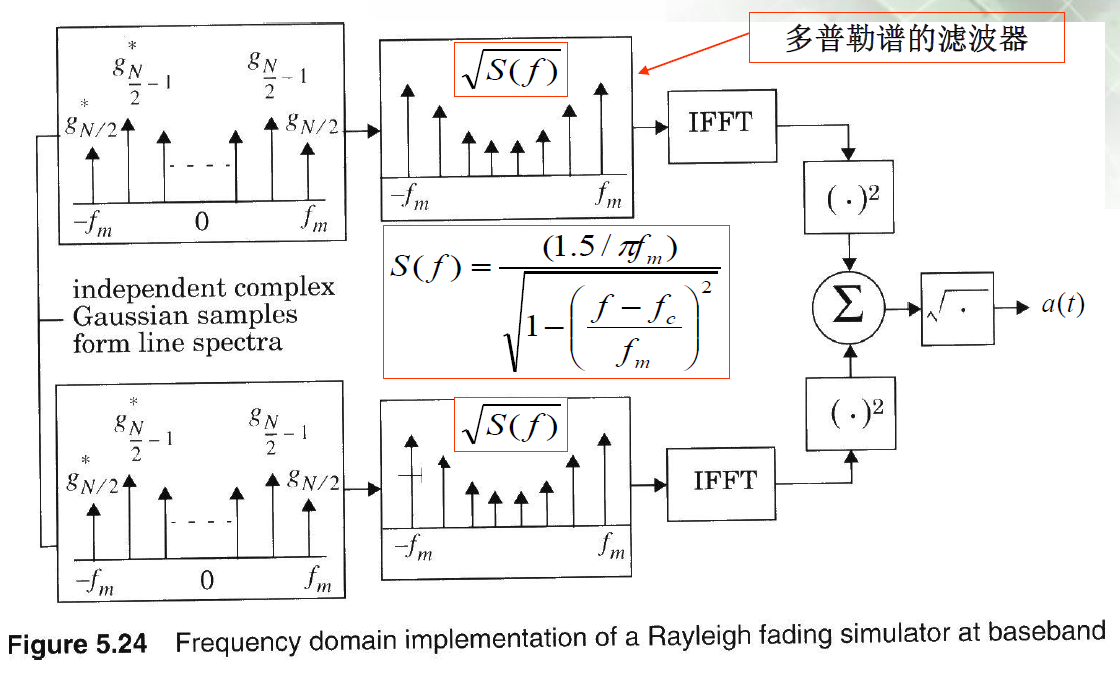
2.3.2、多普勒功率谱
a) 典型多普勒功率谱
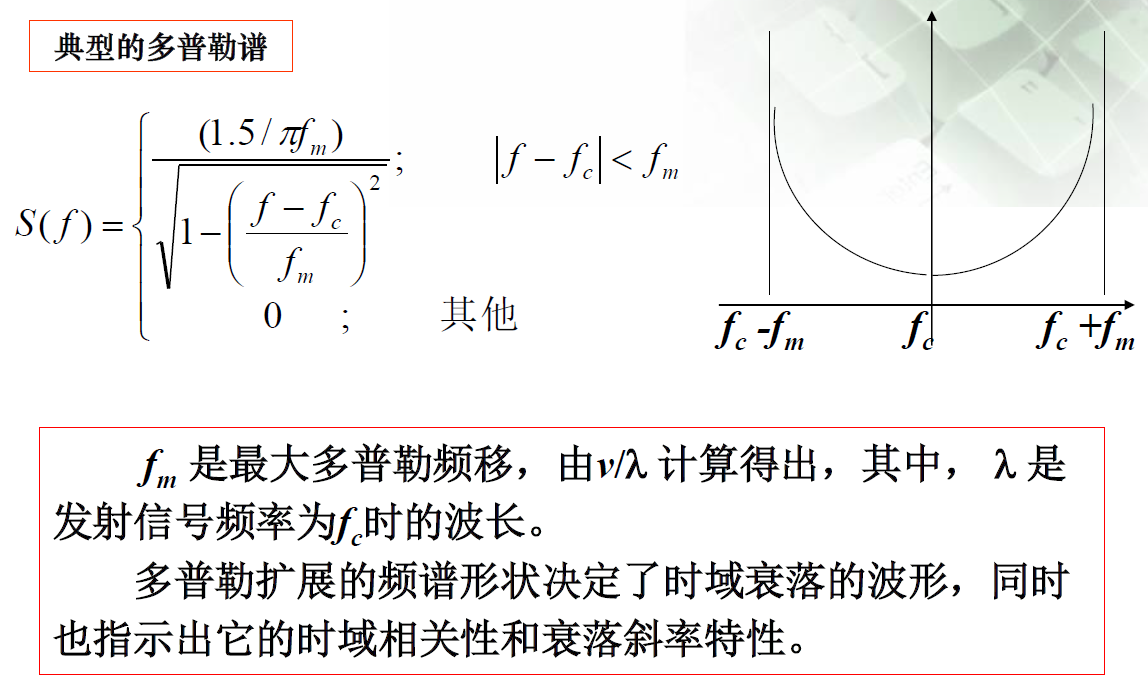
b) COST 207模型多普勒功率谱
COST 207(1989年)模型确定了功率时延谱(PDP),它分为四种情况:乡村地区(RA)、典型城市(TU)、恶劣城市地区(BU)、山地地区(HT),由以下不同种类多普勒谱加权叠加而成:
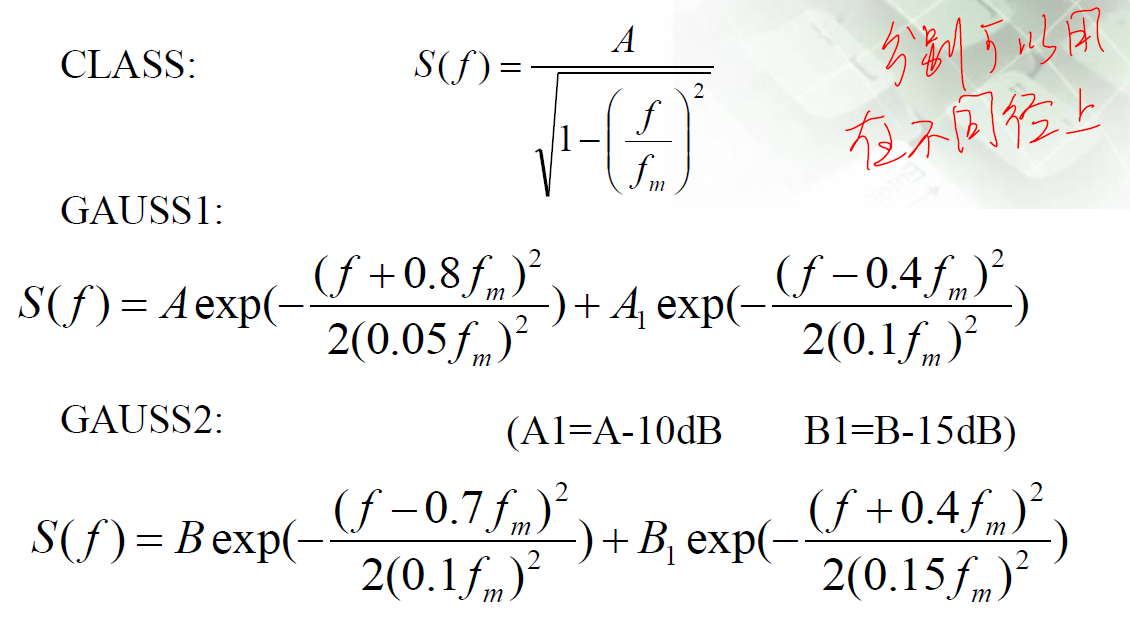
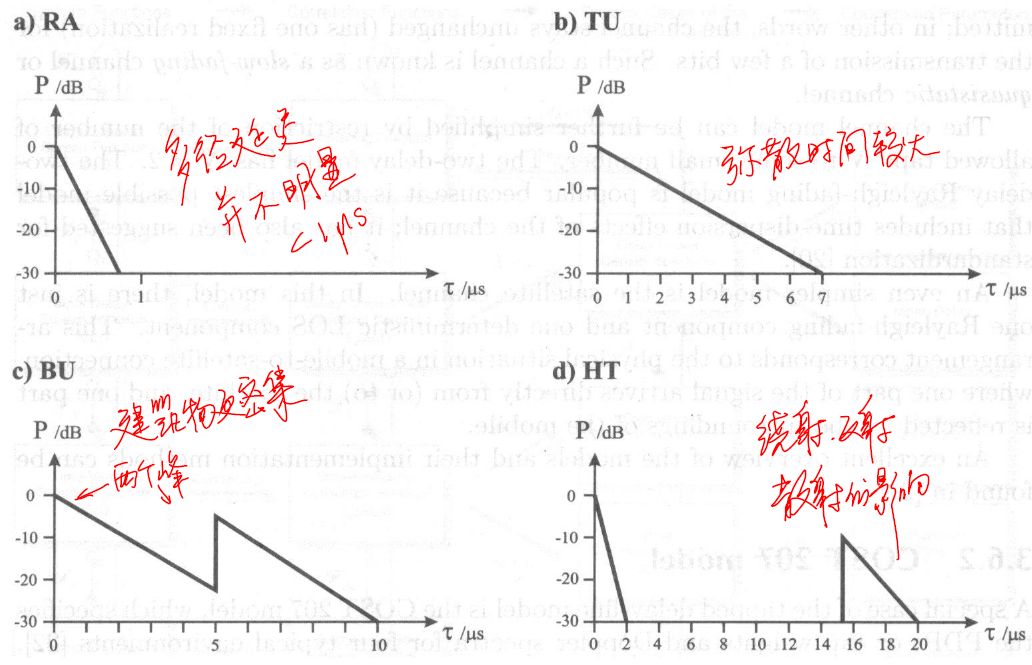
TU加权叠加:
HT加权叠加:
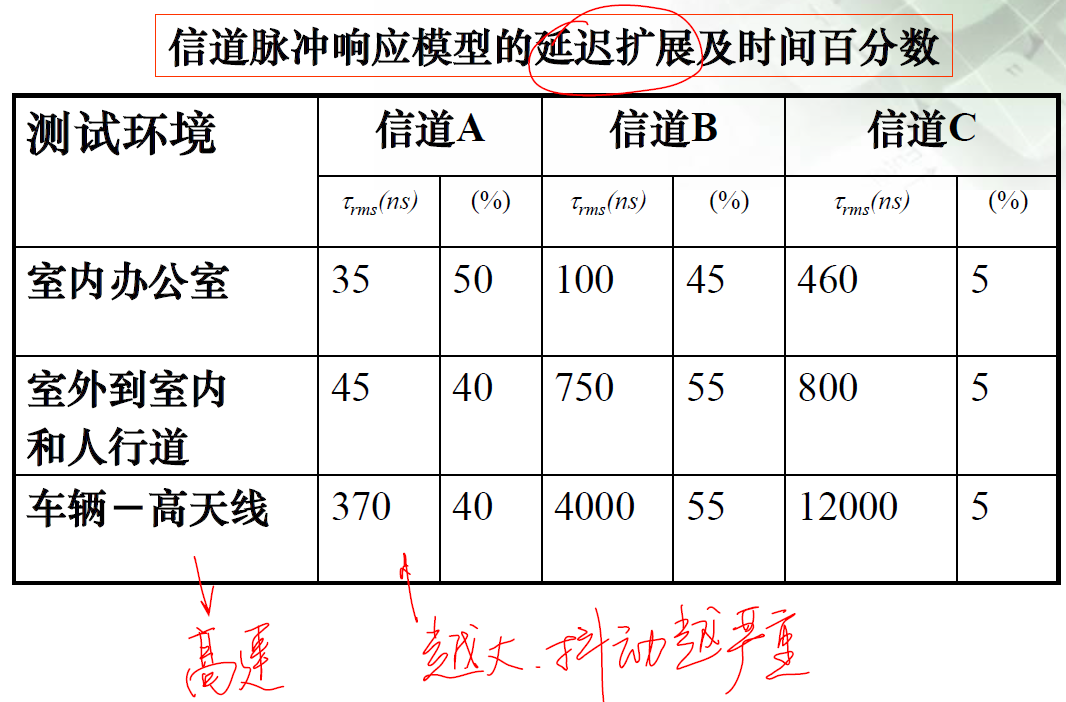
2.3.3、多径时延主要参数
a) 平均时延
.
b) RMS时延拓展(均方根)
,
表征功率的弥散程度。
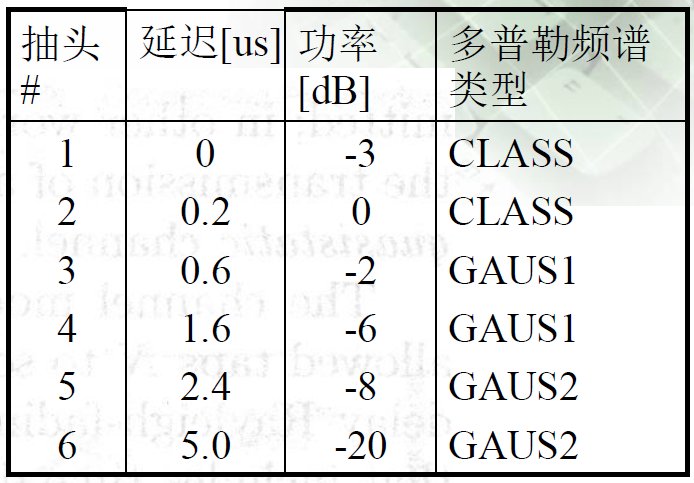
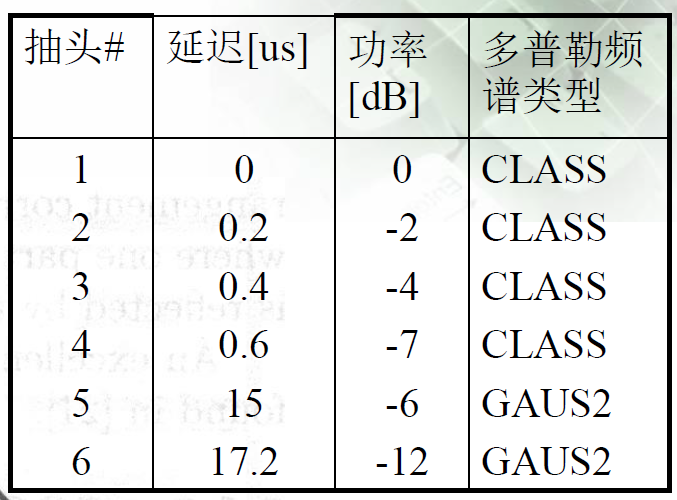
c) IMT-2000信道模型典型参数
2.4、信道响应理论模型
包括:a) 多径产生的电平快衰落和时延 扩展;
b) 多普勒频移产生的随机调频。
2.4.1、冲激响应
线性时变信道:
,
为信道的冲激响应,是二维随机过程,描述该过程的参数有时延,多普勒频移,反射系数等。
多径环境下,冲激函数可以表示为:
,
其中,N表示多径数目,是每个多径的幅值(衰减系数),
是多径时延(相对时延差),
是多径相位。
2.4.2、扩展函数和时变传输函数
确定性信道还可以用下列任一系统函数表示:
a) 时变传输函数(time-varying transfer function)
,
将时延d 影响平均掉,看时间对信道的影响。
b) 多普勒时延扩展函数(delay-Doppler spread function, 简称信道扩展函数)
.
a) b) 二者关系:
.
c) 输出多普勒扩展函数
,
时间和时延都平均掉,输出信号y(t)的傅里叶变换:
.
宽带系统冲激响应、扩展函数和时变传输函数例子:


2.4.3、随机模型(冲激响应的相关函数)
冲激响应的相关函数:
.
a) 广义平稳(wide sense stationary-WSS)信道
,
WSS特性:具有不同多普勒频移的信号是不相关的。
b) 不相关散射(US-uncorrelated scattering)信道
,
US特性:具有不同时延的信号是不相关的。
c) 广义平稳不相关散射(wide sense stationary with uncorrelated scattering -WSSUS)信道
.
定义功率时延谱PDF来研究WSSUS信道的参数:
.
两个间隔和
的信号之间的相关函数为
,
其中,是最高频率,
是RMS时延扩展,
是第一类零阶贝塞尔函数。
2.4.4、相干时间和相干带宽
a) 相干时间(Coherence Time)
,
注意:不是倒数!
b) 相干带宽(Coherence Bandwidth)
.
如果信号带宽大于相干带宽,则是频率选择性信道;若干信号的符号区间大于相干时间,则是时间选择性信号。
3、考虑空间特性的信道模型(方向性天线)
3.1、有到达角的信道模型
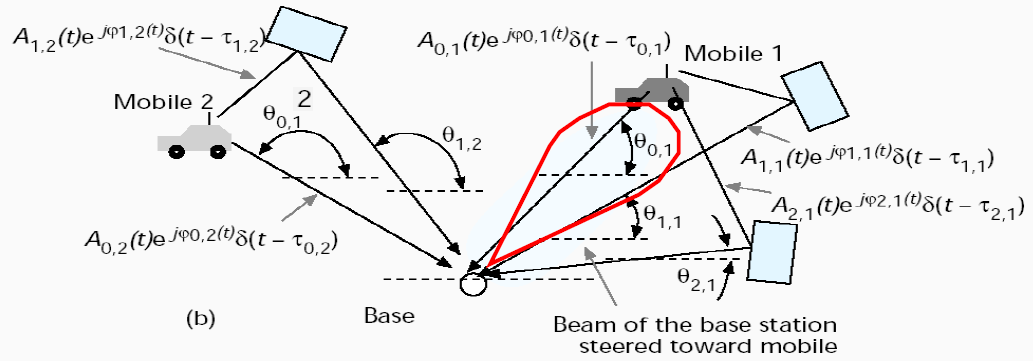
每个信号分量所经过的路径不同,第k个移动台的第 l 个信号分量由下列路径的参数确定:信号幅度 ,载波相位
,时间延迟
,多普勒频移
,到达角(AOA, Angle of arrival)
.
对于窄带信号,考虑AOA后移动台1到基站的信道冲激响应矢量如下:
,
其中,是阵列响应向量。
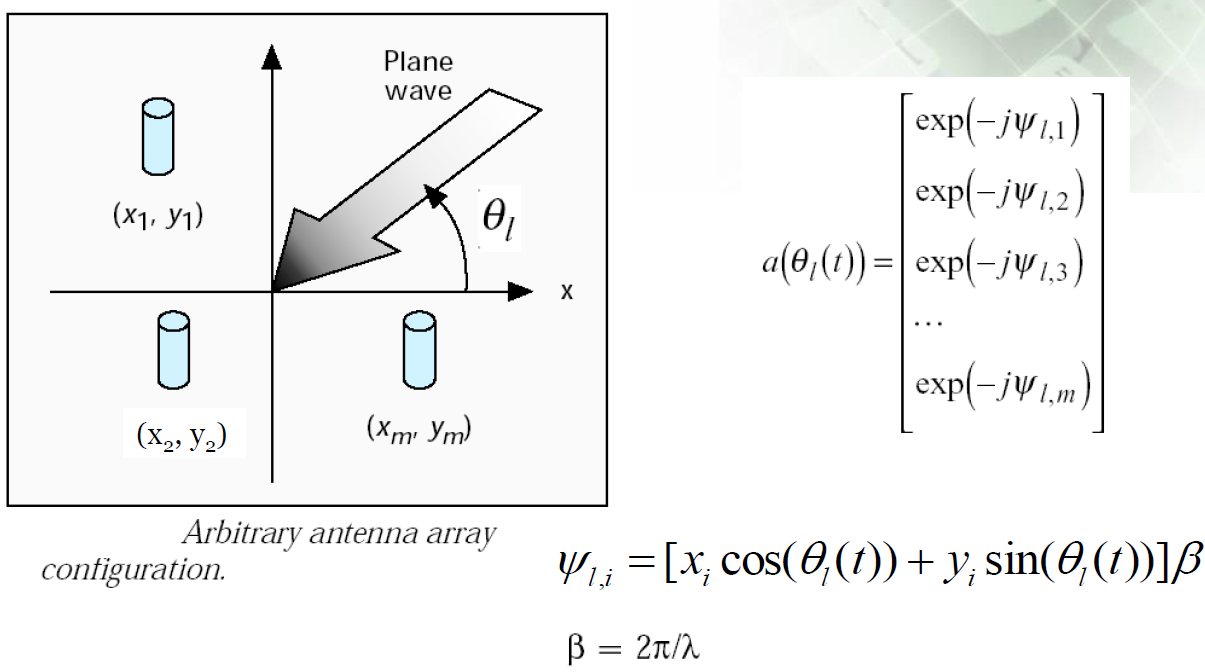
3.2、平均AOA和角度扩展
a) 平均AOA
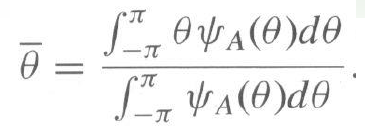
b) RMS角度扩展
表征空间选择性衰落。
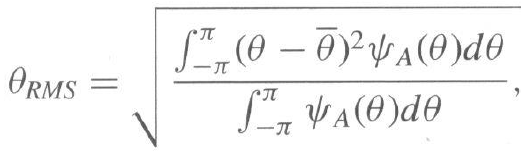
相干距离:定义为两根天线上保持强相关的最大空间距离,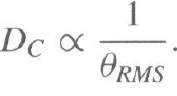
3.3、同性质信道(Homogeneous Channels)
将前文的拓展为
,即图中
.
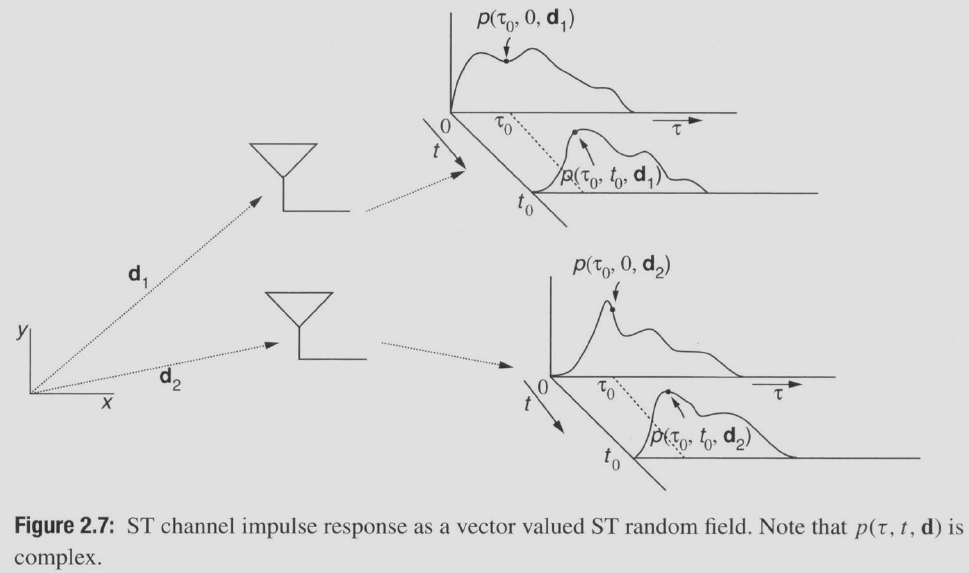
如果![]() ,则称信道在空间上局部平稳(在几十个相干距离上)或称信道是Homogeneous Channels.
,则称信道在空间上局部平稳(在几十个相干距离上)或称信道是Homogeneous Channels.
4、信道仿真模型
模拟传输(窄带):幅度+时变特性()
——>数字传输:加入时延特性
——>空间数字传输:加入空间特性(散射体空间分布、天线附近散射体的物理尺寸,散射体的数量和位置取决于天线的高度和周围环境,基站和移动台之间的差异非常重要)
4.1、宏小区基站
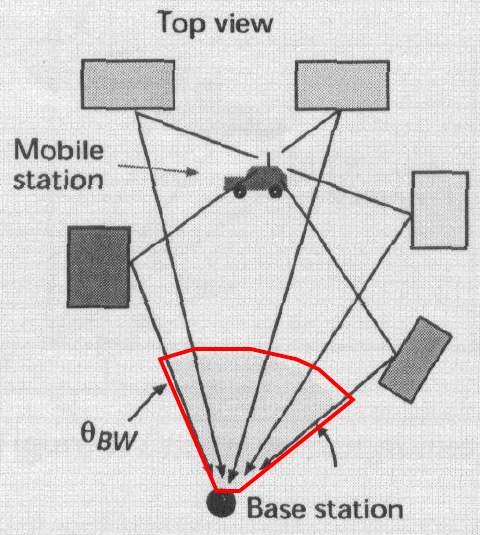
多径考虑的角度较小()。
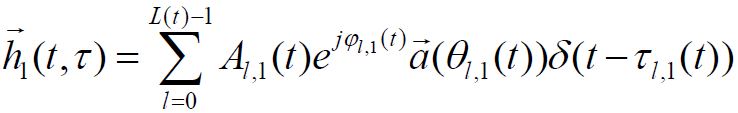
4.2、Lee模型
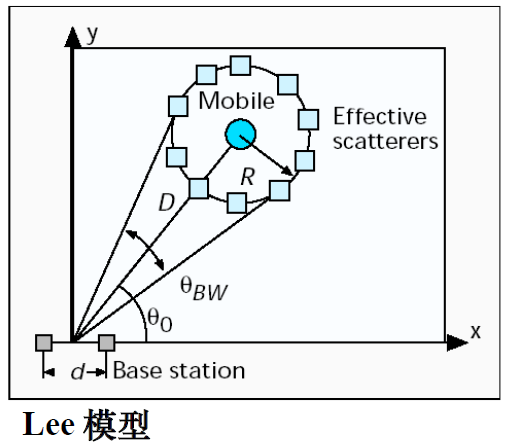
假设N个散射体均匀的分布在半径为R的圆上,并且有一个散射体在移动台和基站中间,那么离散的AOA为:
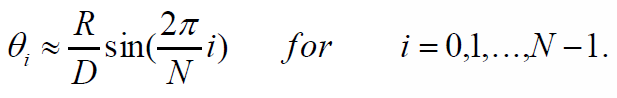
从离散AOA表达式可以得出,任意两个阵元间信号的相关表达式为:
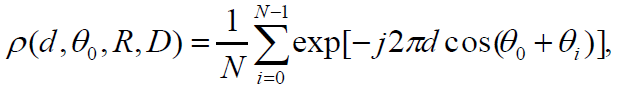
将散射体以一定的角速度运动,引入了多普勒频移。为使模型适应最大多普勒频移,散射体角速度必须等于v/R, v是移动台速度,R是散射环半径。

4.3、典型城市仿真模型
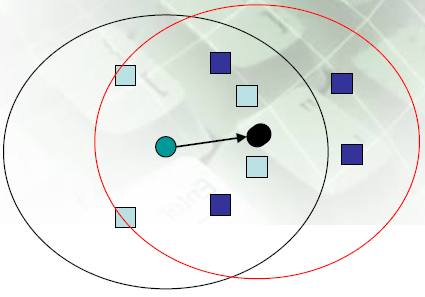
120个散射体均匀分布在半径1km的圆内。
在移动台的移动距离小于5米的时间区间内时,散射体 的位置固定不动,当移动台移动5米时,散射体回到相对于移动台的原始位置。
每个5米间隔,给散射体赋一个随机相位和随机的阴影效应(阴影效应相对于距离是对数正态分布的,有 5~10dB的标准偏差)。
4.4、恶劣城市仿真模型
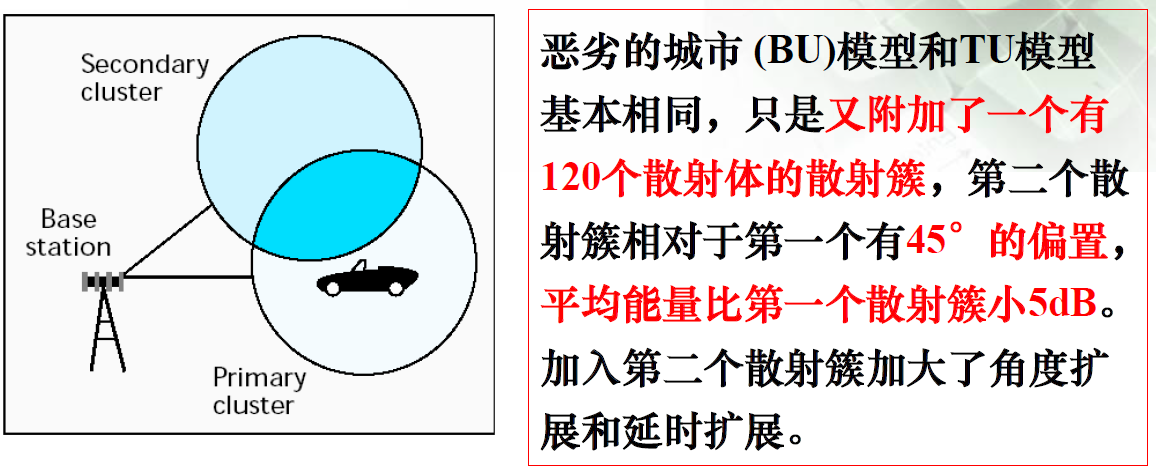
最后
以上就是高大墨镜最近收集整理的关于宽带无线通信知识点整理_第二章_信道模型1、概述2、不考虑空间特性的信道模型(全向天线)3、考虑空间特性的信道模型(方向性天线)4、信道仿真模型的全部内容,更多相关宽带无线通信知识点整理_第二章_信道模型1、概述2、不考虑空间特性内容请搜索靠谱客的其他文章。








发表评论 取消回复