对卡尔曼滤波中增益系数K表达式的理解

本人研一新生，就读于天津，第一次发帖，就把csdn当成自己的学习笔记来记录叭。
这学期开了现代信号处理这门课，大作业是写一篇review，我在学习卡尔曼滤波的过程中，查阅了大部分的博客和论文，发现很多都是介绍了卡尔曼滤波的五个核心公式，执行过程，然后举个栗子附一段代码。然而很少有相关论述说明为什么通过卡尔曼滤波算出来的结果就是最合理的。可能本人理解能力比较差，最开始只知道怎么用，研究了一段时间才明白“为什么”要这么用。
我觉得上面五个核心公式的实际意义以及每一次迭代的物理含义还是比较好理解的，其中最难理解的地方应该是增益系数K，小白在第一接触的时候，第一反应是为什么写成这个样子？为什么由K推导出的后验方差P（k|k）和后验状态X（k|k）就是合理的？

要理解这个首先需要理解卡尔曼滤波的物理意义，说的直白一些，卡尔曼滤波就是在测量结果和经验推测俩个都不准确的结论下找到则中的，最有可能接近真实值的过程。
虽然卡尔曼滤波不要求信号和噪声都是平稳过程这一假设条件，但是在使用此方法时默认测量噪声和经验估计噪声均为白噪声，即俩种获得值的方法都为高斯分布。计算增益系数K实际上就是高斯分布求积的过程。
对于俩个高斯分布：

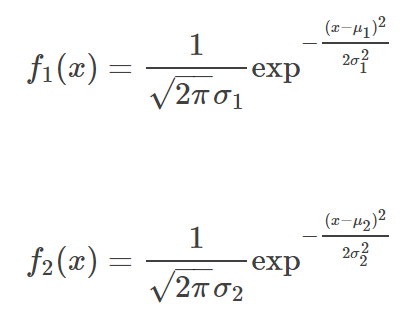
他们的乘积为：

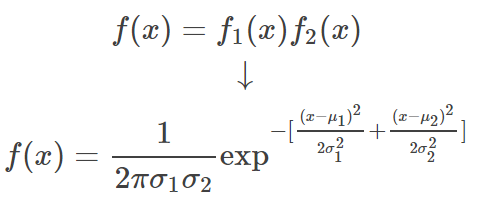
这个式子也是一个高斯分布，其分布的中心为：

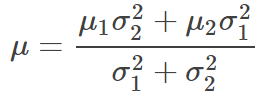
分布方差为：

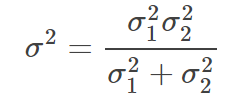
相关的推导过程百度资料有很多。对应到一元卡尔曼滤波中的增益系数K为：

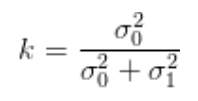
同理多元正态分布中增益矩阵K为:

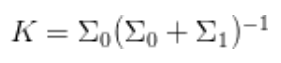
这里的K是根据多元正态分布乘积的形式推导而来的，对比卡尔曼滤波中的核心公式：

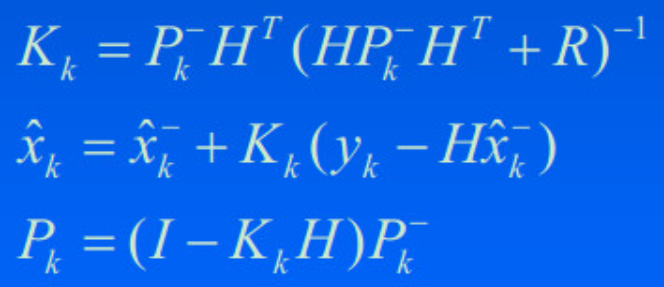
可以看出第一个式子可以理解为测量高斯分布以及经验估计高斯分布乘积的K值，第二个式子，k时刻下的后验估计和第三个式子P的后验估计相当于俩个高斯分布乘积后的新的均值和方差。而卡尔曼滤波则可以理解为此刻高斯分布乘积后的分布，与下一时刻的测量结果的高斯分布继续乘积，以这种方式估算每一个时刻下的真实值。这么理解也可以理解为什么卡尔曼滤波非常节约工作内存，因为每一个时刻的测量值都通过乘积被记录在下一时刻的后验估计值之中，也就是说，虽然某一时刻的后验估计看起来只是由前一时刻的后验估计和当前的测试值乘积得到的概率最大值，但其实通过不停地乘积和迭代这当前时刻的后验估计值已经包含了之前所有测量值所提供的参考信息的。想必这也就是卡尔曼的强大之处吧。

第一次写博客，权当学习记录，记录一下研究生期间学习过程中遇到的有意义的事情。小白一枚，哪里有写错的地方求告知，我会赶紧改正。

希望路过这儿的你可以关注我一下~~我会定期更新一系列阅读笔记和总结，加入自己的见解和思路，希望能对你有用~

最后

以上就是坚强胡萝卜为你收集整理的对卡尔曼滤波中增益系数K表达式的理解的全部内容，希望文章能够帮你解决对卡尔曼滤波中增益系数K表达式的理解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。