动态系统MATLAB分析的初步研究（一）用MATLAB进行部分分式展开用MATLAB求B（s）/A（s）的零点和极点求多项式的根动态系统数学模型的变换

63 阅读 0 评论 42 点赞

我是靠谱客的博主舒服睫毛膏，最近开发中收集的这篇文章主要介绍动态系统MATLAB分析的初步研究（一）用MATLAB进行部分分式展开用MATLAB求B（s）/A（s）的零点和极点求多项式的根动态系统数学模型的变换，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

用MATLAB进行部分分式展开

用MATLAB求B（s）/A（s）的零点和极点

求多项式的根

动态系统数学模型的变换

传递函数模型到状态空间模型的变换。

状态空间到传递函数的变换。

连续时间系统到离散时间系统的变换。

用MATLAB进行部分分式展开

现在讨论函数（一般形式）

已知传递函数：

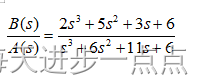
对该函数，可以通过下列命令求得其部分分式展开

>> num=[2 5 3 6]

num =

     2     5     3     6

>> den=[1 6 11 6]

den =

     1     6    11     6

>> [r,p,k]=residue(num,den)

r =

   -6.0000
   -4.0000
    3.0000


p =

   -3.0000
   -2.0000
   -1.0000


k =

     2

可以看出，留数由向量r给出，极点位置由向量p给出，直接项则由向量k给出。上述结果的部分分式展开式为：

命令residue还能用来根据部分分式展开式构成(分子和分母)多项式。即上述过程的反过程。

假设我们知道函数的部分分式展开和（如上图所示），如何求出原先的传递函数？

r = [-6	-4	3];
p = [-3	-2	-1];
k = 2;
 
>> [num,den] = residue(r,p,k)

num =

     2     5     3     6


den =

     1     6    11     6

再借助printsys()函数直接构造成传递函数（采用s的多项式的比来显示num/den）；

>> printsys(num,den,'s')
 
num/den = 
 
   2 s^3 + 5 s^2 + 3 s + 6
   -----------------------
    s^3 + 6 s^2 + 11 s + 6

对于有重极点的情况：

处理方法相同：

代码如下：

>> num=[1 2 3]

num =

     1     2     3

>> den=[1 3 3 1]

den =

     1     3     3     1

>>  [r,p,k]=residue(num,den)

r =

    1.0000
    0.0000
    2.0000


p =

   -1.0000
   -1.0000
   -1.0000


k =

     []

有重根时从前往后分别对应的是（s+1）、（s+1）^2、(s+1)^3……

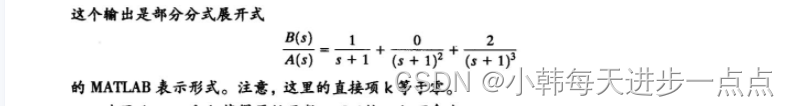
用MATLAB求B（s）/A（s）的零点和极点

MATLAB命令

[z,p,K] = tf2zp(num,den)

可以求得B(s)/A(s)的零点、极点和增益K0

同样以这个例子为例：

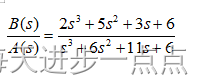
>> num=[2 5 3 6]

num =

     2     5     3     6

>> den=[1 6 11 6]

den =

     1     6    11     6

>> [z,p,K] = tf2zp(num,den)

z =

  -2.3965 + 0.0000i
  -0.0518 + 1.1177i
  -0.0518 - 1.1177i


p =

   -3.0000
   -2.0000
   -1.0000


K =

     2

可以求得该模型有一对共轭零点和一个实数零点，有三个负实部的极点（实数），系统稳定。增益K=2。

参考MATLAB帮助文档：

>> help tf2zp
tf2zp Transfer function to zero-pole conversion.
[Z,P,K] = tf2zp(NUM,DEN) finds the zeros, poles, and gains:

(s-z1)(s-z2)...(s-zn)
H(s) = K ---------------------
(s-p1)(s-p2)...(s-pn)

可见，求得的增益K为系统的根轨迹增益（即传递函数化为s的首一多项式）。

同时，可以用zplane（z，p）绘出零、极点分布图

>> zplane(z,p)

如图所示：

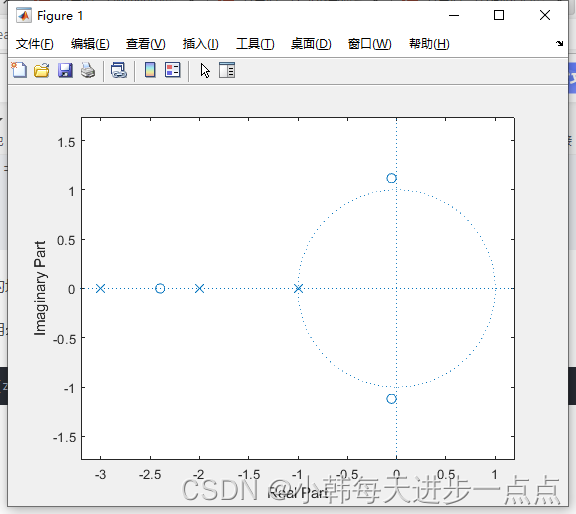
前文中提到，[z,p,K] = tf2zp(num,den)中的2谐音‘to’，表示‘到’。以此类推，[num,den]=zp2tf(z,p,k)的功能是根据零极点、增益求出传递函数B（s）/A（s）。

>> z = [-1; -2; -3];
p= [-2+j*3;-2-j*3;-5];
K = 5;
[num,den] = zp2tf(z,p,K)

num =

     5    30    55    30


den =

     1     9    33    65

>> printsys(num,den,'s1')
 
num/den = 
 
   5 s1^3 + 30 s1^2 + 55 s1 + 30
   -----------------------------
     s1^3 + 9 s1^2 + 33 s1 + 65

求多项式的根

如果只需求出零点或者极点，即只需求出多项式的根，可以采用r=roots(d)

>> d=[1 9 33 65]

d =

     1     9    33    65

>> r=roots(d)

r =

 -5.000000000000002 + 0.000000000000000i
 -1.999999999999999 + 3.000000000000000i
 -1.999999999999999 - 3.000000000000000i

上述命令即求s1^3 + 9 s1^2 + 33 s1 + 65=0的根。

命令poly(r)可以生产原来的多项式

>> d=poly(r)

d =

   1.000000000000000   8.999999999999998  32.999999999999986  64.999999999999986

动态系统数学模型的变换

MATLAB具有将线性时不变系统的一种数学模型变换为另一种模型的有用命令。下面所列的变换是在求解控制工程问题时有用的线性系统变换：

•传递函数模型到状态空间模型的变换(tf2ss)

•状态空间模型到传递函数横型的变换(ss2tf)

•状态空间模型到零点-极点模型的变换(ss2zp)

•零点-极点模型到状态空间模型的变换(zp2ss)

•传递函数模型到零点-极点模型的变换(tf2zp)

•零点-极点模型到传递函数模型的变换(zp2tf)

•连续时间系统到离散时间系统的变换(c2d)

下文先讨论传递函数模型到状态空间模型的变换。

传递函数模型到状态空间模型的变换。

命令

[A,B,C,D] = tf2ss(num,den)

将具有传递函数形式

$frac{Y(s)}{U(s)}=frac{num}{den}=C(sI-A)^{-1}B+D$

的系统变换为状态空间形式

x = Ax + Bu

y = Cx + Du

特别需要注意的是，任何系统的状态空间表达式都不是唯一的。同一个系统具有许多个（实际是无限多个）状态空间表达式。MATLAB命令只给出这些表达式中的一种可能形式。

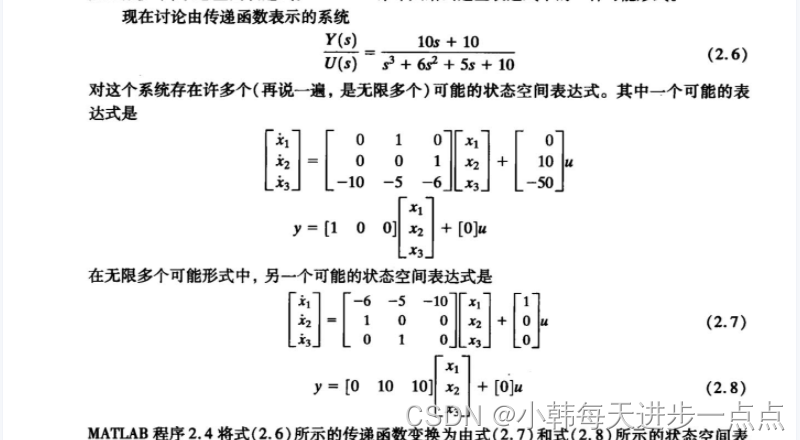
即这个系统存在着无限多个可能的状态空间表达式。下面是相应的程序：（MATLAB系统只给出一种可能性）

>>  num = [10 10];
den = [1 6 5 10];
 [A,B,C,D] = tf2ss(num,den)

A =

    -6    -5   -10
     1     0     0
     0     1     0


B =

     1
     0
     0


C =

     0    10    10


D =

     0

状态空间到传递函数的变换。

为了从状态空间方程获得传递函数，可以采用命令

[num,den] = ss2tf(A,B,C,D,iu)

对于输入量多于1个的系统必须指定iu。例如，如果该系统具有3个输入(“u1, u2,u3)，那么 iu必须是1,2或3,其中1表示u1, 2表示u2, 3表示u3。

如果该系统只有1个输入，那么既可以使用

[num,den] = ss2tf(A,B,C,D)

也可以使用

[num,den] = ss2tf(A,B,C,D,1)

对于这个状态空间表达式，可以求得两个传递函数（因为有两个输入）。下面是相应的程序：

>> A =	[0	1;-2 -3];
   B =	[1 0;0 1];
   C =[1 0];
   D =[0 0];
>> [num,den]=ss2tf(A,B,C,D,1)

num =

     0     1     3


den =

     1     3     2

>> [num,den]=ss2tf(A,B,C,D,2)

num =

     0     0     1


den =

     1     3     2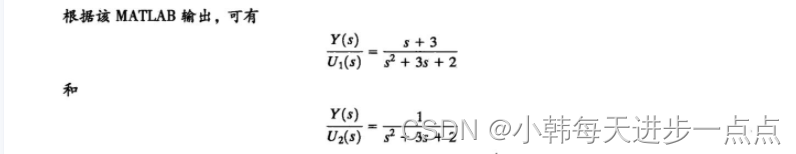

连续时间系统到离散时间系统的变换。

命令

[G,H] = c2d(A,B,Ts)

可以将连续时间状态空间模型变换为离散时间状态空间模型，其中Ts是以秒为单位表示的采样周期。这里假设输入端有个零阶保持器。也就是说，采用上述命令，能将

$dot{x} = Ax + Bu$

变换为

$x(k+1)=Gx(k)+Hu(k)$

下面是相应的程序：

>> A= [0 1;-25 -4];
>> B=[0;1];
>> [G,H]=c2d(A,B,0.05)

G =

    0.9709    0.0448
   -1.1212    0.7915


H =

    0.0012
    0.0448

值得注意的是，如果采用format long,则可以得到更加精确的H矩阵。

>> A= [0 1;-25 -4];
>> B=[0;1];
>> format long
>> [G,H]=c2d(A,B,0.05)

G =

   0.970883253819295   0.044847042382640
  -1.121176059565992   0.791495084288736


H =

   0.001164669847228
   0.044847042382640

我们发现，这两次求得的矩阵G和H是不同的，第二次求得的结果更加准确。所以，再将连续时间系统变换为离散时间系统时，建议使用format long。

我是小韩每天进步一点点，一名研0的研究生，刚开始写博客。希望和大家多多交流，一起进步！

求朋友点赞、收藏、关注哈，鼓励一下新人博主，或者提出建议。