有理假分式
所谓有理假分式,就是分子的阶数比分母高,这就导致了对有理假分式进行分式展开时必然含有直接项。
EXAMPLE

>> num = [1 8 23 35 28 3];
>> den = [1 6 8 0];
>> [r,p,k] = residue(num,den)
r =
0.3750
0.2500
0.3750
p =
-4
-2
0
k =
1 2 3
所以我们可以根据以上结果写出展开式:
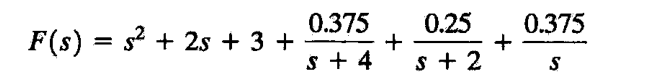
直接项
将得到的系数从右往左数,阶数从0开始依次增加。
k =
1 2 3
跟上面一样,但我们看到这个系数的时候,我们可能不知道怎么把它们跟变量的阶数配合在一起,那记住一件事情就行了,MATLAB是从低阶到高阶,所以从右往左数的话,3对应着0阶,2对应着1阶,1对应着2阶,所以直接项就是:
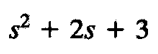
拉普拉斯逆变换
得到了展开式后,我们就可以对其进行拉普拉斯逆变换:
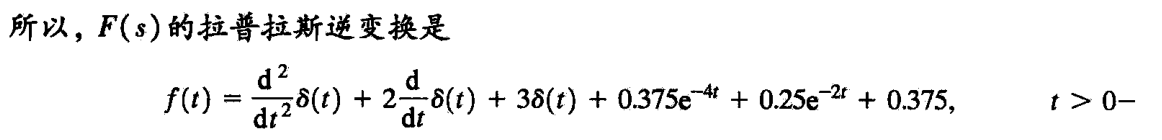
最后
以上就是顺心毛衣最近收集整理的关于三:使用MATLAB对有理假分式进行分式展开,并求取留数,极点和直接项。有理假分式EXAMPLE直接项拉普拉斯逆变换的全部内容,更多相关三:使用MATLAB对有理假分式进行分式展开内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复