一、矩阵和数组

（一）矩阵概念

在数学上，定义由$m\times n$个数$a_{ij}(i=1,2,..,m;j=1,2,..,n)$排成的$m$行$n$列的数表

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ⋮& ⋮& & ⋮\\ a_{m1}& a_{m2}& ...& a_{mn}\end{array}\right]$$
为$m$行$n$列矩阵

（二）数组概念

数组是在程序设计中，为了处理方便，把具有相同类型的若干变量按有序的形式组织起来的一种形式，这些按序排列的同类数据元素的集合称为数组
在$MATLAB$中，一个数组可以分解为多个数组元素，这些数组元素可以是基本数据类型或构造类型，因此按数组元素的类型的不同，数组又分为数值数组、字符数据、单元数组、结构数组等各种类别

（三）二者区别与联系

区别：
（1）矩阵是数学概念，数组是程序设计概念
（2）矩阵运算有明确严格的数学规则，而数组运算是MATLAB软件定义的规则，其目的是为了使数据管理方便

联系：
在MATLAB中，矩阵以数组的形式存在，因此一维数组相当于向量，二维数组相当于矩阵
所以可以将矩阵视作数组的子集

二、矩阵的构造

（一）直接赋值构造

采用矩阵构造符号——方括号“[]”，将矩阵元素置于方括号内
同行元素之间以空格或逗号隔开
行与行之间用分号“;”隔开

（二）特殊矩阵构建指令

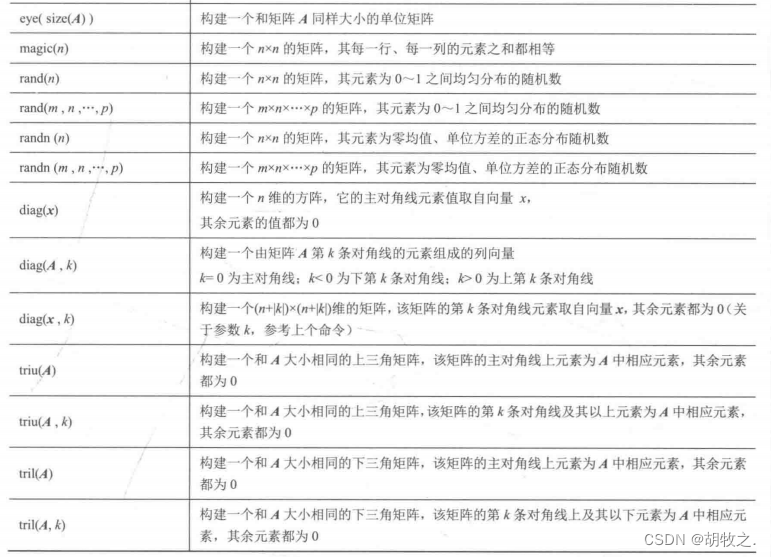
简单示例：

（三）向量、标量和空矩阵

（1）当m=1或n=1，建立的矩阵称为向量
（2）在MATLAB中，标量都是以矩阵的形式存储的，所以标量有两种表示方法
	A=[1]或者A=1
（3）当m=0或n=0时，创建的矩阵称为空矩阵，空矩阵中没有任何元素，因此不占用任何存储空间
		0矩阵只是所有元素都为0，依然占用存储空间

三、矩阵大小及结构的改变（旋转、大小改变，结构改变）

（一）B=flipdim(A,dim)，行列逆序排列

A表示一个矩阵，dim指定翻转方式。
dim为1，表示每一列进行逆序排列；
dim为2，表示每一行进行逆序排列。

（二）B=rot90(A)，逆时针旋转

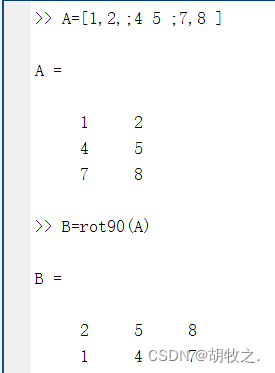
（三）B=reshape(A,m,n)，保证元素个数不变，按列不断索引

（四）B=repmat(A,[m,n])，B由m*n块A复制平铺而成

（五）B=shiftdim(A,k)，将矩阵A的维度向左移动K

当k为负值时,左移k次也就是右移-k次
假设k=1，A的维度为[1,2,3],移动后的维度就是[2,3,1]

四、矩阵下标引用

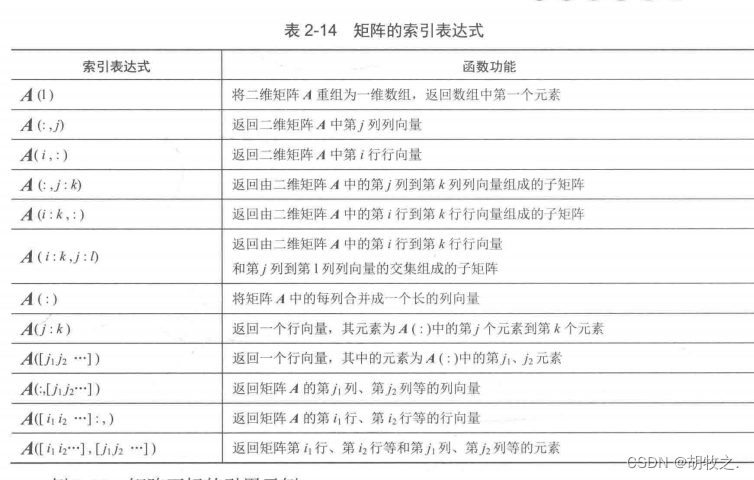
在$MATLAB$中，普通二维数组元素的数字索引分为双下标索引和单下标索引

双下标索引：A(2,3)表示矩阵A中第2行第3列的元素
单下标索引：采用列优先，对于4*4的矩阵，A(7)表示矩阵A中第3行第2列的元素

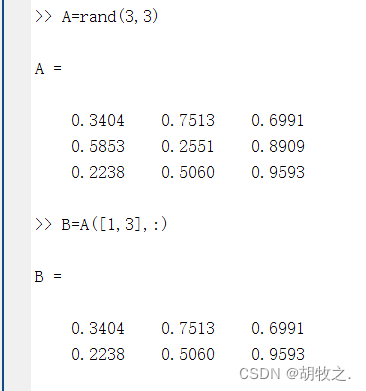
（一）访问单个矩阵元素（倒数第二行有误）

勘误：

（二）线性引用矩阵元素（如何双下标转化单下标）

（三）访问多个矩阵元素（灵活使用冒号）

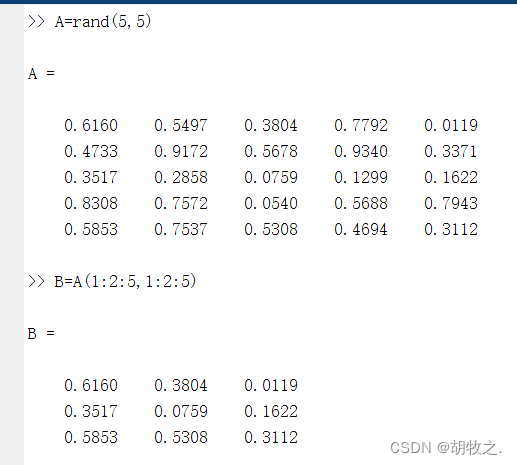
五、矩阵信息获取

（一）矩阵结构（主要判断是否为特殊矩阵）

稀疏矩阵是一种不同于一般矩阵的结构

（二）矩阵大小（维数、各维长度、元素个数）

（三）矩阵数据类型

在下方的例子中，类型依然保持了一致

六、矩阵的保存和加载

（一）矩阵存储方式

$MATLAB$中依照列优先排列的原则将元素依次放在相应的各格子里，可以通过上述的$sub2ind()$函数将双下标转换为单下标

（二）矩阵元素寻址方式

1.下标寻址

2.线性寻址（注意是列优先）

（三）矩阵元素的扩展与删除（使用圆括号）

1.扩展

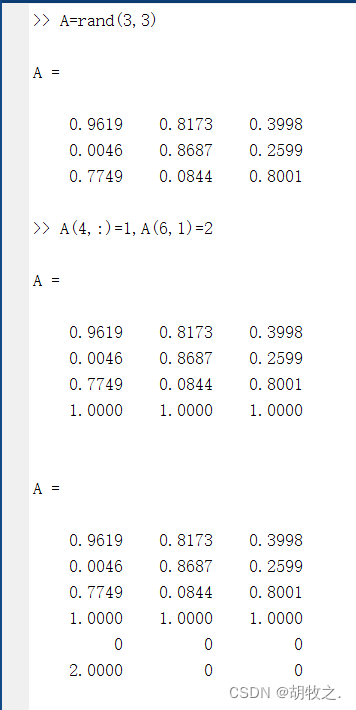
2.删除

最后

以上就是生动人生为你收集整理的MATLAB2016笔记（二）：基本矩阵操作一、矩阵和数组二、矩阵的构造三、矩阵大小及结构的改变（旋转、大小改变，结构改变）四、矩阵下标引用五、矩阵信息获取六、矩阵的保存和加载的全部内容，希望文章能够帮你解决MATLAB2016笔记（二）：基本矩阵操作一、矩阵和数组二、矩阵的构造三、矩阵大小及结构的改变（旋转、大小改变，结构改变）四、矩阵下标引用五、矩阵信息获取六、矩阵的保存和加载所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。