本次内容涉及线性代数，视频中大部分在讲解线性代数的知识，只稍微提及了几个matlab来实现的指令。
学了现代之后再来看一遍（逃~

求解线性方程

将线性方程组用矩阵 Ax=b 表示，则可通过求解矩阵来解方程：

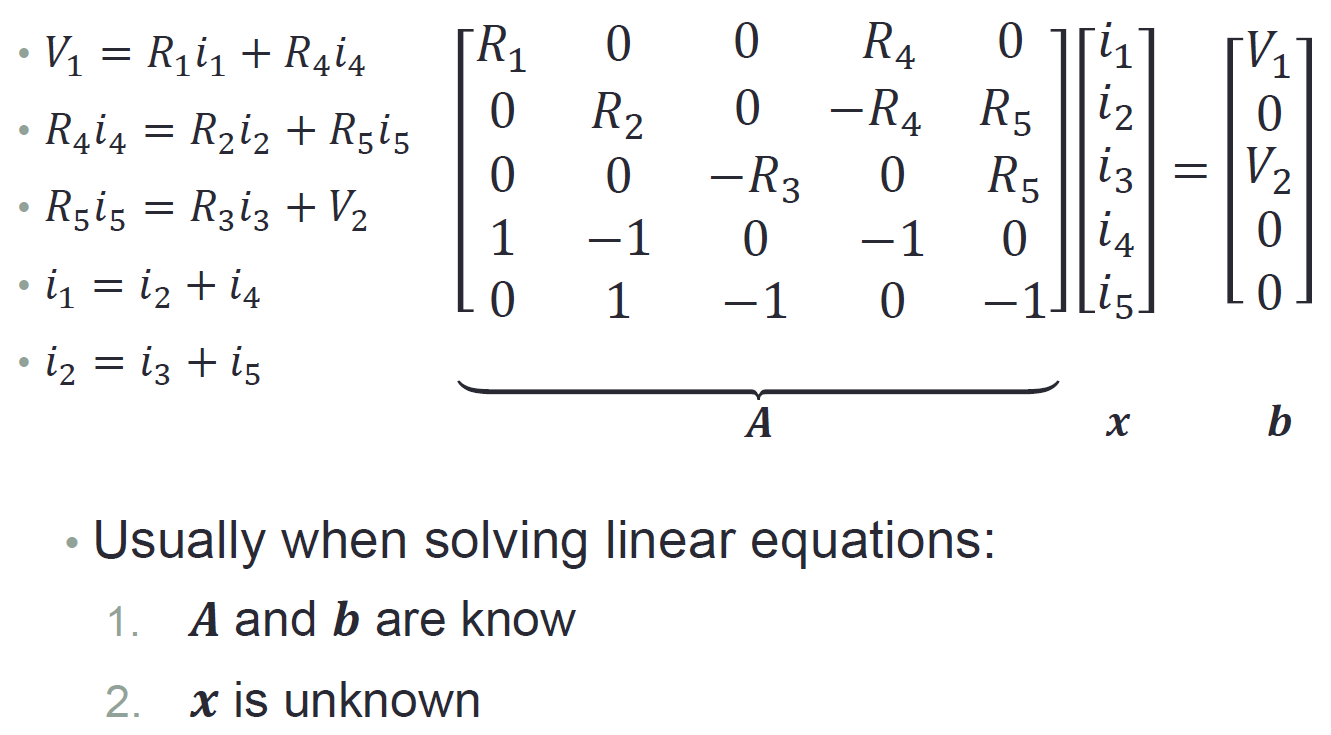
高斯消去法rref()

R = rref(A) 使用 Gauss-Jordan 消元法和部分主元消元法返回A的简化行阶梯形。
对增广矩阵 [A b] 使用rref()则可以求解 Ax=b 对应的线性方程组

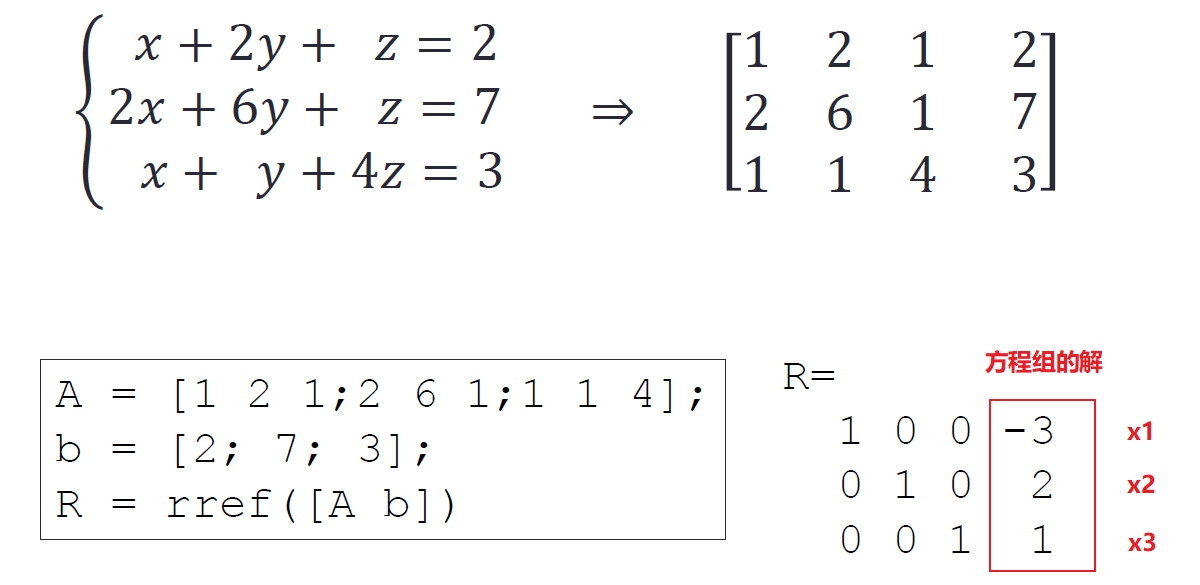
LU因子化

[L,U,P] = lu(A) 将满矩阵或稀疏矩阵 A 分解为一个上三角矩阵 U 和一个经过置换的下三角矩阵 L，使得 A = L*U；返回一个置换矩阵 P，并满足 A = P’*L*U。
通过执行 LU 分解，然后使用因子来简化问题，对线性方程组求解。

一些矩阵分解函数

• qr()：正交三角分解
• ldl()：Hermitian 不定矩阵的分块 LDL 分解
• ilu()：不完全 LU 分解
• chol()：Cholesky 分解
• gsvd()：广义奇异值分解
• svd()：奇异值分解

高效mldivide()、

以上两种方法在对于一般的线性方程组的求解其实并不友好，过于繁琐。实际上，更加高效的方式是使用Ab（或者mldivide(A,b)）可直接求得方程组的根 向量x。

克莱默法则

求解矩阵方程 Ax=b ，x等于A的逆矩阵乘以b，即 x=A^-1b
通过inv(A)对矩阵A求逆，然后直接计算即可：x = inv(A)*b

需要注意，矩阵A的逆矩阵可能不存在

线性系统

特征值和特征向量eig()

e = eig(A) 返回一个列向量，其中包含方阵 A 的特征值；
[V,D] = eig(A) 返回特征值的对角矩阵 D 和矩阵 V，其列是对应的右特征向量，使得 AV = VD。

模糊综合评价中利用eig()求解最大特征根和权向量：

矩阵指数expm()

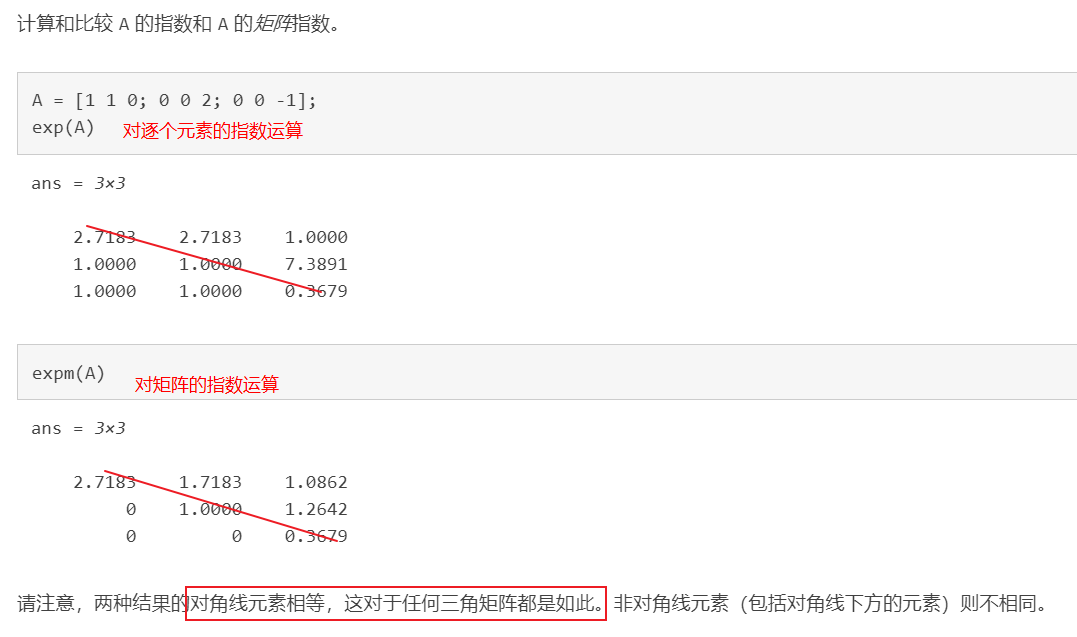
Y = expm(X) 计算 X 的矩阵指数。如果 X 有一组完整的特征向量 V 和对应特征值 D，[V,D] = eig(X)，则expm(X) = V*diag(exp(diag(D)))/V；
对于逐个元素的指数运算，使用 exp()

习题

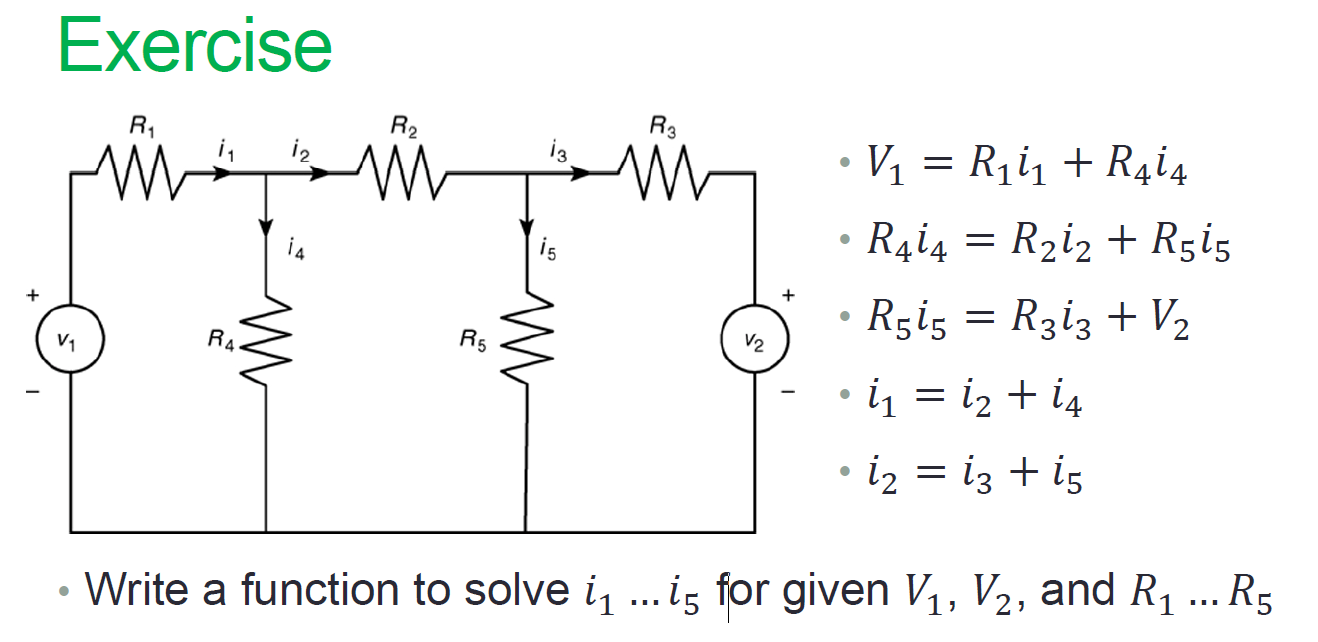
syms R1 R2 R3 R4 R5 V1 V2;
A=[R1 0 0 R4 0;0 R2 0 -R4 R5;0 0 -R3 0 R5;1 -1 0 -1 0;0 1 -1 0 -1];
b=[V1;0;V2;0;0];
x=Ab

以上内容为个人笔记，部分图片来源于郭老师课件或课程截图。
笔记汇总：MATLAB基础教程
课程视频：https://www.bilibili.com/video/BV1DA411Y7bN

最后

以上就是现实唇彩为你收集整理的MATLAB数学建模 线性方程式与线性系统求解线性方程线性系统习题的全部内容，希望文章能够帮你解决MATLAB数学建模 线性方程式与线性系统求解线性方程线性系统习题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。