matlab计算一组数的函数值_2.Matlab数值数组及其运算

2.1引导

2.2一维数组的创建与寻访

2.3二维数组的创建

2.4二维数组元素的标识

2.5二维数组的子数组寻访和赋值

2.6执行数组运算的常用函数

2.7数组运算和矩阵运算

2.8多项式的表达和创建

2.9多项式运算函数

2.10标准数组生成函数和数组操作函数

2.11数组构建技巧综合

2.12高维数组的创建

2.13关系运算

2.14逻辑操作

2.1　　引导

2.1.1

function [ output_args ] =Untitled2( input_args )

x=0:0.1:1y=x.*exp(-x)

plot(x,y,'-r'),xlabel('x'),ylabel('y'),title('y=x*exp(-x)')

grid

end

运行效果

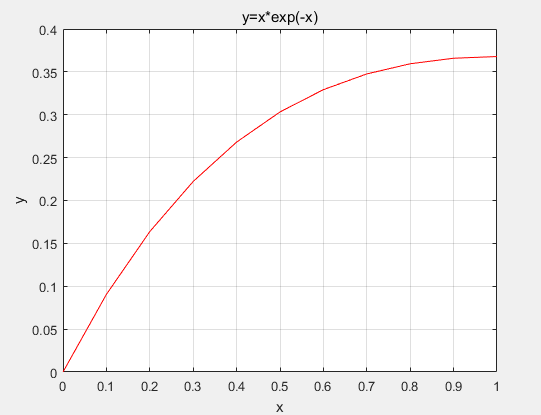
2.2　　一维数组的创建与寻访

2.2.1　　一维数组的子数组寻访和赋值

2.2.1.1　　子数组的寻访

2.2.2　　子数组的赋值

2.3　　二维数组的创建

2.3.1　　直接输入法

2.3.2　　复数数组的另一种输入方式

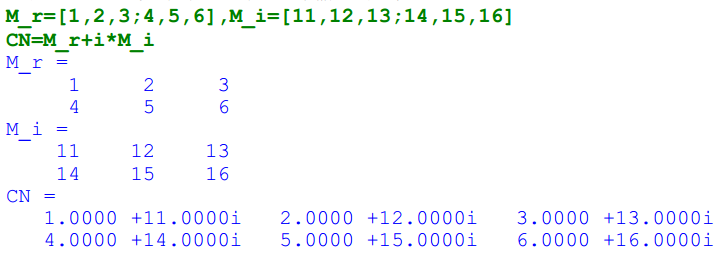
2.4　　二维数组元素的标识

2.4.1 "逻辑1"标识

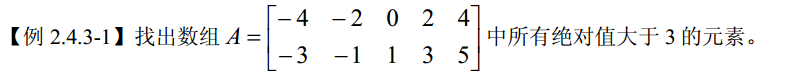
1 function [ output_args ] =Untitled2( input_args )2 A = zeros(2,5);%A 两行五列3 A(:)=-4:5 %初始化4 L=abs(A)>3%找出所有绝对值大于3的元素5 islogical(L)%判断是否是逻辑数组6 X=A(L)%把下标给x7 end

2.4.2　　逻辑数组与一般双精度数组的关系和区别

1 function [ output_args ] =Untitled2( input_args )2 A = zeros(2,5);%A 两行五列3 A(:)=-4:5 %初始化4 L=abs(A)>3%找出所有绝对值大于3的元素5 islogical(L)%判断是否是逻辑数组6 X=A(L)%把下标给x7

8 Num=[1,0,0,0,1;0,0,0,0,1];9 islogical(Num) %Num不是逻辑数组10 %Y=A(Num)%只有逻辑数组才可以这样用,所有这样错误11 end

2.5　　二维数组的子数组寻访和赋值

2.5.1　　不同赋值方式示例

1 function [ output_args ] =Untitled2( input_args )2 A=zeros(2,4)%A初始化为2行4列3 A(:)=1:8%A从1到8赋值(每列从上到下,从左到右)4

5 s=[2 3 5 6]6 A(s)%s是A的范围从上到下7 Sa=[10 20 30 76]'%'是用于赋值用8 A(s)=Sa9

10 A(:,[2,4])=ones(2)%第二列第4列都变成1

11 end

2.6　　执行数组运算的常用函数

演示pow2的数组运算性质

1 function [ output_args ] =Untitled2( input_args )2 A=[1:4;5:8]3 pow2(A)%2的A次方4 end

2.7　　数组运算和矩阵运算

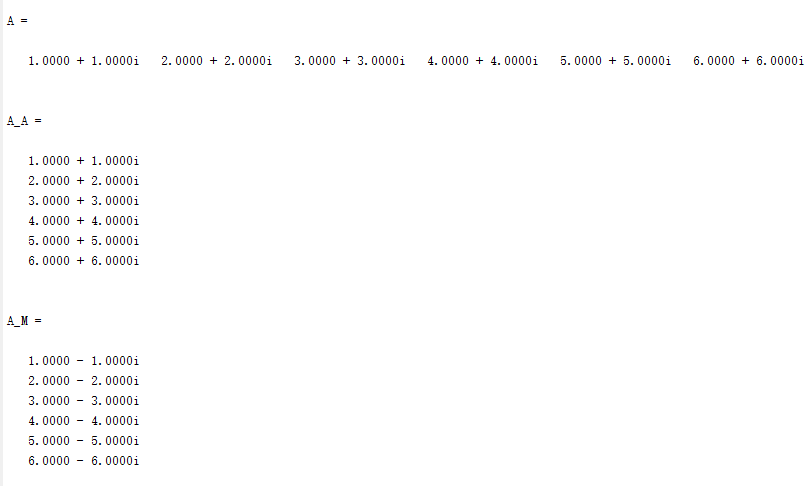
2.7.1　　两种不同转置的比较

1 function [ output_args ] =Untitled2( input_args )2 A(:)=1:6

3 A=A*(1+i)4 A_A=A.'%转置

5 A_M=A'%转置(不加.后面的复数会变号)

6 end

2.8　　多项式的表达和创建

2.8.1　　求3阶方阵A的特征多项式

1 function [ output_args ] =Untitled2( input_args )2 A=[11 12 13;14 15 16;17 18 19];3 PA = poly(A)%求特征多项式4 PPA=poly2str(PA,'s')%把特征多项式转化为表达式5 end

2.8.2　　由给定向量求多项式系数向量

1 function [ output_args ] =Untitled2( input_args )2 R=[-0.5,-0.3+0.4*i,-0.3-0.4*i]3 P=poly(R)%求特征向量4 PR=real(P)%求对应的系数向量5 PPR=poly2str(PR,'x')%转化为表达式6 end

2.9　　多项式运算函数

2.9.1

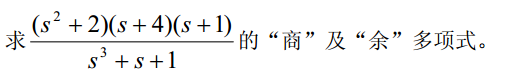
1 function [ output_args ] =Untitled2( input_args )2 %分子第一项多项式系数分别为1*s^2+0*s+2 1*s+4 1*s+1

3 p1=conv([1,0,2],conv([1,4],[1,1]));4 %分子的多项式系数 为 1*s^3 + 0*s^2 + 1*s + 1

5 p2=[1 0 1 1];6 %q,r 分别是商和余多项式7 [q,r]=deconv(p1,p2);8

9 cq='商多项式为';cr='余多项式为'

10 %转化为表达式11 disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])12 end

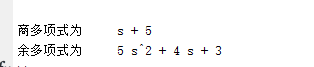
2.9.2　　polyval 与 polyvalm的区别

1 function [ output_args ] =Untitled2( input_args )2 a=[1 2 3]; %多项式为x^2+2*x+3

3 A=[1 2;3 4]; %定义一个二维矩阵4 polyvalm(a,A)%求结果

5 %其实相当于把A这个二维矩阵直接替换变量x，即求 A^2+2*A+3*E 这个矩阵多项式。6 polyval(a,A)%矩阵的每一个数都带入a运算形成一个新的矩阵7 end

2.10　　标准数组生成函数和数组操作函数

2.10.1　　标准数组的产生

1 function [A,B] = test( mark,num,array )%输入参数中，mark、num是标量，array是向量2

3 ones(1,2)4

5 ones(2)6

7 randn('state',0)8 randn(2,3)9

10 D=eye(3)11

12 diag(diag(D))13

14 repmat(D,1,3)15 end

2.10.2　　数组操作函数

diag与reshape的使用

1 function [A,B] = test( mark,num,array )%输入参数中，mark、num是标量，array是向量2

3 a=-4:4

4

5 A=reshape(a,3,3)%创建一个矩阵6

7 a1=diag(A,-1)%方向获取8

9 A1=diag(a1,-1)%方向创建矩阵10 end

数组转置.对称和旋转操作

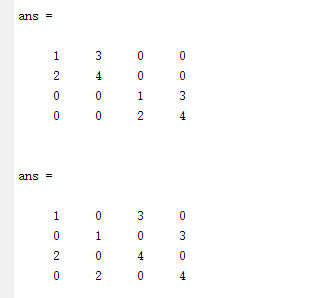
演示Kronecker乘法不具备"可交换规律"

1 B=eye(2)2 C=reshape(1:4,2,2)3

4 kron(B,C)5 kron(C,B)

2.11　　数组构建技巧综合

2.11.1　　数组的赋值扩展法

2.11.2　　多次寻访扩展法

2.11.3　　合成扩展法

2.11.4　　提取子数组,合成新数组

1 function [A,B] = test( mark,num,array )%输入参数中，mark、num是标量，array是向量2 A = reshape(1:9,3,3)%分配一个3*3的数组3 A(5,5)=111%第五行第五列设为1114 A(:,6)=222%第六列全设置为2225

6 AA=A( : ,[1:6,1:6])%拓展7

8 B=ones(2,6)%创建数组,2行6列9 AB_r=[A;B]%B作为A的后两行10 AB_c=[A,B(:,1:5)']%B的1-5列的转置 作为A的后两列

11

12 AB_BA=triu(A,1)+tril(A,-1)%对角线取反相加13

14 %AB1=[A(1:2,:);B(1,:)]%A数组的第一行第二行, B取第一行15 AB1=[A(1:2,end:-1:1);B(1,:)]%A数组的第一行第二行,从后到前颠倒 B取第一行16

17 end

2.11.5　　单下标寻访和reshape指令演示

2.11.6　　对列(或行)同加一个数 三种方法

1 clear2 A=reshape(1:9,3,3)3 b=[1 2 3]4 A_b1=A-b([1 1 1],:)%每一行按顺序减 1 2 3

5 A_b2=A-repmat(b,3,1)%b按顺序减16 A_b3=[A(:,1)-b(1),A(:,2)-b(2),A(:,3)-b(3)]%每一列减1 2 3

2.11.7　　逻辑函数的运用

2.12       高维数组的创建

function [ output_args ] =Untitled( input_args )%UNTITLED 此处显示有关此函数的摘要%此处显示详细说明

A(2,2,2)=1%第二行第二列第二层

B(2,5,:)=1:3%第二行,第五列,所有层

clear

A=ones(2,3)

A(:,:,2)=ones(2,3)*2%加了一层

A(:,:,3)=ones(2,3)*3%加一层

end

2.12.1      由函数ones zeros rand randm直接创建标准高维数组

1 rand('state',1111),rand(2,4,3)

2.12.2      借助 cat, repmat, reshape 等函数构作高维数组

1 cat(3,ones(2,3),ones(2,3)*2,ones(2,3)*3)

1 reshape(1:12,2,2,3)

2.12.3      高维数组的维数,大小和长度

1 A=reshape(1:24,2,3,4);2 dim_A=ndims(A)3 size_A=size(A)4 L_A=length(A)5 dim_A =

6 3

7 size_A =

8 2 3 4

9 L_A =

10 4

2.12.4  数组元素对称交换指令flipdim的使用示例

2.13　　关系运算

2.13.1　　关系运算示例

2.13.2　　关系操作求近似极限

1 function [ output_args ] =Untitled( input_args )2 t=-2*pi:pi/10:2*pi3

4 y=sin(t)./t5

6 tt=t+(t==0)*eps7 yy=sin(tt)./tt8

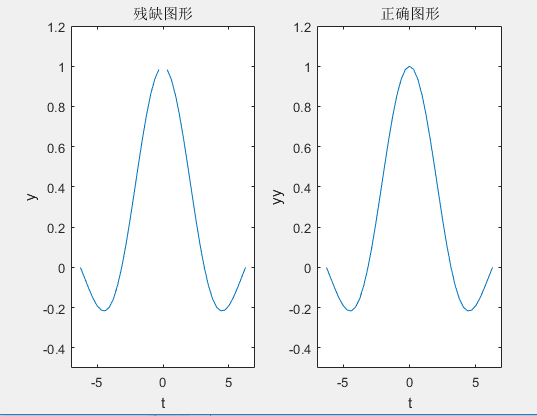
9 subplot(1,2,1)10 plot(t,y)11 axis([-7,7,-0.5,1.2])%横坐标从[-7,7] 纵坐标从[-0.5,1.2]12 xlabel('t'),ylabel('y'),title('残缺图形')13

14 subplot(1,2,2),plot(tt,yy),axis([-7,7,-0.5,1.2]),15 xlabel('t'),ylabel('yy'),title('正确图形')16 end

运行效果:

2.14　　逻辑操作

1 A=-3:3

2 L1=~(A>0)%进行判断再取反3 L2=~A>0%进行判断再取反4 L3=~A%所有都取反,非零就是15 L4=A>-2&A<1%判断是否在区间(-2,1)

2.14.1　　削顶整流正弦半波的计算和图形绘制

1 function [ output_args ] =Untitled( input_args )2 t=linspace(0,3*pi,500)3 y=sin(t)4

5 %处理方法一:6 z1=((t2*pi)).*y7

8

9 w=(t>pi/3&t<2*pi/3)+(t>7*pi/3&t<8*pi/3);10 w_n=~w;11 z2=w*sin(pi/3)+w_n.*z1;12

13

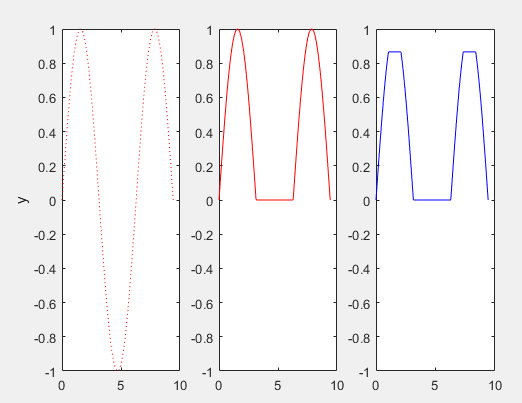
14 subplot(1,3,1),plot(t,y,':r'),ylabel('y')15 subplot(1,3,2),plot(t,z1,'r'),axis([0 10 -1 1])16 subplot(1,3,3),plot(t,z2,'-b'),axis([0 10 -1 1])17 end

运行效果

1 function [ output_args ] =Untitled( input_args )2 t=linspace(0,3*pi,500)3 y=sin(t)4

5 %处理方法二6 z=(y>=0).*y;7 a=sin(pi/3);8 z=(y>=a)*a +(y

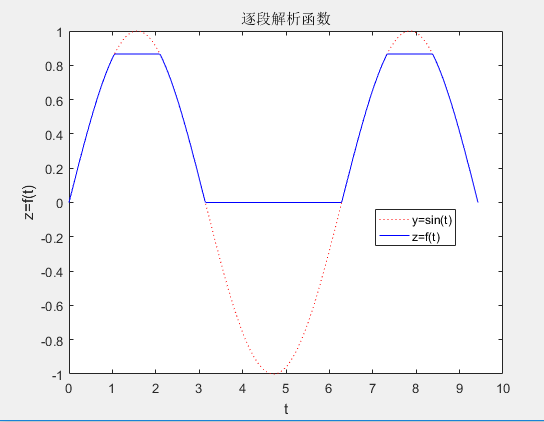
10 plot(t,y,':r')11 hold on12 plot(t,z,'-b')13 xlabel('t'),ylabel('z=f(t)'),title('逐段解析函数')14 legend('y=sin(t)','z=f(t)'),hold off15 end

运行效果