1. 前提知识 函数句柄

参考：matlab函数句柄介绍 - 百度文库

  2. 三种求sym函数的方法及其区别

function syms2vpa
%% 由符号变量生成函数，求该函数在某些点的数值
clc;clear;close all;
syms x y
z(x,y)=x.^2 + exp(y)

% x=1,y=2时 z的值
% 第一种方法：subs，输出为sym变量 
z_subs=subs(z,[x,y],[1,2])
% 第二种方法：vpa (subs )，输出为sym，且为小数点形式
z_vpa_subs=vpa(subs(z,[x,y],[1,2]))
% 第三种方法：matlabFunction，将syms函数转化为函数句柄
z_mf=matlabFunction( z )
z_mf(1,2) %输出为数值

输出：

z(x, y) =
 
x^2 + exp(y)
 
 
z_subs(x, y) =
 
exp(2) + 1
 
 
z_vpa_subs(x, y) =
 
8.389056098930650227230427460575
 

z_mf =

  包含以下值的 function_handle:

    @(x,y)exp(y)+x.^2

ans =

   8.389056098930650

 3.应用到计算傅里叶级数

% function signal_hw1_6
%% 求傅里叶级数
clc;close all;clear;
syms a t T k z
y=t.^2+z.^2;
w=2*pi/T;
x(t)=a*exp(t)
X_F=1/T*int(x*exp(-1i*k*w*t),t,-T/2,T/2) ;
% 看傅里叶级数latex形式表达式
X_F_L=sym2latex( X_F  )

% 代入数值
xf=matlabFunction(X_F)
for m=0:10
xishu1(m+1)=subs(X_F,[a,T,k],[1,2,m]);
xishu2(m+1)=vpa( subs(X_F,[a,T,k],[1,2,m]) );
xishu3(m+1)=xf(2,1,m);
end
figure;
plot([0:m],abs(xishu1) )
figure;
plot([0:m], abs(xishu2) )
figure;
plot([0:m], abs(xishu3) )

% 画出傅里叶级数柱状图
for m=0:10
absX(m+1)=abs(subs(X_F,[a,T,k],[1,2,m]));
end
k=0:10;
s=zeros([1,length(absX)]);
 
h_f=figure;
set(h_f,'Position',[100,200,600,350]);
h_p=bar(k,absX);
h_a=gca;
hold on
h_e=errorbar(k,absX,s);
 
set(h_p,'FaceColor','b','FaceAlpha',0.75,'EdgeColor','k','LineStyle','-','LineWidth',0.5)
set(h_p,'BarWidth',0.6)
set(h_e,'LineStyle','none','LineWidth',1.5,'Color','k','CapSize',8)
% set(h_a,'XLim',[-0.5,4.5],'YLim',[0,1.2])
set(h_a,'XGrid','on','YGrid','on','GridLineStyle','-','GridColor',[0.15,0.15,0.15],'GridAlpha',0.25)
xlabel('k')
ylabel('X(k)')
set(h_a,'FontName','Times New Roman','FontSize',16,'FontWeight','bold')

结果：

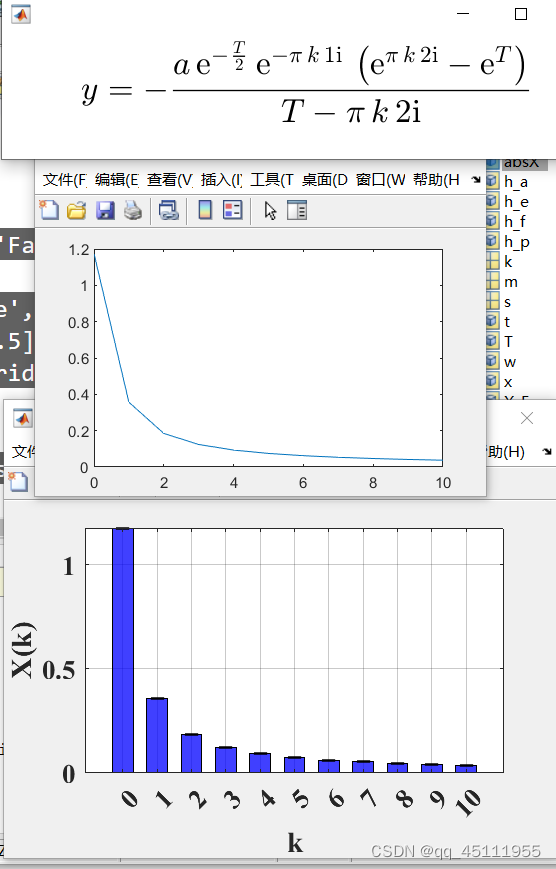
最后

以上就是缓慢小霸王为你收集整理的由syms生成函数，求该函数在某些点的数值 1. 前提知识 函数句柄  2. 三种求sym函数的方法及其区别 3.应用到计算傅里叶级数的全部内容，希望文章能够帮你解决由syms生成函数，求该函数在某些点的数值 1. 前提知识 函数句柄  2. 三种求sym函数的方法及其区别 3.应用到计算傅里叶级数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。