matlab极点配置四个极点,系统稳定性分析 、利用MATLAB 实现极点配置、设计状态观测器...

实验报告

实验名称系统稳定性分析、利用MATLAB实现极点配置、设计状态观测器系专业班

姓名学号授课老师

预定时间实验时间实验台号

一、目的要求

掌握系统稳定性的概念。学会使用MATLAB确定线性定常系统和非线性定常系统的稳定性。

掌握状态反馈和输出反馈的概念及性质。

掌握利用状态反馈进行极点配置的方法。学会用MATLAB求解状态反馈矩阵。

掌握状态观测器的设计方法。学会用MATLAB设计状态观测器。

熟悉分离定理，学会设计带有状态观测器的状态反馈系统。

二、原理简述

函数eig()的调用格式为V=eig(A)返回方阵A的特征值。

函数roots()的调用格式为roots(den)，其中den为多项式的系数行向量。计算多项式方程的解。

函数pole()的调用格式为pole(G)，其中G为系统的LTI对象。计算系统传递函数的极点。

函数zpkdata()的调用格式为[z,p,k]=zpkdata(G,’v’)，其中G为系统LTI对象。返回系统的零点、极点和增益。

函数pzmap()的调用格式为pzmap(G)，其中G为LTI对象。绘制系统的零点和极点。

对于线性定常连续系统x Ax，若A是非奇异矩阵，则原点是其唯一的平衡状态。统在原点处大范围渐近稳定的充分条件是：存在李氏函数v(x)x T px，且v(x)正定，v(x)负定。

如果SISO线性定常系统完全能控，则可通过适当的状态反馈,将闭环系统极点配置到

任意期望的位置。

MATLAB提供的函数acker()是用Ackermann公式求解状态反馈阵K。

MATLAB提供的函数place()也可求出状态反馈阵K。

如果线性定常系统完全能观测，则可构造全维(基本)观测器。全维(基本)

状态观测器的状态方程为观测器的反馈矩阵L为

其中为系统的能观测矩阵。

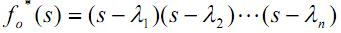
其中为期望的状态观测器的极点。观测器设计是极点配置的对偶问题，故可利用函数acker()和place()进行求解。