2-4离散的傅里叶变换
现在将之前的公式应用于离散的傅里叶级数中。
在信号处理中,遇到的常常不是一个函数,而是一个离散的数列。
下面对取值范围进行改造,首先,得到的数字信号只能在正的时间段取值,在负的时间段不能取值,但由于取的是无限长的周期序列,周期为2l,因此,把取值范围(-l,l)修改为(0,2l),这样就可以避免在负的时间段取值。
由于处理的是离散的数据序列,因此不能进行积分,而应用积分的离散形式,用求和来表示,即,在(0,2l)里等间隔取N个取值点,取样间隔为
,其中
。
可以得到
离散形式为:
其中,
,
,在实际数据处理中,k一般取N/2,此时波的周期最小,获得的频率范围最大,所以想要获得高频率的信号,就需要缩短取样间隔。
MATLAB提供了dftmtx函数来获得一个复数傅里叶变换矩阵,用法为a = dftmtx(x)
例1.计算序列x(n)的DFT
clear all
t = linspace(1e-3,100e-3,10);
xn = sin(100*2*pi*t);
N = length(xn);
WNnk = dftmtx(N);
Xk = xn*WNnk;
subplot(121);
stem(1:N,xn);
subplot(122);
stem(1:N,abs(Xk));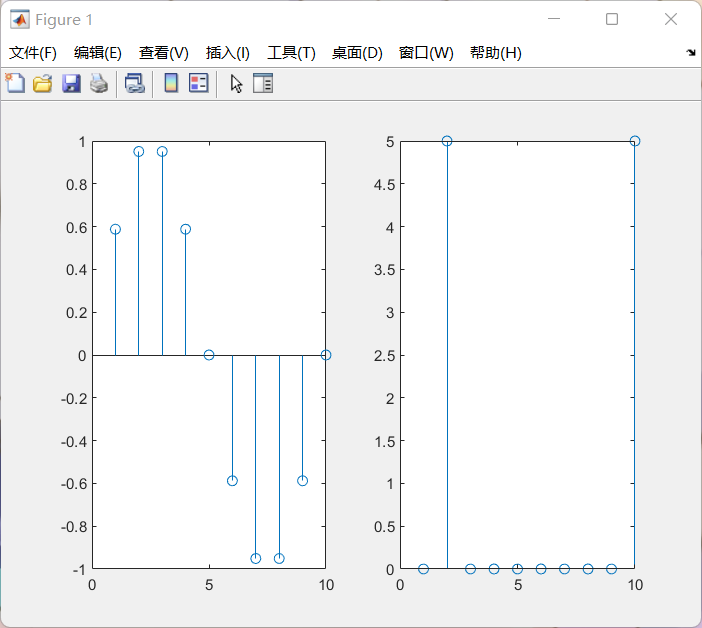
关于离散傅里叶变换的性质可以看看这个大佬的讲解,很细致
https://blog.csdn.net/SanyHo/article/details/107102323
参考资料——《MATLAB信号处理》沈再阳
matlab帮助文档
最后
以上就是老实夏天最近收集整理的关于MATLAB信号处理——信号的变换(4)2-4离散的傅里叶变换的全部内容,更多相关MATLAB信号处理——信号内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。





![matlab iir滤波器参数,[Matlab]IIR滤波器参数](https://www.shuijiaxian.com/files_image/reation/bcimg5.png)


发表评论 取消回复