MATLAB信号处理---学习小案例(4)---信号的基本运算

160 阅读 0 评论 106 点赞

我是靠谱客的博主诚心灯泡，最近开发中收集的这篇文章主要介绍MATLAB信号处理---学习小案例(4)---信号的基本运算，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

序列相加与相乘

相加
信号相加的表达式：
$x(n) = x_1(n) + x_2(n)$
```
 clear all;
 n1 = 0:3;
 x1 = [2 0.5 0.9 1];
 subplot(311);
 stem(n1,x1);
 axis([-1 9 0 2.1]);
 n2 = 0:7;
 x2 = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7];
 subplot(312);
 stem(n2,x2)
 axis([-1 9 0 0.9]);
 n = 0:7;
 x1 = [x1 zeros(1,8 - length(n1))];
 x2 = [zeros(1,8 - length(n2)) x2];
 x = x1 + x2;
 subplot(313);
 stem(n,x);
 axis([-1 9 0 2.1]);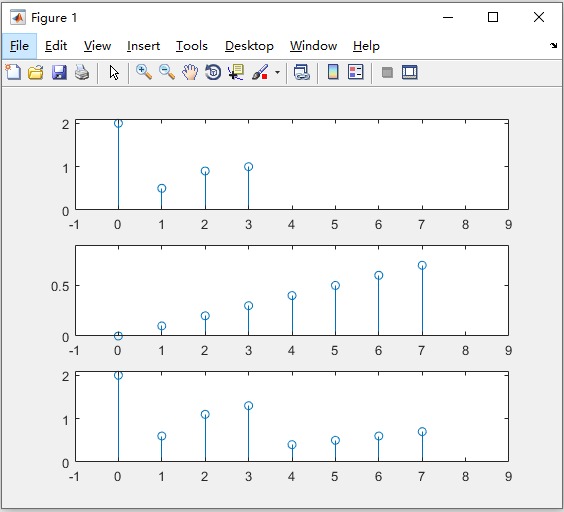
```
相乘
信号相乘的表达式，即两个序列的乘积(或称"点乘")，表达式为：
$x(n) = x_1(n) * x_2(n)$
```
 clear all;
 n1 = 0:3;
 x1 = [3 0.6 0.8 1];
 subplot(311);
 stem(n1,x1);
 axis([-1 8 0 2.1]);
 n2 = 0:7;
 x2 = [0 0.2 0.2 0.3 0.5 0.5 0.6 0.9];
 subplot(312);
 stem(n2,x2);
 axis([-1 8 0 0.8]);
 n = 0:7;
 x1 = [x1 zeros(1,8 - length(n1))];
 x2 = [zeros(1,8 - length(n2)) x2];
 x = x1 .* x2;
 subplot(313);
 stem(n,x);
 axis([-1 8 0 0.35]);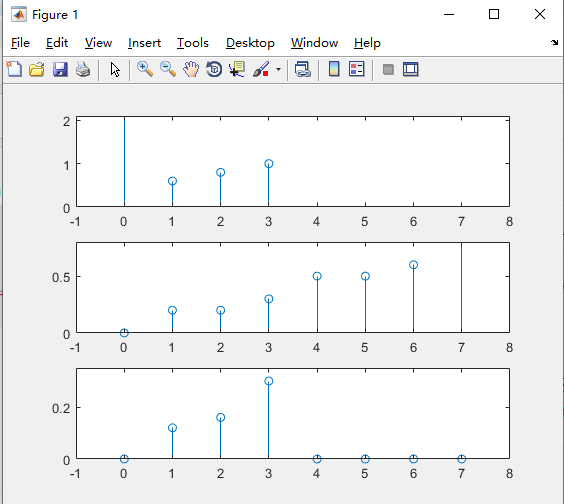
```

序列累加与序列值乘积

序列累加
序列累加式求序列x(n)两点n1和n2之间的所有序列值之和，定义如下：
$sum^{n_2}_{n=n_1}{x(n)} = x(n_1) + ……+x(n_2)$
```
 n1 = [1 2 3 4];
 sum(n1)
```
执行结果：
```
 ans =
 
     10
```
序列乘积
序列值乘积是是x(n)两点n1和n2之间的所有序列值的乘积，定义如下：
$prod^{n_2}_{n_1} = x(n_1) * ……* x(n_2)$
```
 clear all;
 x1 = [2 0.5 0.9 2 2];
 x = prod(x1)
```
执行结果：
```
 x =

 	3.6000
```

序列翻转与序列移位

序列翻转

序列翻转表达式： $y (n) = x (- n)$
```
 clear all;
 nx = -2:5;
 x = [2 3 4 5 6 7 8 9];
 ny = -fliplr(nx);
 y = fliplr(x);
 subplot(121);
 stem(nx,x,'.');
 axis([-6 6 -1 9]);
 grid on;
 xlabel('n');ylabel('x(n)');
 title('原序列');
 subplot(122);
 stem(ny,y,'.');
 axis([-6 6 -1 9]);
 grid on;
 xlabel('n');ylabel('x(n)');
 title('翻转后的序列');
 set(gcf,'color','w');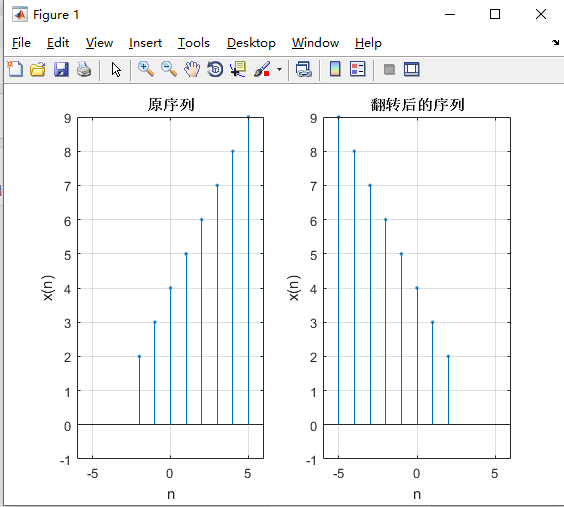
```
序列移位

序列移位表达式： $y(n)=x(n-n_0)$
```
 clear all;close all;clc;
 nx = -2:5;
 x = [9 8 7 6 5 5 5 5];
 y = x;
 ny1 = nx + 3;
 ny2 = nx - 2;
 subplot(211);
 stem(nx,x,'.');
 axis([-5 9 -1 6]);
 grid on;
 xlabel('n');
 ylabel('x(n)');
 title('原序列');
 
 subplot(223);
 stem(ny1,y,'.');
 axis([-5 9 -1 6]);
 grid on;
 xlabel('n');
 ylabel('y1(n)');
 title('右移3位后的序列');
 
 subplot(224);
 stem(ny2,y,'.');
 axis([-5 9 -1 6]);
 grid on;
 xlabel('n');
 ylabel('y2(n)');
 title('左移2位后的序列');
 set(gcf,'color','w');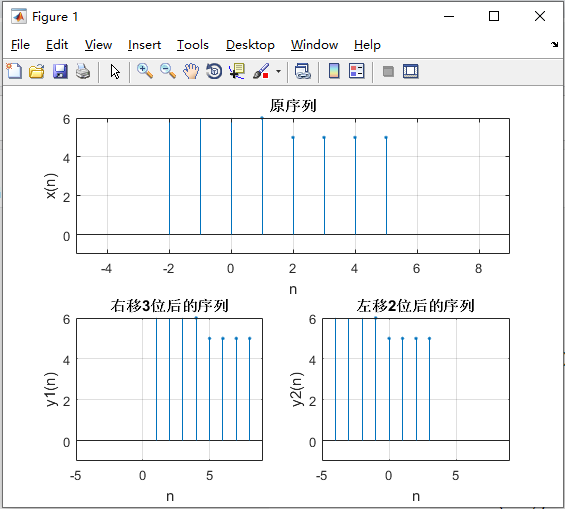
```

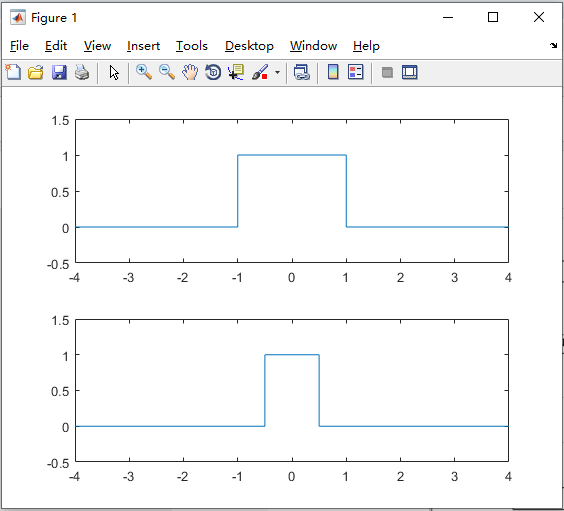
连续时间信号的尺度变换

连续时间信号的尺度变换，是指将信号的横坐标进行扩展或压缩，即将信号f(t)的自变量t更换为at，当a>1时，信号f(at)以原点为基准，沿时间轴压缩到原来的1/a；当a<1时，信号f(at)沿时间轴扩展至原来的1/a倍。

t = -4:0.001:4;
T = 2;
f = rectpuls(t,T);
ft = rectpuls(2*t,T);
subplot(2,1,1);
plot(t,f);
axis([-4 4 -0.5 1.5])
subplot(2,1,2);
plot(t,ft);
axis([-4 4 -0.5 1.5])

在这里插入图片描述
连续时间信号的奇偶分解
信号的奇偶分解原理：任何信号都可以分解为一个偶分量和一个奇分量之和的形式，因为任何信号总可以写成下式：
$f (t) = 1 / 2 [f (t) + f (t) + f (- t) - f (- t)] = 1 / 2 [f (t) + f (- t)] + 1 / 2 [f (t) - f (- t)]$
偶分量： $f_e(t)=1/2[f(t)+f(-t)]$
奇分量： $f_o(t)=1/2[f(t)-f(-t)]$

syms t;
f = sym('cos(t + 1) + t');
f1 = subs(f,t,-t);
g = 1/2 * (f + f1);
h = 1/2 * (f - f1);
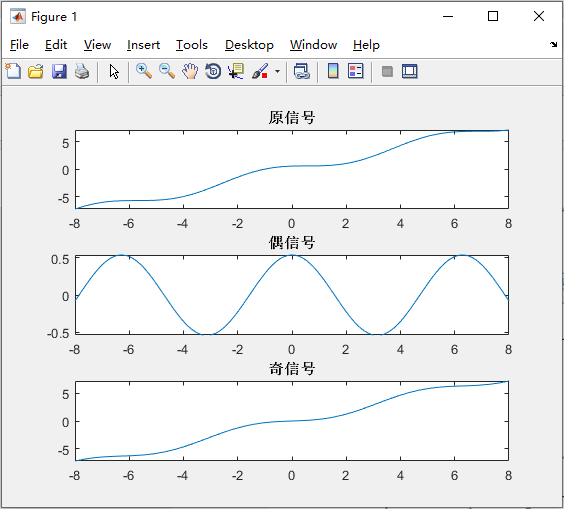
subplot(311);fplot(f,[-8,8]);title('原信号');
subplot(312);fplot(g,[-8,8]);title('偶信号');
subplot(313);fplot(h,[-8,8]);title('奇信号');

在这里插入图片描述
信号的微分和积分

微分：对于连续时间信号，其微分运算用函数diff来完成，语法格式：

 diff(function,'variable',n)

function表示的是要进行求导运算的信号，或者被赋值的符号表达式，variable为求导运算的变量，n为求导的阶数，默认值为一阶导数

 syms t f2;
 f2 = t * (2 * heaviside(t) - heaviside(t - 1)) + heaviside(t - 1);
 t = -1:0.01:2;
 subplot(121);
 ezplot(f2,t);
 title('原函数');
 grid on;
 ylabel('x(t)');
 f = diff(f2,'t',1);
 subplot(122);
 ezplot(f,t);
 title('微分函数');
 grid on;
 ylabel('x(t)');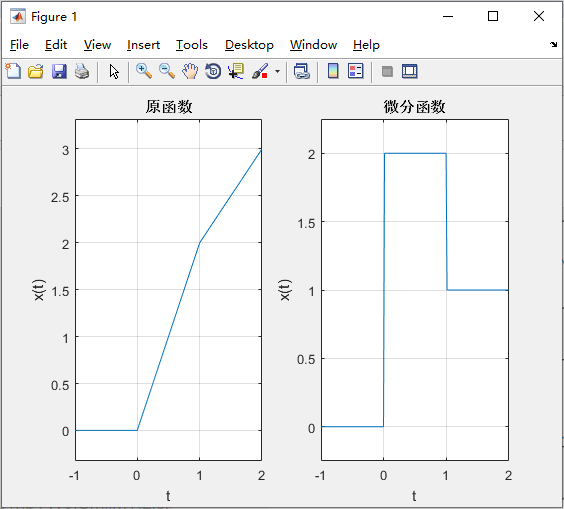

在这里插入图片描述

积分
连续信号的积分匀速那用函数int来完成，语句格式为

 int(function,'variable',a,b)

其中function表示要进行积分的信号，或者被赋值的符号表达式，variable为求导运算的独立变量，a，b为积分上、下限，a和b被省略时为求不定积分

 syms t f1;
 f1 = 2 * heaviside(t) - heaviside(t - 1);
 t = -1:0.01:2;
 subplot(121);
 ezplot(f1,t);
 title('原函数');
 grid on;
 f = int(f1,'t');
 subplot(122);
 ezplot(f,t);
 grid on;
 title('积分函数');
 ylabel('x(t)');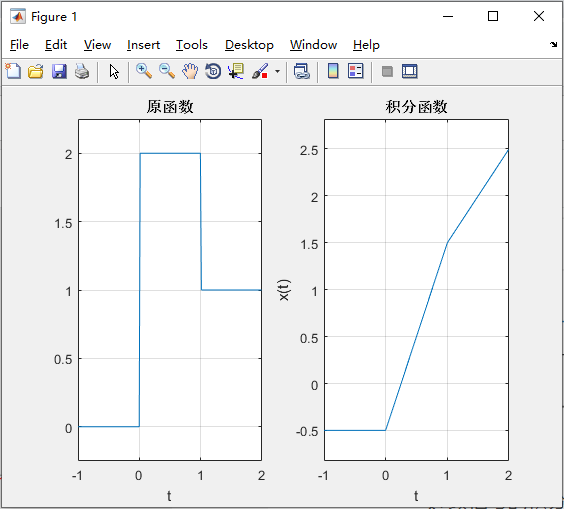

在这里插入图片描述