1 简介

      ode45，常微分方程的数值求解。MATLAB提供了求常微分方程数值解的函数。当难以求得微分方程的解析解时，可以求其数值解（解析解就是给出解的具体函数形式，从解的表达式中就可以算出任何对应值；数值解就是用数值方法求出近似解，给出一系列对应的自变量和解）。

        Matlab中求微分方程数值解的函数有七个：ode45，ode23，ode113，ode15s，ode23s，ode23t，ode23tb 。

        ode是Matlab专门用于解微分方程的功能函数。该求解器有变步长（variable-step）和定步长（fixed-step）两种类型。不同类型有着不同的求解器，其中ode45求解器属于变步长的一种，采用Runge-Kutta算法；其他采用相同算法的变步长求解器还有ode23。

        ode45表示采用四阶-五阶Runge-Kutta算法，它用4阶方法提供候选解，5阶方法控制误差，是一种自适应步长（变步长）的常微分方程数值解法，其整体截断误差为(Δx)^5。解决的是Nonstiff(非刚性)常微分方程。

2 用法

[T,Y] = ode45(odefun,tspan,y0)

odefun 是函数句柄，可以是函数文件名，匿名函数句柄或内联函数名
tspan 是区间 [t0 tf] 或者一系列散点[t0,t1,...,tf]
y0 是初始值向量
T 返回列向量的时间点
Y 返回对应T的求解列向量
————————————————
版权声明：本文为CSDN博主「Chauncey Ge」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/Loggsy/article/details/80791924

3 控制程序

控制对象电机的传递函数：

控制程序：PID_ode45.m

%增量式PID
clc % 清屏
clear all; % 删除workplace变量
close all; % 关掉显示图形窗口

ts=0.001; %采样时间
xk=zeros(2,1);
e_1=0;
u_1=0;%初始值

%%
for k=1:1:1000
    time(k)=k*ts;%时间轴，画图用
    
    yd(k)=0.5*sin(1*2*pi*k*ts);%控制目标（理想位置）
    
    %PID参数
    kp=20;
    ki=0;
    kd=0.5;
    
    para=u_1;
    tSpan=[0 ts];
    %常微分方程的数值求解，[t,y,te,ye,ie] = ode45(odefun,tspan,y0,options)
    [tt,xx]=ode45('PID_ode45_plant',tSpan,xk,[],para);
    xk=xx(length(xx),:);%xk为求解值
    y(k)=xk(1); 
    
    e(k)=yd(k)-y(k);
    de(k)=(e(k)-e_1)/ts;
    u(k)=kp*e(k)+kd*de(k); 
    
    %避免PID值饱和，限制输出
    if u(k)>10
        u(k)=10;
    end
    if u(k)<-10
        u(k)=-10;
    end
    u_1=u(k);
    e_1=e(k);  
end
    
figure(1);
plot(time,yd,'r',time,y,'k:','linewidth',2);
xlabel('时间（s）'); ylabel('yd,y');
grid on
title('仿真结果');
legend('实际信号','仿真结果');

figure(2);%误差
plot(time,yd-y,'r','linewidth',2);
xlabel('时间（s）');ylabel('误差');
grid on
title('误差');

 控制对象：PID_ode45_plant.m

function dy = PlantModel(t,y,flag,para)
u=para;
J=0.0067;B=0.1;

dy=zeros(2,1);
dy(1) = y(2);
dy(2) = -(B/J)*y(2) + (1/J)*u;

运行结果: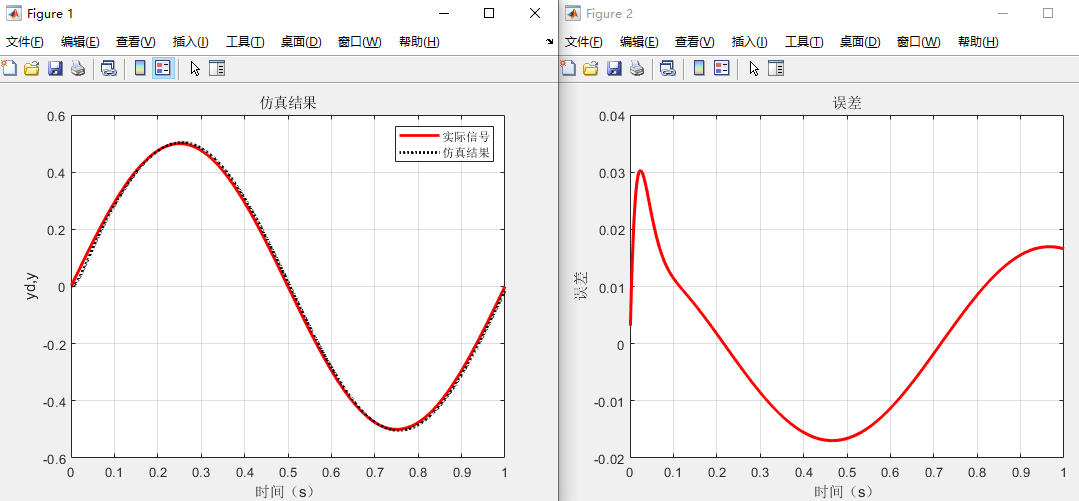

 参考材料《MATLAB_SIMULINK系统仿真》

最后

以上就是迷路月饼为你收集整理的MATLAB-基于传递函数的PID控制系统仿真1 简介2 用法3 控制程序的全部内容，希望文章能够帮你解决MATLAB-基于传递函数的PID控制系统仿真1 简介2 用法3 控制程序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。